探究初中数学中动点问题的解法

唐静 姜锐武

【摘要】初中数学中的一个教学重点和难点就是动点问题，动点问题需要学生摆脱固有思维，以运动的眼光来看待问题，另一方面，动点问题对学生的想象能力提出了较高要求.动点问题在中考中属于必考内容，而且多出现在综合性题目中，很多学生反映自己在解题过程中存在较大困难，因此，也成为一个教学难点.为了帮助学生顺利掌握解决动点问题的方法，本文以不同的动点问题进行案例分析，通过具体的解题分析，帮助学生对动点问题的解决方法进行理解和掌握，希望能给大家的教学带来启示和思考.

【关键词】初中数学;动点问题;解法

动点问题是初中数学教学的一个重要内容，动点问题的学习可以培养学生的空间想象能力和抽象思维能力，有助于提高学生的数学探究能力，对学生后续发展具有关键作用和意义.在教学过程中，教师需要引导学生根据动点的具体运动方式进行分析，结合其运动环境来寻找解题的切入点.在日常数学教学过程中，很多教师往往只是为学生简单地介绍动点的运动方式，以及相关的知识和方法，如果不与实际案例结合进行分析，学生往往无法深刻理解动点的特点以及解题关键.下面笔者就从分类的角度来阐述动点问题的解题方法.

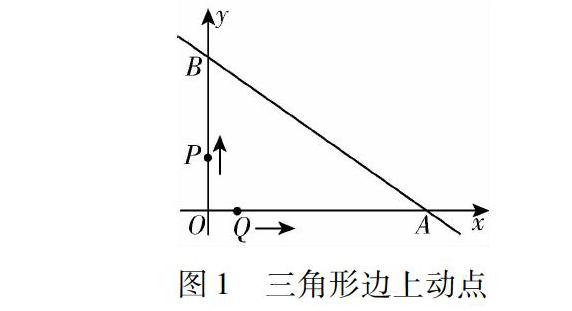
一、三角形边上动点

直线y=-34x+6与坐标轴分别交于A，B两点，动点P，Q同时从O点出发，同时到达A点，运动停止.点Q沿线段OA运动，速度为每秒1个单位长度，点P沿路线O→B→A运动.

（1）直接写出A，B两点的坐标;

（2）设点Q的运动时间为t秒，△OPQ的面积为S，求出S与t之间的函数关系式;

（3）当S=485时，求出点P的坐标，并直接写出以点O，P，Q为顶点的平行四边形的第四个顶点M的坐标.

解（1）A（8，0），B（0，6）.

（2）当0

当3

（3）M1285，245，M2-125，245，M3125，-245.

提示：第（2）问按点P到拐点B所用时间分段分类;

第（3）问是分类讨论：已知三定点O，P，Q，探究第四点构成平行四边形时按已知线段身份不同分类——① OP为边、OQ为边，② OP为边、OQ为对角线，③ OP为对角线、OQ为边.然后画出各类的图形，根据图形性质求顶点坐标.

二、特殊四边形边上动点

如图所示，菱形ABCD的边长为6厘米，∠B=60°.从初始时刻开始，点P，Q同时从A点出发，点P以1厘米/秒的速度沿A→C→B的方向运动，点Q以2厘米/秒的速度沿A→B→C→D的方向运动，当点Q运动到D点时，P，Q两点同时停止运动，设P，Q运动的时间为x秒时，△APQ与△ABC重叠部分的面积为y平方厘米（这里规定：点和线段是面积为0的三角形），解答下列问题：

（1）点P，Q从出发到相遇所用时间是秒;

（2）点P，Q从开始运动到停止的过程中，当△APQ是等边三角形时x的值是;

（3）求y与x之间的函数关系式.

提示：第（3）问按点Q到拐点B，C所用时间分段分类;提醒——高相等的两个三角形面积比等于底边的比.

三、小结

初中数学教学过程中的动点问题可以细分为几类，分别是三角形边上的点、特殊四边形边上的点、直線上的动点以及抛物线上的动点等等.不同的动点类型在具体的解题过程中需要区别对待，但是所有的动点都需要学生以运动的眼光去看待，并通过空间想象能力和抽象思维能力来模拟动点运动的过程，从而掌握动点运动的轨迹以及相关规律，在此基础上进行解题往往就能达到迅速、准确、科学的效果.

【参考文献】

[1]刘青.初中数学中一些动点问题的归类[J].数理化解题研究：初中版，2016（12）：2.

[2]巩彩红.例谈初中数学中的动点问题[J].数学学习与研究，2017（22）：144.

[3]吴晓峰.对初中数学教学中动点问题的思考[J].数学学习与研究，2017（8）：141.