核心素养视角下“二次函数应用
刘春泳
【摘要】本文注重知识融合,侧重将知识讲旧的原则,从小学算式到九年级二次函数的逐渐过渡,体现数学从特殊到一般的思想,即在学生的最近发展区设置问题,分析问题并解决问题,从而达到对核心素养的深度理解.
【关键词】核心素养;经济问题;知识融合
二次函数是初中数学的重要内容,是中考的必考考点,讲解此部分内容时,往往是讲课周期长,吸收程度差,基于此,在设计二次函数应用这一课题时,重点关注核心素养与学生无缝对接.
一、用算数激趣
问题呈现1:有三个数字2,3,5,让学生利用这三个数字写一个等式.预设学生可能会写出2+3=5,3+2=5,5-3=2,5-2=3等.
问题呈现2:根据所写的式子,赋予一定的实际意义,初步体会数学建模.
设计意图:初步体验合情推理的重要性,充分调动学生学习的积极性,也为演绎推理做积极的准备.
问题呈现3:如果把刚才的式子设置为商品买卖的问题,那么,又该如何叙述呢?
设计意图:通过开放类问法的设计,让学生能够感觉到数学来源于生活(即数学建模)这一相关知识,采用先民主后集中的方式,为二次函数的应用—经济类问题,做好积极的铺垫.
归纳总结:商品的售价-进价=利润.
为了让学生掌握新知识的效率更高,所以教师需要把新知识讲旧,这样就可以从学生的最近发展区发现问题,分析问题,从而解决问题了,效果可以达到预期,甚至超越预期.
二、用代数式提升
问题呈现4:某件商品的进价是3元,售价是x元,则:
(1)利润是多少元?
(2)如果售出商品10件,则利润又是多少呢?(以上两问均用含x的代数式表示)
设计意图:这道题是在小学算术的基础上,进行升华而成的,它体现了由数到式的一个变化过程,这个变化过程就是小学到初中的一个升华过程,也就是我们常说的数式通性,以便使学生能够体会从特殊到一般的数学思想方法.
三、用一元二次方程提升
问题呈现5:某商品的售价为x元,进价为3元,售出了2x件,利润为20元,那么商品的售价是多少呢?
设计意图:由于先前多道习题的训练,学生的思维已经达到了一定的高度,这道题学生的思考时间应该是很短的.如果还按照先前的教学模式处理,学生会形成学习惯性,不认真审题,容易出现思维定式错误法.所以,这道题首先训练学生提炼关键语句,把文字之中的主要信息找出来,形成副板书,重点形成文字语言与符号语言之间的转化.
四、二次函数的应用
本节课的课题是“二次函数的应用——经济类问题”,经历了很长时间的铺垫,现在才刚刚转回到正轨上.
问题呈现6:某商品的售价为x元,进价为3元,卖出2x件,利润为y元,请列出y与x的函数关系式.
同样经历信息的提取和副板书的书写过程,把相关字母放在相应的信息点下方,用公式(售价-进价)×数量=利润,这个问题就迎刃而解了.
设计意图:问题的设计采用循序渐进的方式,由小学算式过渡到列代数式,到一元一次方程,一元二次方程,二次函数,可以说一直在遵循从数到式的一个变化过程,把数式通性演绎到了极致.
试题的升华部分:
某商场经营某种品牌的童装,购进时的单价是60元/件,根据市场调查,在一段时间内,销售单价是80元/件时,销售量是200件,而销售单价每降低1元,就可多售出20件.
(1)写出销售量y(件)与销售单价x(元)之间的函数关系式;
(2)写出销售该品牌童装获得的利润w(元)与销售单价x(元)之間的函数关系式;
(3)若童装厂规定该品牌童装销售单价不低于76元,且商场要完成不少于240件的销售任务,则商场销售该品牌童装获得的最大利润是多少元?
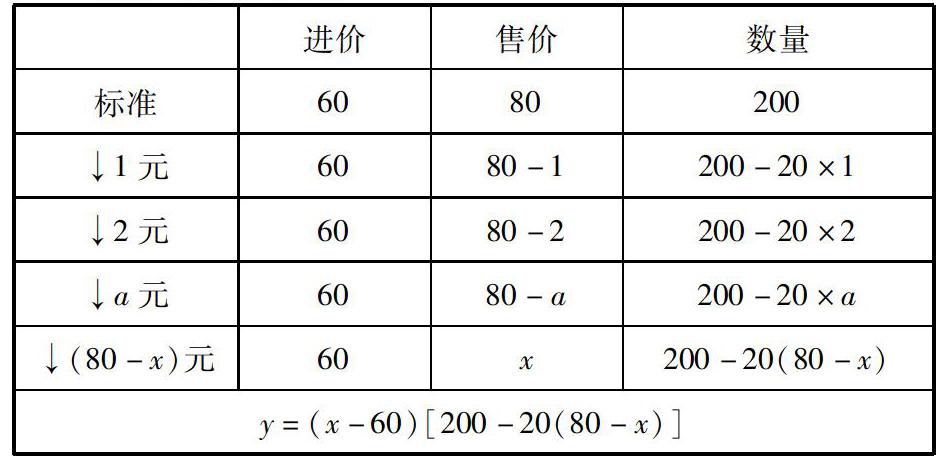
本部分板书设计:
进价售价数量
标准6080200
↓1元6080-1200-20×1
↓2元6080-2200-20×2
↓a元6080-a200-20×a
↓(80-x)元60x200-20(80-x)
y=(x-60)[200-20(80-x)]
这道习题的处理方式:先独立学习,在副板书的基础上,用符号与文字进行融合,逐一列在黑板上,如果其他同学有不同意见,再加以补充,完善.
设计意图:把完整的思考时间留给学生,让他们静静思考.因为数学是一个具有思维性的学科,静下来,慢下来是上课的主旋律,当学生经历了一定的思考,就会呈现适合自己的思考方式,再做一些对比分析,便能从中选择最优方案,从而达到对本节课知识进行一个深度理解的目的.
本节课的教学设计,采用低起点原则,让学生体验从特殊到一般的数学思想.数学建模是核心素养六大内容之一,也是知识体系中非常重要的一个环节.俗话说,数学来源于生活,数学处处为生活服务.与大家息息相关的利润问题,学生却迟迟找不到相关的解题思路,既复习了旧知识,又讲授了新知识,进而突破数学建模这一核心素养.
【参考文献】
[1]中华人民共和国教育部.数学课程标准(2011版)[M].北京:北京师范大学出版社,2011.

