基于多项式回归的压电式雾化片雾化速率校正方法*

纪永杰，骆德汉，温腾腾,钟平忠

(广东工业大学 信息工程学院，广东 广州 510006)

0 引言

经过多年对音频和视频信息的深入研究和探索，结合通信网络技术，人类的听觉和视觉功能己在时间及空间上获得了巨大的拓展[1-2]。与此同时，由于电子、计算机及信息技术的迅猛发展，机器嗅觉在国防、航空、生物医疗、智能家居、公共安防、食品安全、化工检测及多媒体等领域的应用也得到了世界各国的广泛关注[3-4]。

机器嗅觉主要包括气味的检测识别、网络化传输与终端复现[5]。在气味复现方面，气味发生器、嗅觉显示器已经有了初步的研究与探索，它是一种能够实时复现多种气味的新型仪器，在虚拟现实、电子商务等领域有广泛的应用前景[6]。如何精准“复现气味”越来越成为目前研究的热点。当前在仪器中实现气味散发的主要方式有：加热法、喷射法、阀门控制法、雾化法[7]。

采用多个压电式微孔陶瓷片构成超声波雾化阵列的方式因其驱动简单、绿色高效、雾化量可控等优点已经成为气味散发的首选方式。用于气味复现的雾化阵列结构如图1所示。然而在实际应用中，超声波雾化阵列的多个通道的雾化速率存在一定的偏移误差，且存在非线性关系，影响气味混合与释放的准确度。因此，需要对雾化阵列的雾化速率进行补偿校准。

本文在通过实验测量驱动电压与雾化速率关系的基础上，提出了基于最小二乘法的多项式回归模型来进行雾化速率校正，并通过实验进行了检验。

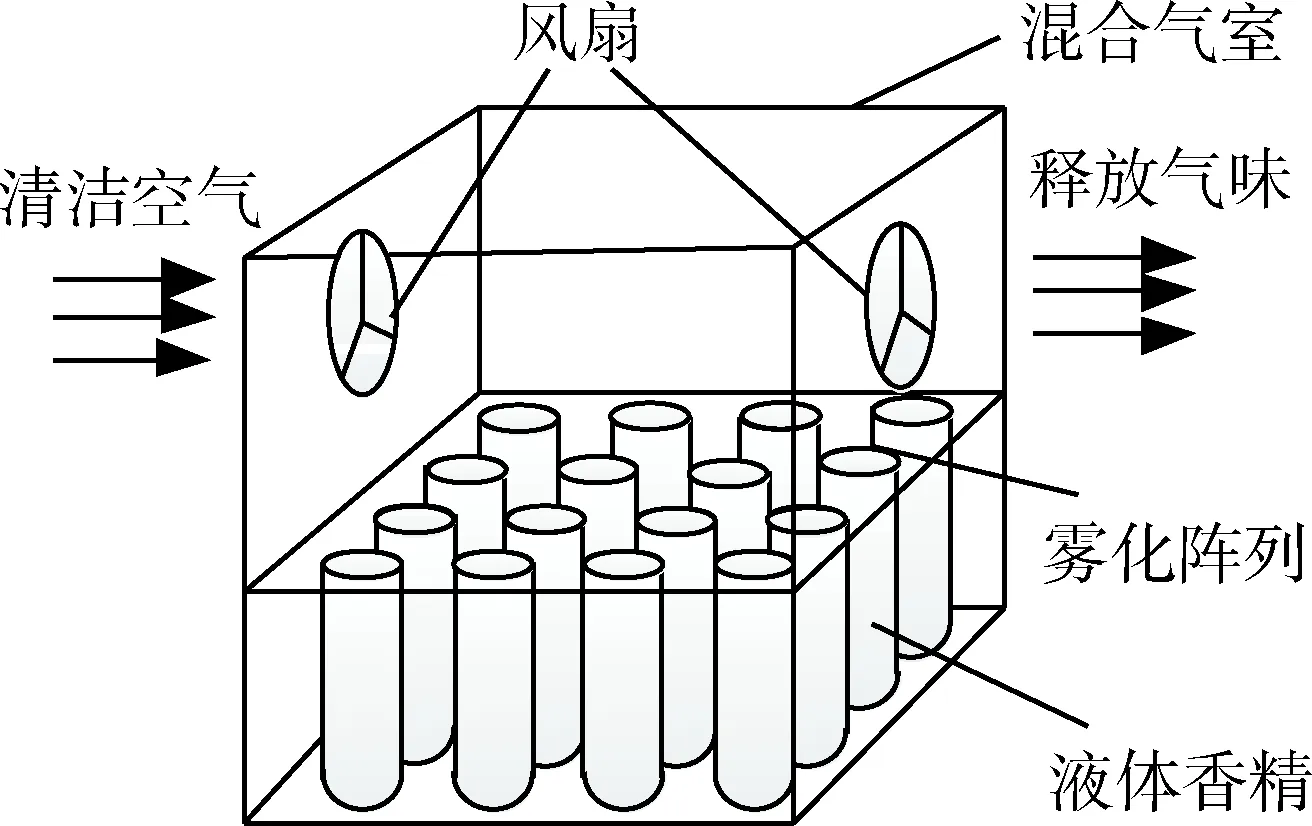
图1 气味复现仪器雾化阵列结构图

1 误差分析与数据采集

1.1 雾化速率影响因素分析

由于逆压电效应，对压电敏感元件施加变化的电场会引起元件的机械形变。压电陶瓷具有将电能转换为机械能的能力，它将高频震荡波的电能转换为液体颗粒振动的机械能，因此高频方波驱动压电微孔陶瓷片是实现超声波雾化的方式之一[8]。

张建桃、汤镇安等人通过实验分析了液体物理性质、孔径大小、驱动电压、驱动频率等因素对压电式微孔陶瓷片雾化效果的影响[9]，他们发现，雾化速率随着驱动电压或驱动频率的增加先增大后减小，驱动电压与驱动频率对雾化速率有明显影响，且呈非线性关系，但是没有用数学模型描述这种关系,也没有考虑棉棒与压电陶瓷的松紧压力对雾化速率造成的影响。

图2是雾化阵列的微孔压电陶瓷片驱动电路，信号源提供方波信号控制MOS管(CJ3400)的导通与关断，通过高频变压器进行电压放大后驱动微孔压电陶瓷片(M1)。微孔压电陶瓷片正常雾化的驱动电压幅值为200 V左右，设计的变压器匝数比为30∶185，放大倍数约为38倍。驱动电路器件参数误差、变压器加工误差、压电陶瓷的工艺差异、棉棒与压电微孔陶瓷的接触松紧均对雾化速率有不同程度的影响。

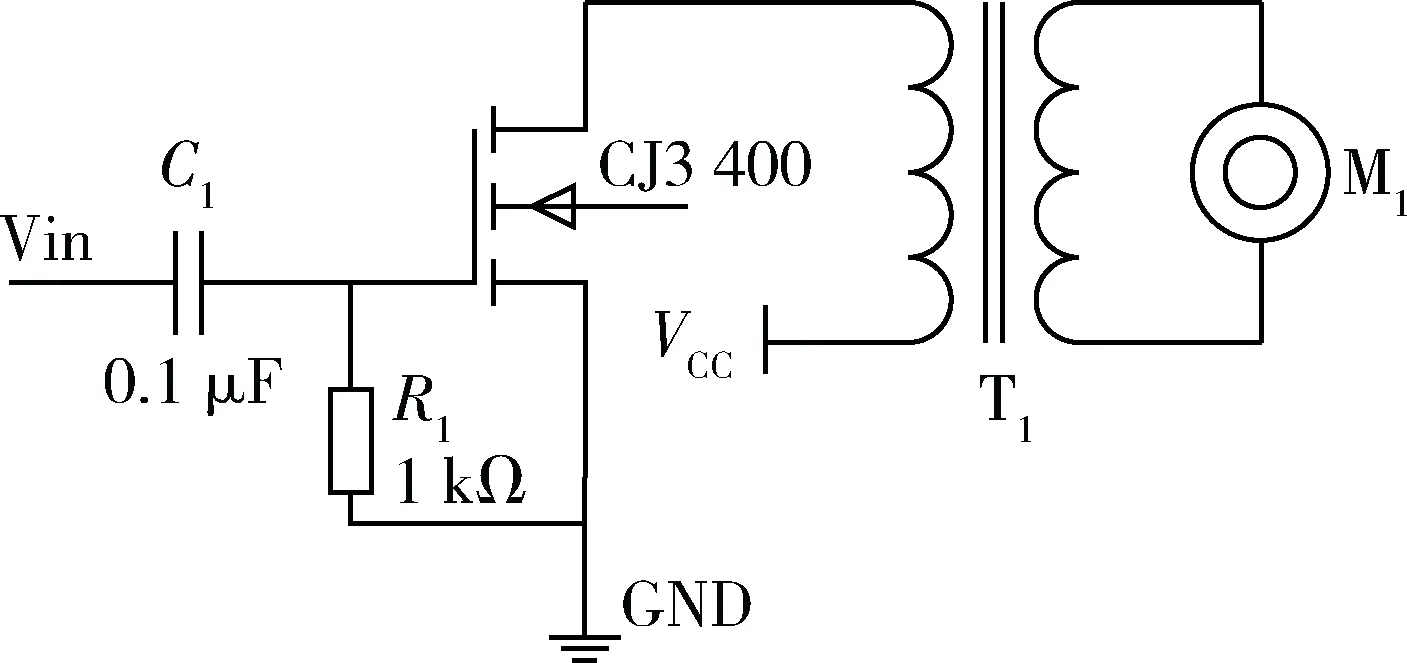
图2 微孔压电陶瓷片驱动电路

1.2 实验系统框架

为测定雾化速率随驱动电压的变化关系，设计了一个实验数据采集系统，系统框图如图3所示。实验前，采用Analog Discovery网络分析仪测量的微孔压电陶瓷片的谐振频率为113 kHz。给驱动电路提供113 kHz的驱动信号，驱动信号可以采用主控器加频率合成器的方法产生[10],但是它需要设计额外的电路。而采用搭载ZYNQ-7000处理器的Arty Z7开发平台的FPGA模块生成需要的113 kHz信号，不仅可编程实现，并且无需设计额外的电路。驱动电路的电源电压由PWM信号控制的可调电源提供，PWM调压信号同样由Arty Z7产生，可控制电压在0 V～10 V内连续变化。

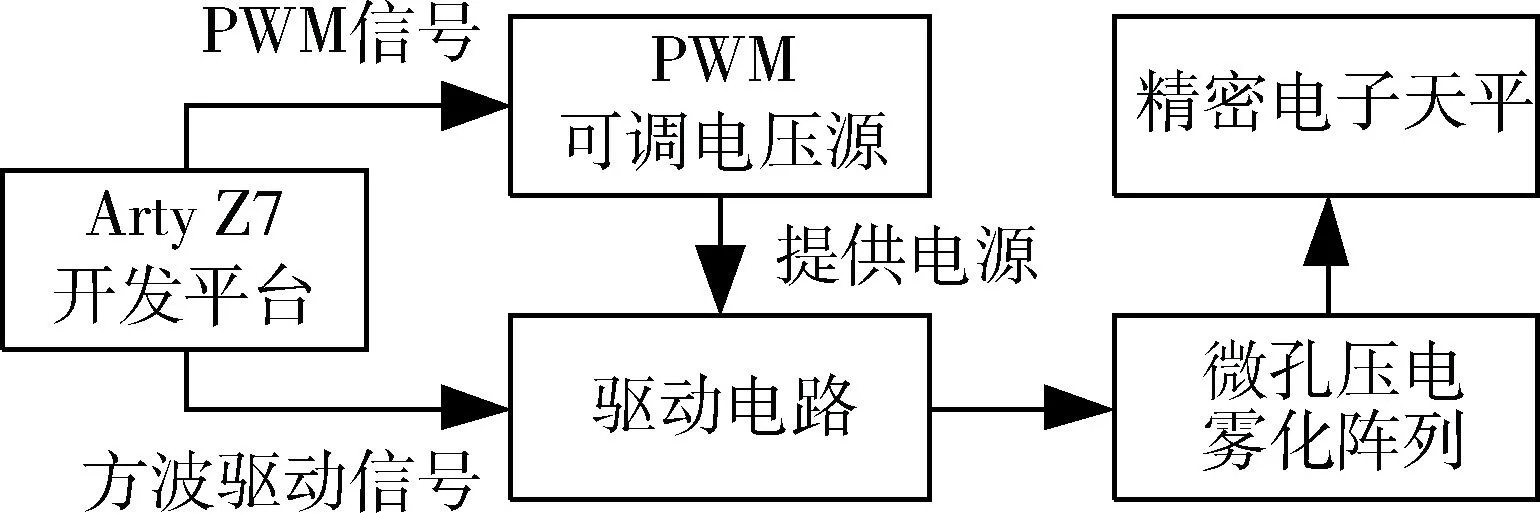
图3 实验系统框图

气味复现仪器的香料雾化阵如图1所示，总共16个雾化通道，采用一致的驱动电路与器件。雾化通道结构如图4所示，液体香料存放于香料容器中，被圆柱型棉棒吸附后与压电式微孔陶瓷接触雾化。

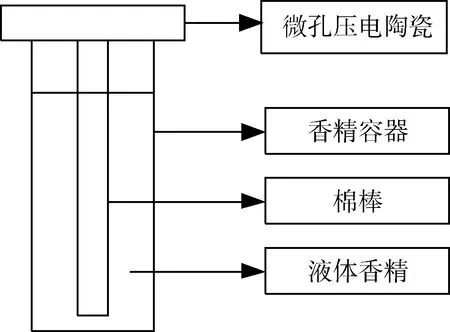
图4 雾化通道结构图

本文随机选取3个雾化通道作为实验对象。雾化速率以单位时间(5 min)内容器中液体质量减小的程度来度量，采用精度为0.01 g，量程为2 kg的高精度电子天平测量，以确保微小质量的变化的测量准确性。

1.3 实验数据采集

为了降低空气流动对雾化效果与电子天平的影响，实验选择在周围气流稳定密闭房间内进行。由于驱动电压与驱动频率均会对雾化速率产生影响，实验过程中采用控制变量法，固定驱动方波频率为谐振频率113 kHz，驱动电压(这里指变压器原边电压)设置在雾化片能正常工作的电压范围(1.7 V～6.8 V)内均匀变化，每次变化量为0.3 V，分别测量雾化5 min后的液体质量差。3个雾化通道分别采集18个数据，最终获得3组样本。

实验数据如表1所示。通过分析实验现象，发现当驱动电压较低时(低于1.7 V左右)，雾化速率变化很慢，液体颗粒渗出雾化片表面，难以形成雾化液滴喷出；当驱动电压继续增大时，雾化速率随驱动电压增大而迅速提升，当驱动电压过大时(大于6.8 V左右)，雾化片迅速发热致使用于吸附液体的棉棒变形[9]，且受限于雾化片微孔孔径大小，雾化速率趋于平稳。

表1 驱动电压与物化速率关系

2 校正模型建立

2.1 最小二乘法的多项式拟合模型

通过实验获取了雾化速率与驱动电压的变化规律之后，本文的目标是找到一种描述这种规律的方法并建立相应的数学模型，根据模型数据采用调节驱动电压的方式对不同雾化通道的雾化速率进行校准。通过分析雾化速率与驱动电压的关系曲线，采用一元多项式回归(Polynomial Regression)模型来描述固定驱动频率下雾化速率与驱动电压的非线性关系[11]较为理想，并且通过最小二乘法计算多项式系数。

最小二乘法(Least Squares)提供了一种多项式系数的求解方法,其基本思想就是寻找“最接近”n个观测点的直线,以误差平方和最小为原则选取最佳的拟合曲线[12]。利用最小二乘法可以简便地求得预测数据，并使得求得的预测数据与实际数据之间误差的平方和为最小。

设拟合多项式为：

y=a0+a1x+…+akxk

(1)

其中x为自变量，y为因变量，ai为待求的二项式方程的系数，最高项次数为k，各点到这条曲线的距离之和，即误差平方和R2如下：

(2)

为求得使偏差平方和最小的a值，分别对等式右边求ai的偏导数，并简化到下面等式：

(3)

将上述等式表示成矩阵的形式，可以得到下面的矩阵：

(4)

将此范德蒙矩阵化简后，可得到：

(5)

解此方程即可得到多项式的系数。

2.2 模型参数计算

为方便求解多项式拟合模型的参数ai，采用MATLAB软件的函数polyfit计算[11]，数据由表1给出，简要的计算过程如下：

X=[x1,x2,x3,…,xn]

(6)

Y=[y1,y2,y3,…,yn]

(7)

P=polyfit(x,y,k)

(8)

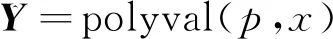
(9)

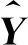
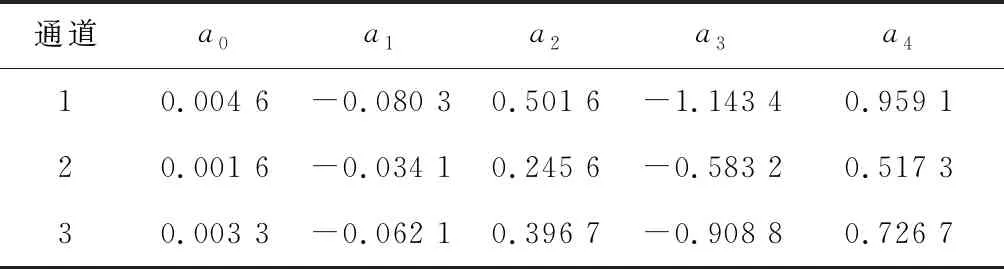
表2 四次多项式模型参数表

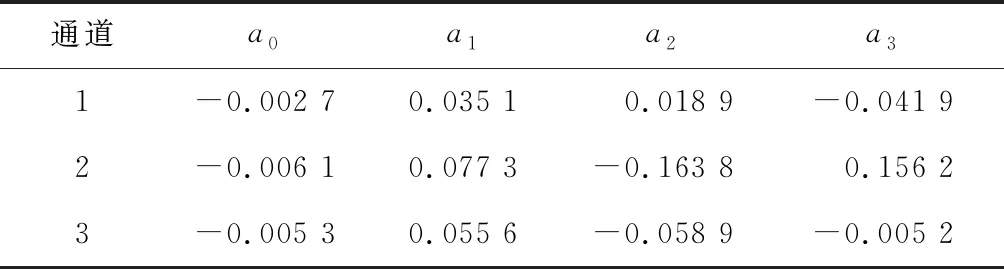
表3 三次多项式模型参数表

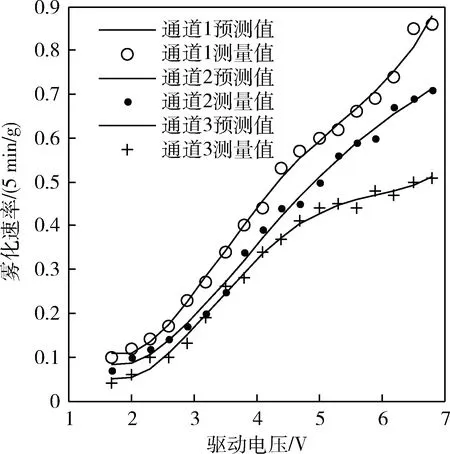
图5 四次多项式拟合曲线图

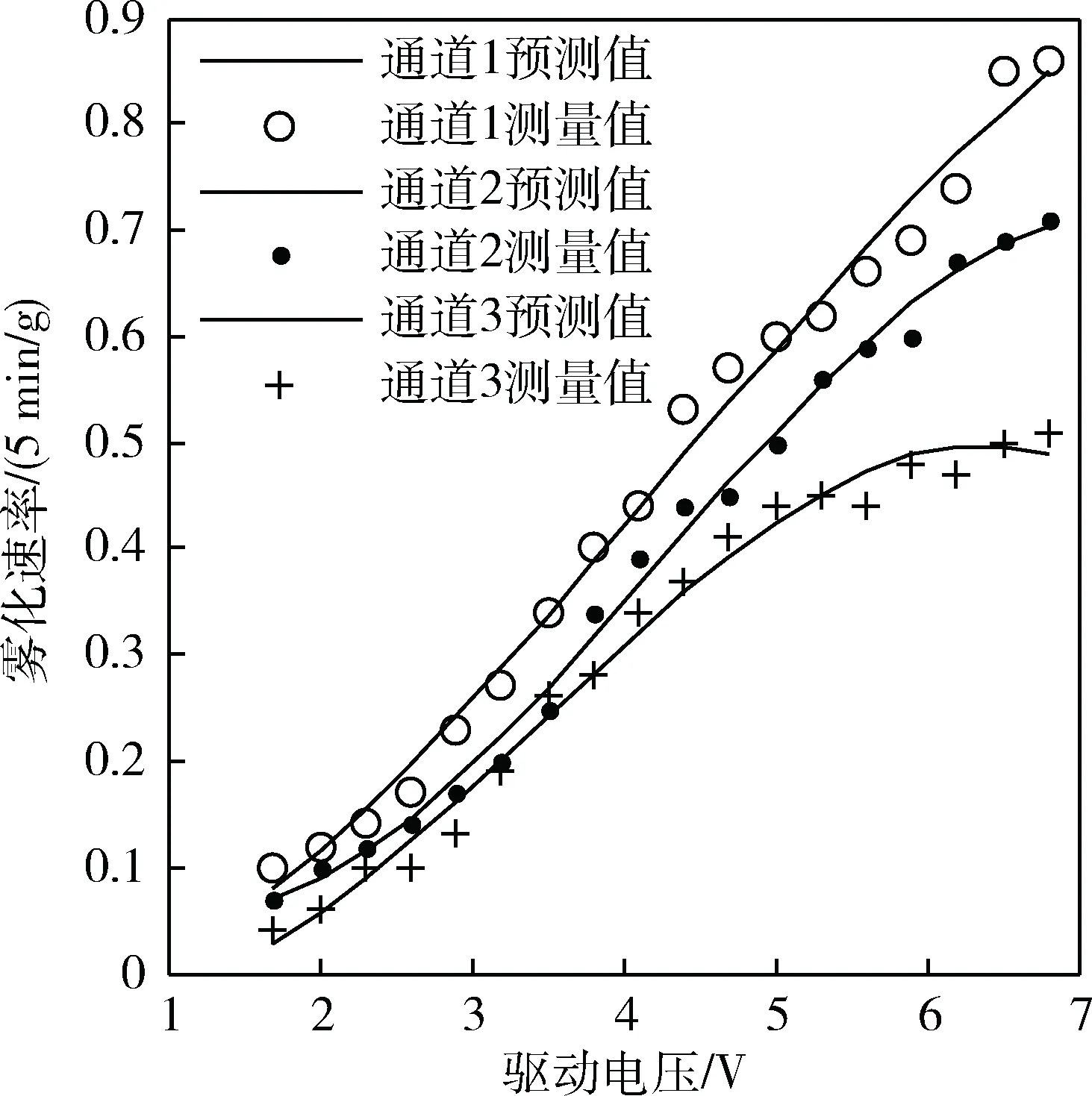
图6 三次多项式拟合曲线图

2.3 拟合模型评价

在评价回归模型的效果时，常用方法有：均方根误差RMSE(Root Mean Squared Error)、平均绝对百分比误差MAPE(Mean Absolute Percent Error)[13-14]、决定系数R-Squared来评价回归模型的准确性。均方根误差对一组测量数据中的特大或特小误差反应非常敏感，能够很好地反映回归的精度。平均绝对百分比误差表示预测值与真实值的误差百分比。决定系数用来描述模型的准确度。均方根误差与平均绝对百分比误差越小，绝对系数越接近1，代表模型的准确度越高。计算公式如下：

(10)

(11)

(12)

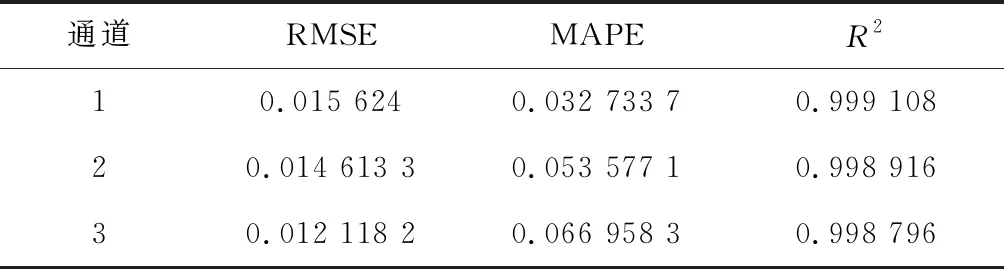
表4 四次多项式模型评价指标

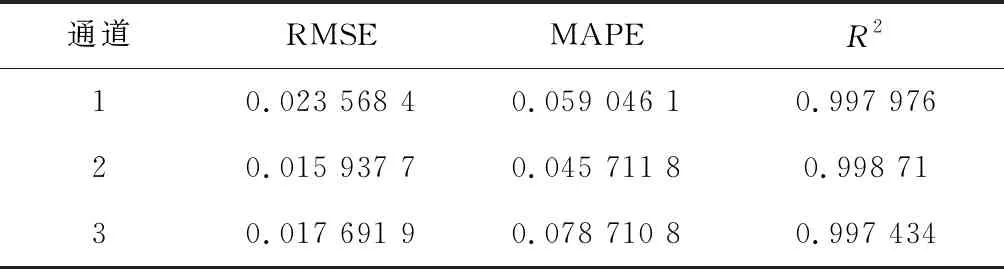
表5 三次多项式模型评价指标

根据计算结果可知，四次多项式的回归效果优于三次多项式，均方根误差小于0.02，误差百分比小6%，决定系数接近1，可以准确地描述驱动电压与雾化速率的变化关系。

2.4 补偿方法

雾化速率补偿方法如图7所示，计算出每个通道的多项式回归模型系数后，通过MATLAB计算出每个雾化速率值所映射的驱动电压值。将每个通道的模型数据文件存储于Arty Z7的文件系统中，系统上电后，读取数据存入哈希表，输入雾化速率校正值，通过查表[15]的方式确定每个通道要达到雾化速率校正值所需要的驱动电压值。

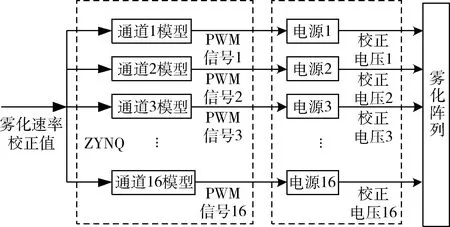
图7 补偿方法框图

3 实验验证

为了验证多项式回归校正模型校正雾化速率在实际应用中的有效性，选取雾化速率为0.3 g/5 min、0.4 g/5 min、0.5 g/5 min为校正目标，通过校正模型分别计算出3个通道在雾化速率为0.3 g/5 min、0.4 g/ 5 min、0.5 g/5 min时对应的驱动电压，测量对应驱动电压的雾化速率以验证校正效果。实验结果如表6、表7所示。由表7数据可计算雾化速率校正误差(实际测量值与校正值的差值)，通道1雾化速率校正误差最大为0.01 g/5 min，通道2雾化速率校正误差最大为0.02 g/5 min，通道3雾化速率校正误差最大为0.02 g/5 min。由此可见，采用多项式回归模型校正后，雾化速率误差最大值约为0.02 g/5 min，可满足实际应用的要求。

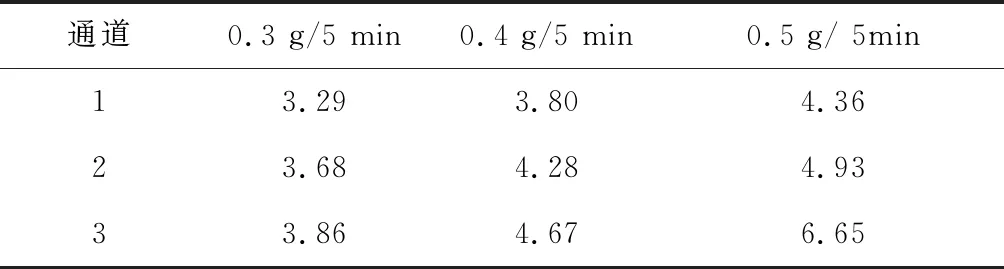
表6 驱动电压校正值(V)

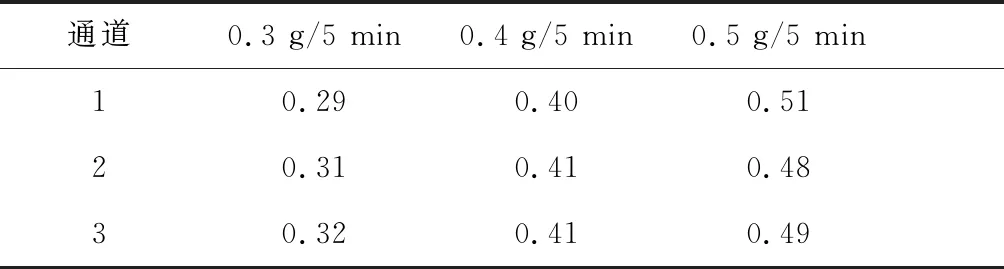
表7 雾化速率校正值(g/5 min)

4 结论

本文基于气味复现仪器中压电式微孔陶瓷不同通道的雾化速率漂移问题，构建了基于最小二乘法的多项式回归校正模型。分别评估了三次多项式与四次多项式模型的性能，并最终采用四次多项式模型，通过实验验证雾化速率误差最大值可满足实际应用的要求，表明了校正模型能有效降低不同通道的雾化速率误差。