一种基于图结构的网络信息体系项目管理复杂性度量方法

杨德庆

(中国武警部队参谋部，北京 100089)

0 引言

网络信息体系是我军未来建设和发展的重点。而其建设是一项复杂的体系工程，主要体现在工程规模大、技术种类多、持续时间长、项目参与单位广、建设环境复杂。受需求变更、研制目标、外部环境、部门沟通协调等多种不确定因素的影响，工期延误、成本超支、沟通协作交接不畅等问题给工程建设带来了许多新的挑战和风险，增加了工程项目的复杂性。研究表明，项目的成功与项目的复杂性密切相关，传统的项目管理方法已不足以适应当前项目的复杂性。因此，需要发展项目管理学科的新理论、新方法，来应对项目复杂性问题的挑战，越来越多的人开始认识到项目复杂性对项目的顺利完成有着决定性影响。

国内外许多专家学者已经对工程项目的复杂性及其管理复杂性进行了大量研究。BOSHC-REKVELDT M[1]探讨了工程项目复杂性的框架，从技术、组织、环境三个方面进行了深入分析。VIDAL L A等人[2]认为项目复杂性的驱动因素与项目大小、种类、项目间关系以及环境有关，并且利用层次分析法来评估项目复杂性。BACCARINI D[3]认为复杂性对项目管理过程的重要性已经形成共识。例如，项目复杂性直接决定着计划、协调、控制的要求，能够影响项目在时间、成本、质量等方面的目标识别。WYSOCKI R K[4]指出传统的项目管理模型(Traditional Project Management，TPM)已经不适合应用的需求并提出了一种新的项目管理方法：适应性项目框架(Adaptive Project Framework,APF)。张宪[5]认为项目管理复杂性已经成为了项目管理研究前沿和热点。乐云[6]认为项目复杂性给项目管理带来了新的挑战。BOUSHAALA A[7]认为项目复杂性表现在两方面，分别是技术复杂性和管理复杂性，其中，技术复杂性影响着工程建设的困难程度，管理复杂性影响着项目的进度、成本、风险和沟通等，并构建了网络复杂性系数(Coefficient of Network Complexity，CNC)来衡量复杂性。JAAFARI A[8]认为传统的项目管理方法面临着严重挑战，急需对项目管理重新定义，加强应对复杂社会挑战的问题研究，并从诊断学的理论和应用方面评估了项目在寿命期间的健康程度。

网络信息体系项目管理涉及需求、项目范围、项目进度、成本、质量、风险、物资、人力资源、信息沟通、项目协作等内容，具有管理对象种类多、要素层次关系错综复杂、受环境影响不断演化的特点，是一个典型的开放式复杂巨系统，主要面临三个层面挑战：一是项目层面，整个项目表象是单个项目，实质上是由众多不同特点、不同层次的项目(课题)组成的复杂项目群，既包括体系、系统、分系统、装备、模块、元器件等不同层次的项目，也涉及科技创新、工程研制等不同类型的研制任务；二是组织管理层面，项目组织体系由跨领域、跨单位的众多研发团队联合承担，需要对各层各类项目相关范围、进度、成本、质量、资源、信息、风险进行有序的集成化管理，确保项目管理活动的高效性；三是技术层面，应按照体系工程方法有序推进，即以能力定义为起点，通过顶层设计，提出统一的架构体系与标准体系、关键技术与产品体系，规范各层次产品研制和体系建设，并增量式地集成以交付最终“能力”。因此，对于网络信息体系项目管理的研究，必须运用复杂网络和复杂系统理论为指导，通过引入耗散结构、突变论、自组织、涌现性等复杂性理论，开展网络信息体系项目管理复杂性研究，为在网络信息体系项目管理中更好地评估和降低复杂性提供理论和方法指导。

本文针对网络信息体系项目管理复杂性如何刻画、分析以及度量等基础问题，分析了网络信息体系项目管理的复杂性和复杂性指标体系，提出了基于图结构的网络信息体系项目管理复杂性度量方法，揭示复杂性在网络信息体系项目管理全寿命周期中的发展演化机制，为网络信息体系项目的复杂性管理提供参考和依据。

1 网络信息体系项目管理复杂性结构

针对网络信息体系项目管理的复杂性，基于项目全寿命周期的管理角度，从工程规划计划管理、研制阶段管理、研制项目管理、体系运行管理4个方面，建立网络信息体系项目管理复杂性度量模型，如图1所示。

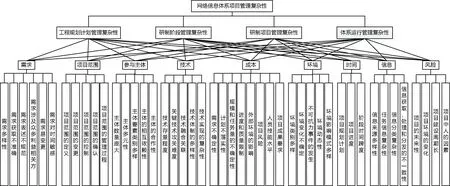
图1 网络信息体系项目管理复杂性度量指标体系

按照复杂性理论，系统复杂性来源于系统的规模、结构、环境、运行、演化以及人的理性的复杂性等方面。网络信息体系项目管理的规模，项目参与主体相互关联、相互制约，体系建设过程中受到外界环境的影响，以及在工程建设中，在不同的层次和位置上，如进行项目决策、任务执行、信息处理、上报等环节，均可能存在人的因素，这些都对应了复杂性来源理论。结合网络信息体系项目管理对象和运行模式，将其复杂性来源分别归纳为需求、项目范围、参与主体、技术、成本、环境、信息、风险等9个因素，通过进一步细化分解可构建网络信息体系项目管理复杂性度量评估指标体系。其中，需求因素主要包括需求多样性、需求获取不准确、需求表述不规范、需求涉及众多利用相关方、需求易变更、需求对时间敏感等指标；项目范围因素主要包括项目范围的定义、项目范围的变更、项目范围的控制、项目范围的确认、项目范围的管理过程等指标；参与主体因素主要包括主体数量庞大、主体多元性、主要要素类别多样、主要的相互依赖、主要的合作性等指标；技术因素主要包括技术存量程度、关键技术攻关难度、技术融合关联、技术体制的多样性、技术实现的复杂性等指标；成本因素主要包括需求不确定性、计划不落实性、规模和任务量的不确定性、进度和质量限制、项目风险、人员技能水平、项目成果要求等指标；环境因素主要包括环境类别多样、环境变化不确定、不可抗力事件的发生、环境动态性、环境影响模式多样等指标；时间因素主要包括项目规划计划、项目进度、阶段时间跨度等指标；信息因素主要包括信息来源多样性、任务信息复杂性、信息分类复杂性、信息获取、处理和分发的不一致性等指标；风险因素主要包括项目的未来性、项目环境的变化、项目建设周期长短、项目中人的因素等指标。

2 基于图结构的网络信息体系项目管理复杂性度量方法

通常，简单系统的复杂性可用简明的指标公式来表征；而复杂系统的复杂性可能涉及多种因素，因此需要从多个角度来衡量这种复杂性。体系的复杂性越高，其不确定性却大，而要确实掌握体系的状态所需要的信息量也就越大。因此，可以用熵理论来分析度量网络信息体系项目管理的复杂性。

由信息论可知，给定随机矢量H(A)，Shannon熵定义为：

H(A)=-∑pa(a)logpa(a),a∈A

(1)

其中，pa(a)是随机矢量A中元素a的概率分布函数。熵H(A)表达的是矢量A所代表的系统的不确定性。

下面将网络信息体系项目管理复杂性度量问题抽象成图结构，即节点和连边的结合。建模过程如下：图1树状图中的每一个节点表示图结构的一个节点，图1中的分枝表示图结构中的连边，可构建项目管理复杂性图结构模型。

假设节点的集合为s={s1,s2,…,sn},权重集a={a1,a2,…,an}表示节点的重要程度，其中ai为节点si的权重；同时，假设节点间关系的种类为r={r1,r2,…,rm}，权重集b={b1,b2,…,bm}表示关系重要程度，其中bj为关系rj的权重。对于树状层级结构，存在以下关系，分别是：r1表示直接控制关系，r2表示直接从属关系，r3表示间接控制关系，r4表示间接从属关系，r5表示在较高层次的并列关系，r6表示在较低层次上的并列关系，r7表示在同一层次上的并列关系。显然，m的最大值为7。符号rj(si)表示与si有关系rj的序对(si,sk1)，(si,sk2)，…，(si,skj)，并用Lij表示这些序对的个数。

基于Shannon的信息熵公式，在节点si上的关系rj的熵定义为：

(2)

(3)

构建连边矩阵Rj(j=1,2,…,7)，

连边矩阵Rj的元素

(4)

如前所示，Lij表示在连边rj上的序对(si,sk)的个数，可建立长度矩阵L，即L=[Lij]n×7。

由连边关系矩阵Rj(j=1,2,…,m)，长度矩阵L的元素为：

(5)

考虑到控制与从属关系是对称的，用符号“～”表示对称关系，则有r1～r2，r3～r4，r5～r6，可得到矩阵R1，R3，R5是上三角矩阵，矩阵R2，R4，R6是下三角矩阵，在关系r1∪r2意义下，有R1′=R1+R2，类似地，有R2′=R3+R4，R3′=R5+R6，R4′=R7，得到四个对称矩阵。

(6)

由连边关系矩阵R4，当j=4时，有

(7)

下面考虑节点和连边的权重情形，建立权重矩阵A和B来修改长度矩阵L，有：

L′=A×L×B

(8)

其中，A是以a={a1,a2,…,an}为对角元素的对角矩阵，B是以b={b1,b2,…,b7}为对角元素的对角矩阵，长度矩阵L的元素为：

Lij′=ai×Lij×bj

(9)

此时，熵矩阵元素

(10)

熵矩阵为：

H=[Hij]n×7

(11)

求得网络信息体系项目管理的复杂度为

(12)

3 结论

本文针对网络信息体系项目管理复杂性建模方法展开研究，着眼网络信息体系复杂性如何刻画、分析以及度量等基础问题，分析了网络信息体系项目管理的复杂性，对网络信息体系项目管理的复杂性提出了评价指标体系，构建了基于图结构的项目管理复杂性测量方法，为在网络信息体系建设中更好地限定和利用复杂性提供理论和方法指导。