推导矩形边界磁场对各边导线产生的电动势

郑 金

(凌源市职教中心 辽宁 朝阳 122500)

1 提出问题

对于有界磁场随时间均匀变化而产生感应电动势的问题，如果磁场边界为矩形，那么对位于边界的导线框各边分别产生的感应电动势的大小无法应用初等方法来求解，而需应用麦克斯韦电磁场理论和高等数学中的微积分知识进行定量推导.

鉴于文献[3]～[5]中的推导过程大都省略了数学微积分部分而显得不完整，下面通过对一道例题的解答进行详细推导和计算,使数学和物理结合得更加完美.

2 例题的错解与辨析

【例题】如图1所示，用均匀金属导线做成的正方形线框，边长为0.2 m，有一半放在匀强磁场边界，当磁感应强度以k=10 T/s的变化率均匀增强时，线框的中线MN两端的电势差UMN是多少？

图1 例题题图

解法1:将左半部分电路MADN视为电源，右半部分电路MFCN视为外电路.磁场区域的面积为

S=0.2×0.1 m2=0.02 m2

由法拉第电磁感应定律可知感应电动势为

由楞次定律可知感应电流沿逆时针方向，则N点的电势比M点的电势高.由于内、外电阻相等，即R=r，可得路端电压为

UNM=ε-Ir=0.5ε=0.1 V

所以

UMN=-0.1 V

辨析:虽然线框右半部分导线MFCN在磁场之外，但也产生感应电动势.因此算得电动势是整个回路的总电动势，不能作为左半部分电路的电动势.

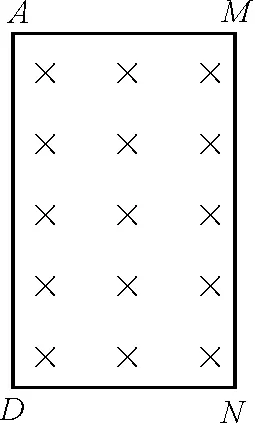
图2 图1的等效图

辨析:由于矩形边界的磁场产生的涡旋电场不是匀强电场，那么在AM,MN两边各自产生的感应电动势并非与直导线的长度成正比，因此,不能认为长边产生的电动势等于短边产生的电动势的2倍.

该题实际是求解位于磁场边界的矩形线框各边在涡旋电场中产生的电动势，无法用初等方法解答，只能应用大学物理知识和高等数学知识进行推导.

3 圆形边界磁场随时间均匀变化时产生的涡旋电场

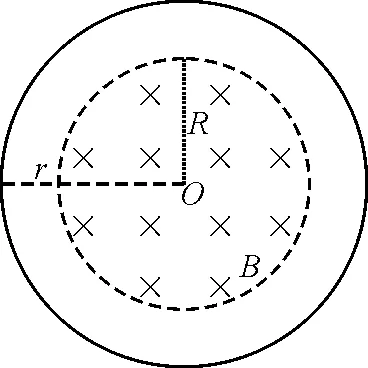
图3 圆形边界磁场与导线环示意图

当圆形边界的匀强磁场均匀变化时，产生涡旋电场的电场线是系列同心圆，因此导体圆环与一条电场线重合，则圆环上的场强大小处处相等.假如导线环有一个很小的缺口，那么感应电动势等于缺口两端的电势差，跟匀强电场中的电势差公式U=Ed类比可知，导线环两端的电势差在数值上等于导线环上的场强与路径长度的乘积，因此感应电动势与场强的关系为

ε=El=2πrE

可知圆形涡旋电场的场强为

各种图形边界的匀变磁场激发的涡旋电场在闭合回路中产生的感应电动势可用微积分表示为

ε=∮lEdl

(1)

4 用涡旋电场和场的叠加原理对例题进行深度解析

首先推导涡旋电场强度分量表达式，然后推导各边的电动势的表达式，最后求出数值.

对图2建立空间直角坐标系如图4所示，为右手系，可知z轴方向垂直于纸面向外，与磁场方向相反，则有B=-B(t)k.当矩形边界的匀强磁场随时间均匀变化时，产生涡旋电场的电场线不是同心圆.

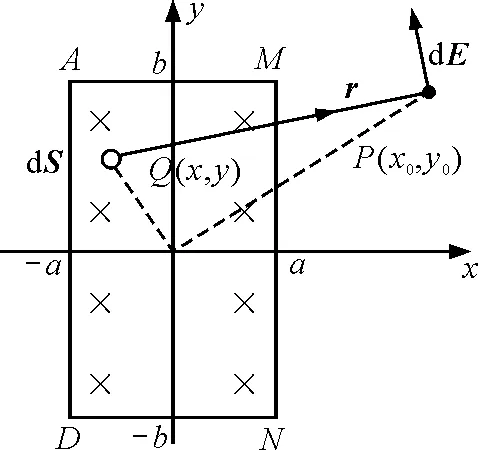
图4 建立右手空间直角坐标系

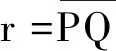
两式联立可得

(2)

位矢r的方向由Q指向P，考虑到dE→r→B三者方向关系遵循右手螺旋定则，则场强的矢量式为

(3)

由电场叠加原理可知，整个矩形截面S区域内的磁场在P点激发的感应电场的强度为

(4)

Q到P的位矢用坐标轴方向的单位矢量表示为

r=(x0-x)i+(y0-y)j

代入式(4)可得P点的电场强度为

E(x0,y0)=

由于叉积i×k=-j，j×k=i，则有

E(x0,y0)=

(5)

可知电场强度在x轴方向的分量为

设矩形区域沿x轴方向的长度为2a，沿y轴方向的长度为2b，磁场微元的面积大小为dS=dxdy，即得

(6)

令F(y)=(x0-x)2+(y0-y)2，取微分，得

dF(y)=-2(y0-y)dy

即

当y=-b时

F1(y)=(x0-x)2+(y0+b)2

当y=b时

F2(y)=(x0-x)2+(y0-b)2

将各式代入式(6)可得

即

(7)

再令X=x0-x，则dX=-dx，当x=-a时，X1=x0+a;当x=a时，X2=x0-a,可知

(8)

由于导线AM位于磁场的上边界，则y0=b，应用积分公式

对式(8)进行积分并整理得

(9)

在涡旋电场中，一段导体产生的电动势为

对于导线AM，若积分路径为M→A，则有

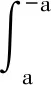
(10)

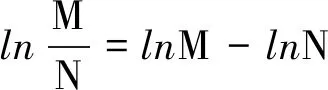
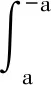
利用积分公式

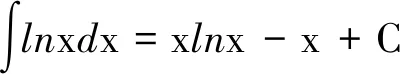
得

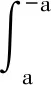
令

[(x0-a)2+4b2]=X

则有

可得

2(a2+b2)ln(4a2+4b2)-2a2-4b2ln2b

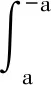
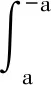
4b2ln2b-2(a2+b2)ln(4a2+4b2)+2a2

考虑到反正切函数是奇函数，可得

利用积分公式

得

综上可知导体AM产生的感应电动势为

即得

ln(4a2+4b2)-2a2ln2a+2b2ln2b]

(11)

同理得

ln(4b2+4a2)-2b2ln2b+2a2ln2a]

(12)

这就是矩形边界磁场随时间均匀变化时位于边界的矩形线框各边产生的感应电动势的计算公式.

把a=0.05 m,b=0.1 m,k=10 T/s代入式(11)，并将arctan 0.5=26.565°化为弧度，可得

εMA=εDN≈0.035 3 V

由法拉第电磁感应定律可得回路中的感应电动势为ε=0.2 V.则

ε=2εAM+2εNM=0.2 V

由此可知NM边的电动势为

εNM≈0.064 7 V

设电路的总电阻为r，对应图2的等效电路如图5所示.由闭合电路欧姆定律可知

UMN=εMN-IrMN≈

0.064 7 V-0.1 V=-0.035 3 V

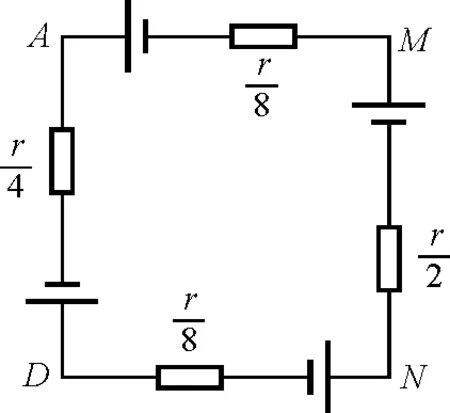
图5 图2的等效电路图

5 结束语

利用麦克斯韦电磁场理论无法直接求出矩形线框的总电动势，但可分别求出矩形线框各边产生的感应电动势，取代数和即为总电动势;利用法拉第电磁感应定律不能分别求出矩形线框各边导体产生的电动势，但可直接求出线框的总电动势，二者所得结果完全相等，可谓殊途同归，互为验证.对于矩形边界磁场激发的涡旋电场在矩形线框各边分别产生的感应电动势的大小是否跟导线的长度成正比，只能进行详细的定量推导，通过具体的物理情境使得有关物理和数学知识在实际应用中完美结合.