基于牛顿环等厚干涉的数值分析*

杨利利

(宁夏大学物理与电子电气工程学院 宁夏 银川 750021)

在牛顿环等厚干涉实验中，可观察到干涉条纹是以接触点为中心的一系列同心圆环，且干涉圆环明暗相间，内疏外密.若采用不同曲率半径的透镜进行实验，则观察到干涉圆环半径也不同[1].本文重点分析不同曲率透镜下牛顿环等厚干涉圆环的半径及相邻明环或暗环的间距，获悉牛顿环等厚干涉的特点，揭示其中蕴含的规律，帮助学生正确理解实验现象.

1 牛顿环等厚干涉原理

牛顿环等厚干涉原理图如图1(a)所示[2,3]，一曲率半径较大的平凸透镜的凸面与平面玻璃之间形成空气薄膜.当单色平行光垂直照射牛顿环时，入射光在空气薄膜上表面部分被反射.另一部分折射后又被空气薄膜下表面反射，并与上表面反射光相遇，如图1(b)所示.

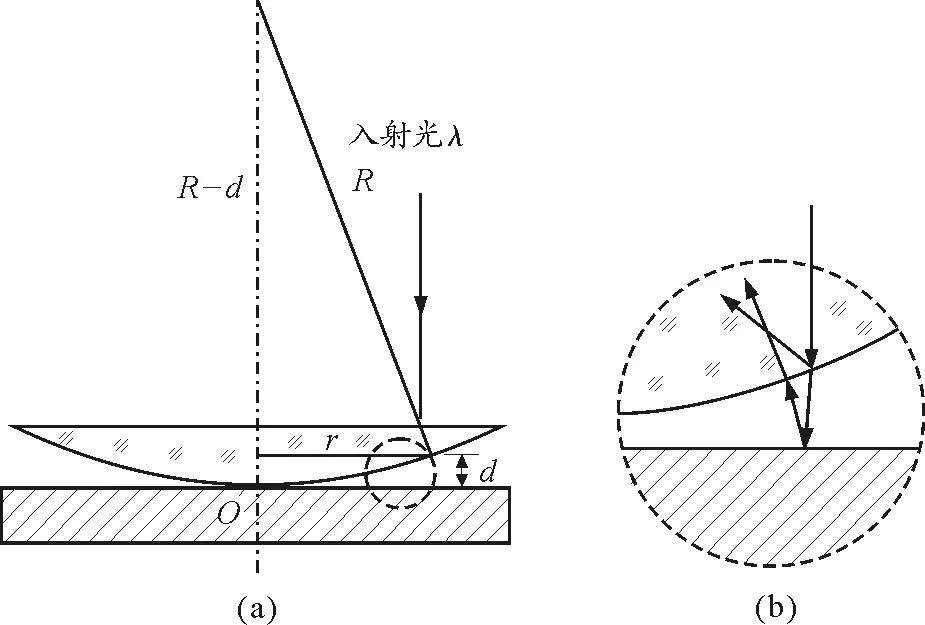
图1 牛顿环等厚干涉原理图

若该两束反射光满足相干条件，相遇后则产生如图2所示的干涉图样.

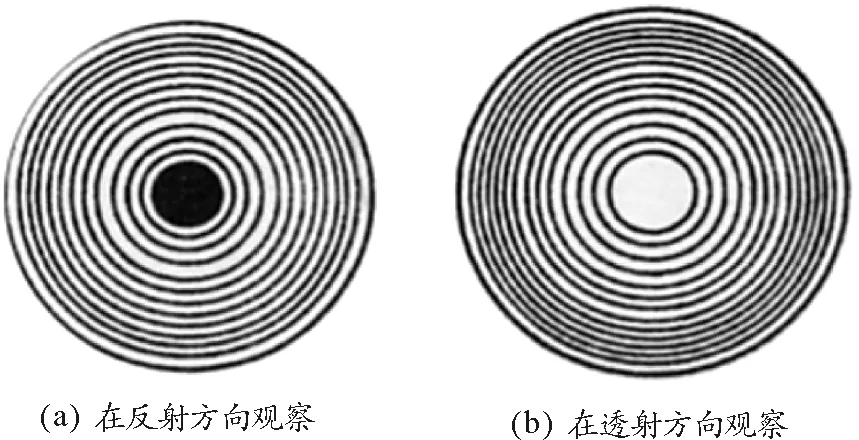
图2 牛顿环等厚干涉图样

显然，空气薄膜厚度d相同的点，形成同一级干涉圆环，此时对应两束反射光的光程差为[4,5]

(1)

而产生明、暗纹的条件即光程差与波长之间的关系为

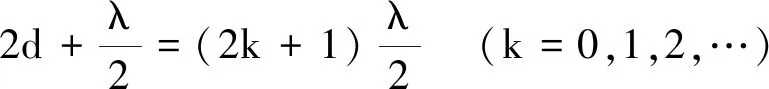
(2)

(3)

2 干涉圆环半径的数值分析

若已知牛顿环仪平凸透镜的曲率半径为R，k级干涉条纹的半径为rk，则由几何关系可得

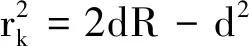
(4)

因为空气薄膜的厚度d远小于透镜的曲率半径R，即d≪R,忽略式(4)中的二阶无穷小量，可得

(5)

联立式(2)、式(3)和式(5)，并消去公式中的d，则形成的k级干涉暗纹半径rk和明纹半径r′k分别为

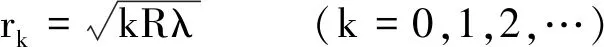
(6)

(7)

式(6)和式(7)表明，牛顿环等厚干涉圆环半径与入射光波长λ、透镜曲率半径R以及干涉级次k有关.为了探究干涉圆环半径r与透镜曲率半径R之间的关系，本文采用单色钠光源，以排除不同光源的干扰[6].若以干涉暗环为例，通过理论计算，利用Origin软件绘图，分别在不同透镜曲率半径下讨论干涉圆环半径的变化规律,如图3所示.

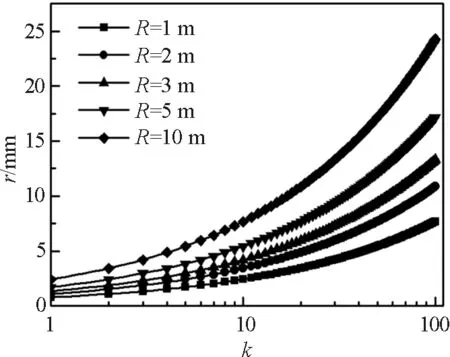
图3 不同R对应干涉暗环半径随k的变化

由图3可知，对于不同曲率半径的透镜，其等厚干涉形成的圆环半径均随干涉级次k的增加而单调递增,且透镜曲率半径越大，干涉圆环半径增大趋势越明显；对于同一干涉级次，透镜曲率半径R越大，则干涉圆环半径r越大.

3 相邻干涉圆环间距的数值分析

从式(6)和式(7)可以看出，干涉圆环半径的表达式不是等差数列[7]，即干涉圆环半径r随干涉级次k的增大并非呈线性关系，图3也客观地证明了这一点.这表明相邻暗环或明纹间距并不相等，根据式(6)和式(7)，可得相邻暗环间距Δr和相邻明环间距Δr′分别为

Δr=rk+1-rk=

(8)

Δr′=rk+1-rk=

(9)

同样，式(8)和式(9)表明，牛顿环等厚干涉形成的相邻暗环或明环间距与入射光波长λ、透镜曲率半径R以及干涉级次k有关.同样以干涉暗环为例，通过理论计算，利用Origin软件绘图，分别在不同曲率半径下讨论干涉条纹间距的变化规律，如图4所示.

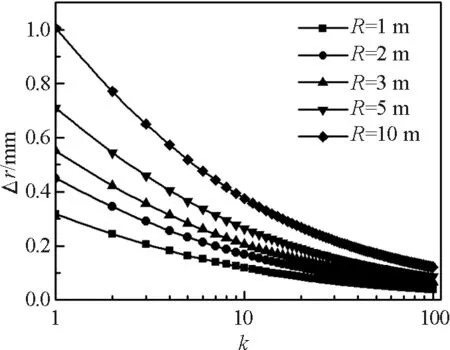
图4 不同R对应相邻干涉暗环间距随k的变化

由图4可知，对于不同曲率半径的透镜，其等厚干涉形成的相邻暗环间距均随干涉级次k的增加而单调递减；对于同一干涉级次，透镜曲率半径R越大，对应相邻干涉暗纹间距Δr也越大；当干涉级次较小时，透镜曲率半径越大则相邻暗环间距递减趋势越明显；当干涉级次较大时，相邻暗环间距基本趋于稳定，且不同曲率透镜下的圆环间距差别甚小.不难证明，对于牛顿环等厚干涉形成的明环，同样具有类似的规律.

4 结束语

通过数值分析，客观反映了牛顿环等厚干涉形成的条纹半径及相邻明、暗纹间距随干涉级次的变化规律，且均与平凸透镜的曲率半径有关.从本质上理清这种变化规律，有利于学生在学习时正确理解等厚干涉的原理及特点.