振荡浮子式双浮体波浪能装置的频域和时域分析

纪仁玮，张 亮，王树齐，朱仁庆

(1.哈尔滨工程大学 海洋可再生能源研究所，哈尔滨 150001;2.江苏科技大学 船舶与海洋工程学院，江苏 镇江 212001)

0 引 言

随着经济飞速发展，能源需求日益增长，化石燃料日渐枯竭，环境问题日益突出，开发和利用可再生能源迫在眉睫。波浪能作为一种环保、可再生、便于利用且储量丰富的新型能源,逐渐引起人们的重视[1-3]。波浪能的开采和利用主要通过波浪能发电装置来完成，其中振荡浮子式波浪能发电装置作为当前最具应用优势的波浪能装置之一，得到越来越多人的关注[4]。近年来，随着海洋资源开发逐渐从近海走向远海，波浪能装置已逐渐从单浮体发展为多浮体[5]。

国内外相关学者已在振荡浮子式波浪能装置研究方面做了大量工作。THOMAS等[6]研究波浪作用下单浮体的水动力特性和浮体间的相互干扰；ERIKSSON等[7]考虑线性脉冲串输出(Pluse Train Output,PTO)的影响，研究触底式圆柱型单浮体波浪能装置的水动力特性；BABARI等[8]通过黏性修正的方式考虑流体黏性对单浮体水动力性能的影响；NAZARI等[9]对单浮体进行研究，发现浮子的垂向位移受其固有频率和阻尼系数的影响较大；国威等[10]考虑非线性PTO的影响，研究单浮体波浪能装置的水动力特性。

综上所述，目前有关单浮体波浪能装置的研究较多，主要涉及水动力性能、运动特性和功率特性等，对双浮体波浪能装置的研究还处于探索阶段。对此，本文提出基于势流理论的ANSYS-AQWA方法，对振荡浮子式双浮体波浪能装置进行研究，主要包括：

1) 介绍多浮体频域和时域分析方法的基本理论；

2) 基于势流理论，通过AQWA软件对振荡双浮体波浪能装置进行模拟，采用Fortran对ANSYS-AQWA软件进行二次开发,在考虑PTO的影响的条件下得到双浮体波浪能装置振荡运动的数值计算结果，并将其与美国国家可再生能源实验室(NREL)的试验结果相对比；

3) 以特定的双浮体波浪能装置为研究对象，进行频域水动力和时域特性分析。

1 基本理论和计算方法

1.1 多浮体流场的基本理论

1.1.1 多浮体流场的速度势

流场中各浮体之间会相互影响，流场的速度势Φ可分为入射波势ΦI、绕射势ΦD和辐射势ΦR，每个浮体的辐射势都是自身的辐射势与其他浮体的辐射势的叠加。

若流场中存在N个浮体，则流场的总速度势为

(1)

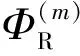
(2)

(3)

1.1.2 多浮体流场的水动力系数

基于线性伯努利方程，可得浮体的动压为

(4)

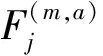
(5)

(6)

可得

(7)

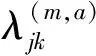
综上所述，第m个浮体受到的作用力为

(8)

1.2 浮体频域和时域计算方法

基于线性理论进行频域分析，浮体受到的力与运动位移呈线性关系，频域计算方法的关键是求解速度势。

1.2.1 速度势的求解

在浮体频域分析中，总速度势φ(x,y,z)由入射势φ0(x,y,z)、辐射势φj(x,y,z)(j=1，2，…，6)和绕射势φ7(x,y,z)构成。入射势φ0(x,y,z)已知，求解总速度势φ(x,y,z)的关键是对辐射势φj(x,y,z)(j=1，2，…，6)和绕射势φ7(x,y,z)进行求解[11]。

(9)

辐射势满足的控制方程和定解条件为

(10)

绕射势求解的控制方程和定解条件为

(11)

在已知入射势φ0(x,y,z)的情况下，通过求解式(10)和式(11)就可得到辐射势φj(x,y,z)和绕射势φ7(x,y,z)，从而求得流场中的总速度势φ(x,y,z)。

1.2.2 频域运动方程

浮体频域运动方程为

(12)

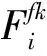
1.2.3 时域运动方程

采用时域计算方法可求得浮体受力与运动位移之间的非线性关系。常见的时域计算方法可分为直接法和间接法2种，其中间接法计算简单，应用较广。将浮体的运动看成一系列脉冲运动的叠加，将浮体受到的力看成一系列线性力的叠加，建立力与各时刻运动的关系，从而建立浮体运动方程，即

(13)

式(13)中：M为浮体的广义质量矩阵；λ为附加质量矩阵；K(t-τ)为系统的延迟函数；C为浮体结构的静水回复刚度；F(t)为浮体受到的广义力矩阵。借助快速傅里叶变换(Fast Fourier Transformation,FFT)将采用频域分析法得到的水动力系数转化为时域运动方程中的水动力参数。

1.2.4 双浮体波浪能装置的时域分析方法

本文基于势流理论，通过Fortran对ANSYS-AQWA软件进行二次开发，提出一套双浮体波浪能装置时域分析方法。采用该方法研究双浮体波浪能装置存在的技术难点，主要包括：浮子与浮筒之间的水动力干扰；垂荡阻尼板的影响[12]；浮子与浮筒之间PTO装置的影响。

2 双浮体波浪能装置的数值验证

2.1 模型的建立

双浮体波浪能装置由浮子和浮筒构成，其模型见图1，相关参数见表1。

a) 双浮体模型尺寸

b) 浮子网格示意

c) 浮筒网格示意

参数浮子浮筒质量/kg8.45×1041.65×105重心/m(0,0,-0.4)(0,0,-28.4)吃水/m1.6334.97

2.2 数值验证

垂荡运动是波浪能装置能发电的主要原因，本文仅考虑双浮体的垂荡运动，提出基于ANSYS-AQWA计算双浮体波浪能装置垂荡运动的方法。为验证该方法的正确性，选取波高为2.5 m的规则波，改变波浪周期，通过质量-弹簧-阻尼系统来模拟PTO。在PTO参数中,弹簧的刚度为20 kN/m，阻尼为1 200 kN·s/m，数值模拟的时间步长为0.5 s，计算总时间为500 s。

双浮体波浪能装置的数值模拟结果见表2，将其与文献[13]中的结果相对比，结果见图2。

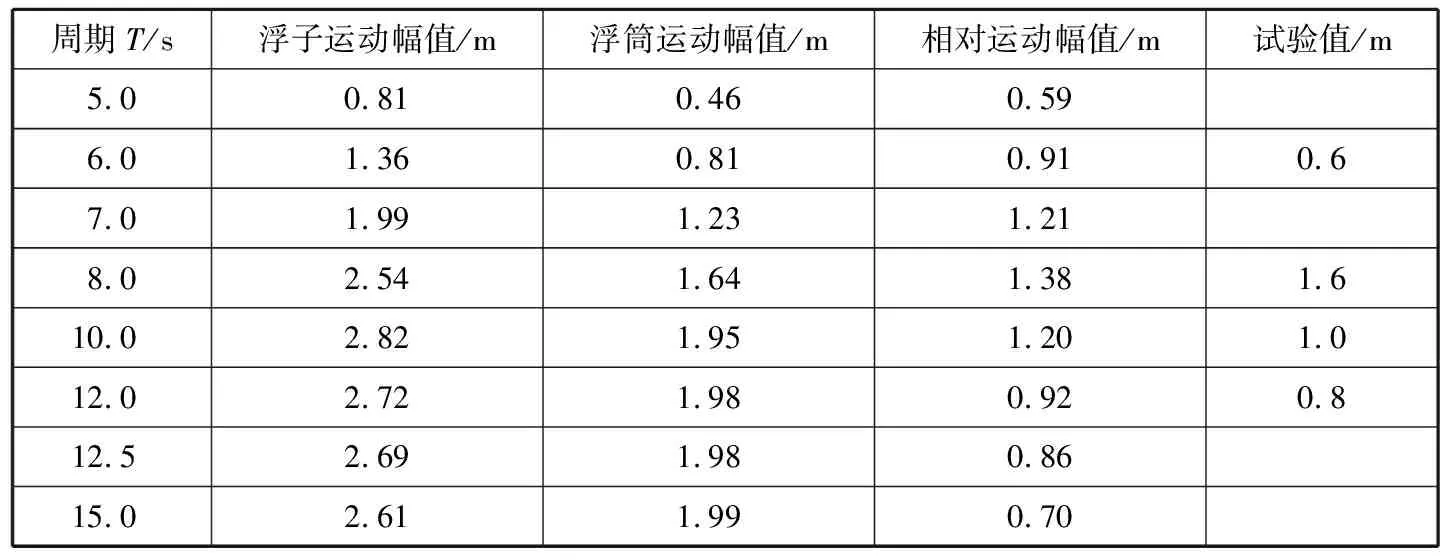
表2 双浮体波浪能装置的数值模拟结果

由图2可知，浮子与浮筒相对运动的数值模拟结果与试验结果吻合较好。当波浪周期为10 s时，浮子的垂荡运动幅值达到最大；浮筒的垂荡运动幅值随波浪周期的增大呈现“先增大后趋于平稳”的趋势，在垂荡过程中没有出现峰值；浮子与浮筒相对运动的幅值在波浪周期为8 s时达到最大。

发电功率是衡量波浪能装置性能的重要指标，选取5个波浪周期的瞬时功率的平均值作为波浪能装置的平均功率，瞬时功率可根据浮子和浮筒运动速度的时历曲线来确定。图3为不同PTO阻尼系数下双浮体波浪能装置的功率随波浪周期的变化。由图3可知：当阻尼系数为1 200 kN·m/s时，除了共振周期以外，AQWA数值计算结果与试验结果吻合较好，共振周期处的误差主要是忽略黏性效应和试验误差导致的；不同阻尼系数对应不同的共振周期和最优吸收功率。

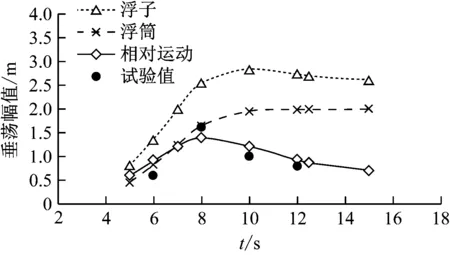
图2 不同波浪周期下双浮体波浪能装置数值模拟结果与试验结果的对比

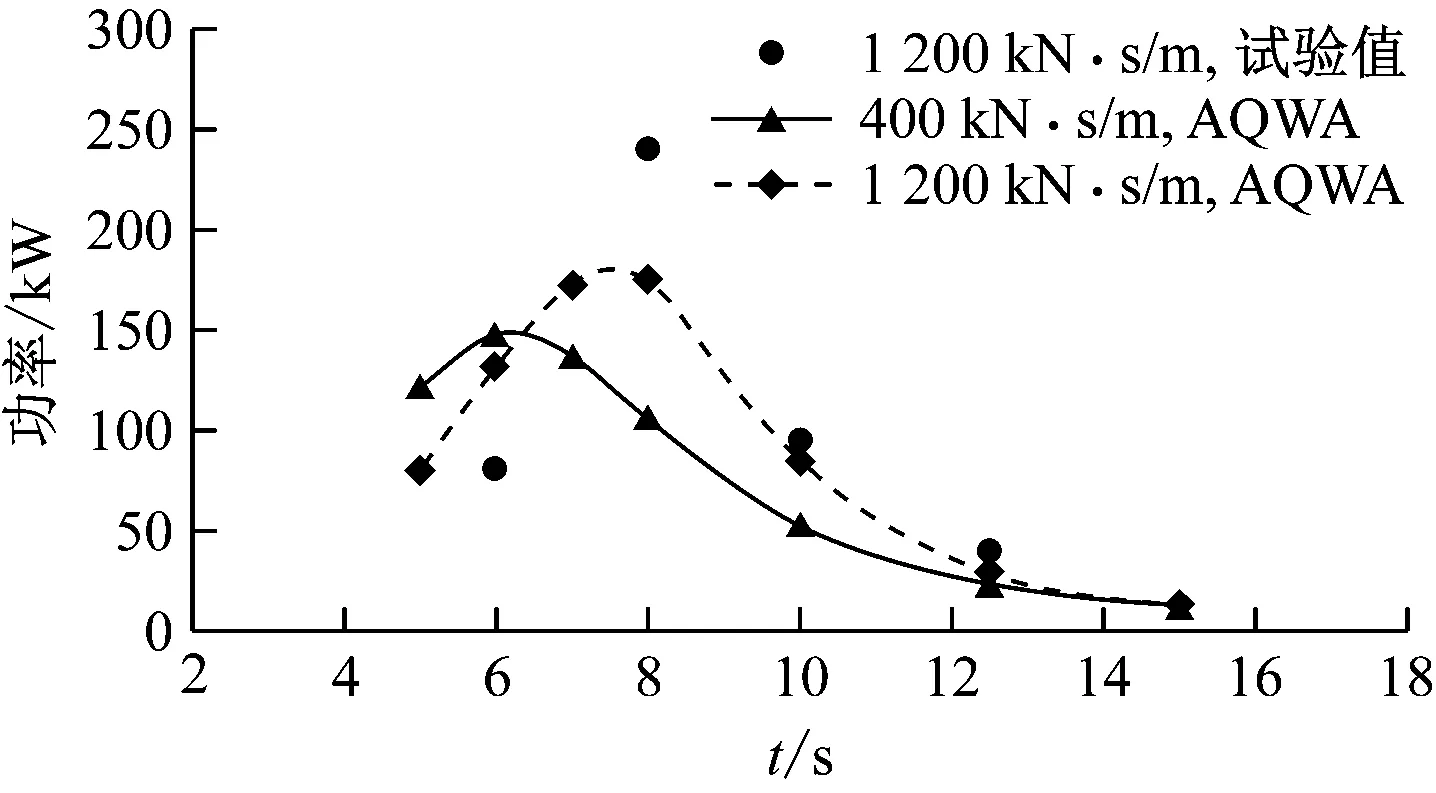
图3 不同PTO阻尼系数下双浮体波浪能装置的功率随波浪周期的变化

3 频域水动力分析

3.1 浮子和浮筒的水动力系数

3.1.1 垂向波浪载荷

图4为双浮体波浪能装置垂荡时浮子和浮筒的垂向波浪力。由图4可知：浮子的垂向波浪力远大于浮筒；浮子的垂向波浪力与波浪频率呈负相关关系，且减缓的速度逐渐变慢；浮筒的垂向波浪力随波浪频率先增大后减小，约在频率为0.65 rad/s时达到峰值。

图4 双浮体波浪能装置垂荡时浮子和浮筒的垂向波浪力

3.1.2 辐射阻尼系数

图5为垂荡运动辐射阻尼系数。由图5可知：浮筒垂荡的辐射阻尼系数的数量级比浮子小很多；浮子和浮筒的辐射阻尼系数均随波浪频率呈“先增大后减小再趋于平稳”的趋势，但达到最大值的频率有所不同。

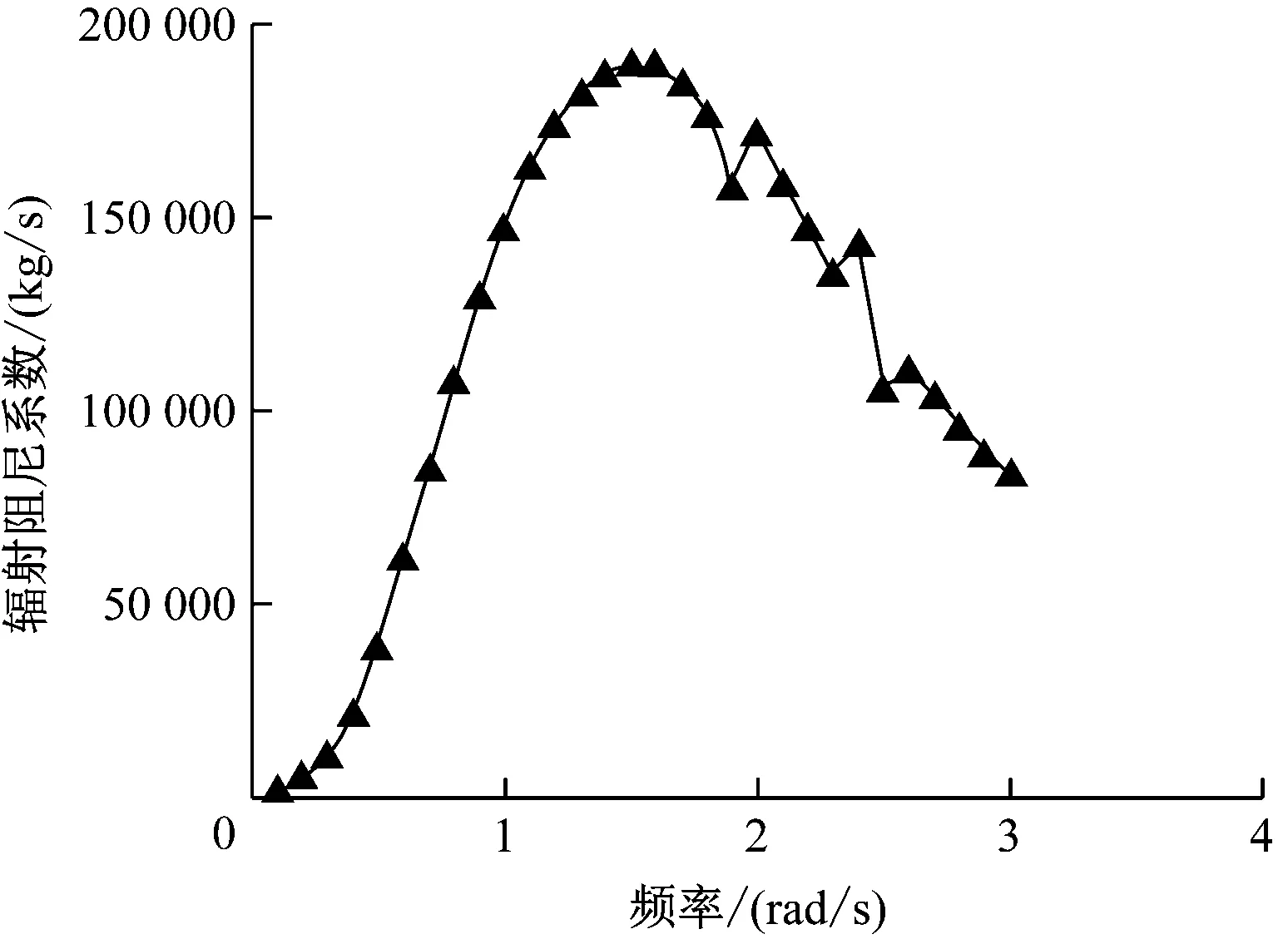
a) 浮子垂荡的辐射阻尼系数

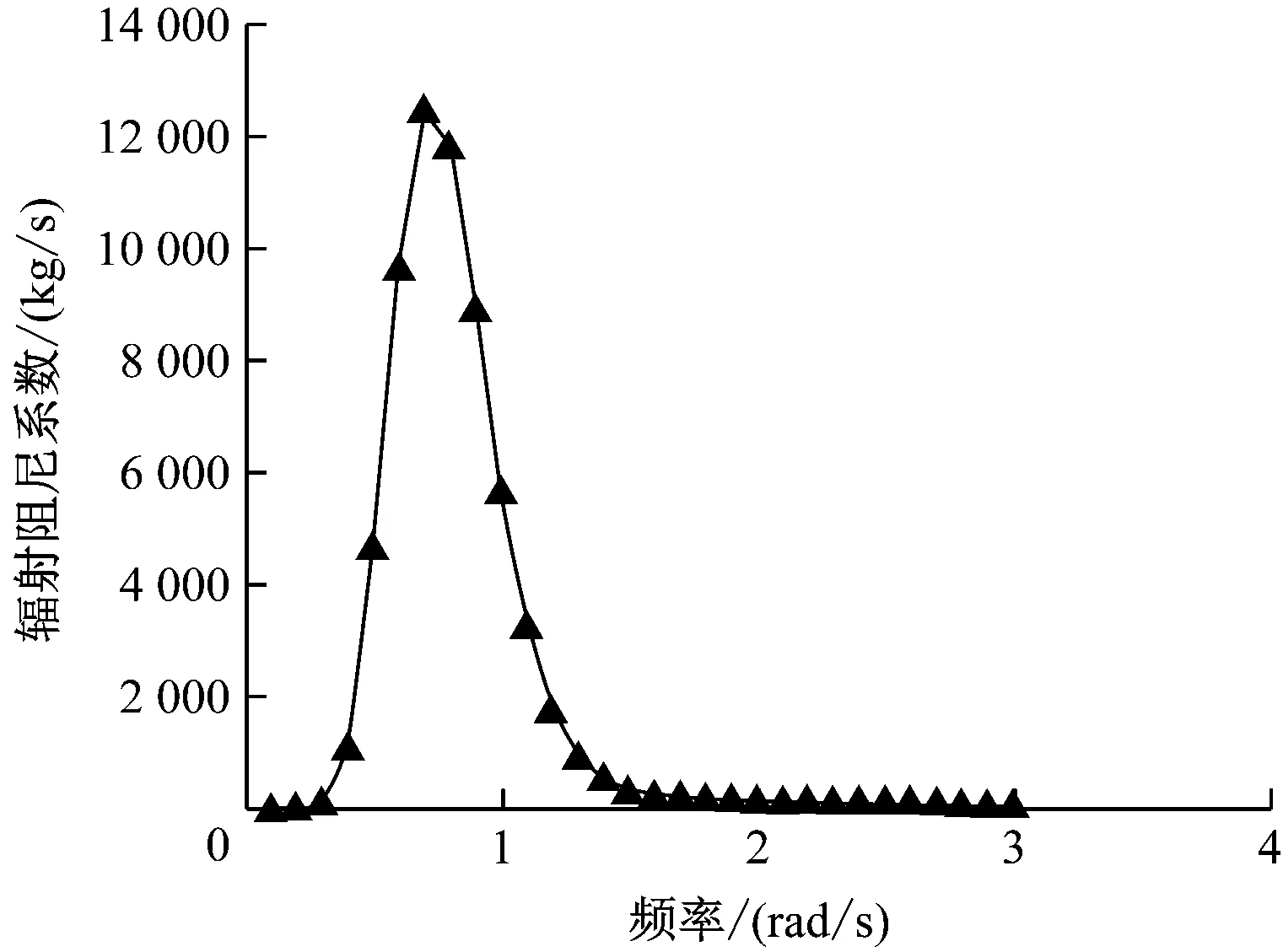
b) 浮筒垂荡的辐射阻尼系数

3.1.3 附加质量系数

图6为垂荡附加质量。由图6可知：浮子和浮筒的垂荡附加质量在同一个量级上，但浮子的附加质量较小；浮子的垂荡附加质量随频率的增大先逐渐减小后趋于平稳，但仍在1个量级内变化；浮筒的垂荡附加质量随频率呈现出1个峰值和1个谷值，但总体变化范围较小。这是由于浮筒的排水体积较大，吃水较深，波浪在自由液面以下对浮体的作用力要小于在自由液面处对浮体的作用力。

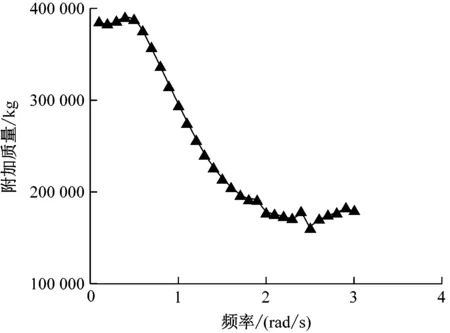
a) 浮子垂荡附加质量

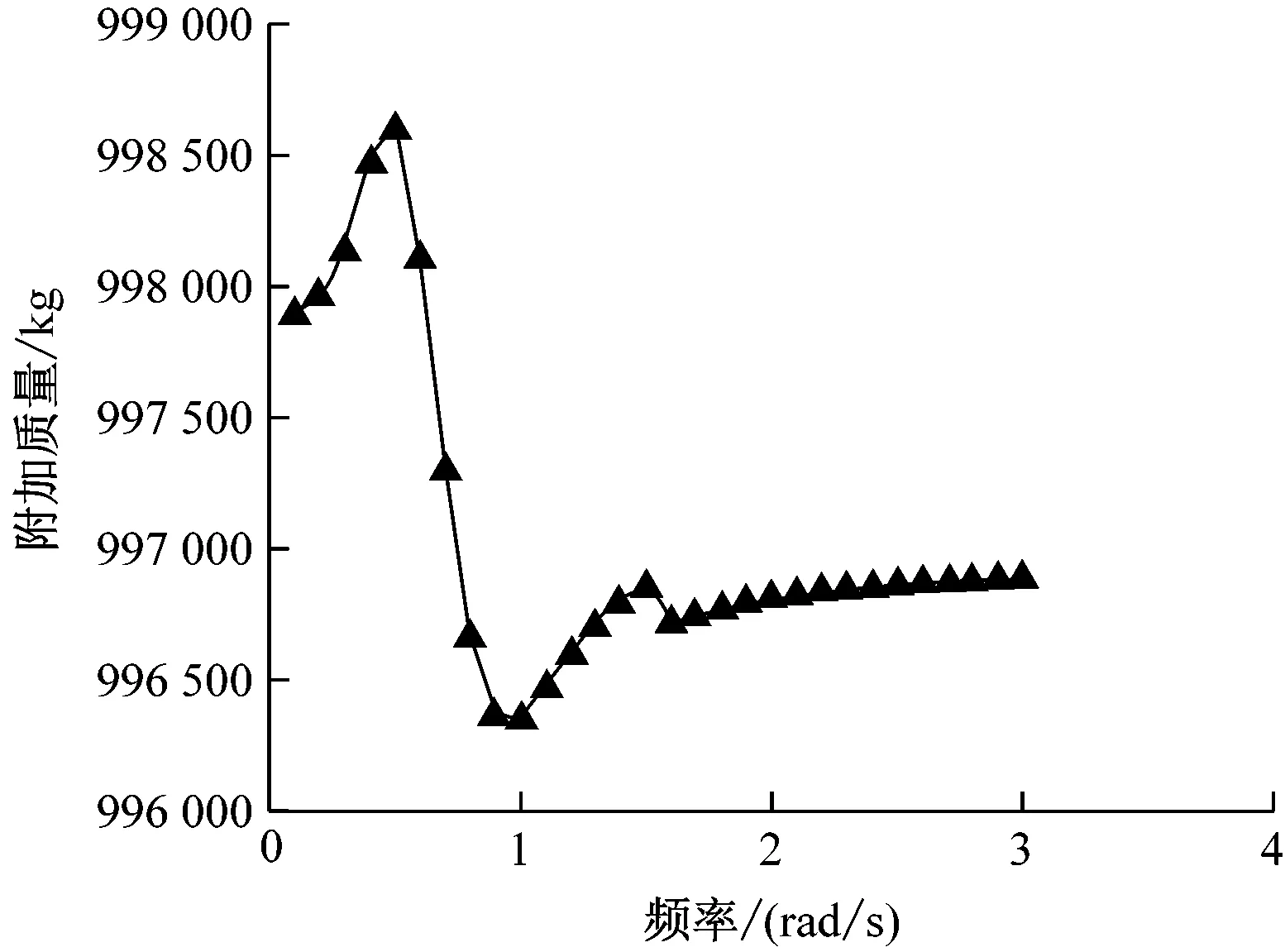
b) 浮筒垂荡附加质量

3.1.4 浮子与浮筒的相互影响

在双浮体波浪能装置工作期间，需考虑浮子与浮筒的相互干扰。在任意一个浮体的波浪力中，必须考虑另一个浮体垂荡运动产生的辐射势影响，即考虑另一个浮体垂荡运动对应的附加质量和辐射阻尼系数的影响。

图7和图8分别为浮子与浮筒相互影响的垂荡附加质量和垂荡辐射阻尼。由图7和图8可知：在附加质量和辐射阻尼方面，双浮体之间相互影响的规律基本一致；附加质量随频率变化的范围较大，在低频区域出现负值；辐射阻尼均在负值范围内变化，呈现“先减小后增大”的趋势。

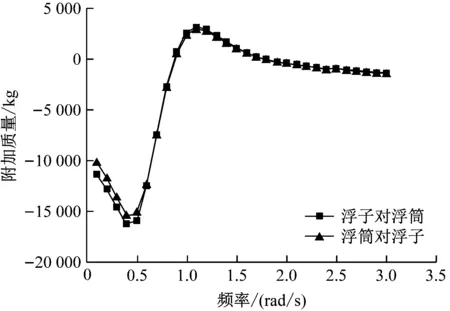
图7 浮子与浮筒相互影响的垂荡附加质量

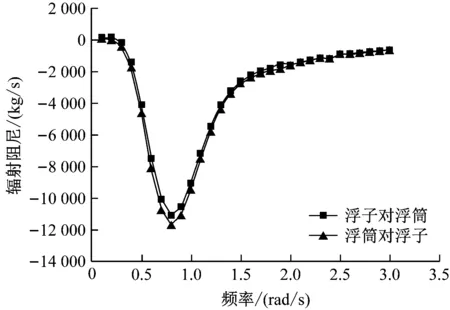
图8 浮子与浮筒相互影响的垂荡辐射阻尼

3.2 浮子和浮筒的运动响应

在运动响应方面，考虑“自由状态”和“约束状态”2种情况。浮子和浮筒在垂荡运动下，其“自由状态”不考虑PTO装置的外部阻尼对运动响应的影响，“约束状态”考虑PTO装置的影响。

选取单位波幅规则波，得到自由状态下浮子和浮筒的垂荡运动响应见图9。由图9可知：浮子的垂荡RAO在低频阶段(0～1.6 rad/s)保持不变，在高频阶段(1.6～3.0 rad/s)逐渐减小，且减小速度逐渐变慢；浮筒的垂荡RAO主要体现在低频阶段(0～1.1 rad/s)，在高频阶段(1.1～3.0 rad/s)较小且保持不变。图10为约束状态下浮子和浮筒的运动响应。由图10可知：由于PTO装置的存在，浮子和浮筒的垂荡RAO与图9相比均发生明显的变化，呈现出“先增大后减小”的趋势，在0.75 rad/s附近达到最大值；浮子与浮筒的相对运动呈现出相同的规律，但垂荡RAO峰值对应的频率变大，约为0.8 rad/s，对能量获取有重要意义。

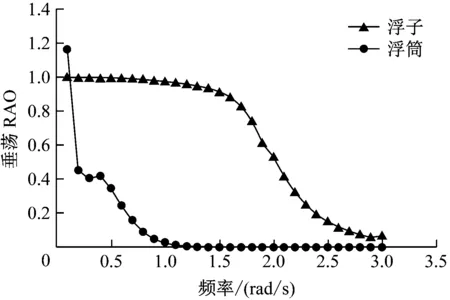
图9 自由状态下浮子和浮筒的垂荡运动响应

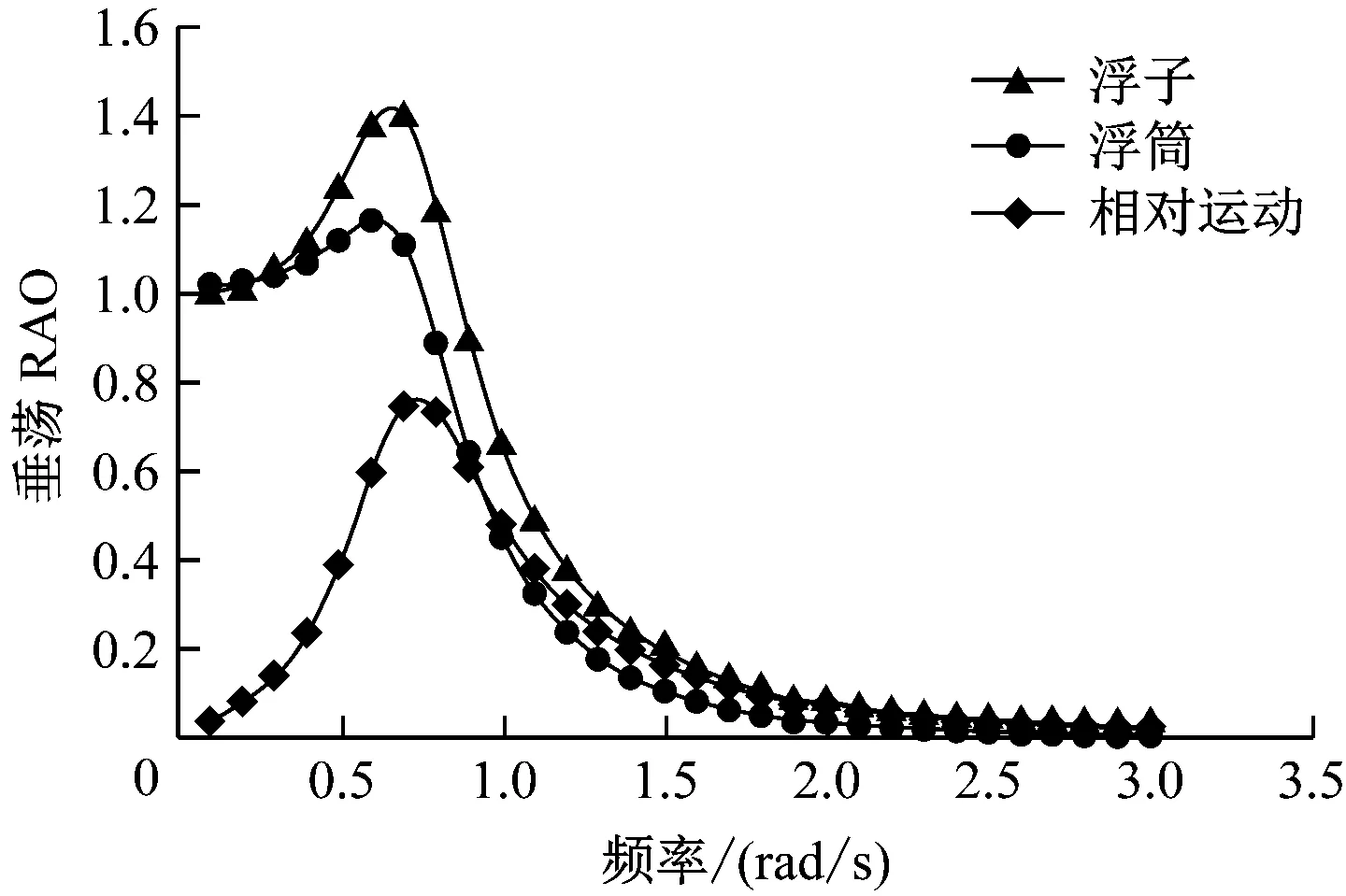
图10 约束状态下浮子和浮筒的运动响应

4 时域特性分析

通过Fortran语言对AQWA软件进行二次开发，以外力的形式考虑浮子与浮筒之间因PTO装置存在而产生的相互影响，并调用频域水动力计算结果，分析波浪能装置在规则波和不规则波下的时域运动特性。

4.1 装置在规则波下的运动特性

表3为双浮体波浪能装置在规则波下的计算参数，图11～图14为浮子和浮筒在垂荡状态下的F-K力、绕射力、位移和速度。由图11～图14可知：在规则波的作用下，浮子和浮筒在垂荡状态下的F-K力、绕射力、位移和速度均呈现周期性变化，且存在相位差；浮子在垂荡状态下的F-K力远大于浮筒，由于浮子的直径较大，湿表面远大于浮筒；浮子在垂荡状态下的绕射力大于浮筒，但二者仍在同一量级；浮子在垂荡状态下的位移和速度幅值均大于浮筒。

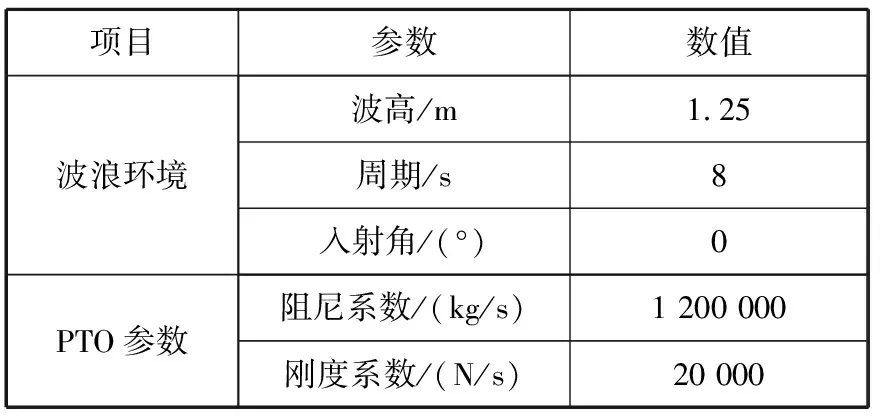
表3 双浮体波浪能装置在规则波下的计算参数

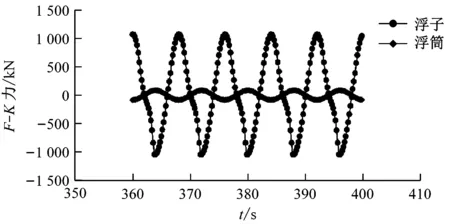
图11 垂荡状态下浮子和浮筒的F-K力

图12 垂荡状态下浮子和浮筒的绕射力

图13 垂荡状态下浮子和浮筒的位移

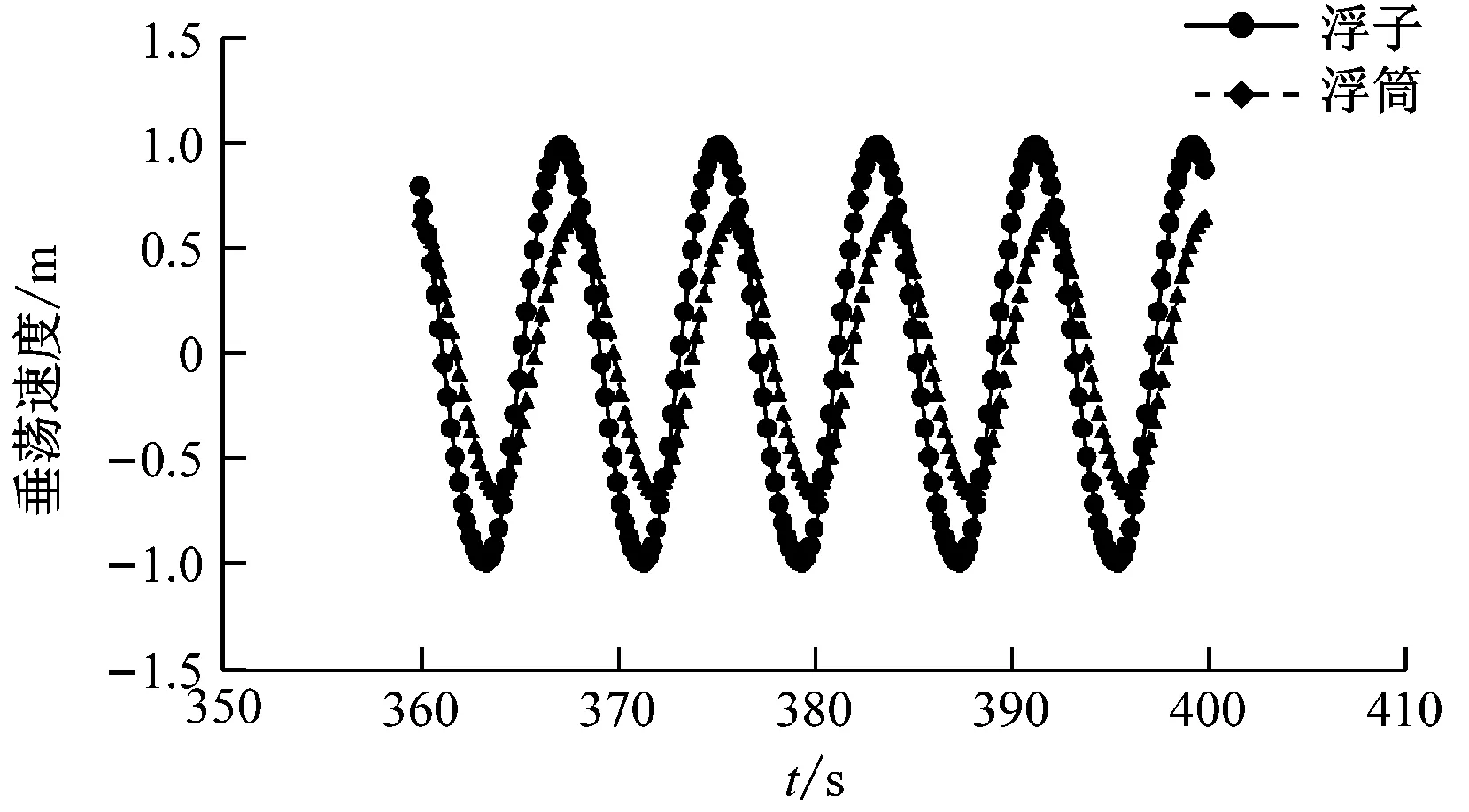
图14 垂荡状态下浮子和浮筒的速度

4.2 装置在不规则波下的运动特性

进一步研究双浮体波浪能装置在不规则波作用下的时域运动特性，不规则波通过波浪谱来描述，常见的波浪谱有Neumann谱、ITTC谱、P-M谱和JONSWAP谱等。不规则波的方向为0°，采用P-M谱，谱参数见表4，其波谱表达式为

(14)

式(14)中：g为重力加速度；ω为波浪频率;U为距离海平面19.5 m处的风速。

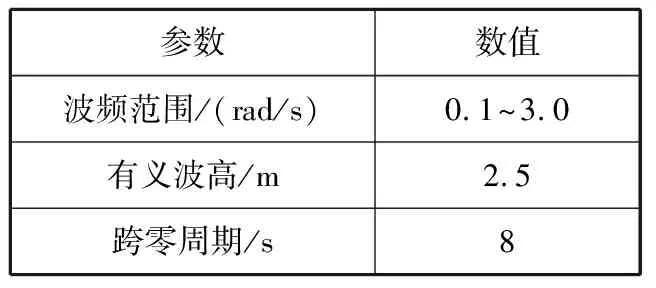
表4 P-M谱参数

图15～图18分别为浮子和浮筒在垂荡状态下的绕射力、辐射力、位移和速度时域曲线。由图15～图18可知：由于不规则波的周期和波高时刻在变化，导致浮子和浮筒在垂荡运动下的绕射力、辐射力、位移和速度均呈无规律的变化趋势。

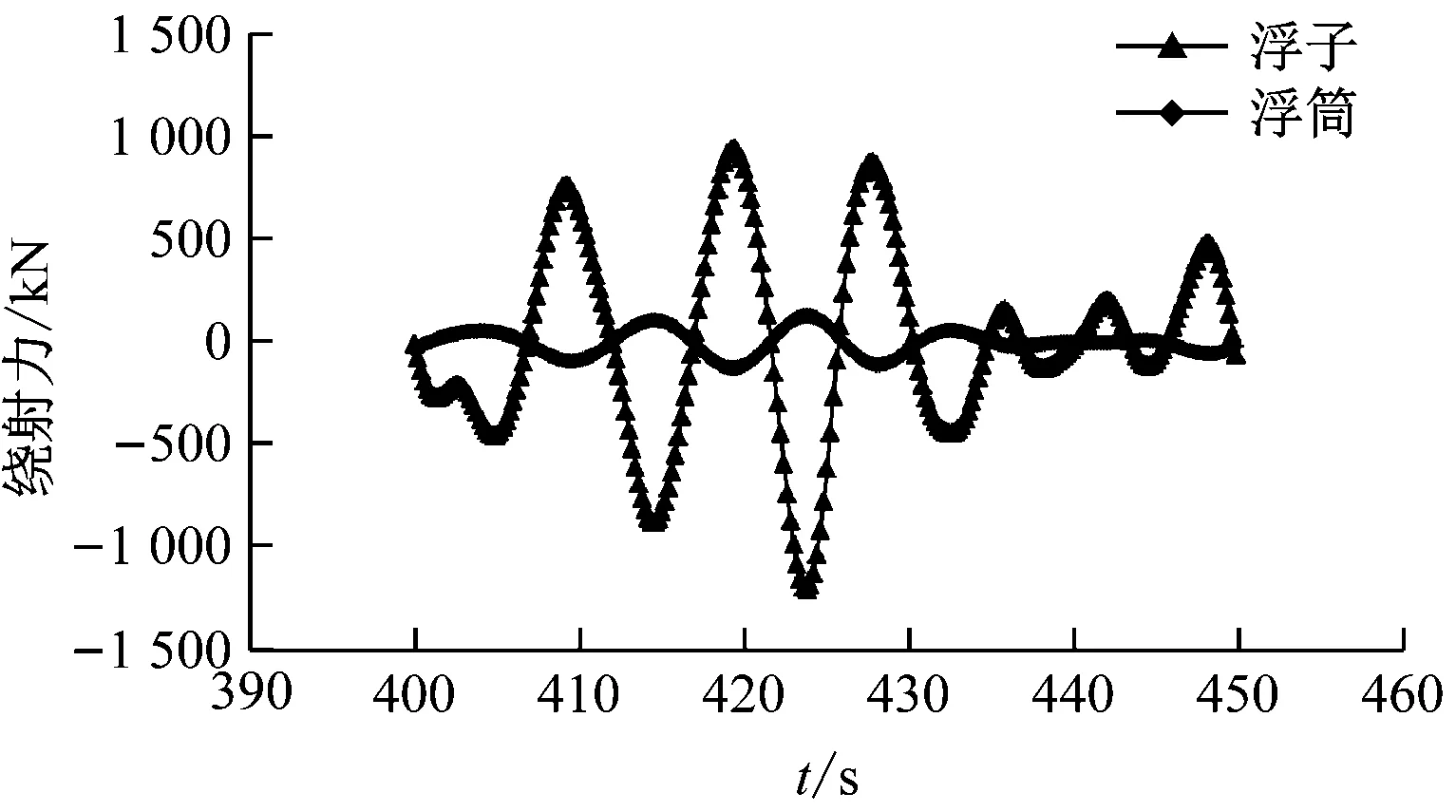
图15 垂荡状态下浮子和浮筒的绕射力时域曲线

图16 垂荡状态下浮子和浮筒的辐射力时域曲线

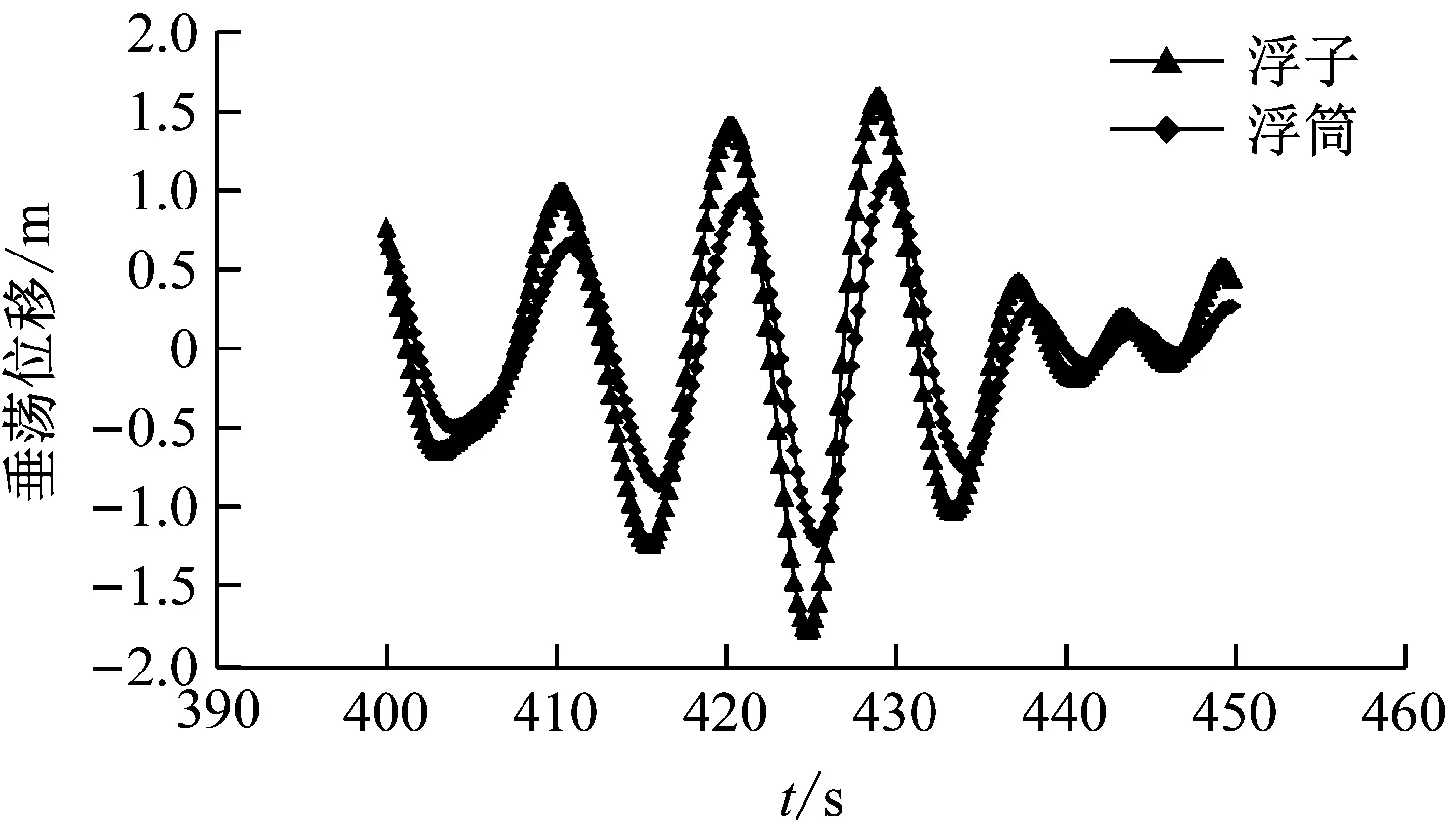
图17 垂荡状态下浮子和浮筒的位移时域曲线

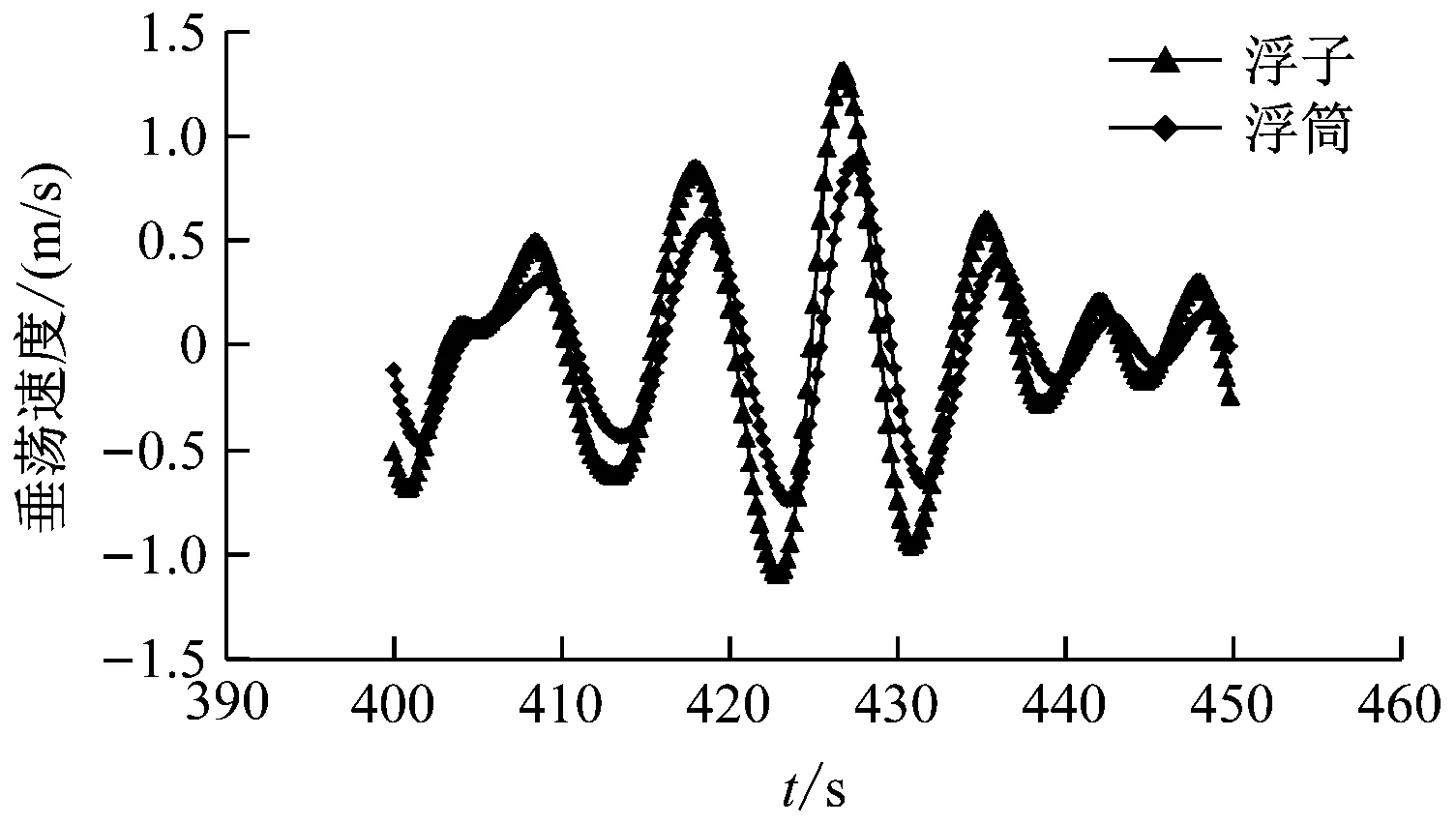
图18 垂荡状态下浮子和浮筒的速度时域曲线

有义波高是P-M波浪谱的重要参数，对波浪能装置的运动特性有很大影响，取有义波高分别为2 m、3 m和4 m，研究有义波高对波能发电装置运动特性的影响。

图19为不同有义波高下浮子和浮筒相对垂荡速度时域曲线。由图19可知：在不同有义波高下，浮子和浮筒相对垂荡运动的变化趋势相同；相对垂荡运动的峰值随着有义波高的增大而增大，说明有义波高较大有利于波能装置进行能量转化。

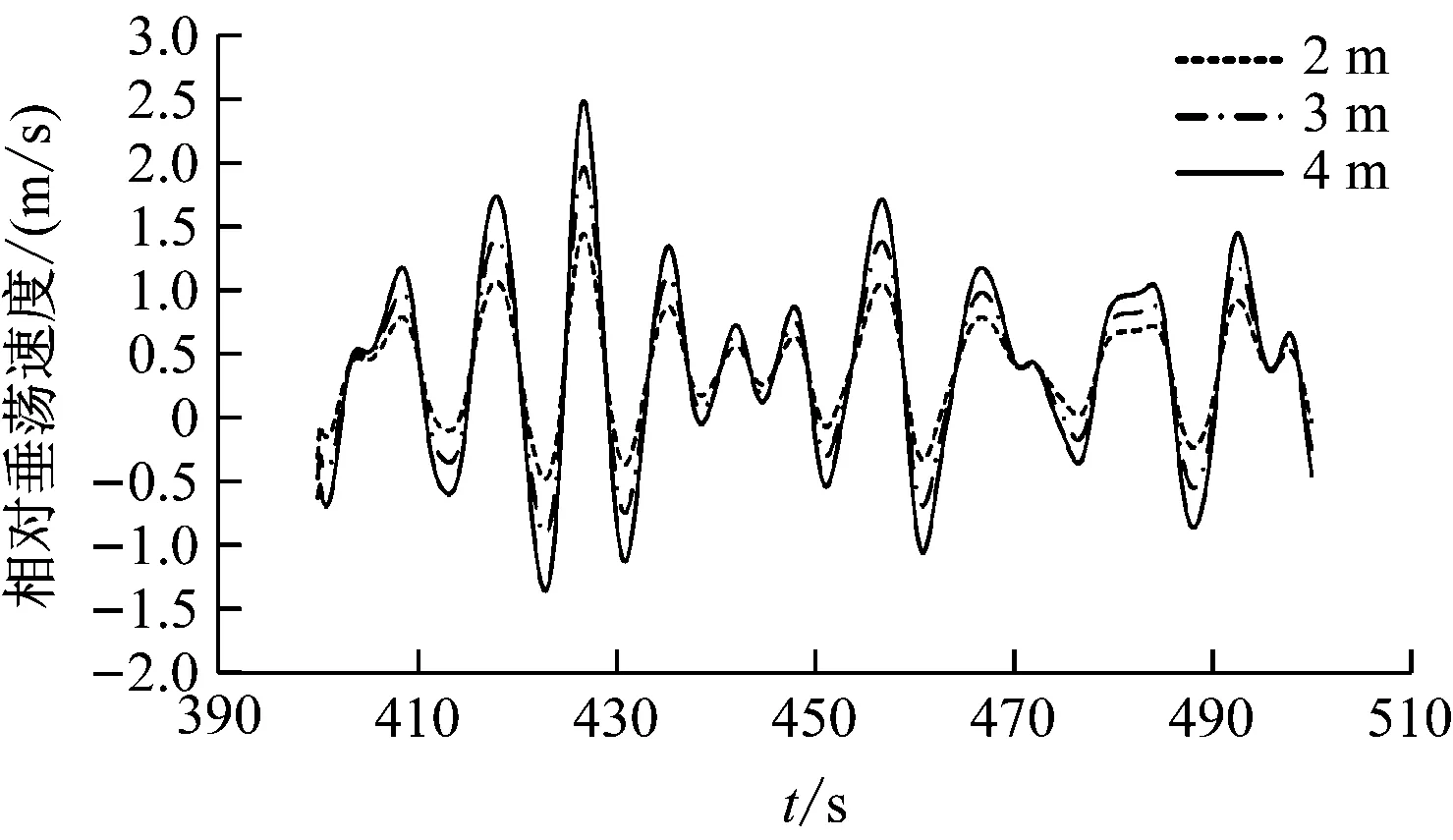
图19 不同有义波高下浮子和浮筒相对垂荡速度时域曲线

5 结 语

本文介绍了双浮体波浪能装置的基本理论，提出了基于ANSYS-AQWA研究振荡浮子式双浮体波浪能装置运动的方法，并对计算结果和NREL的双浮体波浪能装置试验结果进行了对比，证明了该方法的可行性。此外，分析了双浮体波浪能装置的频域水动力性能，以及在规则波和不规则波下的时域运动响应。研究结果表明：

1) 不同的PTO阻尼系数对应着不同的共振周期和最优吸收功率；

2) 对于双浮体波浪能装置而言，浮子与浮筒之间水动力的相互影响呈现出相同的变化趋势；

3) 在规则波的作用下，浮子和浮筒在垂荡运动下的F-K力、绕射力、位移和速度均呈现周期性变化，变化周期为入射波的周期，且浮子的运动响应大于浮筒；

4) 在不规则波作用下，垂荡运动呈现出不规则的变化趋势，增大有义波高有利于波浪能装置进行能量转化。