轮毂电机驱动纯电动汽车的车体侧偏角观测与稳定性控制

耿 聪，张 欣，姜 涛，张 健

(北京交通大学 机械与电子控制工程学院，北京 100044)

轮毂电机驱动纯电动汽车具有转矩易测量且控制精度高的特点，更加容易实现极限驱动状态下的主动安全控制，有利于提高电动汽车的稳定性[1-3].

当前，国内外学者对于轮毂电机驱动电动汽车转矩分配策略，根据控制目标的不同，主要分为基于横摆角速度控制的转矩分配策略和基于横摆角速度与质心侧偏角联合控制的转矩分配策略[4-5].

基于横摆角速度反馈控制的转矩分配策略研究方面，文献[6-8]分别采用PI控制、模糊控制及神经网络控制算法，利用差动驱动/制动的转矩协调控制策略将转矩分配到四个车轮，实现车辆直接横摆控制(Direct Yaw-moment Control，DYC).这种转矩控制策略能够较好的控制横摆角速度，但是必须保证车辆质心侧偏角较小时才能起到很好的操纵稳定性控制效果，由于没有质心侧偏角反馈及未充分考虑轮胎非线性特性，会造成车辆在高速行驶时质心侧偏角过大的问题，不适用于质心侧偏角较大时的操纵稳定性控制.基于横摆角速度与质心侧偏角联合控制方面，文献[9-10]分别采用了线性二次调节器(Linear Quadratic Regulator，LQR)控制与滑模控制算法.横摆角速度及质心侧偏角得到较好控制，但转矩分配控制策略并未充分考虑轮胎的非线性特性，极限工况侧偏角观测误差较大，无法实现车辆横摆控制.

本文作者提出一种基于模型跟踪和最优控制的DYC方法.使用二自由度线性模型得到车辆运动状态参数，利用车体侧偏角β和横摆角速度γ描述车辆的理想响应.通过模型跟踪控制，对实际响应与理想响应误差进行反馈控制，得到车辆横摆力矩N的最优控制决策.反馈控制需要车辆的实际状态值，但是车体侧偏角β的直接测量方式相对昂贵，因此需要根据可测参数包括横摆角速度γ以及车体的侧向加速度ay等估算得到β值，即构造β观测器.为解决β观测器设计中车辆的非线性特性问题，提出了一种基于非线性轮胎模型的等效线性观测器设计方法.通过非线性轮胎模型精确描述了车辆的动力学特性，提出了扩展轮胎侧偏刚度参数的概念，构造了等效线性二自由度模型，从而通过采用线性控制器设计方法解决了非线性观测的问题.

1 车体侧偏角β观测器

1.1 β观测器设计

观测器的算法结构如图1所示，通过状态方程的预测值及输出方程的校正值得到的车体偏侧角β的估计值.

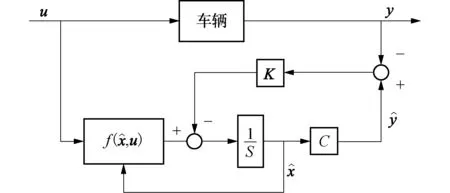
图1 采用非线性轮胎模型的β观测器算法结构Fig.1β observer with nonlinear tire model

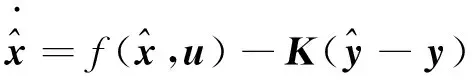
(1)

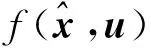
观测器的状态变量、输入变量和输出变量分别为

(2)

式中：δf为前轮转向角；ay为车体的侧向加速度；N为由左右轮胎纵向力差值所形成的直接横摆力矩；γ为横摆角速度.

观测器的输出方程为

(3)

轮胎的非线性侧偏力学特性为[11]

(4)

式中：Fyi为各轮胎侧向力；αi为各轮胎侧偏角；Ci为各轮胎侧偏刚度值；Fzi为各车轮垂直载荷；μ为路面摩擦系数；kxi为各轮胎的纵向力影响因素；i为各轮胎的标号.

与线性轮胎模型相比，非线性轮胎模型可描述轮胎在大侧偏角条件下的饱和特性，同时可反映轮胎垂直载荷、纵向力及路面摩擦系数的影响.采用二自由度车辆模型作为观测器模型，如图2所示.车辆的动力学方程为[11]

(5)

式中：m是车辆质量；Iz车辆的横摆转动惯量；lf为车辆质心到前轴的距离；lr为车辆质心到后轴的距离；Fxf为前轮纵向力；Fyf为前轮侧向力；Fyr为后轮侧向力.

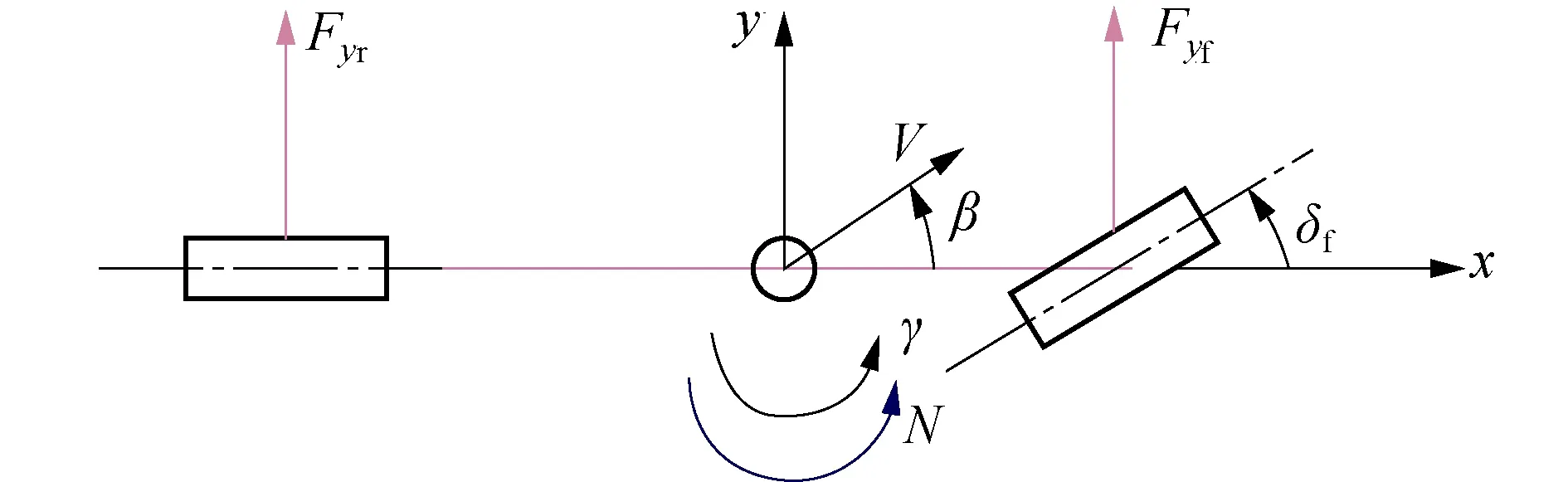
图2 用于观测器设计的二自由度车辆模型Fig.2 Two-degree of freedom vehicle model for observer design

由于高速行驶下δf值较小，观测器的非线性状态方程可描述为

(6)

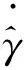
非线性观测器的设计和应用比较困难，所以利用线性控制器设计方法解决非线性问题.通过定义扩展轮胎侧偏刚度值Cp′，将非线性观测器模型转换为等效线性二自由度模型.Cp′的定义为

Cp′=Fy/α

(7)

式中：Fy为轮胎在运行工作点的侧向力；α为轮胎在运行工作点的侧偏角.

通过各运动学变量及运动学关系式得到α，通过非线性轮胎模型计算得到Fy，从而实时更新Cp′值[12].通过定义Cp′，非线性轮胎模型在运行点处的等效线性模型可描述为[13]

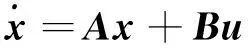
(8)

式中：A为状态方程的系统矩阵；B为状态方程的输入矩阵.

等效线性模型与参考文献[12]中的线性观测器具有相同的结构，因此可采用相同的设计方法构造反馈矩阵K.根据参考文献[13]，以提高观测器的鲁棒性和适应性为目标，反馈矩阵K为

(9)

式中：λ1、λ2为观测器极点值；Cfl′、Cfr′、Crr′、Crl′为4个车轮的扩展轮胎侧偏刚度.

在该观测器的构造中，将非线性轮胎模型及反馈矩阵的鲁棒算法相结合，可充分提高侧偏角观测的精度、响应速度及工况适应性.

1.2 β观测器的实验研究

为验证提出的β观测器构造方法，使用轮毂电机驱动电动汽车进行了实车实验，如图3所示.车辆装配了加速度传感器ADXL202，横摆角速度传感器HOFG-CLI(A)以及非接触光学测速仪CORREVIT S-400，用于获得测量车辆的ay,γ和β.

图3β观测器的实车路面实验Fig.3 Road test of βobserver

实验中，方向盘转角输入采取阶跃输入方式，路面条件为干燥柏油路面，附着条件良好，见图4.

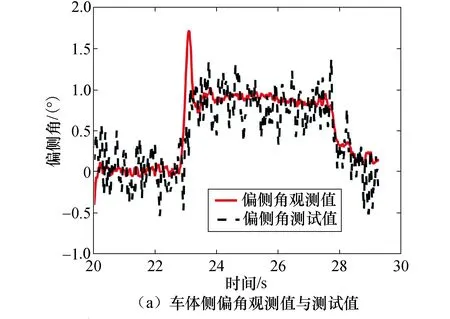
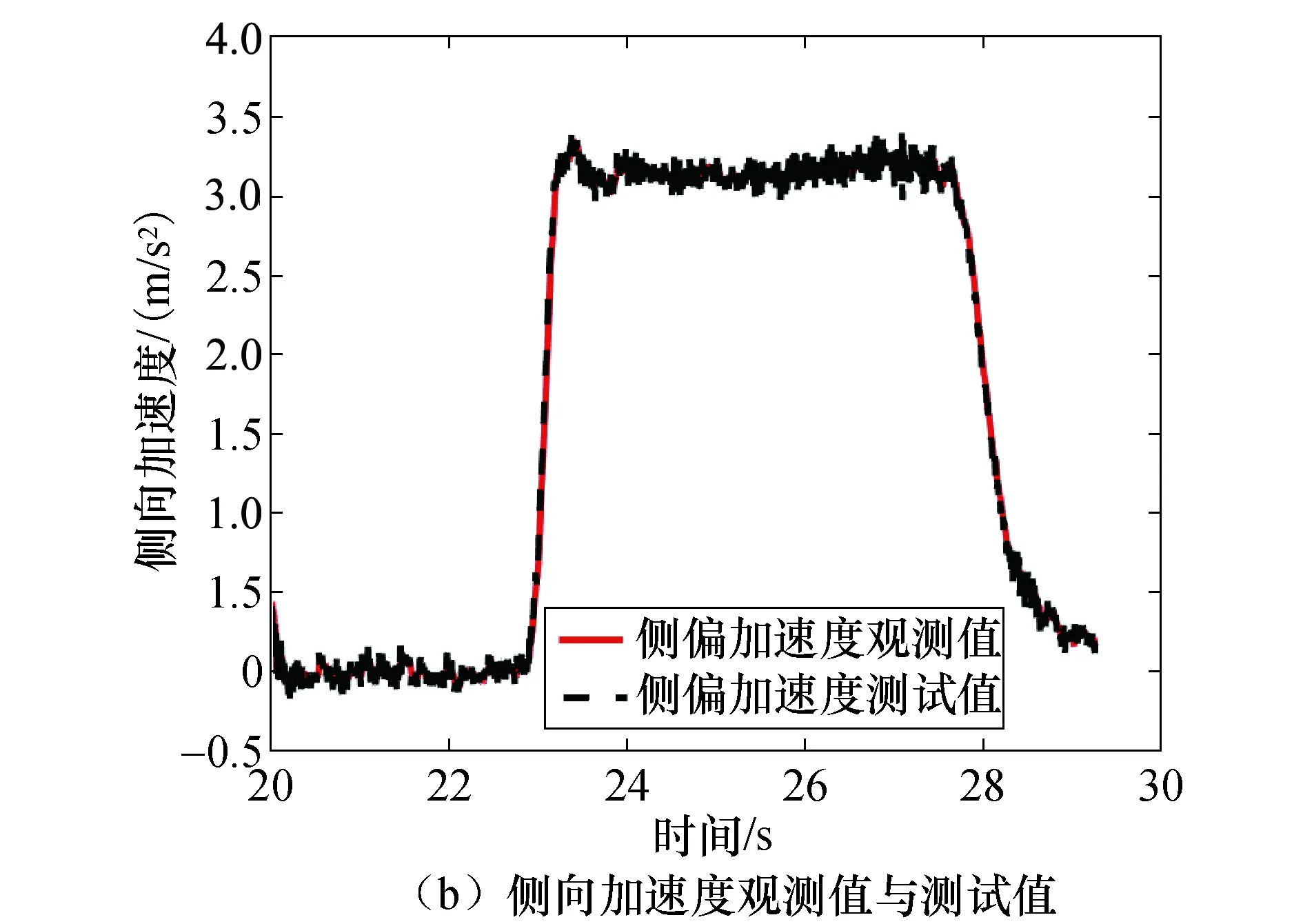
图4 车速40 km/h时实验结果Fig.4 Experimental results at a speed of 40 km/h

车速为40 km/h，方向盘转向角为90°时，由于车速较低，车体侧向加速度较低，车辆及轮胎的动力学特性基本处于线性状态，车体侧偏角和侧向加速度的观测值与测试值变化趋势一致，较为接近.

如图5所示，车速为60 km/h，方向盘转向角为90°时，由于车速的提高，车体侧向加速度较高，车辆及轮胎的动力学特性已进入非线性运行状态.在非线性运行区，车体侧偏角及侧向加速度的观测值同样与测试值变化趋势一致且比较接近.从实验结果可知，提出的等效线性观测器在车辆的线性运行区和非线性运行区都是有效的，两种实验状态都可以获得满意的侧偏角观测效果.

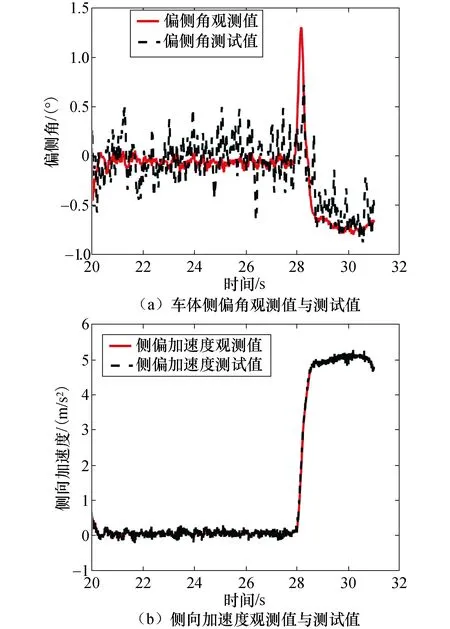
图5 车速60 km/h实验结果Fig.5 Experimental results at a speed of 60 km/h

2 基于侧偏角反馈的车辆稳定性控制

2.1 理想响应模型和状态误差方程

由线性二自由度模型得到的理想响应为

(10)

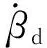
理想响应状态Xd和实际响应状态X的状态误差E为

(11)

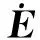
(12)

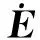
2.2 基于β误差变权重的直接横摆力矩最优决策

基于LQR的控制方法，通过状态误差反馈得到横摆力矩N*为

N*=-k1(β-βd)-k2(γ-γd)

(13)

式中：反馈系数k1和k2由代价函数J确定.代价函数J为

(14)

式中：q1、q2为状态误差的权重系数；Δβ为车体侧偏角的控制偏差；Δγ为横摆角速度的控制偏差.

为确定q1和q2，引入系数车体侧偏角权重ωβ(0≤ωβ≤1)来描述对β偏差的权重.定义q1=q2ωβ、q2=q2(1-ωβ)，式中q为车辆状态误差与横摆力矩控制间的权重系数.代价函数可表示为

N(t)]dt

(15)

为获得高的车辆稳定性，当β误差较小时,γ的跟踪控制较为重要，并且随着β误差增大，γ控制变得更为重要.此外，低摩擦系数路面条件下的车辆稳定性对β误差比高摩擦系数路面下更敏感.因此，ωβ的值为

(16)

式中：β0为控制参数，限定值为10°；|β|为车体侧偏角绝对值.

ωβ是根据|β|进行调整，如图6所示.在|β|的绝对值到达设定的μβ0前，式(16)中的ωβ是随车体侧偏角绝对值|β|绝对值数值的增加而线性增加的，其斜率为1/μβ0.当|β|的绝对值到达设定的μβ0，ωβ达到最大值1，|β|绝对值大于μβ0后，ωβ保持在最大值1.

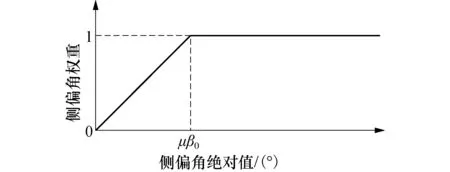
图6 侧偏角偏差权重Fig.6 Weight of sideslip angle deviation

2.3 基于β反馈的稳定性控制仿真结果

路面摩擦系数为0.2、车速为30 m/s、转向角正弦输入时的车辆状态响应特性如图7所示.有β控制时车辆横摆角速度曲线与理想曲线较为接近，车体侧偏角被控制在合理范围之内，车辆稳定性得到有效控制，无β控制时横摆角速度过大，车辆发生失控.

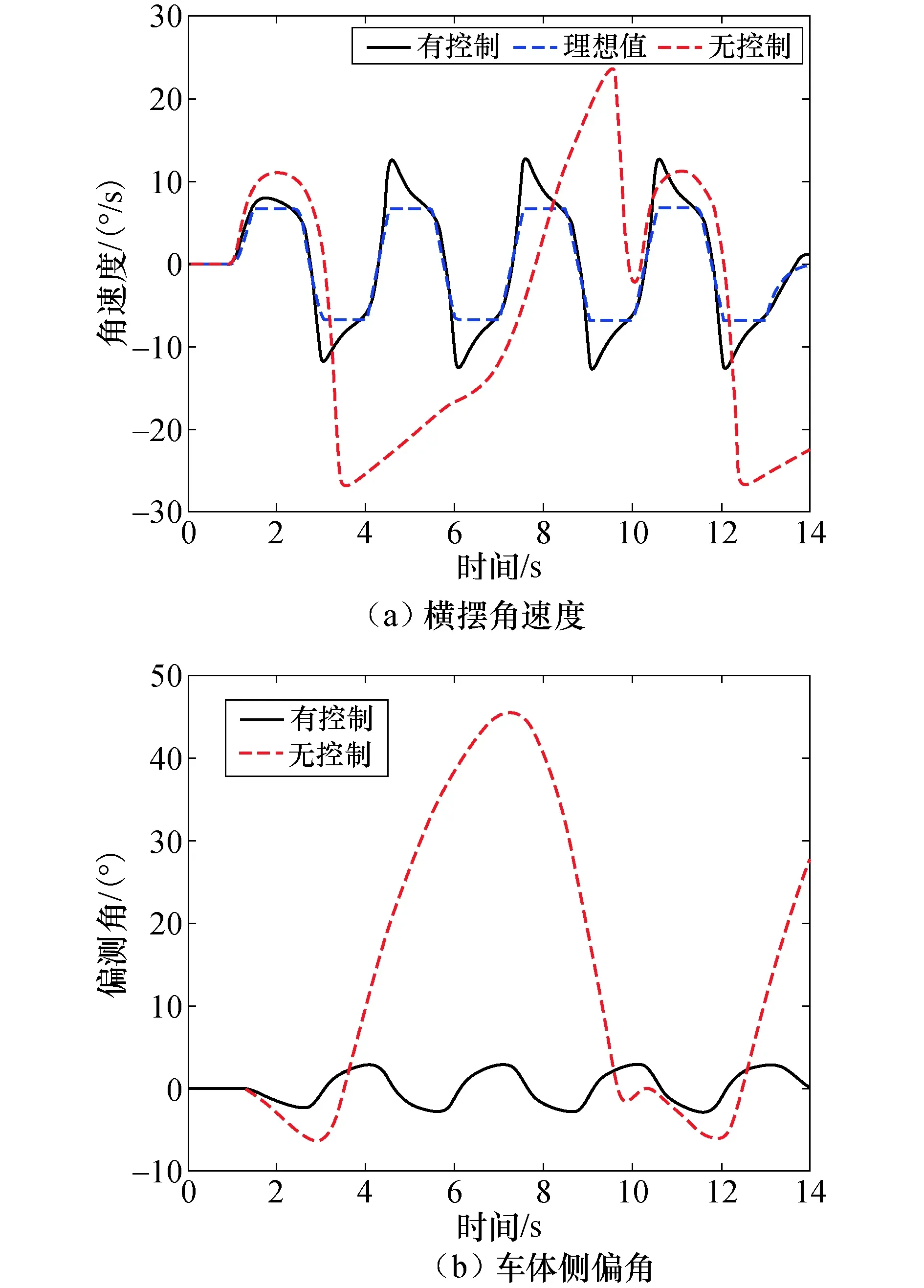
图7β控制的仿真计算结果Fig.7 Simulation results of β control

转向角正弦输入，冰雪路面下车辆的运动状态响应如图8所示，有β控制时横摆角速度γ具有良好的跟踪效果，并且车体侧偏角β得到了有效的控制，车辆可以完成连续变道操作.无β控制时，车体侧偏角变得很大，车辆发生失稳，完全偏离预定车道，驾驶员无法对车辆进行有效控制来完成正常的变线操纵.

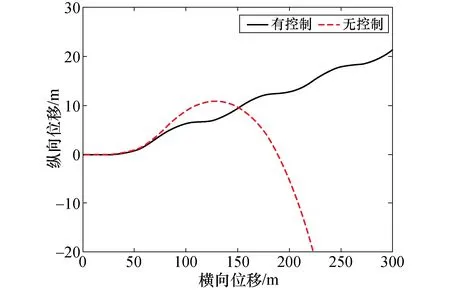
图8 车辆行驶轨迹的仿真计算结果Fig.8 Simulation results of vehicle trajectory

仿真得到的β和γ相平面轨迹如图9所示.在β控制下，车辆运动状态为有限的轨迹回路，并且始终保持在稳定区内.无β控制时，β和γ相平面轨迹呈发散状态，直到车辆状态偏离稳定区域.

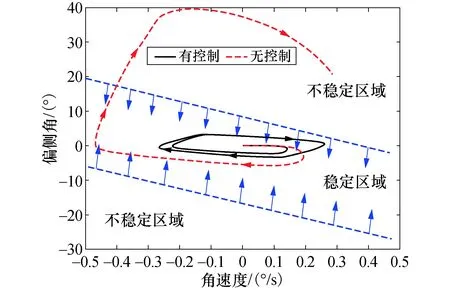
图9β-γ相平面轨迹的仿真结果Fig.9β-γphase plane trajectory of the simulation results

3 结论

1)提出了基于轮毂电机驱动电动汽车的车体侧偏角β观测与反馈控制方法，该方法利用轮毂电机驱动车辆的优点，可通过直接横摆力矩的控制保持车辆的稳定性.

2)在β观测器设计中，采用基于非线性轮胎模型的等效线性观测器及反馈系数的鲁棒控制算法.轮毂电机驱动电动汽车的实验结果验证了该观测器的有效性.

3)提出了基于模型跟踪和最优算法的直接横摆力矩决策控制方法,通过对β和γ的响应误差进行反馈控制补偿，计算出应施加的横摆力矩值，仿真结果表明该控制方法可有效提高车辆的稳定性.