连续体并联抓取机器人的结构设计及运动学分析

方跃法，林华杰

(北京交通大学 机械与电子控制工程学院，北京 100044)

抓取机器人作为工业生产线上最常见的机器人，是工件抓取、搬运、装配及码垛的主要工具[1].目前针对抓取机器人的研究和工业应用大多集中于串联机器人，而相较于串联机构具有更高精度、更大刚度等优点的并联机构，在抓取机器人的研究应用中也是以Delta系列机构为主的构型，其他构型较少应用于抓取操作[2].当然，并联机构也存在其自身的不足，如存在奇异性，工作空间小等因素限制了其应用和发展.近年来，一种模仿象鼻、蛇身躯干、章鱼触手的连续体机器人[3]，因其具有较大柔性、连续变形、灵活弯曲、工作空间大等优点被广泛研究，但其自身也存在精度不足、承载能力较弱的缺点.

连续体机器人，是一种具有弹性结构和无限自由度的，能够连续弯曲，不具有任何离散关节和刚性连杆的机器人[4].经典的连续体机器人如Clemson大学研制的仿象鼻连续体机器人[5]、仿章鱼触手的连续体机器人OctArm[6]等.仿蛇形、象鼻等生物结构的连续体机器人通常具有细长的结构，所以一直以来都被划分为串联机器人，但也有一部分利用多骨干并联形成细长结构的连续体机器人构型，如Ding等[7]提出的多脊柱蛇形机器人.因此，现有的大部分连续体机器人，可以被划分为串联或者混联机器人，而针对并联结构和连续体结构的结合构型研究仍然较少.

Zhu等[8]提出了一种用于纳米运动的柔性并联机器人，与具有挠性运动副的柔顺并联机构不同，该机构的连杆是用弹性材料做成，通过大的弯曲变形使动平台运动.德国Festo公司[9]研制的其第三代仿生三角运动装置通过4个弹性杆并联连接动平台与定平台，末端搭建仿鱼鳍的抓取装置，能实现自适应抓取操作任务. Bryson等[10-11]首次提出了并联连续体机器人(Parallel Continuum Manipulator)的概念，并设计了一种仿Stewart并联平台的新型并联连续体机器人.该机器人兼具有连续体机器人的轻量、灵活、紧凑和刚性并联机器人的稳定、刚度大等优点. Orekhov等[12-13]将并联连续体机器人的概念应用在医学领域，提出了适用于内窥镜手术的微型并联连续体机器人，构型上延续Bryson等提出的并联连续体机器人概念，在末端执行器上装有绳牵引的二自由度的夹持装置，可实现绳索远程驱动. 类似地，Altuzarra等[14]首次提出了Planar Continuum Parallel Robot的名称，并设计了一种二自由度的平面连续体并联机器人，该机器人由2个弹性杆连接1个末端运动点，在直线驱动器的驱动下弹性杆产生变形，从而推动末端运动点运动；虽然在名称上与Bryson等的提法具有差异，但其本质仍是综合了并联机构和连续体机器人特点的新型机器人.

为扩大并联机器人在抓取领域的应用，本文作者基于并联机器人结合连续体机器人的设计方法，提出一种新型的连续体并联抓取机器人.以弹性杆式的连续体结构代替刚性杆件和运动关节作为并联机器人的运动支链，末端抓取装置采用远程驱动，使机器人更具轻量化和柔顺性，具有较大的工作空间.首先对其进行了结构设计及三维建模.其次，运用等效D-H法建立了运动学模型，计算了正、逆解及雅克比矩阵.根据运动学方程，利用Matlab编程绘制出工作空间示意图.最后，将建立的三维模型导入Adams中进行虚拟样机的运动学仿真，对结构设计的合理可行性和运动性能进行了验证.

1 结构设计

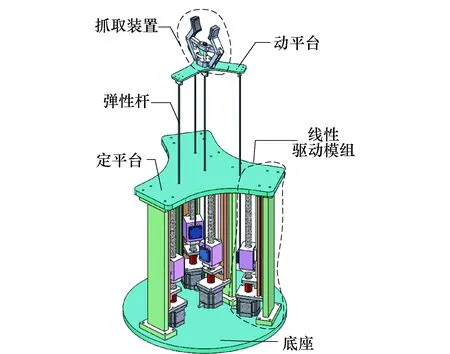
图1 连续体并联机器人机构图Fig.1 Structure of continuum parallel manipulator

传统的并联机构是由刚性连杆和运动副作为运动支链，多支链并联连接动平台和定平台，电机通过驱动副输入运动，并由支链传递至末端动平台，以一定自由度的运动形式输出.如图1所示，连续体并联抓取机器人由底座、定平台、动平台、弹性杆、直线模组和抓取装置组成.其中弹性杆代替传统的刚性连杆作为运动支链，3个外围弹性杆为动平台的驱动支链，中心弹性杆为抓取装置的驱动支链，所有运动支链上均无刚性运动副.弹性杆穿过定平台上的通孔，在通孔的位置约束下做轴向往复运动；其末端与动平台和抓取装置、起始端与驱动部件均采用固定连接，驱动的输入形式为线性运动.当3个驱动输入的位移相同且同步时，动平台做沿竖直方向移动运动；当输入位移不同或者不同步时，弹性杆会发生弯曲变形，从而使动平台作空间转动运动. 驱动电机均置于定平台下方，使动平台更具轻量化.

弹性杆采用直径为2 mm的镍钛合金丝，长度为200 mm，外围弹性杆至中心弹性杆的距离为60 mm.驱动部分采用行程为200 mm的线性模组，见图2，其整体长度为400 mm.该线性模组能够将电机的转动输入转化为直线移动输出，以驱动弹性杆在竖直方向移动.利用电机驱动丝杠转动，丝杠上配置螺母，并装有弹性杆紧固件以固定弹性杆一端，螺母连接件与直线滑块固定连接，在导轨上移动.

图 2 线性驱动模组示意图Fig.2 Linear actuation module

抓取装置采用对称的连杆机构形式，如图3所示，连杆末端装有橡胶垫，通过中心弹性杆的移动驱动带动对称连杆定轴转动，连杆的开闭运动可以实现对目标对象的抓取和放开操作. 中心弹性杆在动平台运动阶段不断调整以使连杆抓取机构的驱动杆与动平台保持相对静止，动平台运动位姿确定后，外围弹性杆保持状态，而中心弹性杆继续调整以驱动抓取装置实现开闭运动，对物体进行抓取操作.

图3 抓取装置示意图Fig.3 Grasping mechanism

2 运动学及性能分析

2.1 运动学建模概述

根据连杆式弹性杆驱动连续体并联机构的运动形式，忽略末端抓取装置，只保留运动构件，将机构化简作运动简图，如图4所示.其中，杆0为中心弹性杆，杆1、杆2、杆3为外围弹性杆.假设弹性杆在变形时是等曲率连续弯曲变形[15]，且连杆的材料特性使其弯曲时纵向长度不发生变化.

图4 连续体并联机器人运动简图Fig.4 Kinematic diagram of continuum parallel manipulator

初始状态下，弹性杆为无变形的竖直状态，外围弹性杆在动平台和定平台上的连接点形成两个相同的等边三角形几何关系.在定平台等边三角形的重心点建立基础坐标系O-XYZ，其中Z轴垂直于定平台所在平面，正方向指向动平台，X轴的正方向指向杆2，利用右手法则确定Y轴的正方向，O点到三角形顶点的距离为s0.将基础坐标系O-XYZ沿Z轴平移到动平台的等边三角形重心点，建立移动坐标系O1-X1Y1Z1，其中Z1轴始终垂直动平台所在的平面，并指向外侧，X1、Y1轴方向的确定方式同基础坐标系.

弹性杆在动平台和定平台之间的长度为其杆长，用li表示，杆长变化量用Δli表示，初始状态下的杆长由结构尺寸决定，用lk表示.

弯曲状态下，中心弹性杆弯曲圆弧所在的平面为弯曲平面，O1-X1Y1平面与O-XY平面的夹角为弯曲角β，弯曲平面与O-XZ平面的夹角为旋转角α.中心弹性杆弯曲圆弧对应的半径为r，圆心点为Ob，则弧长与半径的关系为

(1)

动平台中心点O1的位置为P(x,y,z)，其在基础坐标系下的表达式为

(2)

由于在连续体并联抓取机器人中，无关节变量的概念，其动平台的位置和姿态变化是通过调节3个外围弹性杆长度变化量实现的，因此引入虚拟关节变量和虚拟关节空间[16]对其运动学进行描述，见图5.

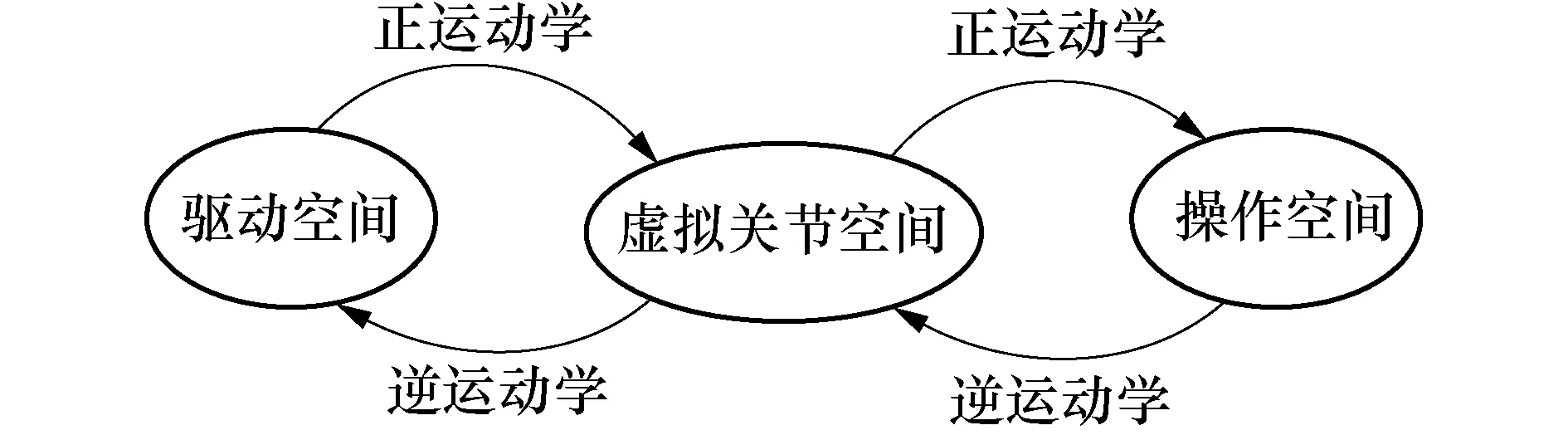
图5 连续体并联机器人的运动学空间关系Fig.5 Kinematic space relation of continuum parallel manipulator

图中,旋转角α和弯曲角β为虚拟关节变量，形成虚拟关节空间；驱动量为弹性杆的杆长变化量Δli，形成驱动空间；末端动平台的位置P(x,y,z)和姿态o(θ,φ,γ)形成操作空间，也称为任务空间.3个空间的变量之间形成互相映射的关系，对驱动空间-虚拟关节空间-操作空间的计算为连续体并联抓取机器人的运动学正解分析，反之为运动学逆解分析.

2.2 虚拟关节空间-操作空间的映射

在传统的刚性机器人运动学分析中，以关节变量为参数求解机器人末端执行器的位置和姿态问题，通常采用D-H法.在对连续体并联抓取机器人进行运动学建模时，由于不存在刚性关节，无法直接用D-H法对连续体支链的运动状态进行参数化描述，因此采用等效D-H法进行运动学建模和分析.

在等曲率连续弯曲变形的假设下，求解末端动平台的位姿问题，可以转化为定平台上的基础坐标系O-XYZ和动平台上的移动坐标系O1-X1Y1Z1

之间的齐次变换矩阵问题，变换顺序如下：

1)将中心点O平移至末端动平台中心O1，则其平移矩阵为

(3)

2)将坐标系绕Z轴旋转α角，其旋转矩阵为

(4)

3)将坐标系绕新的Y轴旋转β角，其旋转矩阵为

(5)

4)将坐标系绕新的Z轴旋转-α角，其旋转矩阵为

(6)

联立式(3)～(6)的变换矩阵，可得基础坐标系O-XYZ到移动坐标系O1-X1Y1Z1的齐次变换矩阵T为

(7)

式中：sα、sβ和cα、cβ分别为sinα、sinβ和cosα、cosβ.

2.3 操作空间-虚拟关节空间的映射

若末端动平台的位姿已知，其在基础坐标系O-XYZ中的位姿矩阵A由矢量n、o、a、p表示为

(8)

齐次变换矩阵T和位姿矩阵A均表示末端动平台在基础坐标系中的位姿，故矩阵T、A中的对应元素彼此相等，可得

(9)

根据具体已知条件中的az、px、py的值便可以求解出对应的末端动平台位姿下的虚拟关节变量α和β.

(10)

2.4 虚拟关节空间-驱动空间的映射

作O-XY所在平面的俯视投影示意图和弯曲平面剖面示意图，如图6所示.

图6 局部投影示意图Fig.6 Partial projection

在弯曲平面上l1、l2、l3所在圆弧分别对应的半径为r1、r2、r3，根据几何关系可得

(11)

根据弧长与半径的几何关系可解得出末端动平台的虚拟关节变量和各弹性杆的驱动量之间的关系

(12)

2.5 驱动空间-虚拟关节空间的映射

驱动空间至虚拟关节空间的映射关系为驱动量Δli与虚拟关节变量α和β之间的对应关系.联立式(12)中的Δl1等式和Δl2等式，可得

(13)

联立式(12)中的Δl1等式和Δl3等式，可得

(14)

联立式(12)中的Δl2等式和Δl3等式，可得

(15)

2.6 雅克比矩阵分析

连续体并联抓取机器人的微分运动学描述的是弹性的杆输入驱动量和末端动平台的运动线速度、角速度之间的映射关系.根据式(8)，正运动学方程可以化为如下形式

(16)

末端动平台中心的位置坐标P(x,y,z)可以表示为

(17)

末端动平台的姿态空间欧拉角o(θ,φ,γ)可以表示为

(18)

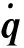
(19)

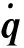
(20)

(21)

联立式(18)(19)，化简可得

(22)

式中：J为6×3矩阵，是机器人的运动学雅克比矩阵.

式(20)为连续体并联机器人的微分运动学方程，表征了末端动平台的运动速度和弹性杆驱动速度之间的关系.

2.7 工作空间分析

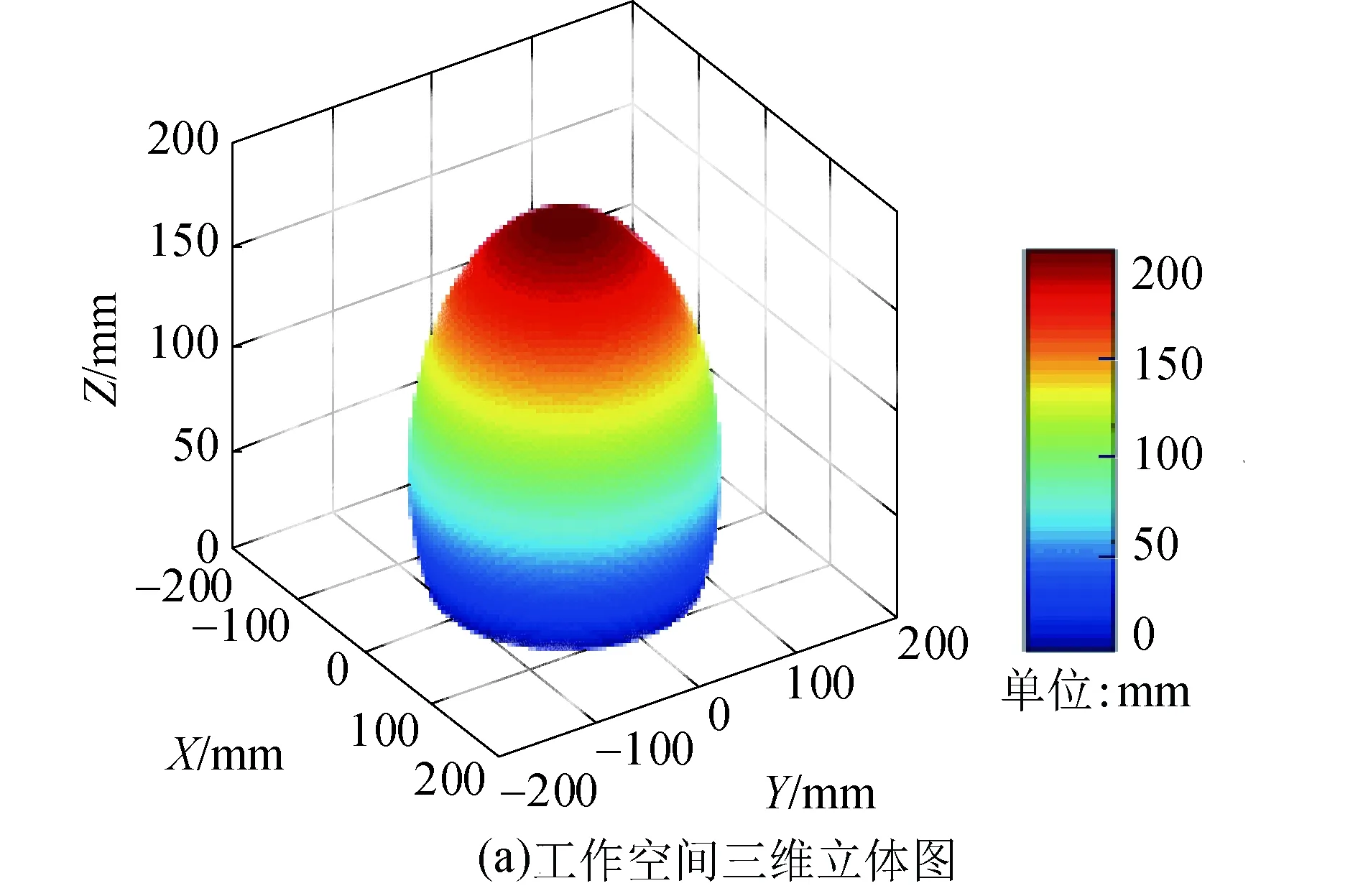
根据正运动学的表达式(7)以及虚拟关节变量α和β的变化范围可以确定末端动平台中心点的可达工作空间范围，中心弹性杆的杆长l0的变化范围为80～180 mm.基于蒙特卡洛方法[17]编写Matlab程序，绘制末端动平台末端中心点的可达工作空间如图7和图8所示.

分析工作空间立体图和局部图可知，连续体并联抓取机器人具有比自身结构尺寸还大的可达工作空间范围，由于其末端可达位置受驱动器的行程范围影响，最低运动范围受限，故在工作空间中为一个中空的球状包络区域.因此在面向具体任务时应注意结构尺寸和驱动行程的设计，使可达工作空间满足设计任务要求.

3 运动学仿真模拟

为了验证结构设计的准确性和可行性，基于Adams软件对连续体并联抓取机器人进行虚拟样机的运动学仿真.在Solidworks中将样机三维模型进行数据交换接口转换到Adams/View中，对导入的构件赋予材料属性，并在构件间定义运动副，并对构件施加载荷，对驱动副添加驱动，赋予驱动函数，设定时间和步长对样机进行运动仿真模拟.由于虚拟样机中的弹性杆在初始三维建模时是以刚性构件建立的，需要在Adams/View模块中将其转换为柔性体.

在基础设置完毕后，输入驱动函数如下：

Δl0= STEP (time, 0, 0, 5, 100) + STEP (time, 5, 0, 10, -100) + STEP (time, 10, 0, 15, 25) + STEP (time, 15, 0, 20, -25)；

Δl1= STEP (time, 0, 0, 5, 100) + STEP (time, 5, 0, 10, -100) + STEP (time, 10, 0, 15, 50)；

Δl2= STEP (time, 0, 0, 5, 100) + STEP (time, 5, 0, 10, -100) + STEP (time, 10, 0, 15, 50)；

Δl3= STEP (time, 0, 0, 5, 100) + STEP (time, 5, 0, 10, -100) + STEP (time, 10, 0, 15, -50).

设定仿真时间为20 s，进行运动学仿真模拟，仿真及运动过程图9所示.

图9 仿真运动过程示意图Fig.9 Diagram of motion process simulation

由运动过程可知，连续体并联机器人样机能够在虚拟样机仿真界面实现沿Z轴方向的平移运动和全周范围的弯曲转动，具有三自由度，能够实现大范围空间抓取搬运操作，说明了虚拟样机三维结构设计的合理性和可行性.仿真完毕后，可导出动平台中心在X、Y、Z轴方向的位移运动曲线和驱动弹性杆的输入位移曲线如图10所示.

图10Adams运动学仿真曲线Fig.10 Simulation curves Adams kinematics

由图10可知，在0～10 s时，图9(a)和图9(b)相应的曲线变化趋势相同，说明当弹性杆的运动方向和位移一致时，动平台沿Z轴平移的距离与输入的行程一致；在10～15 s时，弹性杆2和弹性杆3的位移方向不一致，动平台在弹性杆的弯曲变形下发生转动，动平台的X、Y、Z位置发生变化；在15～20 s时，动平台位置基本保持不动，此时杆0做负的位移运动，使抓取装置闭合从而进行抓取操作.运动曲线较为平滑无突变，说明运动平稳可行，进一步证明了连续体并联抓取机器人设计的正确性.

4 结论

1)设计了一种新型的连续体并联抓取机器人，利用弹性杆作为连续体运动支链代替传统并联机器人的刚性运动支链，末端抓取装置采用远程驱动，实现了柔顺化和轻量化.

2)对连续体并联抓取机器人进行了运动学建模，计算出正、逆解和雅克比矩阵，绘制了运动空间，证明其具有大的工作空间.

3)利用Adams将三维模型进行运动学仿真，得到了运动过程示意图和运动学曲线，仿真结果表明机器人具有3个自由度，运动性能和抓取性能良好，结构设计合理可行，为后续研究奠定了理论基础.