中考情景应用题的归类及教学探讨

杨国华

摘 要：中考备考复习教学的有效性关乎众多学子的学业生涯命运。如何科学、合理地设计教学内容，且精心地组织课堂教学是毕业班教学需要研究的问题。文章基于初中数学中考情景应用题角度，认为教师需要认识备课复习的重要性，在分析新情景应用题专题研究的实际意义基础上选择众多试题资料进行有效归类与分析，探讨新情景应用题的解决策略。

关键词：初中数学;备考复习;情景应用题;归类

中图分类号：G633.6 文献标识码：A 收稿日期：2019-02-24 文章編号：1674-120X（2019）22-0038-02

新情景应用题因源于生活实际，需要考生大量的生活实际经验或体验。然而面对学生中学阶段的学业繁重的现实局面，教师往往心有余而力不足。教师的备考复习教学，需要多渠道搜集新情景题型，并对其进行有效归类，让学生能知晓新情景应用题的几大类考试方向或者命题思路。文章基于教学实际经验，先论述新情景应用题的特点及其实际意义，进而探讨试题的类型及有效的解题应对策略。

一、新情景应用题教学研究的实际意义探讨

新情景应用题是理论联系实际，以“学以致用”为宗旨的一种试题，在近几年全国各地的中考中频频出现，成为中考的热点。它充分体现了数学的价值和教育改革的方向。新情景试题选题材料新颖，符合时代社会发展需求，如2017年福建中考的共享单车使用问题与2018年福建中考快递员揽件寄件材料，这些都给考生一种身临其境的体验。共享单车与快递业务发展是近几年中国发展的民生大事，对考生而言，或多或少都有了解。新情景应用题呈现在中考试题中，旨在考查学生语言文字理解能力，考查考生的数学语言转换能力，更考查学生的数学建模能力及其应用数学的意识。为此，教师需要从多角度、多渠道搜集这类试题，让学生接触这些源于生活实际的新情景应用题。对教师而言，教学的难点在于能否将实际问题转化为数学问题，在思考实际问题中从数学思维、数学建模等角度去审题，做到实事求是地解决问题，提升学生的解题能力。

二、新情景应用题题型归类及解答策略

无论是代数型试题还是几何型试题，都考查学生的数学基本功：理解题目中的数学逻辑关系，理清题目文字与图形意思，巧妙利用数形结合、建模思想等方法，有效解答步骤规范性等。文章结合以下几种题型进行有效探讨：

题型一：方程型新情景应用题

方程（组）是初中数学重要知识内容，涉及一元一次方程、二元一次方程组等知识，在中考新情景应用题中自然少不了考查这方面的知识。

例1：国家“家电下乡”政策实施中，我国农民购买家电类产品，政府会以原价购买总额的13%给予补贴，并返还给购买者。幸福村众多农民到某商场购买同一型号的冰箱、电视机，已知他们购买冰箱数量是电视机的2倍，且按原价购买冰箱总额为4000元、电视机总额为15000元。结合国家“家电下乡”的优惠政策，每台冰箱补贴返还的金额比每台电视机补贴返还的金额多65元，请问幸福村农民冰箱、电视机各购买多少台？

（1）设购买电视机x台，依题意填充下列表格：

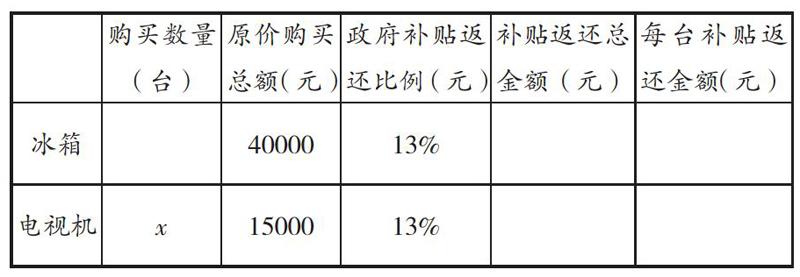
（2）列出方程（组）并解答。

基于这道试题的背景材料是“家电下乡”的国家政策，具有时代发展特点，对很多学生而言不会陌生。在了解题目中材料后，教师引导学生理清题目关系，分清方程或方程组类型。为此，在审题中需要理清如下关系：每台家电的返还金额=原价每台的购买金额×13%，补贴返还总额=每台的返还额×购买数量;由题目材料分析的等量关系已知关键语“每台冰箱补贴返还的金额比每台电视机补贴返还的金额多65元”就可得出方程。解此类应用题重点在于准确地找出相等关系，这是列方程的依据，也要注意题目中给出的条件。

题型二：函数型新情景应用题

函数也是初中数学的重要内容，能为实际生活解决诸多问题。新情景应用题涉及函数相关模型需要建立符合的函数模型。建立函数模型，通过研究函数的性质，解决日常生活中可能遇到的实际问题，为生产生活进行决策，实现真正意义上的学以致用。

例2：美好生活材料店为A公司代理一种建筑材料（题目中的代理是指公司免费提供货源，待货物售出后，再进行结算，未售出的由公司负责处理）。当每吨售价为260元时，月销售量为45吨。若美好生活材料店为提高营业利润，适当采用降价方式进行销售。门店业务员经过一段时间降价促销调查发现：当每吨材料售价每下降10元时，月销售量就会增加7.5吨。鉴于经销各方面原因，门店每售出一吨建筑材料需支付公司及其他费用100元。现在假设每吨材料售价为x（元），该材料店的月利润为y（元）。

现在根据以上题目设计如下需要解决的问题：①材料店将每吨定价为240元时，请计算当月售量;②试求出x与y的函数关系式（无须写出x的取值范围）;③若材料店要想取得最大月利润，售价应是每吨多少元？④材料店业务员小兰说：“当月利润最大时，月销售额也最大。”你觉得对吗？请说明理由。

题型三：几何型新题型应用题

几何型新题型应用题也是中考常考题目，教师需要引导学生多关注题目与涉及图形的关系，利用数形结合思想解决问题。为此，学生需要夯实几何图形数学基础知识，在实际题目中将几何模型描述出来，从而有效完成这类几何实际应用问题。

例3：图甲是我们家庭中常见的水桶，其水桶提手结构的平面图是轴对称图形。设⊙O为桶口所在圆，OA为半径，当点O到线段BC（或线段DE）的距离大于或等于圆的半径时，提手会从图甲的位置转到图乙的位置，这样的提手才合格。现工人师傅用钢筋做了一个水桶提手（如图丙A—B—C—D—E—F，其中C—D为圆弧，其他都是线段），O是AF的中点，桶口直径AF=34cm，AB=FE=5cm，∠ABC=∠FED=149°。请根据你学过的知识判断工人师傅做的水桶提手是否合格。

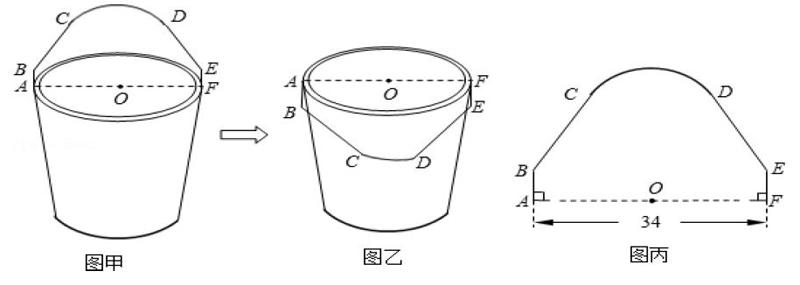
这道试题源于学生熟悉的家庭厨房生活用途中的水桶，题目中对水桶提手进行分析，涉及圆、圆弧、轴对称、三角形知识。本题主要考查了解直角三角形，根据AB=5，AO=17，得出∠ABO=73.6°是解决问题的关键。在备考复习中，这类几何图形试题需要在复杂的图中找出几何关系，运用几何相关性质、定理等进行分析，从而求解题目。

题型四：统计概率型新情景题

对于统计概率方面的新情景应用题，这类试题文字材料很多，在审题时需要认真，甚至在题目中有一些图表之类需要填写。

例4：2018年福建中考试题：甲乙两家快递公司揽件员的日工资方案如下：甲公司为“基本工资+揽件提成”，其中基本工资为70元/日，每揽收一件提成为2元;乙公司无基本工资，仅以揽件提成计算工资，若当日揽件数不超过40，每件提成4元;若当日揽件数超过40，超过部分每件多2元提成。下图是今年四月份甲公司揽件员人均揽件数和乙公司揽件员人均揽件数的条形统计图：

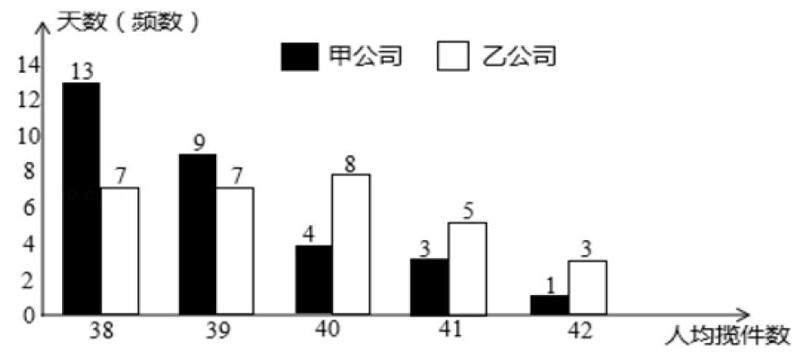
（1）现从今年四月份的30天中随机抽取1天，求这一天甲公同揽件员人均揽件数超过40（不含40）的概率;

（2）根据以上信息，以今年四月份的数据为依据，并将各公司揽件员的人均揽件数视为该公司各揽件员的揽件数，解决以下问题：①估计甲公司各揽件员的日平均揽件数;②小明拟到甲、乙两家公司中的一家应聘揽件员，如果仅从工资收入的角度考虑，请利用所学的统计知识帮他选择，并说明理由。

针对这道试题，学生需要认真分析题目，文字材料很多，不能因为文字太多马虎阅读。在统计概率类题目中，很多学生觉得数据很枯燥。教师需要引导学生用科学的眼光去观察数据、处理数据，让数据帮助我们解决实际问题。

综上所述，如何将新情景应用题等专题复习设计得有效、合理、科学，符合学生认知规律，需要教师不断去研究。“千里之行，始于足下。”要想真正优化中考备考复习数学课堂教学，需要一步一个脚印地付诸行动。

参考文献：

[1]彭聪聪.中考数学“数与式”应用性试题的类型及解题思路[J].数理化學习（初中版），2014（6）：50-51.

[2]易良斌，赵满宏.回归课本 融通方法 关注生活——新课程背景下的中考数学复习思考[J].教学月刊（中学版），2007（1）：54-56.