Limit Cycles by Perturbing a Piecewise Near-Hamiltonian System with 4 Switching Lines

WANG Hao(王皓),LIANG Feng(梁峰)

(School of Mathematics and Statistics,Anhui Normal University,Wuhu 241000,China)

Abstract: By using the first order Melnikov function method for piecewise near-Hamiltonian systems,we study limit cycle bifurcations by perturbing a compound global center with 4 regions.When the perturbed terms are polynomials with degree n, we give the number of limit cycles bifurcated from the center.

Key words: Piecewise smooth dynamical system;Limit cycle;Bifurcation;Melnikov function

1.Introduction And Main Results

For many applications involving biology,medicine,friction and devices with switching components,piecewise smooth (PWS) dynamical systems are more precise to model these problems.As a consequence,the study of PWS systems has become very active in the last decades.One of the most important problems about PWS dynamical systems is how to determine the number of limit cycles.The problem is much more difficult than that in smooth systems.So far,there have been at least three common ways to consider multiple limit cycles for a given PWS system.The first method is to study small amplitude limit cycles that bifurcate from Hopf or center bifurcation[1−2,7,9].The second is to study limit cycles which bifurcate from a periodic annulus[3−5].The third method is to study the multiple limit cycles through homoclinic bifurcation[8,13,16].

Most of works assumed that discontinuity sets of PWS planar systems consist of only one switching manifold,particular a straight line.[7−10,13,17]However,as pointed out by Akhmet and Arugaslan[6],due to exterior effects,discontinuities may occur on multiple lines,curves or surfaces.Recently,some work has been done on PWS dynamical systems with multiple switching lines.[12,14−15]In [12],HU and DU studied bifurcations of periodic orbits in discontinuous planar systems,whose discontinuities occur on finitely many rays starting at the origin.More precisely,they considered the following system

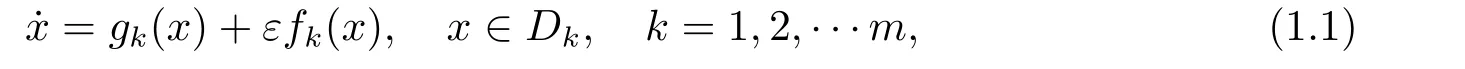
whereDkis the open region between the switching rayslkandlk+1fork=1,2,···m,andlm+1=l1,gk,fk∈C2(Dk ∪lk ∪lk+1,R2),|ε|≤ε0for someε0>0.Forε=0,the unperturbed system is given by

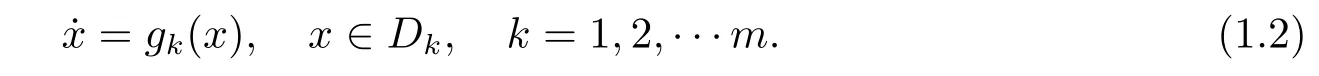
By establishing the first order Melnikov function for system(1.1),the authors considered limit cycle bifurcations for several piecewise systems with low degree perturbations.

Further,in[11]WANG and HAN considered the piecewise near-Hamiltonian system with 4 regions

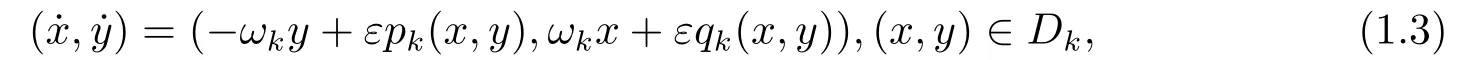
k=1,2,3,4.Here,D1,D2,D3,D4denote the first,second,third and fourth quadrants,respectively.The unperturbed systems of(1.3)has a global center at the origin.They proved that systems (1.3) havenlimit cycles around the origin undernth-degree perturbations.

In this paper,we study limit cycle bifurcations for a class of perturbed planar discontinuous system with 4 switching rays as follows

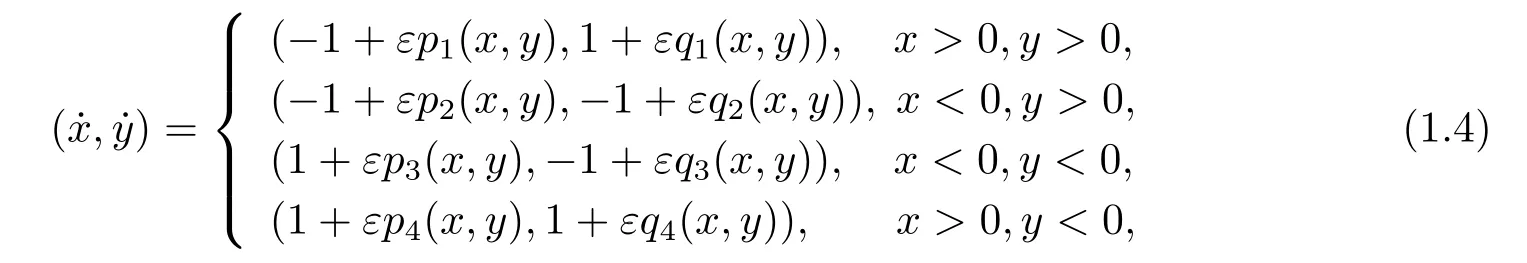
where

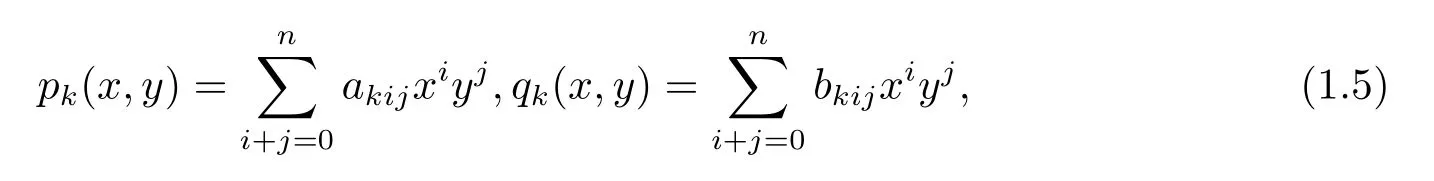
fork=1,2,3,4.

It is obvious that the unperturbed system of (1.4) is different from that of system (1.3),although it also has a global center at the origin.For system (1.4),we have the main result below.

Theorem 1.1Let (1.5) hold.Then forε >0 small system (1.4) has at mostnlimit cycles on the plane if the first order Melnikov function of system (1.4) does not vanish identically.Moreover,the upper bound can be achieved.

2.Fundamental Lemmas and the Proof of the Main Result

First,we assume that the space R2is splited into 4 disjoint regions by four raysΣ1,Σ2,Σ3,Σ4,and letΣ5=Σ1,where

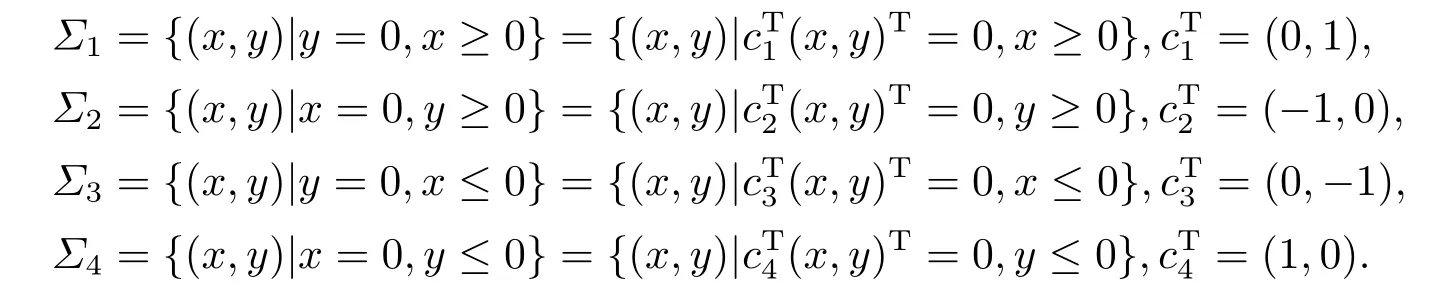
The open region betweenΣkandΣk+1was denoted byDkfork=1,2,3,4.Then,

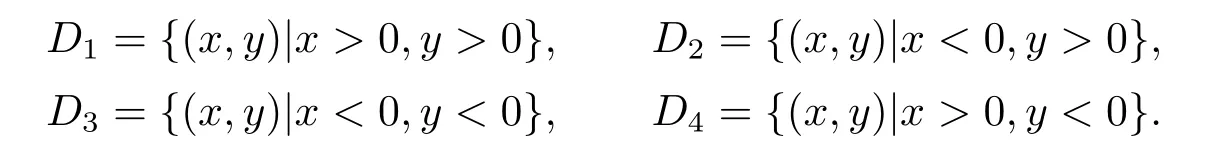
It is easy to see thatDk ∩(Σk ∪Σk+1) is empty fork=1,2,3,4.

In order to give the first order Melnikov function of system(1.4),we consider the following planar piecewise system defined onD1∪D2∪D3∪D4

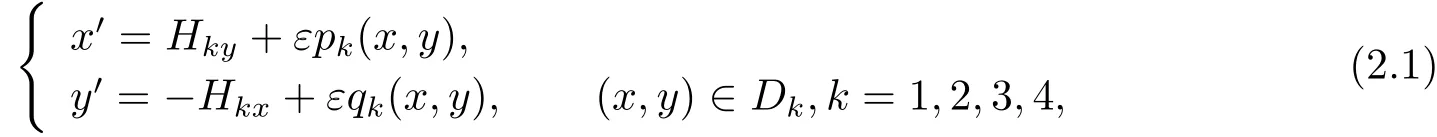
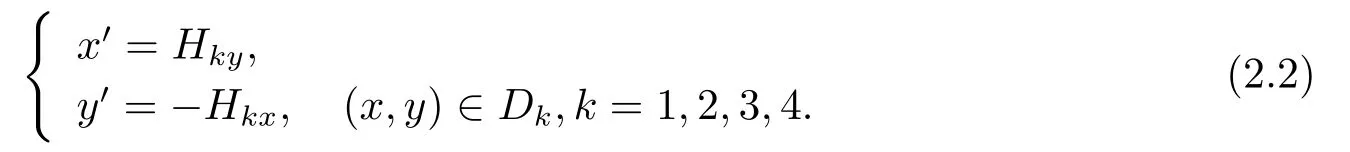
For the system (2.2),we give the following two hypotheses first.

(H1) There exist four pointsA1=(a1(h),0),A2=(0,a2(h)),A3=(a3(h),0),A4=(0,a4(h)),Ak∈Σkfork=1,2,3,4,and an intervalJ=(0,α)such that forh∈J,H1(A1)=H1(A2)=h,H2(A2)=H2(A3),H3(A3)=H3(A4),H4(A4)=H4(A1),wherea1(h)>0>a3(h),a2(h)>0>a4(h).

(H2) System (2.2) has a family of periodic orbitsLh=L1h ∪L2h ∪L3h ∪L4h,h∈J,surrounding the origin counterclockwise.Fork=1,2,3,4,letAkbe the intersection ofLhwithΣk,andLkhbe the intersection ofLhwithDk.We have

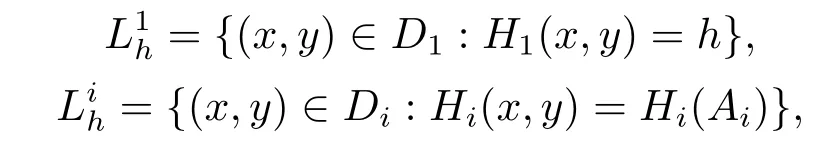
wherei=2,3,4.

By (H1) and (H2),we can see that the orbit of system (2.1) starting fromA1atΣ1crossesΣ2,Σ3,Σ4,Σ1in turn.For|ε|small,letAiεdenote its first intersection point withΣi,i=2,3,4,and letBεdenote the second intersection point withΣ1when it returns toΣ1for the first time.And setA2ε=(0,a2ε(h)),A3ε=(a3ε(h),0),A4ε=(0,a4ε(h)),Bε=(a1ε(h),0).Similar to Theorem 2.2 in [12]we have

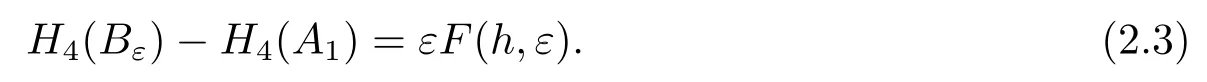
It is clear that the functionFin (2.3) is smooth becauseAiε,i=2,3,4 andBεare smooth in(ε,h).The functionF(h,ε)is called a bifurcation function of system(2.1).So the system(2.1)has a periodic orbit nearLh0forh0∈Jif and only ifBε=A1for(h,ε)near(h0,0).It follows that an isolated zero ofFinhcorresponds to a limit cycle of (2.1).LetM(h)=F(h,0).ThenM(h) is called the first order Melnikov function of the system (2.1).

From [11],we have the following lemma for the expression ofM(h).

Lemma 2.1Suppose that (H1) and (H2) hold.Then the first order Melnikov functionM(h) of system(2.1) has the following form

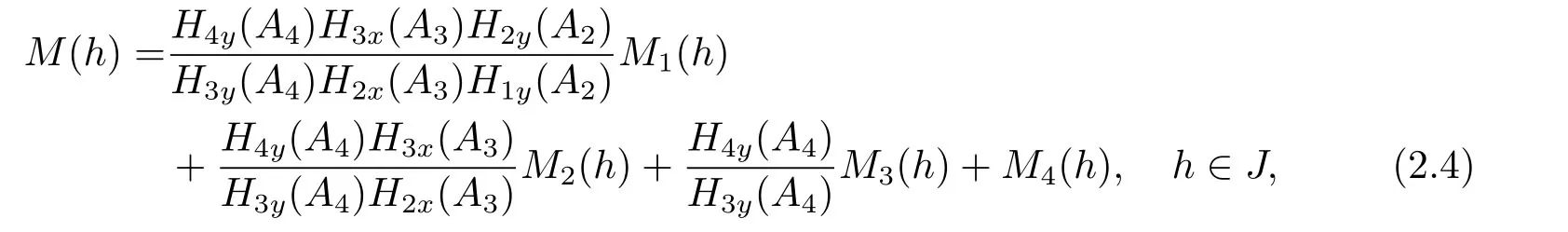
For system (1.4),it is clear that

H1(x,y)=−y−x=h,H2(x,y)=−y+x,H3(x,y)=y+x,H4(x,y)=y−x.

By Lemma 2.1,for system (1.4) we have

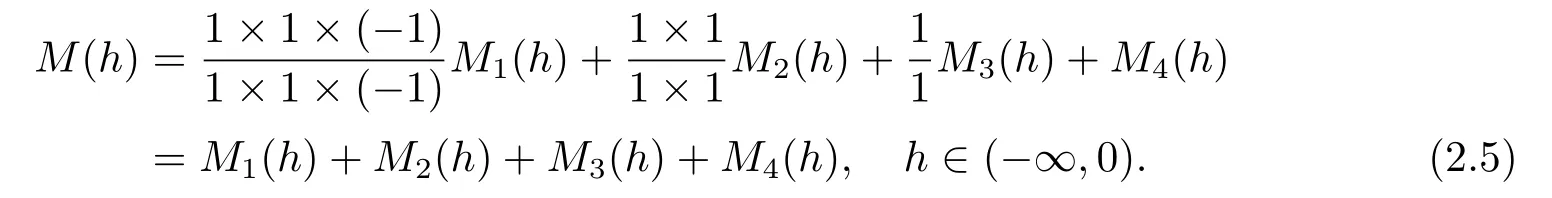
Lemma 2.2Suppose(1.5)holds,the functionM1(h)in(2.5)has the following expansion

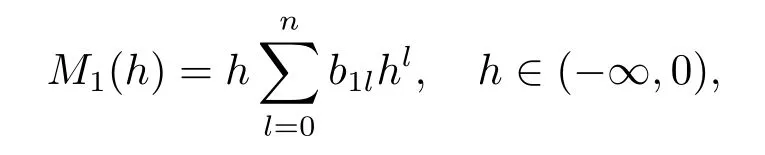
ProofBy Lemma 2.1 and (1.5),we get forh∈(−∞,0)

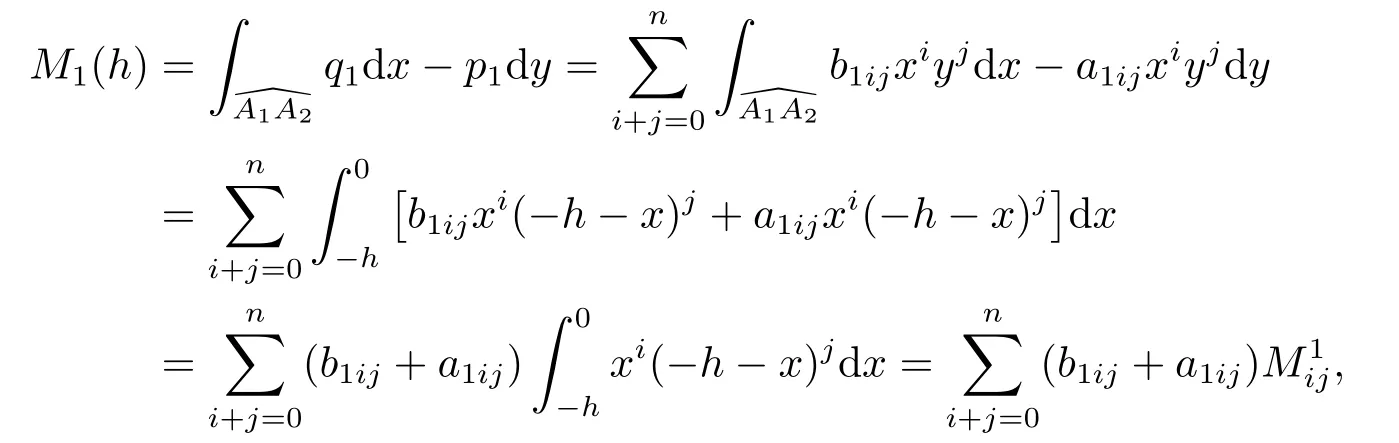
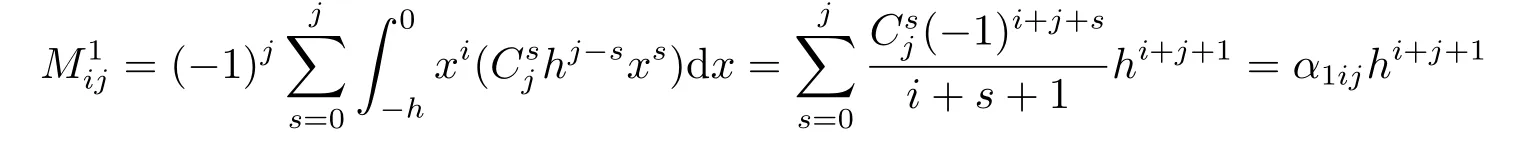
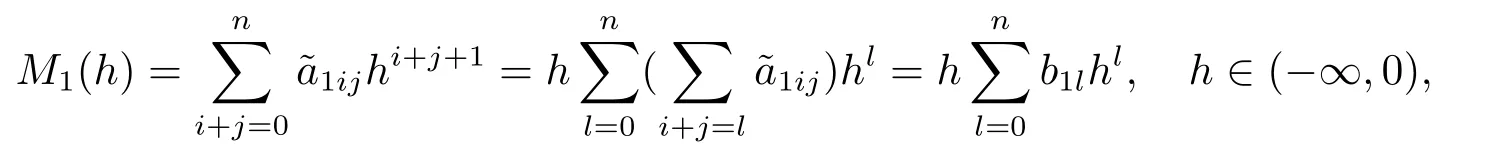
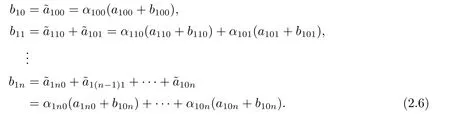
Let

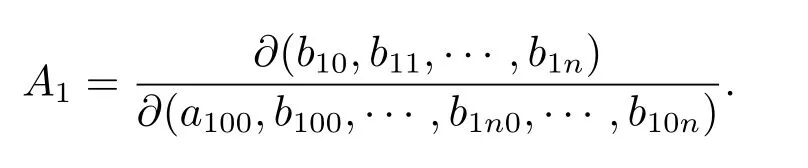
By (2.6),we have

Note thatα1i0=We see that Rank(A1)=n+1,which means thatb10,b11,b12···b1ncan be taken as free parameters.The proof is completed.

Remark 2.1We can use the similar method as Lemma 2.2 to get

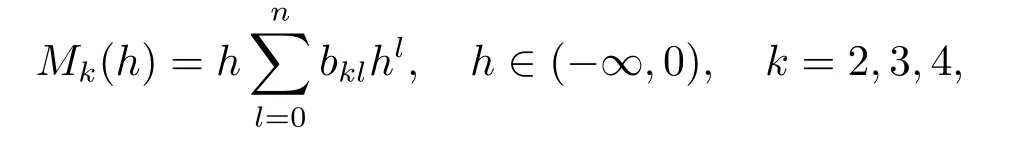
where

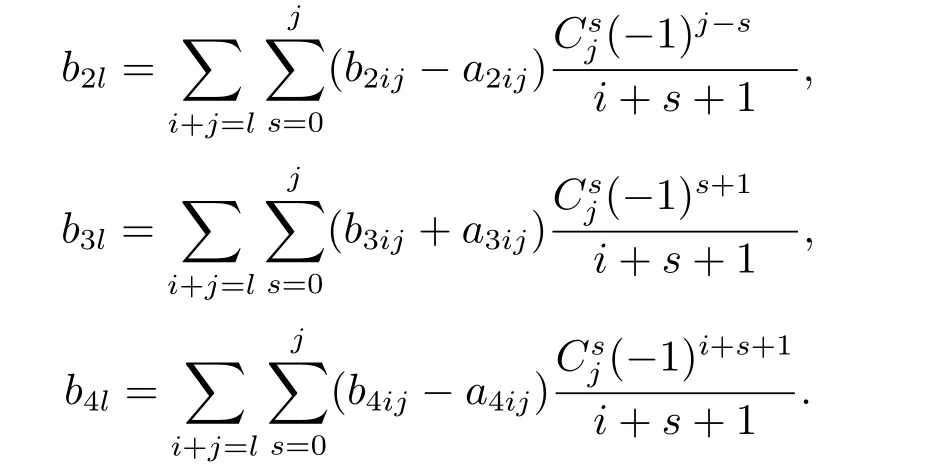
Moreover,for eachk∈{2,3,4},bk0,bk1,bk2···bkncan be also taken as free parameters.

By Lemma 2.2 and Remark 2.1,it is easy to obtain the lemma below.

Lemma 2.3Let (1.5) hold.Then,for the system (1.4) we have

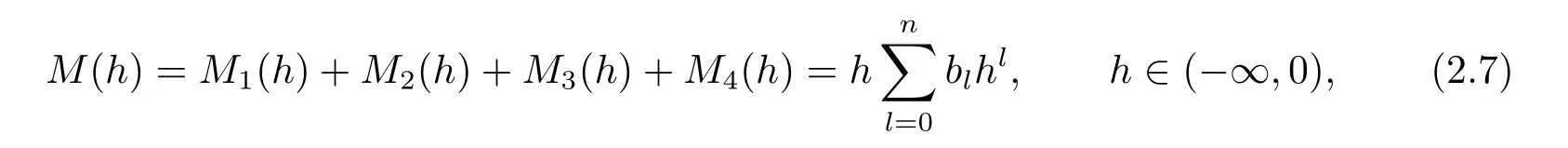
wherebl=b1l+b2l+b3l+b4l.Obviously,b0,b1,···,bncan be taken as free parameters.

Proof of Theorem 1.1By Lemma 2.3,we know

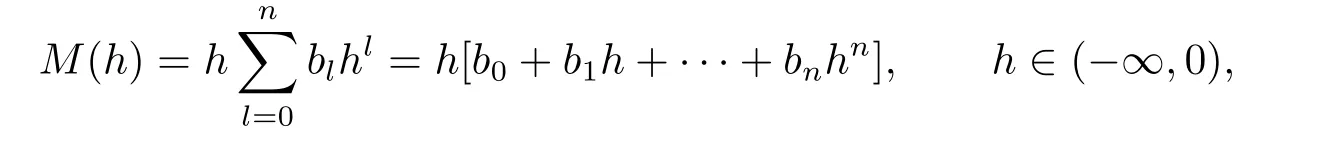
whereb0,b1,···,bncan be taken as free parameters.It is clear thatM(h)has at mostnzeros in the interval (−∞,0) ifM(h)0.This means that forε>0 small the system (1.4) has at mostnlimit cycles on the plane.On the other hand,we show thatnnegative simple zeros ofM(h) can appear nearh=0.Sinceb0,b1,···,bncan be taken as free parameters,we first takeb0=b1=···=bn−1=0 and (−1)nbn >0 such thatM(h)>0 forh<0.Then,we only changebn−1withbnbn−1>0 and|bn−1|≪|bn|.This meansM(h)=bn−1hn−1(1+O(h))<0 for−h>0 small.Hence,M(h) has a negative simple zero nearh=0,denoted byh1.Using the same method,we changebn−2,bn−3,···,b0in turn such that

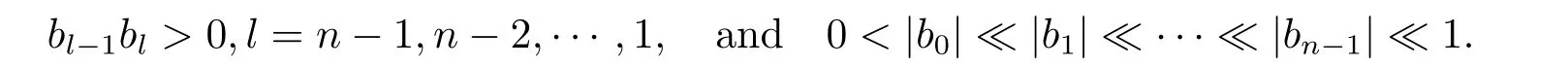
Then,othern−1 negative simple zerosh2,h3,···,hnare found with 0<|hn| ≪|hn−1| ≪··· ≪|h1|.Therefore,nlimit cycles can appear near the origin for system (1.4).This completes the proof.