初等交换群凯莱图的完备码与完全图的正则覆盖

张 星,王 燕

(烟台大学数学与信息科学学院,山东 烟台 264005)

1 引言与预备知识

自20世纪40年代后期出现编码理论以来,完备码成为了信息论中研究的一个重要课题[1-2].众所周知,Hamming和Golay码是两类重要的完备码.在经典完备码问题中长度为n的q-元完备e-码恰好是Hamming图H(n,q)中的完备e-码[3-4],因此完备码的概念可以以一种自然的方式延伸到图中.而Hamming图是一类特殊的凯莱图,因此凯莱图中的完备码问题可以看作经典完备码问题的一种泛化[2].由于凯莱图中的完备码与编码理论、群论和图论有着密切的关系,因此近几年来凯莱图中的完备码问题得到了相当的重视并被广泛研究.

令Γ为一连通的无向简单图,记Γ的顶点集合为V(Γ),边集合为E(Γ),对任意点v∈Γ,记N(v)为与v相邻的点的集合.假定S⊂V(Γ)是一个非空子集,若对任意的v∈V(Γ),存在唯一的s∈S使得d(v,s)≤1(d(v,s)表示两个点之间的距离),则称S为图Γ的完备码.由完备码定义可知S是一个独立集,而且S之外的顶点,有且只有一个S中的顶点与它相邻.在图论中完备码也被称作有效控制集或独立的完备控制集.

设G是一个有限群,X={x1,x2,…，xn}是G的一个子集,如果X满足X-1={x-1:x∈X}=X且1G∉X,则称X是G的一个Cayley子集.凯莱图Cay(G,X)中的顶点集为群G中的元素,任意两点g、h∈G之间有连边当且仅当存在点xi∈X,使得h=gxi成立.Cay(G,X)是连通的当且仅当G=〈X〉.Cayley图中与某点相连的边的数目称为该点的度数.

凯莱图中的完备码问题得到了广泛讨论.例如,TERADA[5]证明了对共轭封闭的连通集,SL(2,2f)(f>1)任意的凯莱图中都不存在完备码.Gaussian和Eisenstein-Jacobi图中存在完备t-码的充分条件在文献[6]中给出,后来这些条件又被证明在更一般的情况下是必要的[7].ETIENNE[8]利用基础群的不可约特征证明了有共轭封闭的连通集的凯莱图中存在完备码的必要条件.DEJTER和SERRA[9]于2003年提出了在对称群的凯莱图上构造有限e-链寻找完备码的方法.HUANG等[10]从群环的角度研究了凯莱图中的完备码,其中给出了有限群的正规子群可作为完备码的条件.尽管凯莱图完备码的众多结论已被给出,但鉴于课题的难度,这一问题还没有一个系统的、明确的解决方法.

LEE[11]证明了交换群的凯莱图存在完备码当且仅当它是一个完全图的覆盖,作为文章的一个应用LEE利用文献[11]中推论(集合S是完备码当且仅当S∩(X0+X0)={0}成立,其中X0是凯莱子集中的元素和单位元所组成的集合)证明了超立方体Qn存在完备码的等价条件.

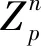
2 图的完备码和图覆盖

引理1 设G是一个有限群,S={s1,s2,…,sm}为G的Cayley图Cay(G,X)的一个完备码.则|G|=(|X|+1)m.

由完备码的定义可知,集合S内部的点之间无连边,对任意点v∈GS,有且仅有S中一个点与它相邻.再由凯莱图的定义可知,与集合S中每个点相连的顶点恰有|X|个,因此有|G|=(|X|+1)m成立.

引理2 设G是一个有限交换群,运算为加法,X={x1,x2,…,xn}为群G的一个Cayley子集,S={s1,s2,…,sm}为Cay(G,X)的一个完备码.则对任意i=1,2,…,n,S+xi={s1+xi,…,sm+xi}都是Cay(G,X)的完备码.

证明S+xi(i=1,2,…,n)是独立集.若否,假设存在sj,sk∈S,使得sj+xi～sk+xi,即存在某个xt∈X,使得sj+xi+xt=sk+xi,即sj+xt=sk,这与S是独立集矛盾.

任取点y∈G(S+xi),则S+xi中有且只有一个点与y相邻.否则假设存在st,sj∈S,使得st+xi～y且sj+xi～y.则存在2个点xa,xb∈X,使得y=st+xi+xa=sj+xi+xb,即st+xa=sj+xb,这与S是完备码矛盾.因此,S+xi中最多有一个点与y相邻.再由凯莱图的定义关系和S+xi是独立集可知,S+xi中恰好有一个点与y相邻,因此S+xi也是Cay(G,X)的完备码.

引理3[11]对于n∈,则下述条件等价:

(a)超立方体Qn存在完备码.

(b)n=2m-1,m∈.

(c)Qn是完全图Kn+1的正则覆盖.

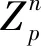
3 主要结果

引理3新证:

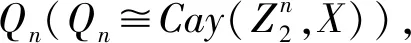
(b)⟹(a):设n=2m-1,m∈且m

对于任意的x,y∈W,若x与y相邻,不失一般性,假设x=y+ei,由超立方体图的定义知x与y只有第i个坐标位置不同,即x-y=(0,0,…,1,0,…,0),其中1位于第i个分量.由于x-y也是方程组的解,即H(x-y)T=0,因此矩阵H的第i列为零向量,这与H的列向量非零矛盾.这样,W是Qn的一个独立集.

我们将要证明对任意的x∈VW,有且仅有W中一个元素与它相邻.若存在y,z∈W,使x～y且x～z,由Cayley图的定义知,存在ei,ej,使得x=z+ei=y+ej成立.由超立方体图的定义知,x与z只有第i个分量不同,x与y只有第j个分量不同,则y-z=(0,0,…,1,…,1,0,…,0),其中两个1分别位于第i和第j个分量.由于y-z也是方程组的解,即H(y-z)T=0,因此矩阵H的第i列与第j列的和为零向量.因为运算是在二元域上进行的,所以H的第i列与第j列相等,这与H的列向量互不相同矛盾.这样,我们证明了W之外的任何一个点最多和W中的一个点相邻.再根据|W|=2n-m和W是独立集可知,W是Qn的一个完备码.

(a)⟹(c):假定Qn存在一个完备码S.设Kn+1的顶点集为{k0,k1,…,kn},定义超立方体Qn的顶点集到完全图Kn+1的顶点集的映射p,使得S→k0、(S+ei)→ki,其中i=1,2,…,n.下面证明p是一个正则覆盖.

由定义可以看出p是满射.由Cayley图的定义可知,S与S+ei中的点均有连边,s1～(s1+ei),…,sm～(sm+ei),i=1,2,…,n.对任意ei,ej∈X且ei≠ej,由引理2可得S+ei与S+ej均为Qn的完备码,所以S+ei中每个元素与S+ej中每个元素有且仅有一条连边,因此p是一个正则覆盖.

(c)⟹(a):假定Qn是Kn+1的正则覆盖,覆盖映射为p.对任意ki∈Kn+1,i=0,1,…,n,下面证明S=p-1(ki)为Qn的一个完备码.由正则覆盖的性质可知,S是一个独立集,且对任意点x∈QnS,S中有且仅有一个点与x相连,因此结论得证.

证明(必要性) 假定S是Cay(G,X)的完备码,由|G|=|S|(|X|+1)易知,存在m∈使得n=(pm-1)/2.

任取VW中一个向量δ,假设W中存在2个向量λ,μ都与δ在Cay(G,X)中相邻,不失一般性有2种情况.

(Ⅰ):假定λ-δ=ei,μ-δ=ej,其中1≤i≠j≤n.这时,H(λ-μ)T=H(ei-ej)T=0,这说明H中有两列相等,矛盾.

(Ⅱ):假定λ-δ=ei,δ-μ=ej,其中1≤i≠j≤n.这时H(λ-μ)T=H(ei+ej)T=0,说明H中的第i列和第j列互为负向量,这也与H的构造方式矛盾.

因此,VW中每一个向量最多和W中一个向量在Cay(G,X)中相邻.再根据|W|=pn-m和W是独立集易知,VW中每一个向量恰好和W中一个向量在Gay(G,X)中相邻,即W是Cay(G,X)的一个完备码.

证明与引理3新证中(a)⟺(c)类似.