基于VMD-MSE的高压断路器故障诊断

万书亭,马晓棣,豆龙江,周建平

(1.华北电力大学 机械工程系,河北 保定 071003; 2.国网浙江省电力公司 检修分公司,浙江 杭州 310004)

高压断路器作为电力系统中重要的保护与控制电器,其性能的可靠性对整个电网运行的安全具有重大意义.相关调查表明,高压断路器重大故障中有接近一半的故障是由于操作机构发生故障所引起的.因此,研究高压断路器操作机构机械特性对于提高断路器运行可靠性具有十分重要的意义[1-2].高压断路器分合闸过程中所产生的振动，包含了操作机构的状态信息.针对其振动信号展开分析,可发现断路器操作机构的故障信息,近年来已有大量文献提出利用振动信号对断路器进行故障诊断[3-5].实践证明:通过对高压断路器分合闸过程中产生的振动信号进行采集、提取和分析来对高压断路器进行故障诊断,是一种行之有效的方法.

断路器在分合闸操作中所产生的振动信号是典型的非线性、非平稳信号,夹杂着大量的噪声和干扰,很难提取到有效的故障特征信息,而现有的传统信号分析方法或多或少地存在着一些局限性和不足[6-9].熵是一种度量时间序列复杂度的非线性动力学参数,时间序列产生新模式的概率越大,其复杂度越高,熵值也越大[10].Pincus[11]提出了近似熵(Approximate Entropy,ApEn),ApEn通过比较数据和其自身来反映时间序列的复杂度,包含了自匹配.Richman[12]提出了样本熵(Sample Entropy,SpEn),SpEn作为ApEn的改进算法,降低了ApEn计入自身匹配引入的偏差,具有所需的数据短、抗噪和抗干扰能力强、在参数大取值范围内一致性好等特点[13].然而,ApEn和SpEn都是衡量时间序列单一尺度的复杂性,为了弥补单一尺度的不足,Costa等[14]提出了多尺度熵(Multiscale Entropy,MSE).MSE对时间序列进行空间尺度分割,计算各个尺度下时间序列的样本熵,得到时间序列在不同尺度下的复杂度.目前,MSE已经广泛应用到了故障诊断领域[15].变分模态分解(Variational Mode Decomposition,VMD)是Dragomiretskiy等[16]提出的一种信号处理新方法.该方法在获取本征模函数(Intrinsic Mode Function,IMF)分量时不同于经验模态分解(Empirical Mode Decomposition,EMD)算法和局部均值分解(Local Mean Decomposition,LMD)算法所使用的循环筛分剥离的信号处理方式,而是将信号分量的获取过程转移到变分框架内,通过构造并求解约束变分问题实现原始信号的分解,有效缓解或避免了EMD，LMD在递归模式分解过程中的模态混叠和边界效应等一系列问题,具有较高的运算效率以及良好的噪声鲁棒性[17].

由于高压断路器的振动信号是瞬时、非平稳的,且含有噪声,若仅采用MSE对其进行处理会影响特征量的准确性,同时为了解决EMD和LMD方法中存在的一系列不足,本文结合VMD和MSE,针对断路器振动信号非线性、非平稳的特点,提出了一种基于VMD-MSE的故障信号特征提取方法.

1 特征提取的理论研究

1.1 VMD的基本原理

VMD的分解过程即变分问题的构造和求解,其中变分问题的构造步骤如下:① 对每有一个模态分量,通过Hilbert变换,得到其解析信号;② 对各解析信号一个预估中心频率,将各解析信号的频谱变换到基频带上;③ 利用频移信号的高斯平滑指标估计各模态分量的带宽[18].

VMD的具体实现过程见文献[18].

1.2 MSE的基本原理

设原始数据为X={x1,x2,…,xN},长度为N,则MSE的具体计算步骤如下:

步骤1预先给定嵌入维数m、相似容限r及尺度因子τ=[1,2,…,τmax],对原始序列X进行粗粒化处理,建立新的粗粒向量，即

(5)

步骤2τ=1时,yi(1)就是原时间序列,对于非零,原始序列X被分割成τ段且每段长为N/τ的粗粒序列yi(τ).

步骤3计算每个粗粒序列的样本熵,即可得到MSE,样本熵算法见文献[12],

(6)

1.3 基于VMD-MSE的特征提取

基于断路器振动信号非线性、非平稳的特点,本文提出了一种基于VMD-MSE的断路器振动信号的特征提取方法,假设输入信号为X={x1,x2,…,xN},其中N为信号长度,基于VMD-MSE的特征提取方法的具体算法流程步骤如下:

步骤1使用VMD对输入信号进行分解,得到n个固有模态分量uk.

步骤2计算输入信号分解得到的各固有模态分量uk不同尺度下的样本熵,并将其进行组合,得到初始特征向量V.假设最大尺度因子τmax=m,则V为

(10)

式中:V的维度等于n×m;Enm为第n个模态分量计算得到的第m个尺度下熵值.

步骤3使用PCA[19]提取初始特征向量V的特征主成分Vm,Vm就是表征断路器振动信号特征的特征向量.

2 断路器振动信号特征提取

2.1 实验模型

为了验证所提出方法的有效性,本文以一台35 kV户外高压SF6断路器为实验对象.在断路器空载状态下,本文分别设置了3种模拟故障,并对正常状态及3种模拟故障状态下的断路器振动信号进行采集.其中,模拟故障分别为合闸弹簧疲劳、缓冲弹簧失效和基座螺栓松动.具体做法是调节合闸弹簧张紧力模拟合闸弹簧疲劳故障,摘除缓冲弹簧模拟缓冲弹簧失效故障,松动基座螺栓模拟基座螺栓松动故障.

本文选用江苏东华测试公司的1A102E型加速度传感器测量操作机构合闸过程中所产生的振动信号,该传感器量程为0～5 000 m/s2,频率响应范围为0.5～10 000 Hz.考虑到断路器合闸时间为(80±15) ms,设置采集时间为400 ms,采样频率为10 000 Hz,以保证振动信号的充分采集.考虑到断路器的振动主要来自弹簧操作机构和动、静触头的碰撞,加速度传感器安装在弹簧操作机构上,可以较好地获取断路器弹簧操作机构和动、静触头的振动响应.

2.2 特征提取

本文选取了所采集的断路器各运行状态20组振动信号作为样本信号,图1为断路器各运行状态合闸过程中所产生振动信号的时域波形.从图1中可以看出,各状态下断路器的时域信号没有明显的差异与变化规律.因此,需采用有效的特征提取方法从中提取特征参数,本文采用基于VMD-MSE的特征提取方法.

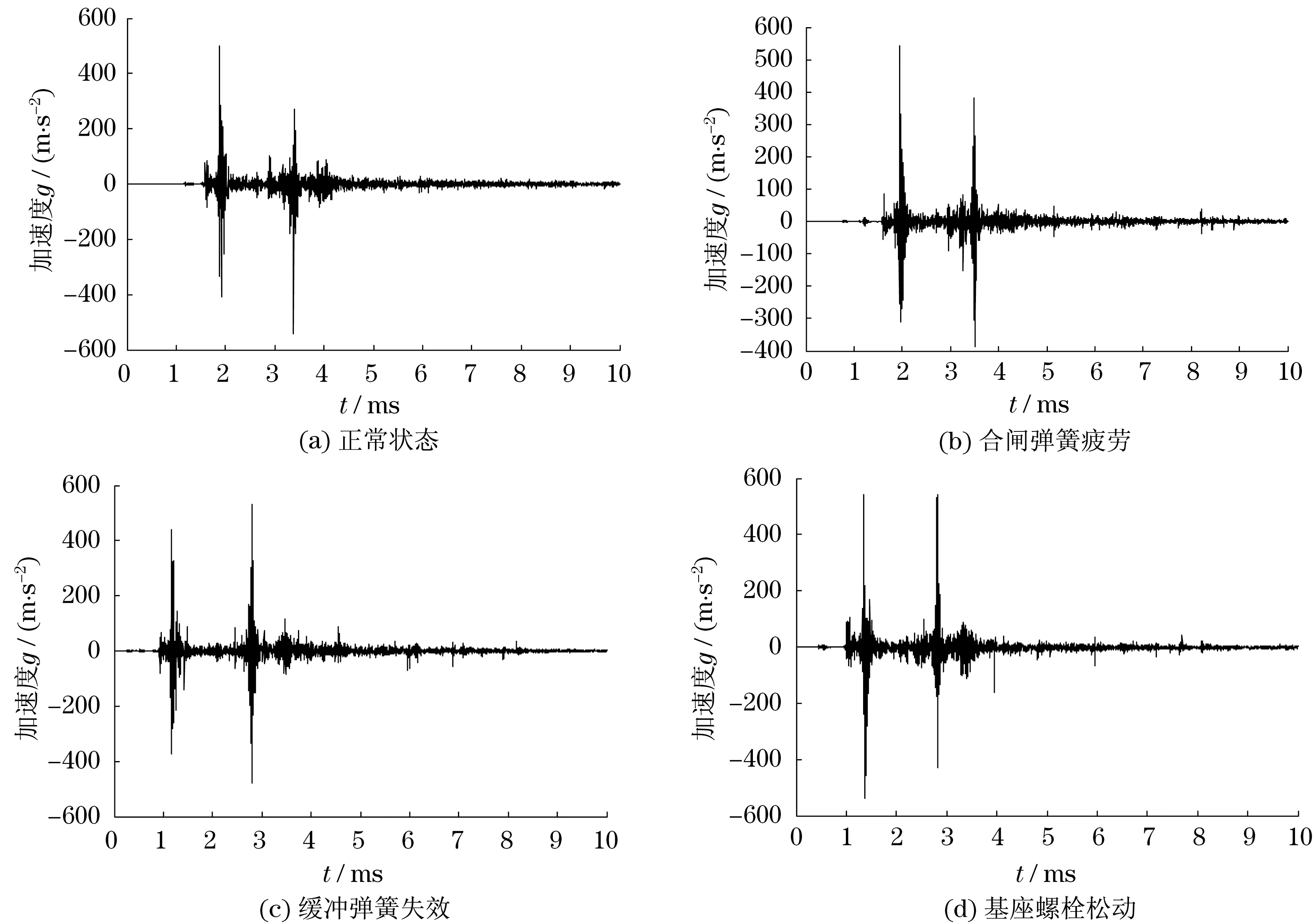
图1 振动信号时域波形Fig.1 Time-domain waveform of vibration signals

首先,使用VMD对输入信号进行分解.在使用VMD对原始信号进行分解时,需要预先设定惩罚因子α和分解模态数K.文献[20]提出根据采样频率fs预设惩罚因子α,并指明当惩罚因子α值越小,分解后所得到各个本征模态分量的带宽越大,容易出现中心频率重叠以及模态混叠的现象;惩罚因子α越大,则各本征模态分量的带宽越小,中心频率重叠以及模态混叠的现象消失,为保证不出现中心频率重叠以及模态混叠的现象,α应大于fs/2.本文为了保证计算精度与计算的时效性,取α为fs.

分解模态数K通过观察各个模态分量的中心频率及其与原始信号的相关系数确定.表1为选取某样本信号对应不同K值下的中心频率.

通过观察表1可以发现,当模态数K值过大时,出现了相近模态数.如K=7时,出现了379.9 Hz和398.8 Hz两个相近的模态数.

进一步分析不同K值下各模态分量与原始信号之间的相关系数,如表2所示.通过VMD分解后各模态与原始信号的相关系数分析,当K=7时,模态u3与原始信号之间的相关系数ρ1只有0.29,呈微相关;而当K=6时,各模态与原始信号的相关系数均大于0.3,呈实相关.

根据上述研究,本文首先预设初始分解数K=1,设定阈值c与θ.若分解后各模态与原信号之间的相关系数小于阈值c或前一模态的中心频率与后一模态的中心频率的比值小于阈值θ,则停止分解;反之令K=K+1,继续分解,直到满足条件停止.VMD分解流程：本文将阈值c设置为0.3,阈值θ设置为1.1.根据实验数据所得,本文VMD的分解数K为6.

表1 不同K值下VMD分解的中心频率Tab.1 The center frequency of VMD decomposition under different K

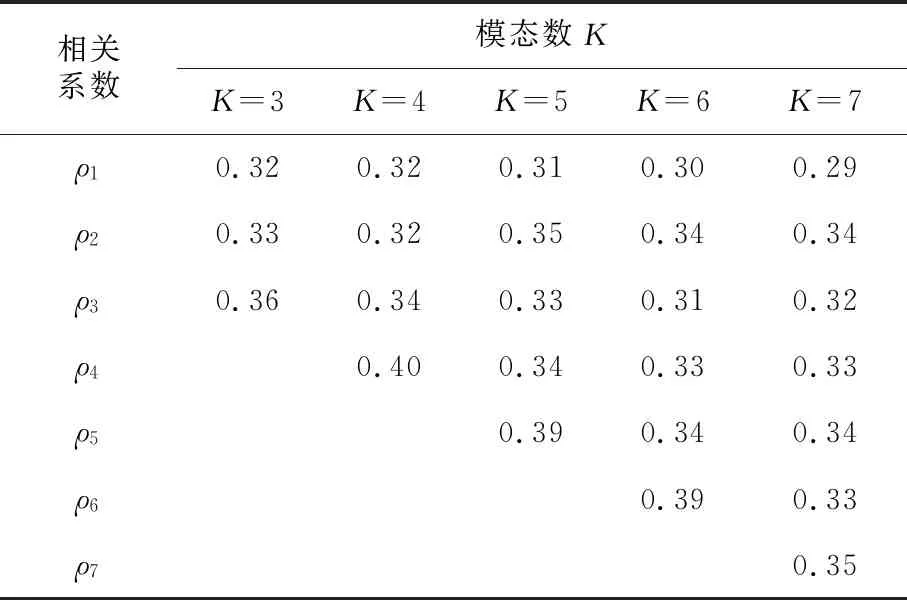
表2 不同K值下各模态分量与原始信号之间的相关系数Tab.2 The correlation coefficient between original signal and each mode under different K

计算各模态分量uk的MSE值.在使用MSE时,需要预先设定嵌入维数m、相似容限r和尺度因子τ.下面分别讨论上述参数的取值.

(1) 嵌入维数m.在序列的联合概率进行动态重构时,嵌入维数m越大就有越多的详细信息,但需要的数据长度也会随之增加[21].

(2) 相似容限r.相似容限r过大会丢失掉很多统计信息,r过小所得出的统计特性效果不理想,而且还会增加结果噪声的敏感性.一般情况下,相似容限r设置为0.10～0.25 SD,SD为样本数据的标准差[21].

(3) 尺度因子τ.过大的尺度因子τ会导致粗粒化后序列长度缩短,继而导致其熵值的精确度无法保证,所以尺度因子一般取τ=[1,20]即可.

通过数据对比,本文所使用的样本数据在m=2,r=0.15 SD和τ=[1,10]时,具有较好的区分度,将求解得到的MSE值进行组合,得到特征向量V,特征向量V的维度为60.

为了降低模式识别过程中计算的复杂度,提高分类器的诊断精度,利用PCA提取初始特征向量V中累计贡献率达到85%的特征主成分Vm.Vm即表征断路器振动信号特征的特征向量.

3 断路器振动信号的模式识别

断路器的工作特性决定了其本身不能频繁操作,实际实验采集的测试数据量有限,测试样本数较少不利于故障识别训练.传统的神经网络识别方法需要大量的测试样本,样本越多,最终识别越准确.由于支持向量机(Support Vector Machine,SVM)在解决小样本、非线性及高维模式识别中具有独特的优势,更适合断路器的故障识别,所以本文采用SVM来进行断路器的故障识别与分类,具体算法见文献[22].

选取各运行状态下共80组样本数据所提取的特征向量Vm,提取每种运行状态下的14组数据,共56组数据构建为训练样本集训练SVM分类器,剩余24组数据构建为测试样本集用于检验SVM分类器的性能.考虑到径向基函数(Radial Basis Function,RBF)模型简单,参数少,本文选用RBF函数作为核函数.另外,还需要设置惩罚参数C和g,经过实验对比,本文选择验证精度最高的参数C=4,g=0.1.测试样本的识别结果如图2所示,测试集中的24组数据分类结果与实际类别一致,说明利用训练好的SVM对测试样本进行分类测试,测试结果全部分类正确.

为了验证所提方法的优越性,本文同时设置了4组对照实验,分别为以基于原始信号和原始信号经过EMD分解后得到的模态分量的MSE,以及原始信号经过VMD分解后得到的模态分量的ApEn和SapEn作为特征向量,通过使用SVM进行训练和测试,识别结果如表3所示.其中,由于使用EMD对样本信号进行分解时分解层数过多,本文将根据各分解模态分量与原始信号的相关系数选取有效分量,相关系数阈值设置为c=0.3,以相关系数大于c的分量作为有效分量.经验证,经过EMD分解得到的前3个IMFs为有效分量.

图2 测试样本识别结果Fig.2 Recognition results of test samples

表3 对照实验的识别结果Tab.3 Recognition results of control experiment

由表3可知:以VMD分解得到的IMFs的MSE作为特征向量的正确识别率,高于以原始信号和EMD分解得到的IMFs的MSE作为特征向量的正确识别率.这是由于EMD等效于频域的一个高通滤波器和一系列的带通滤波器的输出,具有类似于二进制小波的频域分割性质.这种信号频域分割特性在处理故障信号时存在很大的弊端,在处理信号过程中,EMD方法自身的频域分割特性使得其在信号高频部分的分辨率过低,而具有带通滤波器组结构特性的VMD方法则能够弥补这一不足,实现信号高频部分的精细化分析[18].同时,以VMD方法得到的IMFs的MSE作为特征向量的正确识别率,高于以ApEn和SapEn作为特征向量的正确识别率.这是由于SpEn作为ApEn的改进算法降低了ApEn计入自身匹配引入的偏差,具有更强的抗噪和抗干扰能力,能够更好地表征振动信号的特征,而MSE可以在多个尺度上计算SapEn,包含了更多的信息.

4 结论

本文以高压断路器弹簧操作机构的振动信号为研究对象,采用基于VMD-MSE的特征提取方法对其进行特征提取,并采用SVM对断路器的4种运行状态进行分类,通过以上研究,得出以下结论:

(1) 以VMD-MSE的特征提取方法提取的特征向量相对其他提取方法所提取得到的特征向量具有更加明显的特征,分类结果更精确,可以准确、全面地反映高压断路器操作机构的运行状态.

(2) 对于断路器的振动信号,VMD和MSE参数的选取,目前尚没有一个明确的理论指导,基本上依赖于使用者的经验,而两者的参数选择会很大程度上影响断路器故障识别的结果.因此,需要更进一步深入研究和探索参数的选取方法,提高算法的分类精度和实用性.

(3) 通过PCA对原始特征集进行分析优化,可以大幅压缩特征向量的维数,去除冗余信息,从而降低故障模式识别中的计算复杂性,提高分类结果的精确度.

(4) SVM能准确地进行状态识别和分类,为断路器的故障诊断提供了一种故障模式识别的方法.