面向农机制造的供应商协同物料配送策略
杨晓英,程攀攀
(河南科技大学 机电工程学院,河南 洛阳 471003)
随着农业现代化和生产集约化的推进,农业生产各领域在加快推进“机器换人”,促进农机行业向全程化、大型化、智能化转变,这对农业机械化供给侧的能力、质量和效率提出了新的更高要求.如何顺应新形势、新需求,以创新发展为驱动,快速响应市场需求,提供客户满意的产品与服务,在市场中取得竞争优势,成为我国农机制造企业生存和发展面临的重要问题.供应商是企业获得竞争力的重要资源,供应商物料配送的准时化和标准化不足问题,一直是制约农机企业生产的瓶颈,供应商物料配送如何与制造企业生产协同成为企业快速响应市场需求的关键.因此,研究面向农机制造的供应商协同物料配送策略,对提升农业供给侧能力具有重要意义.
关于供应商物料配送问题的研究一直是国内外学者研究的热点.当前具有代表性的研究成果有:李毅鹏等[1]从多供应商的视角来研究如何通过供应商之间形成零部件横向协同,向制造商齐套供应零部件,从而降低制造商的期望总库存成本;戢守峰等[2]研究了由供应商、分销商和零售商组成的多级供应链中基于协同计划、预测与补货(Collaborative Planning Forecasting and Replenishment,CPFR)的协同补货问题;于渝飞等[3-4]建立了面向订单装配(Assemble to Order,ATO)系统中多供应商-单制造商的零部件协同供货模型;方忠民等[5-6]建立了以供应链中核心生产企业为主方,供应商为从方的Stackelberg博弈-协同模型,有效降低供应链系统成本.为了减少库存成本并提高服务水平,制造商不断以准时制原则组织供应商物料配送[7-8].Zhang等[9-10]研究了需求随机条件下供应商订货量分配问题,确定了供应商的最优供货时间决策和制造商最优的库存责任期设置;Low等[11-12]提出以最小化运输成本为目标的非线性数学模型确定供应商最优配送批量;马士华等[13-14]研究了在supply-hub运作模式下供应商协同补货策略,确定了供应商的最佳配送批量以及补货次数等.
以上研究对供应商供货策略、物料配送期量等方面做出了很大贡献,对于研究供应商协同物料配送具有重要借鉴意义,但是针对农机制造多供应商配送多物料至核心制造商的“M-N-1”物料配送模式下,协同产品生产计划的供应商动态物料配送期量模型研究较少.因此,本文针对农机制造生产特征,以拖拉机生产为研究对象,从降低供应商、制造商总成本的视角,采用精益化与协同化理念提出多供应商协同物料配送策略,建立供应商协同物料配送期量优化模型,为供应商物料配送标准化、准时化、快速响应生产需求提供理论依据.
1 问题提出
1.1 现状分析
供应商物料配送问题可以看作是由一个核心制造商、多个供应商所组成的供应链系统.精准化的供应链是供应商必须按照生产顺序计划需求,准时准量配送物料至制造商,避免高库存和缺货停线.农机企业为了满足不同地域、环境、作业需求生产选配不同的机型,导致农机装备机型多、物料品种多.以拖拉机为例,物料品种繁多,同种物料通常由多家供应商按比例供应,每家供应商同时供应多种物料,属于“M-N-1”物料配送模式,如图1所示.当前供应商与制造商生产之间的协同度较低,供应商通常采取大批量少频次方式进行物料配送,导致物料配送准时率、准确率降低,增加了制造商库存成本与物料管理难度,影响了企业的效率和效益.

图1 供应商物料配送模式Fig.1 Mode of supplier material delivery
1.2 问题分析
当前多供应商配送多物料至核心制造商的“M-N-1”物料配送模式,缺乏协同物料配送的期量标准,即规范每个供应商配送物料的时间和数量,该期量与制造商生产计划协同,且与农机企业淡旺季明显的生产特征相适应.因此,制订多供应商与制造商生产计划协同的物料配送策略D(T,Q)是关键,其中配送期量(T,Q)的优化模型是核心,为供应商与制造商实现物料配送智能决策、信息实时和物流协同奠定理论基础.
为此,考虑影响供应商物料配送效率的影响因素,以降低制造商、供应商总成本为目标,建立基于模糊软时间窗的供应商协同物料配送期量优化模型,运用仿真优化确定物料配送期量,保证供应商物料配送的准时率和准确率.
2 供应商协同物料配送期量模型
2.1 模糊软时间窗
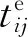
式中:Tij为供应商i配送物料j的实际到达时间.
2.2 配送期量优化模型
(1) 优化目标.供应商物料配送期量同时影响供应商配送成本与制造商库存维持成本,物料到货时间又是制约配送期量的关键因素.因此,该模型的优化目标包括3个部分:供应商配送成本、供应商时间惩罚成本、制造商库存维持成本,通过保证3种成本最小化,确定供应商物料配送期量.
(2) 约束条件.① 供应商单次配送量不大于运输车辆的最大运载量与制造商的最大库存量;② 根据制造商的物料需求,供应商按供货比例将物料分为批次配送,配送总量必须满足生产需求;③ 各供应商批次到达时间根据生产计划顺序确定,车辆配送一次结束后返回供应商等待下次配送,每家供应商至少一辆运输车辆;④ 制造商生产所需的每种物料至少保证由一家供应商配送,且每家供应商至少配送一种物料.
目标函数为
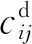
该模型中式(1)为目标函数,包括供应商配送成本、制造商库存维持成本和供应商时间惩罚成本;式(2)表示供应商单次配送量满足车辆、库存约束;式(3)和式(4)表示各供应商总配送量满足生产需求;式(5)保证每种物料到货时间满足生产需求;式(6)和式(7)保证每种物料至少有一家供应商,每家供应商至少配送一种物料.
3 模型求解
基于模糊软时间窗的供应商协同物料配送模型是一类不确定条件下(包括随机和模糊)的多项式数学规划问题,制造商的生产计划具有动态不确定性,供应商协同制造商需求快速确定物料配送计划.运用算法求解需要将问题简化为可重复迭代的递归过程便于求解,但是过程过于复杂,且求解结果的实际可操作性差,为了保证求解结果的实际应用性强,本文运用仿真进行求解.
供应商物料配送问题主要由单次配送量和配送时间两个部分组成,关键是将数学模型参数嵌入仿真模型,供应商物料配送的仿真处理流程如图2所示.

图2 仿真流程Fig.2 Simulation flow
(1) 需求信息整合.需求信息来源于制造商生产计划,作为该模型的输入参数对需求信息进行整合用矩阵M表示,矩阵M作为仿真系统的顺序控制表指挥各模块按照需求序列运行.其中,集合x={1,2,…,m}表示物料集合,集合y={1,2,…,n}表示供应商点集合,集合z={Q11,Q12,…,Qij}表示物料需求量集合,集合t={t11,t12,…,tij}表示物料需求时间集合.
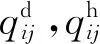
(3) 变量优化.供应商物料配送量、配送时间作为变量需要在仿真模型中进行初始定义,仿真模型中变量作为Program的输入是确定优化方案的决策因素.供应商物料配送方案的产生、筛选与变量密切相关,采用“二分法”与轮盘赌算法优化配送方案,具体步骤如下.

步骤2采用轮盘赌方法产生初始方案,φ11=u1,u1∈[0,ωij],采用二分法方案产生区间变为[0,u1]∪[u1,ωij].不同的区间分别采用轮盘赌反复迭代产生新的配送方案φij,并不断根据新方案利用二分法划分区间,直到区间不可再分停止迭代.
步骤3为了加快最优方案的收敛速度,对方案进行初步筛选.为了降低供应商的配送成本,运输车辆的装载率η=[0.7,1.0],每家供应商每天配送次数λij={3,8},当配送次数λij相等时,φij=min{φk},筛选后的配送方案fij={f1,f2,…,fk}.
步骤4输出设置.为了便于分析输入参数对仿真结果的影响,将目标函数通过优化设置响应变量.目标函数优化为C=C1+C2+C3,其中,C1为供应商配送成本,C2为制造商库存维持成本,C3为供应商时间惩罚成本.通过仿真运行对比不同配送方案fij的总成本,输出总成本最小的方案为最优方案.
4 实例应用
本文以某拖拉机制造的供应商物料配送为例,根据按照基于模糊软时间窗的供应商协同物料配送模型,对供应商的物料配送期量标准进行仿真优化.通过仿真运行不同供应商物料配送方案,对仿真结果进行对比分析,在保证供应链总成本最低的条件下,逐步确定供应商最优配送方案.
4.1 案例背景
在拖拉机某日生产需求中选取5家供应商配送6种物料为例,各供应商与物料的需求信息如表1所示.

表1 供应商和物料需求信息Tab.1 Supplier and material requirement information
系统仿真的目标是在保证供应商准时化物料配送的前提下,保证供应商、制造商的总成本最低,以多供应商物料配送为对象,建立仿真模型如图3所示,建立5个资源对象作为供应商,每个资源存放订单及物料需求时间,建立6个实体作为6种不同物料,建立1个储存器和1个消耗器分别表示制造商仓库和生产装配线,规定资源对象和实体同时满足且与储存器需求序列一致时订单完成.
4.2 仿真结果分析
仿真每次运行8 h,通过仿真运行产生16种可行方案,每种方案的平均车辆满载率为0.83~0.92,方案中包括各供应商的配送量、车辆平均满载率、方案总成本,运行结果如表2所示.对仿真结果进行对比分析,逐步确定供应商物料配送的最优方案.
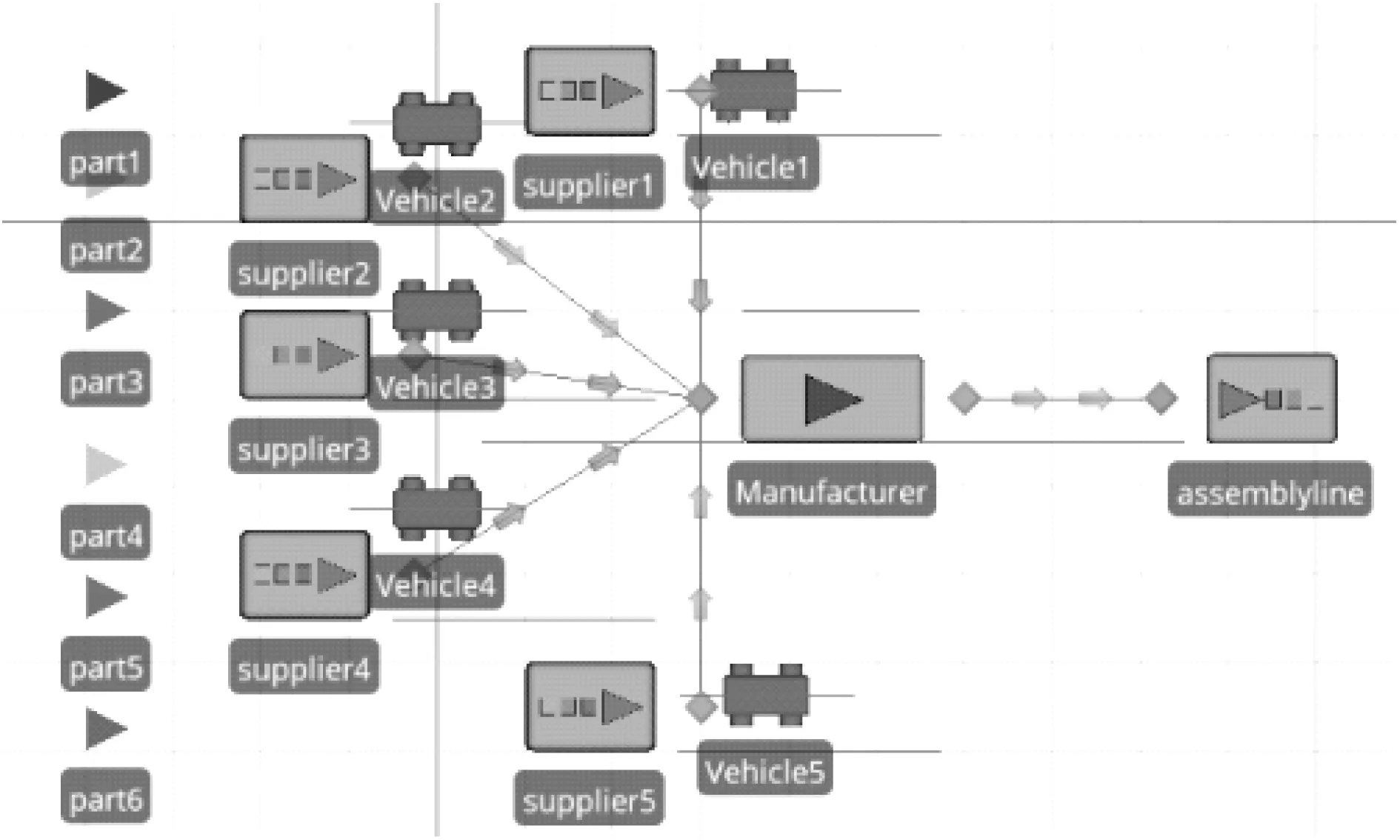
图3 案例仿真模型Fig.3 Simulation model
4.3 效果评价
由上述分析可知,方案11为最优方案,总成本最低为5 997.5元,车辆平均满载率为83%.根据最佳配送量可知各供应商的配送频次、车辆满载率,最优配送方案如表3所示.
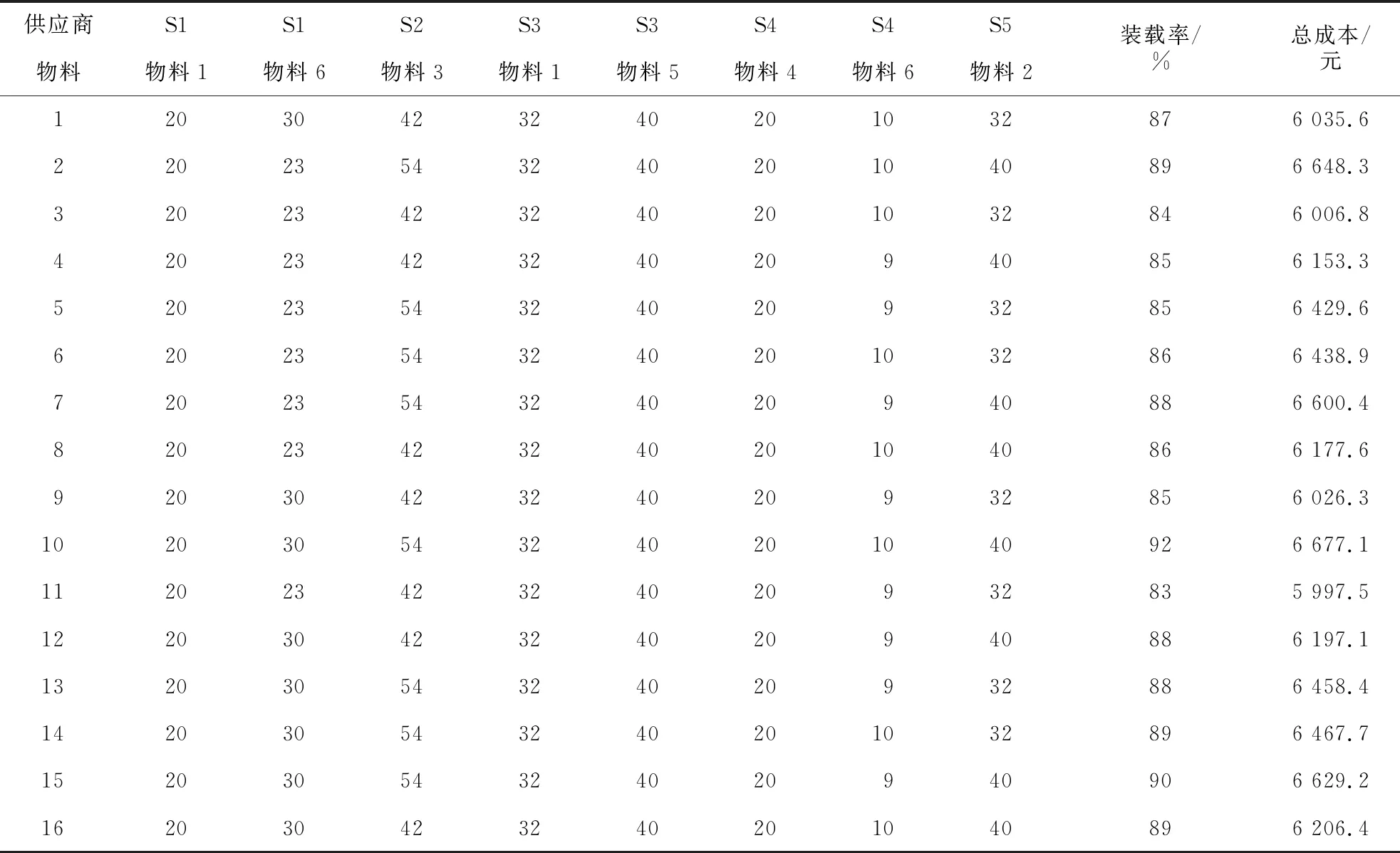
表2 仿真运行结果Tab.2 Simulation results

表3 最优配送方案Tab.3 Optimal result
供应商物料配送期量在保证车辆满载率的前提下有效避免供应商大批量配送现象,简化了供应商物料配送流程,降低了供应商、制造商的总成本,提高了供应商物料配送的准时率与准确率,对农机制造业实现供应商物料配送精准化具有重要意义.
5 结语
本文针对多供应商配送多物料至核心制造商的“M-N-1”物料配送模式,结合农机制造农机企业淡旺季明显的生产特征及物料需求的动态性,提出了一种多供应商协同制造商生产计划的物料配送策略,可有效避免制造商的缺货停线损失,提高了物料配送的精准率,降低供应商、制造商总成本,建立了基于模糊软时间窗的供应商协同物料配送期量优化模型,增强了供应商与制造商的协同性.以某拖拉机为例,运用仿真优化逐步寻优,确定了物料配送期量,验证了该方法的有效性和可行性.

