一种新型捣固装置及参数确定方法
刘云山
(1.辽宁轨道交通职业学院 机械工程系,辽宁 沈阳 110023; 2.东北大学 机械工程与自动化学院,辽宁 沈阳 110819)
捣固机属于小型铁路养护机械,因其机动灵活,常应用在大型养路机械不便应用的线路,如在线路曲率半径太小或支线等情况下的施工.
本文研究新型液压捣固机的激振与捣固装置及参数确定方法[1],提出了捣固装置动力学参数的确定方法.不同于传统液压捣固机的激振与捣固装置,为提高捣固机的捣固作业质量和效率提供了一条新的有效途径.
1 激振方式
1.1 捣固机械的激振方式
目前我国捣固机械激振方式有两种:一种是以偏心块转动,产生离心力而带动捣固镐振动;一种以偏心轴转动,通过曲柄连杆机构带动捣固镐振动(即所谓强迫振动)[2].
捣固机以偏心块转动产生离心力为振动源进行道床捣固,液压缸同步夹实,目前使用的电动捣固(DZG-350,DDJ-300型等)和小型液压捣固机(YD-1,YD-2,XYD-1型等)均采用这种振动形式.液压捣固机为双导柱框架结构,单缸升降方式.
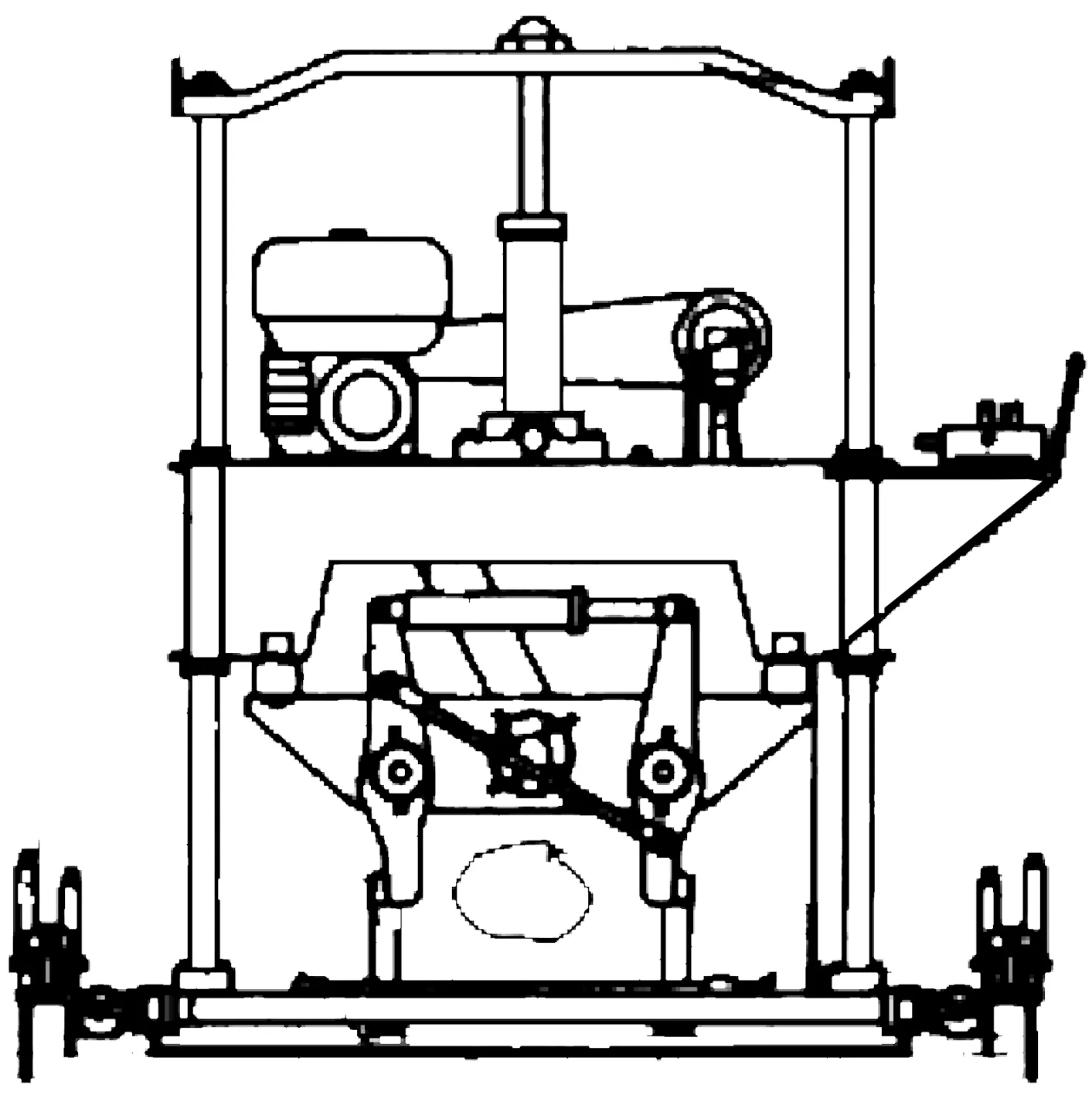
图1 偏心块式液压捣固机示意图Fig.1 Schematic diagram of eccentric block hydraulic tamping machine
采用偏心轴转动,通过连杆带动捣固镐振动(即所谓强迫振动),再加上异步夹实,是国内外大型捣固机普遍采用的振动方式.它具有固定的振幅,能有效地将动力传递给镐头;镐头的拨动力能随着道床阻力的增大而增大,而且可以实现反相捣固,有利于捣实枕底道碴[4].在实际捣固过程中大型捣固机通过内外加持油缸进行加持动作,因两侧捣固镐所受的道床阻力不同,侧捣固镐坚持移动距离也有所不同,所以是异步夹持.这种异步夹持动作,能够使枕底石砟密实度均匀[5].
大型捣固车采用的是强迫振动和异步夹实的原理,捣固镐对道碴的作用是摇摆式振动和夹实,但功率大,结构复杂,造价昂贵,不适于铁路日常频繁的小规模维护保养.对此,专利[6-7]将强迫振动方式应用于小型液压捣固机上,但存在的主要问题是由于刚性连接,振动幅值不能调节,因而在需要调整振动幅值的场合应用不方便.文献[8]指出,在板结道床要求低振动幅值,在松散道床需要高振动幅值.而且在捣固机理方面,利用振动波理论提出了一种推论:在初始的振动、捣固次数增加时,道碴的密实度有所提高,道碴密实度提高到一定程度后,随着振动、捣固次数的增加,道碴密实度反而减小.由此可见,在道碴足够密实,捣固力足够大时,振幅不减小反而降低捣固效果.
1.2 新型捣固机的激振方式
针对现有捣固机传统偏心块转动式激振方式和强迫振动式激振方式的不足,本新型捣固机在设计上提出了一种新型的基于弹性连杆理论的强迫振动式反相位激振与捣固装置,其目的是既能解决传统捣固机不能实现反相位振动和异步夹持的问题,又能克服传统强迫振动激振方式的振动幅值不能调节问题,提高捣固效果,使捣固机的应用更加灵活.
2 新型捣固机捣固装置的结构及工作原理
2.1 新型捣固机捣固装置的结构
新型捣固机捣固装置由偏心装置、夹持装置和弹性连杆装置组成(见图2).偏心装置由带轮、主轴、偏心轴承、主轴轴承座组成;夹实装置由液压缸、螺纹活塞连杆组成.弹性连杆装置由下弹簧、弹簧固定螺纹板、弹簧安装板、弹簧安装板固定螺栓、上弹簧组成.
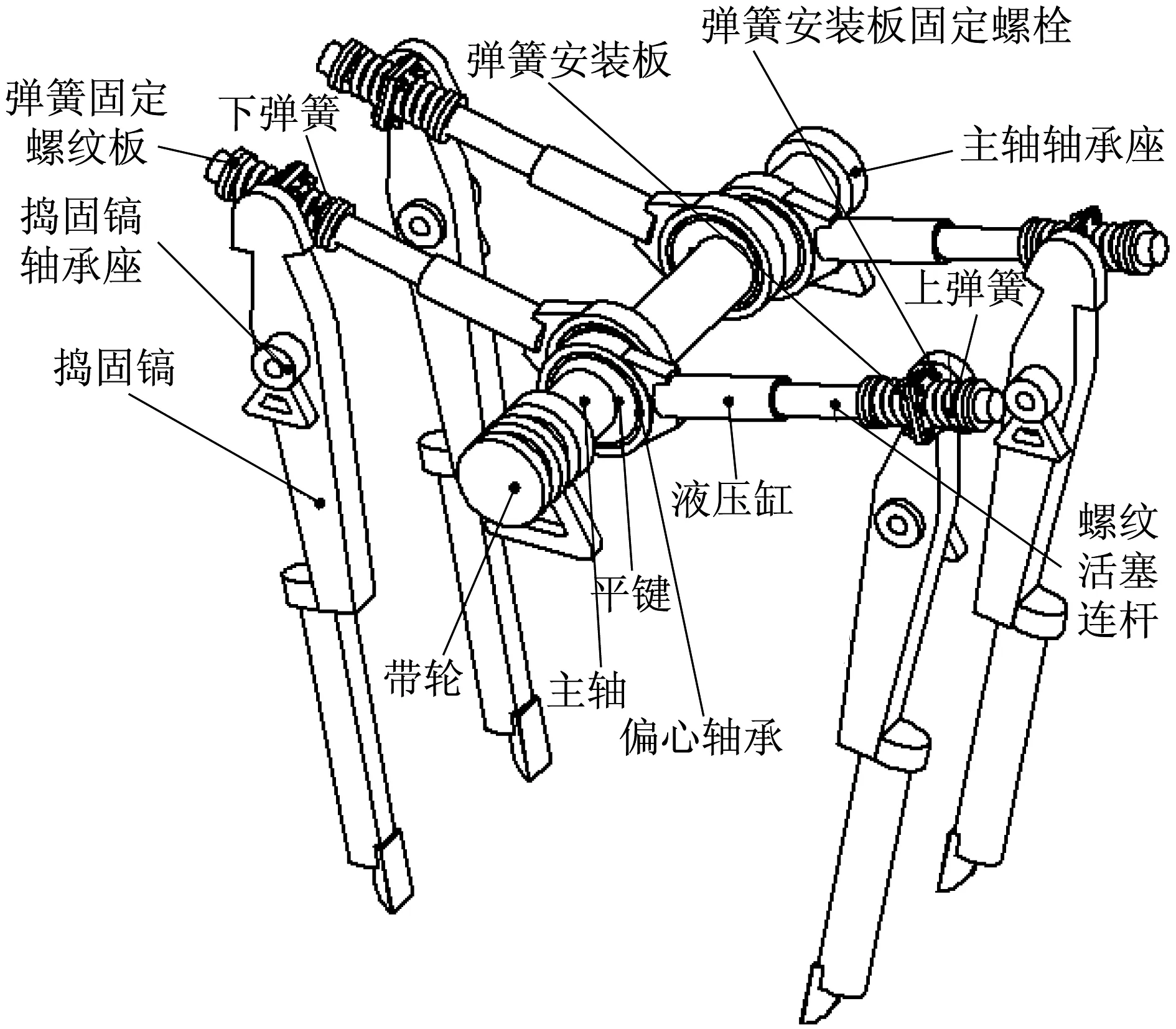
图2 新型捣固装置结构三维示意图Fig.2 Three-dimensional structure diagram of the structure of a new tamping device
2.2 新型捣固机捣固装置的工作原理
图2中,主轴由内燃机通过皮带传动提供动力,绕轴心顺时针转动.偏心轴承由于偏心安装在主轴上的原因,其偏心距相当于弹性连杆机构的曲柄长度.在液压缸与活塞杆没有相对位移时,液压缸与螺纹活塞连杆整体相当于弹性连杆机构的连杆.由于偏心距的原因,当主轴旋转时,弹簧在连杆一端产生位移,弹簧产生形变,这样就产生了弹力,弹力作用于捣固镐上,就使捣固镐产生左右摆动式的强迫振动.由于两侧偏心轴承相位相差180°安装主轴上,捣固镐振动的相位也就相差180°,实现反相捣固,有利于捣实枕底道碴.考虑振动频率较高,振动状态设为非共振状态,要求主轴圆频率为振动系统固有频率的3~5倍.这就是单质体弹性连杆式振动设计理论的应用.
当液压系统驱动两侧的液压缸使活塞杆与液压缸有相对运动时,相当于增大或减小了弹性连杆的连杆长度,会导致两捣固镐绕两捣固镐轴承座,有较大的转动,产生夹持动作.通过设计液压传动系统可以实现异步夹持,能自动应对道碴两侧的不同阻力,有效地将石碴重新密实排列于枕轨之下.
(3)注重系统的稳定性与开放性。平台依附于企业级服务器,系统稳定运行的情况下,尽可能减少和杜绝系统漏洞,在此基础上丰富系统功能,全面改进稳定性,形成客户端技术层面上的与用户需求相贴合的体验。
3 新型捣固装置动力学参数确定方法
3.1 新型捣固装置动力学模型
建立捣固装置中除去夹持装置的动力学模型.图3为动力学模型,属于单质体弹性连杆式摆动振动模型.该模型由偏心部分、连杆部分和振动质体部分组成.偏心部分为一个半径为r的圆,r表示偏心装置中偏心轴承的偏心距,圆心代表偏心装置中的主轴,设转速为ω,转动方向为顺时针.连杆部分由一条直线段和一个弹簧力学模型组成:直线段代表弹性连杆装置中的螺纹连杆,其一端连接偏心部分的圆的圆周上一点,另一端连接一个弹簧力学模型,该弹簧力学模型轴线与所述连杆部分直线段重合;弹簧力学模型代表弹性连杆装置中的弹簧,设弹簧刚度为k,其另一端连接所述振动质体部分(捣固镐).
所述振动质体部分为一条长度为(l+h)的直线段,代表弹性连杆装置中的捣固镐,即振动质体.该直线段与所述连杆部分直线段夹角大于70°小于90°,其一端与所述连杆部分弹簧力学模型相连,设相连点为A点;另一端为自由端,设该端为D点;在沿所述振动质体部分直线段与A点距离为l处为捣固镐转动轴心,设该点为B点,即所述振动质体部分直线可绕B点在所述偏心部分的圆所在平面内转动;在沿所述振动质体部分直线段与B点距离为p处为C点,该点代表捣固镐质心.
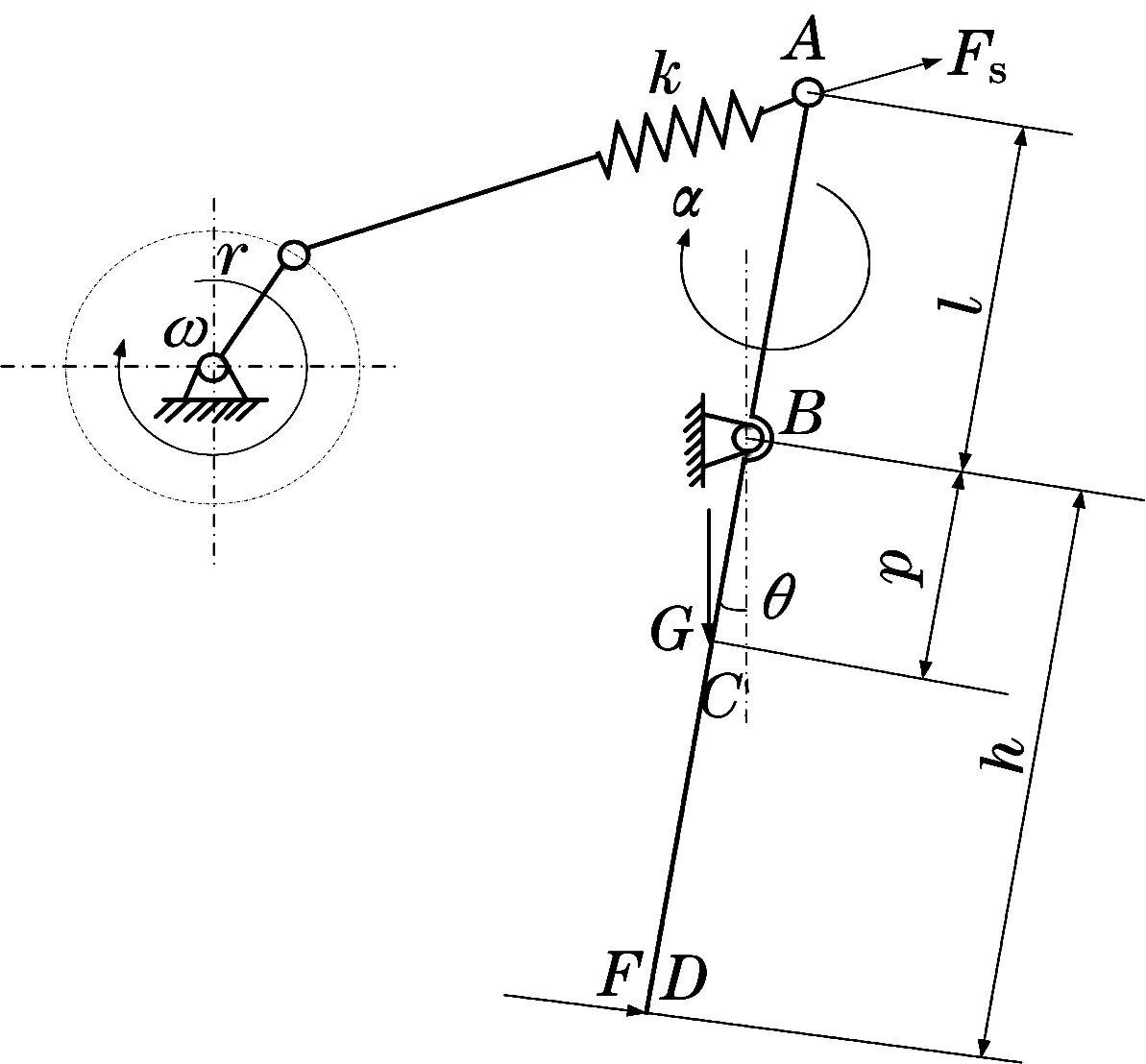
图3 单侧捣固臂动力学模型Fig.3 Dynamic model of one-side tamping arm
3.2 新型捣固装置动力学参数确定方法
设捣固镐所受重力大小为G,作用点为C点,方向竖直向下;设捣固镐所受弹簧弹力大小为Fs,作用于A点,方向沿所述振动质体部分的直线段的轴线;设捣固镐所受石料的反力在垂直于捣固镐方向的分力,即捣固力,为F,作用于D点,方向垂直于所述振动质体部分直线的轴线;设其所受阻尼力对B点的力矩大小与捣固镐转速成正比的比例系数,即总阻尼系数,为f,其方向为阻碍捣固镐转动趋势的方向;设捣固镐相对于轴承座B点的计算转动惯量为J;设振动的平衡位置为所述振动质体部分直线段竖直时的位置.
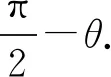
设石料参与振动部分的结合质量为ms,则石料惯性力就是捣固力F,其大小为
(1)
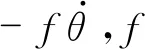
(2)
动力学模型中θ很小,将其进行线性化处理,即sinθ≈θ,cosθ≈1.将其带入式(2),再将式(1)带入式(2),则上述方程化简为
(3)
为标准的振动微分方程,其特解(即强迫振动位移θ的解)为
(4)
式中:A为捣固镐振动的单侧角度参量的振幅;t为时间变量;α为角位移落后于名义激振力矩klsin(ωt)的相位差角.
msh2可视为物料结合质量对B点的转动惯量.将式(4)带入式(3),解得A的表达式为
(5)
α的表达式为
(6)
其中,z0为频率比,即工作频率ω与固有频率ω0之比
(7)
而ω0为系统固有频率,
(8)
ζ为阻尼比,即
(9)
设其激振端(A点)振幅为λ,则
(10)
由式(5)~式(10),可推得本装置设计参数的确定方法:根据工程需要与工作条件确定基本参数λ,ω,z0,ζ与ms的值.再进行捣固镐部分的初步结构设计,捣固镐的结构设计完成后确定J,G,p,l与h的大小.
由式(7)推得固有频率ω0为
(11)
由式(8)推得弹簧刚度k为
(12)
由式(5)与式(10)推得偏心距r为
(13)
捣固端(D点)的振幅为角参量振幅A乘上捣固端到捣固镐B点的距离h.从式(5)可以看出,k值改变,A即改变,捣固端振幅即改变.
通过更换弹簧,改变弹簧刚度k,就可以改变捣固镐的振幅,这也是本捣固装置与传统捣固机相比的一大优势.
3.3 新型捣固装置动力学参数确定方法实例
本发明实例的设计参数如下:λ=0.75 mm,ω=293.215 rad/s,z0=4,ζ=0.05,ms=2.326 kg,J=0.565 kg·m2,G=130.124 N,p=0.119 m,l=0.245 m,h=0.490 m.
将上述数据带入式(11)~式(13),算得偏心距r=11 mm,弹簧刚度k=100 226.037 N/m.
4 结语
新型液压捣固机的激振与捣固装置工作原理新颖、结构简单,适用于情况复杂的石砟道床.单质体弹性连杆式振动设计理论的应用,解决了现有捣固机的传统偏心块式激振方式和强迫振动式激振方式的不足.新型捣固机动力学参数确定方法,为液压捣固机的激振与捣固装置的设计提供了可靠的理论依据.
——有效的抗弓形虫药物靶标

