巧妙导入,事半功倍
——以《正弦定理》为例
陈园园 瑞安市第七中学 325211
常言道“好的开始是成功的一半”,然而“万事开头难 ”,一节数学课要想在有限的四十分钟内最大限度地吸引学生的注意力,激发学生的学习兴趣,获得理想的教学效果,就要抓好新课导入这一环节。然而教学没有固定的形式,一堂课如何开头,也没有固定的方法。由于教育对象不同,教学内容不同,每堂课的开头也必然不同。即使是同一教学内容,不同的教师也有不同的处理方法,获得的教学效果也都是不同的。下面,笔者结合自己的教学实践,针对高中数学必修五第一章解三角形中的《正弦定理》这一节新课做导入方面的设计探究。
一、温故知新,自然导入
孔子曰:“温故而知新,可以为师矣。”此高度肯定了温故对于知新的作用,教师完全可以将这种作用运用到高中数学课堂新课导入中来,利用数学新、旧知识之间的联系,既复习巩固了旧知识,又联系了新知识,使知识能够由浅入深、 由简单到复杂地向高一层次发展,有利于启发学生思维,降低学生对新知识的认知难度,使学生从旧知识的复习中自然获得新知识。
比如在讲解《正弦定理》一课时,可以先引导学生回顾:任意三角形中的边与角有怎样的关系?在学生回答出任意三角形中角与角、边与边以及边与角之间的关系之后,再进行提问:我们是否能得到这个边、角关系准确量化的表示呢?也就是说任意三角形中的角A、B、C和边a、b、c之间有怎样的数量关系呢?这就是我们接下来要研究的问题,这样的引入,自然流畅,找到学生的逻辑起点,从学生的最近发展区出发,学生明显能感受到新知是在已有旧知基础上的延伸和拓展,能有效促进学生对新知的理解和掌握。教师应当重视这种方法的作用,备课时悉心研究教材,找到新旧知识内在而非表面的联系,并努力巧妙融合、创新应用,让知识的过渡显得浑然天成。
二、开门见山,直接导入
顾名思义,就是采用较为直接的方式,教师紧扣教学目标,直接从课本的课题中提出新课的学习重点、难点和教学目的,立即会引起学生的注意,诱发学生探求新知识的兴趣,使学生直接进入学习状态。
比如在讲解《正弦定理》一课时,教师可以直接导入:今天,我们要进一步学习任意三角形中边与角关系的有关知识——正弦定理。(板书课题)这样的导入直接明确了本节课的主题,使学生对本节课的学习任务清晰明了,促使学生迅速集中到新知识的探索追求中。但这种导入方式一般用于一些新授的数学知识难以借助旧知识引入时使用,既提高课堂效率,又能唤起学生的注意。而用在此处看似直截了当,但过于枯燥乏味,没有考虑到教学效果。
三、创设情境,设疑导入
亚里士多德有一句名言:思维起于疑问。因此,学生学习数学知识时,只有在不断地发现问题、分析问题与解决问题的循环中锤炼,才能高效地获得学习成果。所以,在导入中,教师创设富于趣味的生活情境,设置疑问引发思考,可以极大的激发学生的探究欲望,从而产生了对新知学习的强烈兴趣,使学生获取的知识印象更加深刻,对学生的学习是极有帮助的。
比如在讲解《正弦定理》一课时,教师可以创设情境如下:(1)在我国古代就有嫦娥奔月的神话故事.明月高悬,我们仰望夜空,会有无限遐想,不禁会问,遥不可及的月亮离我们地球究竟有多远呢?科学家们是怎样测出来的呢?(2)桂林山水甲天下,假设A,B两点在河的两岸, 只给你米尺和量角设备,不过河的话,你可以测出它们之间的距离吗?这样用贴近学生生活实际或为学生所喜闻乐见的情境导入,将新课知识置于生活情境之中,使学生感到亲切、自然,有效激发了学生的学习兴趣,而且通过设疑的方式,有利于把现实问题向数学问题转化,让学生更加真实地领会到数学带来的乐趣,感受到数学源于生活,又服务于生活。
四、观察发现,探索导入
罗丹说过:“生活中从不缺少美,而是缺少发现美的眼睛。”美不是空谈,而是要去观察、去发现、去探索,数学中的美也是一样。教师要引导学生从一些数学现象中善于发现其中的规律,从而顺利导入新课,此种方式可以让学生在观察与发现的过程中获得喜悦,从而提高学习的动力和积极性,同时也会增强对新知识的消化与理解。
比如在讲解《正弦定理》一课时,教师可以让学生探究:对于含30°的直角三角形,观察三边与对应的三角函数,你能发现什么?

边 a=1 b=images/BZ_96_1681_1863_1732_1908.pngc=2 sinA= sinB= sinC=cosA= cosB= cosC=tanA= tanB=不存在三角函数A=30°B=60°C=90°
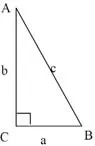
引导学生从特殊的含30°的直角三角形中观察出正弦定理的关系式,这样导入新课可使学生在发现的喜悦中提高学习的兴趣,同时也有利于学生对新知识的理解和记忆,然后教师引导学生将得到的发现引向严密的逻辑推理,进一步探索并证明在一般三角形中正弦定理仍然成立。这样对教材来说,这是一种自然的过渡,对学生来说,则成为一种思维上的需要和满足。当然这样导入适用于那些容易发现的规律。
俗话说:“教学有法,教无定法。”高中数学课堂中新课导入的方法多种多样,教师在实际教学过程中,切忌照本宣科,死搬硬套,一定要结合教学实际和学生需求,针对不同的教学内容,根据自己的教学风格,灵活选用导入方法,从而使枯燥乏味,抽象晦涩的数学课堂变得趣味横生,让学生在数学新课之初就萌生浓厚的对新知识的好奇,从而自觉主动地进入数学知识的学习进程中,这样的数学课堂才会是高效的课堂,我们的教学也才会收到事半功倍的效果。

