鱼眼镜头光学系统的非球面优化设计

张 潇，吕丽军

(上海大学 精密仪器系，上海 200444)

引言

鱼眼镜头的视场角一般可以达到180°甚至270°[1]，能同时获取很大视场范围的场景图像。由于鱼眼镜头系统大视场成像光束以很大斜入角照射在光学元件表面，偏离近轴成像，导致严重的像差。非球面光学元件可以有效地消除像差，提高成像质量[2]。常用的确定非球面的方法是无像差法，但该方法为了实现稳定的高精度测量，对人员要求和操作环境要求较高。利用三坐标测量仪获得坐标，然后进行最小二乘曲面拟合[3]，从而降低了对人员和环境的要求，但计算量很大。研究如何选择系统中哪个光学面为非球面及确定非球面面型是十分有意义的。

对于鱼眼镜头光学系统，大视场物点发出的光束以很大的入射角度入射到前组负弯月形透镜的表面，其成像具有平面对称的特性。赛德尔像差理论不再适合此类系统的分析[4-8]。非球面的光路计算考虑通过迭代逼近真实光路情况[9]，缺陷在于很难提出一个适合于各种场合逼近精度的数值判据。目前，LU等应用波像差的方法发展了平面对称光学系统的像差理论[10]，并基于此理论发展了超大视场光学系统的优化设计方法，最近，进一步发展了适用于超大视场光学系统的六阶波像差理论[11]，可对大孔径鱼眼镜头系统进行像差分析计算。本文在这些工作的基础上，推导了二次圆锥曲面的面型系数，建立了五阶像差的评价函数，针对一个全球面鱼眼镜头，应用六阶波像差理论，分析各光学面的波像差分布以及它们随非球面系数的变化趋势，从而选定应用非球面的光学表面，并使用自适应归一化实数编码遗传算法(ANRCGA)[12]对其进行优化。

本文简要介绍了六阶波像差理论，推导了适用于该理论的面型系数公式，分析其与波像差的关系，并建立基于五阶像差的评价函数，以便以数值方式评价优化设计。提出了如何为鱼眼镜头光学系统选择合适的光学面为非球面的方法，对所提出的方法进行数值验证，并对结果进行比较分析。

1 波像差理论

1.1 平面对称光学系统的像差计算

对由g个光学面组成的平面对称光学系统，系统的波像差是各光学面的波像差之和，即：

(1)

式中：W(k)、nk和wij0(k)分别表示第k个光学面的波像差、折射率和波像差系数；xk和yk表示光线入射在第k个光学面上的孔径坐标。若将最后一个光学面上光线的孔径坐标(xg,yg)作为参考坐标，上式也可写成[11]：

(2)

式中：nk/g=nk/ng；Ak/g和gk/g分别为在第k和第g光学面之间x、y坐标的线性传递系数。

波像差理论研究超大视场光学系统时，在全视场范围内取多个视场物点，分别计算各视场物点的波像差，然后求和来反映光学系统在整个视场范围的成像性能[10]。因此，对像差的贡献占主导地位的波像差是球差波像差Wsph、彗差波像差Wcoma和场曲波像差Wcurv。其中场曲是通过光学面的出射波阵面和参考波阵面的几何关系得出的[13]，计算公式如下：

Wsph=W400x4+W220x2y2+W040y4+W600x6+

W420x4y2+W240x2y4+W060y6

(3)

Wcoma=W300x3+W120xy2+W500x5+

W320x3y2+W140xy4

(4)

(5)

一般鱼眼镜头后光组的光瞳尺寸比前光组的大很多，因此，Wsph和Wcoma的主要贡献来自于后光组光学面。另外，大视场物点发出的光束以较大的斜入射角入射到前组光学面上，所以场曲的主要贡献来自于前光组的光学面。

通过对波像差关于子午和弧矢方向分别求导，得到光线在像面上的五阶像差(x′,y′)表达式为

(6)

式中dij0和hij0为像差系数[11]。

从上述表达式可以发现，波像差和像差都受到面型系数ci,j的影响，因此可以通过cij控制波像差，提高成像质量。鱼眼镜头光学系统的孔径一般较大，参考文献[10]所述四阶精度不够精确，还需推导适用于六阶波像差理论的面型系数。

1.2 二次圆锥曲面的面型系数

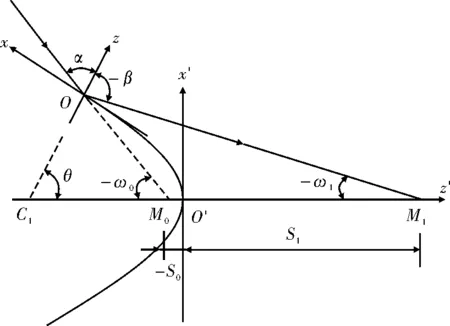
图1 主光线经过二次圆锥曲面反射时坐标系统xyz的原点(主光线和光学面的交点)坐标Fig.1 Origin (intersection of chief ray and optical surface) coordinates of xyz coordinate system when chief ray is reflected by quadratic conical surface

如图1所示，在以光学面和光轴的交点O′为坐标原点的坐标系x′y′z′，绕z′轴旋转的二次圆锥曲面方程为

x′2+y′2=a1z′+a2z′2,a1=2R0

(7)

式中：R0是二次圆锥曲面在O′点处的曲率半径；a2是二次圆锥曲面的非球面系数，当a2=-1时该曲面为球面，当a2≠-1时为非球面。

波像差理论中描述面型时采用以光线与光学面交点O为原点的坐标系xyz，因此将常规的二次圆锥曲面方程式(1)转换到坐标系xyz中，x轴为原点O沿光学面的切线，y轴为原点O沿光学面的法线，y轴的斜率为tanθ。根据图1所示，坐标系x′y′z′和坐标系xyz的转化关系为

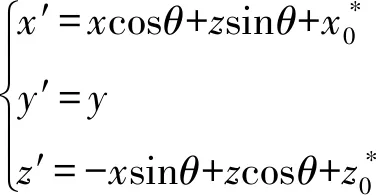
(8)

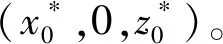
将(8)式带入(7)式，并作泰勒级数展开，就可以得到适用于六阶波像差理论的二次圆锥曲面方程：

z=c2,0x2+c0,2y2+c3.0x3+c1,2xy2+c4,0x4+

c0,4y4+c2,2x2y2+c5,0x5+c3,2x3y2+c1,4xy4+

c6,0x6+c4,2x4y2+c2,4x2y4+c0,6y6

(9)

式中ci,j为各阶对应的面型系数，具体表达式如下：

c2,0=-a21B3c0,2=-1Bc3,0=-4Aa21x∗0B6c1,2=-4Ax∗0B4c4,0=-a21(a21C2+16A2X∗20)B9c0,4=-C3B5c2,2=-2(a21C2+8A2x∗20)B7c5,0=-4Aa21x∗0(3a21C2+16A2x∗20)B12c1,4=-12AC2x∗0B8c3,2=-8Ax∗0(3a21C2+8A2x∗20)B10c6,0=-2a21[a41C4+16A2x∗20(3a21C2+8A2x∗20)]B12c4,2=-2[3a41C4+32A2x∗20(3a21C2+4A2x∗20)]B13C2,4=-6C2(a21C2+16A2x∗20)B11c0,6=-2C2B9

虽然波像差表达式中各项参数都受到面型系数ci,j的影响，但是每一个光学面的面型影响成像质量的程度不一样。从以上公式可知，ci,j受a1和非球面系数a2影响，a1=2R0，所以a2是影响ci,j的主要因素，通过a2改变ci,j，进而影响波像差。

2 利用非球面优化鱼眼镜头

2.1 评价函数的定义

为了对鱼眼镜头光学系统进行数值评价，在视场范围内取k个视场物点，基于它们在像面上的像差点列图分布，定义鱼眼镜头光学系统的像差评价函数为

(10)

其中，

式中：εi表示不同视场角的权重因子；Wq和L分别为光束在最后光学面上沿子午(x)和弧矢(y)方向的投影长度；x′和y′为光线在像面上的像差，可由(6)式计算得到。(10)式中积分域采用椭圆是因为孔径光阑一般采用圆形孔，但光束在子午和弧矢平面内的焦点位置不一样，从而造成光束截面一般呈椭圆形。

2.2 应用非球面的优化思路

利用非球面优化鱼眼镜头的基本思路是，找到系统中对成像质量影响最大的光学面，利用非球面系数a2减小其波像差。对于一个光学系统来说，光学面的波像差越大，其各类光学参量对加工制造的精度要求越高[14]。因此选择波像差最大的光学面为非球面，在减小波像差、提高成像质量的同时，也有助于增大非球面的可允许公差范围，降低非球面的制造难度。

对鱼眼镜头系统各视场的物点而言，主要影响成像质量的是各光学面的球差波像差Wsph和彗差波像差Wcoma及前光组的场曲波像差Wcurv。大孔径时各光学面的Wsph和Wcoma对像差的贡献远大于Wcurv，分析波像差分布，选择波像差较大的光学面为非球面。若几个光学面的波像差均较大，则需进一步结合系统总的波像差情况，分析各光学面Wsph和Wcoma随非球面系数a2的变化趋势。假设系统总的球差和彗差波像差符号相反，应该选择Wsph和Wcoma随a2的变化趋势相反的光学面；若系统总的球差和彗差波像差符号相同，则应选择Wsph和Wcoma随a2变化相同的光学面。另外，如果有多个光学面符合上述条件，则选择随a2变化最迅速的光学面，以减小加工难度。小孔径时，Wcurv对像差的贡献大于各光学面的Wsph和Wcoma。结合之前的研究[15]，本文认为选择第1和第3光学面为非球面可以有效校正场曲。

确定非球面后，利用评价函数式(9)和自适应归一化实数编码遗传算法(ANRCGA)[12]，得到评价函数最优时的非球面系数值及相应的光学系统参数。

3 数值验证

3.1 鱼眼镜头实例

应用上述方法，对专利文献[16]中的鱼眼镜头进行优化设计，其光路如图2所示，工作波段为可见光，最大半视场角ω0=80°。分别进行如下5种情况的分析比对：1) 对专利设计进行全球面优化设计；2) 取较大孔径(F#3.3)时后光组的非球面设计；3) 取较小孔径(F#7.6)时后光组的非球面设计；4) 取较大孔径(F#3.3)时，前光组第1、3光学面的非球面优化；5)取较小孔径(F#7.6)时，前光组第1、3光学面的非球面优化。表1为上述5种情况优化后的光学参数，其中：rk表示光学面的曲率半径;dk表示镜片间距。表2为5种设计对应的非球面所在光学面及系统接收孔径。

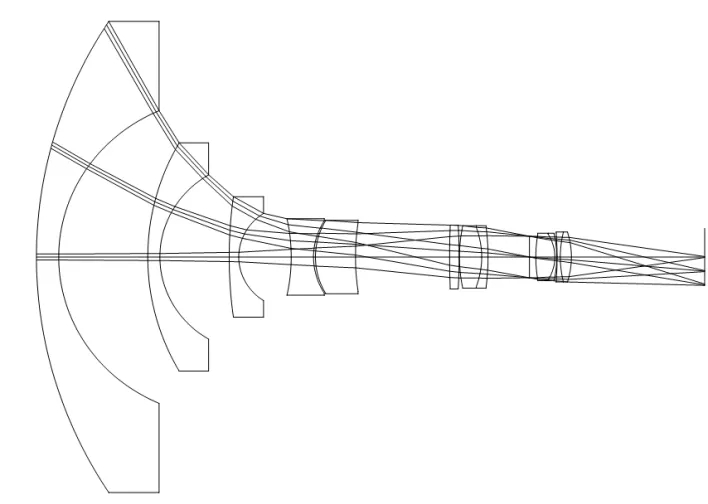
图2 鱼眼镜头光学系统光路图Fig. 2 Optical path of fisheye lens

表1 鱼眼镜头Design x的光学参量 mm

表2 Design x的非球面所在光学面及a2

根据以上所述，由(3)式计算专利原始设计0°，10°，…，80°共9个视场的波像差Wcurv、Wsph和Wcoma，取ω0=80°时波像差的分布，如图3所示。其中图3 (a)和图3(c)分别为F#3.3和F#7.6时各光学面波像差分布情况，图3(b)为系统的前组场曲波像差。∑k为系统总的球差波像差∑Wsph和彗差波像差∑Wcoma。由于系统前5个光学面的Wsph和Wcoma均小于0.01，图3中未列出。

图4(a)、(b)和(c)分别为当第17、18和21面为非球面时，该光学面的Wsph和Wcoma随非球面系数a2的变化趋势。

图3 鱼眼镜头的波像差分布Fig. 3 Wave aberration distribution of fisheye lens

图4 Wsph和Wcoma随第k个光学面a2的变化趋势图Fig. 4 Changing trend of the k-th surface’s Wsph和 Wcoma with aspherical coefficient

根据图3和图4可知：

1) 第8、9、17、18和21光学面的波像差比较突出，但是第8和第9面曲率半径相似且空气间隔很小，两者的波像差大小基本相同，符号相反，可以相互抵消，不纳入非球面的考虑范围。

2) 由于系统的∑Wsph和∑Wcoma同号，从优化角度考虑，要求光学面Wsph和Wcoma随 变化趋势相同。在第17、18和19面中，只有第17面符合条件。

3) 当大孔径F#3.3时，Wcurv相对较小，应优先校正Wsph和Wcoma，选择第17面为非球面；当小孔径F#7.6时，Wcurv的作用显著，应优先校正前光组场曲，选择第1和3面为非球面。

3.2 优化与讨论

确定待优化的光学面后，对5种情况依次应用(9)式计算出对应的评价函数，令εi=1，将该光学面的非球面系数a2遍历[-4,4](涵盖了常见的易于加工的非球面类型[17])，变化步距为0.01。选择使评价函数达到最小时的a2为相应的非球面系数初值。

基于评价函数，将(9)式中60°、70°和80°这3个视场角的权重因子εi取为5，其他权重因子εi取为1。然后应用自适应归一化实数编码遗传算法(ANRCGA)[12]分别对5种情况进行全局优化。种群数为300，每一代种群规模为100，交叉概率为0.85。采取粗、精两轮优化，粗优20次，各光学参量的优化搜索范围为其初值的±50%；从中选择评价函数最小的5次作为精优的初值，搜索范围取初值的±20%，所有视场的物点均为无限远。图5为优化后5种设计在ω0=0°，ω0=40°和ω0=80°时的点列图，图中坐标为Image width，单位为μm。表3为它们的评价函数Q，图6为Design 2和Design5的波像差分布。

图5 不同视场角时最后成像面上的孔径光线像差(最右侧一列参数表示视场角)Fig. 5 Aperture ray aberrations on final image plane at different field angles (The far right column parameter means field angles)

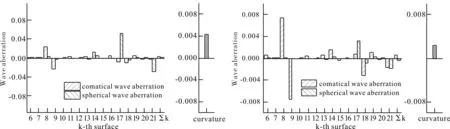
图6 Design 2和Design 5波像差分布图Fig. 6 Wave aberration distribution of Design 2 and 5

表3 鱼眼镜头的评价函数值

分析图5和表3可以得出如下结论：

1) 4种非球面优化设计比全球面优化设计Design 1的点列图的范围减小1/2，评价函数值提高了约1个数量级，说明ANRCGA算法可用于鱼眼镜头的非球面优化，且效果良好。

2) 小孔径时的Design 4和Design 5比大孔径时的Design 2和Design 3的评价函数值小。说明本文建立的评价函数可以准确反映鱼眼镜头光学系统的成像质量。

3) Design 2的结果优于Design 3，说明在大孔径系统中，按照各光学面的波像差分布，选择波像差较大且对非球面系数敏感的光学面为非球面，可以有效校正系统的波像差，并改善镜头成像质量。

4) Design 5的结果优于Design 4，说明随着孔径的减小，各光学面的Wsph和Wcoma减小，Wcurv的作用显著。此时Design 4优化Wsph和Wcoma的效果不如Design 5优化前光组Wcurv，因此在小孔径光学系统中应该优先校正场曲波像差。

5) 当孔径较大时，Design 2优化效果显著；孔径较小时，Design 5优化效果显著。比较图6与图4可以看出，经非球面优化后Design 2的Wsph和Wcoma大幅降低，Design 5的Wcurv大幅降低，说明本文提出的优化方法有效。

4 结论

推导了适用于六阶波像差理论的面型方程，分析了波像差与光学面面型的关系，提出了一种有效选择非球面的方法。对验证实例系统来说，当系统的F#7.6，前组的场曲波像差较大时，选择对场曲波像差影响较大的第1和3光学面为非球面；当系统的F#3.3，各光学面的球差和彗差波像差较大，根据系统的波像差分布情况，选择波像差较大，且随a2的变化趋势有助于系统两类总的波像差减小的光学面(第17面)为非球面。通过实例证明，本文提出的方法可以快速选出非球面，对利用非球面优化鱼眼镜头有借鉴意义。