利用目标和大气偏振信息的雾天图像重构方法

张 强，高 隽，范之国，王振武，闫 羽

(合肥工业大学 计算机与信息学院，安徽 合肥 230601)

引言

在雾、霾大气中悬浮着大量的微小颗粒，这些微小颗粒具有非常强的散射效应，使得成像系统获取的图像模糊不清，成像效果严重降质[1-3]。因此，研究雾、霾天气下清晰成像的方法，具有十分重要的应用价值。偏振成像作为一种新兴的光学成像技术，已经在光学遥感、军事侦察和医学诊断上得到了广泛应用。相对于传统光学成像，偏振成像不仅可以获得目标的颜色和强度信息，还可以获得环境和目标的偏振信息[4]。利用偏振信息可以对雾天图像进行重构，实现图像清晰化处理。

针对雾天图像模糊不清的问题，国内外学者做了大量的研究工作，主要包括两类：一类是非偏振的单幅图像去雾方法，比较经典的有Tan和He的去雾方法。Tan[5]基于无雾图像的对比度比有雾图像对比度要高的现象，通过最大化局部对比度，实现了单幅图像的去雾。He[6]提出了一种基于暗通道先验的单幅图像去雾方法，利用暗通道先验方法，可以估计出大气传输图，利用细化修补后的大气传输图可重构出目标图像。另一类是偏振去雾方法，Schechner[7-9]提出了基于差分成像的偏振去雾算法，其认为大气光为部分偏振光，而目标光为非偏振光。利用获取的同一场景下的偏振差分图像，估算大气光偏振信息，通过人工选取天空区域，估计无穷远处大气光强，最后利用雾天成像模型恢复出目标图像。非偏振去雾方法包括图像增强和图像复原两方面，图像增强不考虑图像退化的机理，只提高目标对比度，但对目标细节的复原能力有限。图像复原通过建立大气散射模型，对造成图像质量下降的影响因素进行估计，并反演退化过程，复原目标图像。但是，该方法对模型参数的估计仅依据图像强度信息，相关参数估计方法也存在局限性，复原的目标图像容易出现噪声斑块。偏振去雾方法不仅可以获取图像的强度信息，还可以获取偏振信息，增加了去雾模型的信息维度。太阳光经大气散射，形成部分偏振光；不仅大气光具有偏振特性，目标光也具有偏振特性。目标光的偏振态不仅与大气中微粒的散射作用有关，还与目标本身材质，表面粗糙度有关。因此，大气光偏振特性和目标光偏振特性存在差异。针对目标光偏振特性和大气光偏振特性的差异，提出了一种利用目标偏振信息和大气偏振信息的雾天图像重构方法。首先，从光强图像中，初步分离出大气光图像和目标光图像，利用大气光图像和目标光图像，解析大气光偏振态和目标光偏振态，再根据偏振信息估计相关参数，最终重构出目标图像。

1 雾天偏振图像重构模型

在雾、霾等天气条件下，大气中悬浮着大量微小颗粒，大气光和目标光在传播过程中，会与大气中悬浮的微小颗粒接触产生散射作用。大气光与悬浮的微粒散射后变成部分偏振光，大气光到达成像系统的偏振态与大气中微粒浓度、大小、成像距离有关。目标光的偏振态不仅与大气中微粒的散射作用有关，还与目标本身材质，表面粗糙度有关，不同的目标到达成像系统的偏振态不同。因此，成像系统探测到的偏振信息不仅包含了大气光的偏振信息，还包含了目标光的偏振信息。但是，应该考虑大气光偏振信息和目标光偏振信息存在的差异性。雾天偏振成像模型如图1所示。

其数学表达式可描述为

I=D+A

(1)

IP=DP+AP

(2)

IP=IP

(3)

式中：I表示成像系统获得的总光强；D表示目标光强；A为大气光强；IP表示成像系统获得的总偏振光强；DP表示目标偏振光；AP表示大气偏振光；DP和AP存在差异。

根据偏振度的定义：

DP=DPD

(4)

AP=APA

(5)

式中：P表示总光强偏振度；PD表示目标光偏振度；PA表示大气光偏振度。将 (3)、(4)、(5) 式代入 (2) 式可得

IP=DPD+APA

(6)

联立 (1) 式和(6) 式，在目标光图像和大气光图像中，分别建立DP和AP的解析式：

(7)

(8)

根据大气散射模型[10-12]D和A的数学表达式分别为

D=JT(x)

(9)

A=A∞(1-T(x))

(10)

式中：J表示目标表面反射光光强，即为目标图像；T(x)表示大气传输率；A∞为无穷远处大气光强。由(1)、(9)、(10)式，消去大气传输率T(x)，可得到雾天成像模型的表达式为

(11)

将 (7)、(8) 式代入雾天成像模型(11)可得雾天偏振图像重构模型的表达式

(12)

文中提出的雾天偏振图像重构模型是在大气散射模型的基础上，引入了目标光和大气光的偏振信息，增加了模型的信息维度。在构建偏振去雾模型时，考虑了彼此偏振信息的差异性，分别在大气光图像和目标光图像中解析大气光偏振信息和目标光偏振信息。 (12) 式中,总光强I和偏振度P可由偏振图像直接计算得出，所以偏振图像重构模型中，只要估算目标光偏振度PD，大气光偏振度PA和无穷远处大气光强A∞，即可重构出目标图像J。

2 模型参数估计

2.1 估算大气光偏振度和目标光偏振度

估算大气光偏振度PA和目标光偏振度PD，需要从获得的偏振图像中初步分离出大气光图像A和目标光图像D，并分别在大气光图像和目标光图像中计算出大气光偏振度PA和目标光偏振度PD。

现有估算大气光的方法有暗原色先验[6]和中值滤波方式[13]，暗原色先验方法无法处理天空区域以及景物亮度和天空接近的区域；中值滤波具有一定的滤波效果，但是，一定程度上会造成去雾后图像的边缘细节丢失。针对以上问题本文采用一种融合图像梯度信息的高斯滤波方法来估算大气光强和目标光强。

高斯滤波(Gaussian blur, GB)是一种根据正态分布来分配权值的线性平滑滤波器。相对于均值滤波器和中值滤波器，高斯滤波器引入了空间距离因子，对滤波窗口内的像素计算权重，越位于窗口外侧的像素权重越低，其对待处理像素的影响就越小，位于窗口内侧的像素与待处理像素更接近，权重更高。高斯滤波数学表达式如下

(13)

(14)

式中：ωg是高斯模板即权重矩阵；x和y表示周边像素相对于中心像素的相对坐标；δ表示模糊半径即权重矩阵的大小；I表示待滤波图像；Ω为开窗区域。

由于高斯滤波只考虑了图像像素的空间距离，没有考虑图像梯度信息，因此高斯滤波实际上是一种低通滤波器，会让图像低频部分通过，滤除高频部分。对于图像梯度变化快的部分，高斯滤波容易丢失图像细节，造成图像边缘模糊。

在高斯滤波进行权重分配时，引入图像梯度信息即梯度相似度因子，与空间距离因子相结合构成新的权重分配函数，融合图像梯度信息的高斯滤波(GB′)的数学表达式如下

(15)

(16)

(17)

式中：dg表示x与y之间的梯度距离；ωd为x与y之间的梯度相似性。

采用上述滤波函数对偏振图像I0、I60、I120分别进行差分滤波处理，得到大气光偏振图像A0、A60、A120，滤波公式如下:

(18)

获得A0、A60、A120后，根据 (1) 式可得出目标光偏振图像D0、D60、D120:

(19)

由此，可根据Stokes矢量公式在大气光图像A内计算大气光偏振度PA：

(20)

(21)

同理，也可在目标光图像D内计算大气光偏振度PD。

2.2 估算无穷远处大气光强

现有去雾方法中，无穷远处大气光强通常认为是雾天图像中最亮的像素值或者人工选取图像中天空区域某一点的强度值，作为整幅图像无穷远处的大气光强值，这种方法均存在一定的偶然性。选取图像中最亮的像素值作为无穷远处大气光强容易受到噪声点和白色建筑物等目标的干扰，使估计的无穷远处大气光强值偏高，而选取图像中天空区域某一点的强度值作为无穷远处大气光强的方法必须要求包含天空区域。

文中无穷远处大气光强A∞的估算在大气光图像A内进行，在大气光图像A空间内估算无穷远处大气光强 ，可有效避免大气光图像D内白色建筑物等高亮度目标的干扰。对大气光图像A取图像块Ω，对图像块Ω内的有效像素点计算标准差σ。通过3σ法则阈值分割，求Z(x,y)二值化矩阵：

Z(x,y)=

(22)

式中：Z(x,y)为经过3σ法则阈值分割的二值化矩阵；A(x,y)表示Ω内坐标为(x,y)的像素点；Ω为3×3的图像块；σ表示图像块Ω内像素点的标准差。

归零化图像块Ω内异常像素点的灰度值：

(23)

得到的A′(x,y)为去除噪声点和高亮度目标像素点的图像块Ω，在对图像块Ω内的像素作最大值滤波，得到图像块Ω内亮度最高的像素值作为无穷远处大气光A∞的估计值：

(24)

为了分析估算结果受噪声的影响，与现有亮原色方法[11]进行定量对比分析。本文方法和亮原色方法估算无穷远处大气光强结果如图2所示。

图2 无穷远处大气光强估算结果Fig.2 Estimation of atmospheric light intensity at infinity

图2中(a)、(b)、(c)为原始偏振图像，(d)为亮原色方法估算无穷远处大气光图像，(e)为本文方法估算无穷远处大气光图像。原始偏振图像中建筑物表面白色反射光会对无穷远处大气光图像的估算产生干扰。亮原色方法估算结果受目标干扰明显，图像中目标轮廓突出，建筑物表面反射光在亮原色方法中直接判别为无穷远处大气光强。采用3σ法则阈值分割结合最大值滤波的方法，在大气光图像A空间内估算无穷远处大气光强。首先，在大气光图像A空间内估算无穷远处大气光强，可有效避免白色建筑物等高亮度目标的干扰，通过3σ法则阈值分割可进一步剔除图像中的异常噪声点，降低残留噪声对无穷远处大气光估算结果的影响。最后，通过最大值滤波方法得到每一像素点处的无穷远处大气光强值。

为了定量分析本文方法估算结果，引入平均梯度和边缘强度作为定量评价标准。图2中无穷远处大气光图像的定量评价结果如表1所示。

表1 实验结果定量评价

平均梯度和边缘强度分别反映图像对比度和图像层次，值越大表明无穷远处大气光的估算结果受目标和噪声的影响越大。通过定量对比分析可知，本文方法估算结果的平均梯度和边缘强度远远低于亮原色方法估算结果，说明本文方法可有效避免白色建筑物等高亮度目标的干扰，降低图像噪声对估算结果的影响。

3 实验结果分析

采用已经标定的三通道偏振测量系统[14-15]搭建实验平台，开展雾天偏振图像采集实验。三通道偏振测量系统通过棱镜分光的方法，可以同时获得一个场景下的0°、60°、120°的雾天偏振图像。系统工作波段为380 nm ～1 000 nm，分辨率为1 392×1 040像素。实验结果如图3所示，图中烟囱距离相机3.7 km，其中图3(a)、(b)、(c)分别为三通道偏振测量系统采集的0°、60°、120°雾天偏振图像。图3(d)、(e)是大气光图像A和目标光图像D。图3(f)、(g)为大气光偏振度图像PA和目标光偏振度图像PD，图3(h)为重构后的目标图像J。通过实验结果可以看出，去雾后目标图像J中楼房、烟囱等目标变得清晰可见，图像边缘细节明显，且图像中没有出现明显的图像噪声。

图3 雾天重构实验结果Fig.3 Reconstruction experimental results under fog environments

图4为大气光偏振度图像PA和目标光偏振度图像PD的灰度直方图分布，不难发现，目标光偏振度图像灰度动态范围比大气光偏振度图像灰度动态范围宽，表明目标光和大气光同样具有偏振特性，都为部分偏振光，且大气光偏振信息和目标光偏振信息存在差异。

为了进一步验证本文方法在不同天气下的适用性，针对雾霾、雨、雪等不同天气开展了大量的实测实验。其中，图5是分别与Tan[5]、He[6]、Schechner[7-9]的重构效果比较。图5(a1)～(a3)为原始图像，其中，(a1)雾霾天PM2.5为200，能见度1 000 m；(a2)雨天降雨量20 mm/24 h，能见度800 m；(a3)雪天降雪量2.5 mm/24 h，能见度500 m。图5(b1)～(b3)为Tan的重构效果，图5(c1)～(c3)为He的重构效果，图5(d1)～(d3)为Schechner的重构效果，图5(e1)～(e3)是本文方法重构效果。实验结果表明本文方法能够从原始图像中较好地恢复出目标信息，并能有效降低重构后目标图像出现的图像细节丢失和噪声斑块，通过雾霾、雨、雪等不同天气下的实验说明本方法具有较好的环境适用性。

文中引入信息熵、平均梯度、灰度标准差和边缘强度4种统计特性参数作为定量评价标准。图5中各组实验图像的定量评价结果如表2所示。通过数据对比可知，本文方法整体上重构后图像的信息熵提升约40%，灰度标准差提升了约90%，平均梯度和边缘强度提高了3倍。数据表明本文方法在雾霾、雨天、雪天情况下均有较好的图像重构效果，且相对于以上3种重构方法，重构图像质量有所提升。

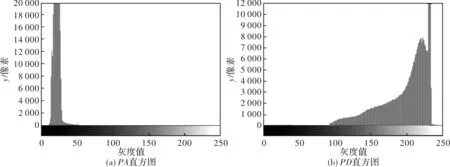
图4 PA和PD图像直方图Fig.4 PA & PD histograms

图5 重构实验对比Fig.5 Contrast of reconstruction experiments

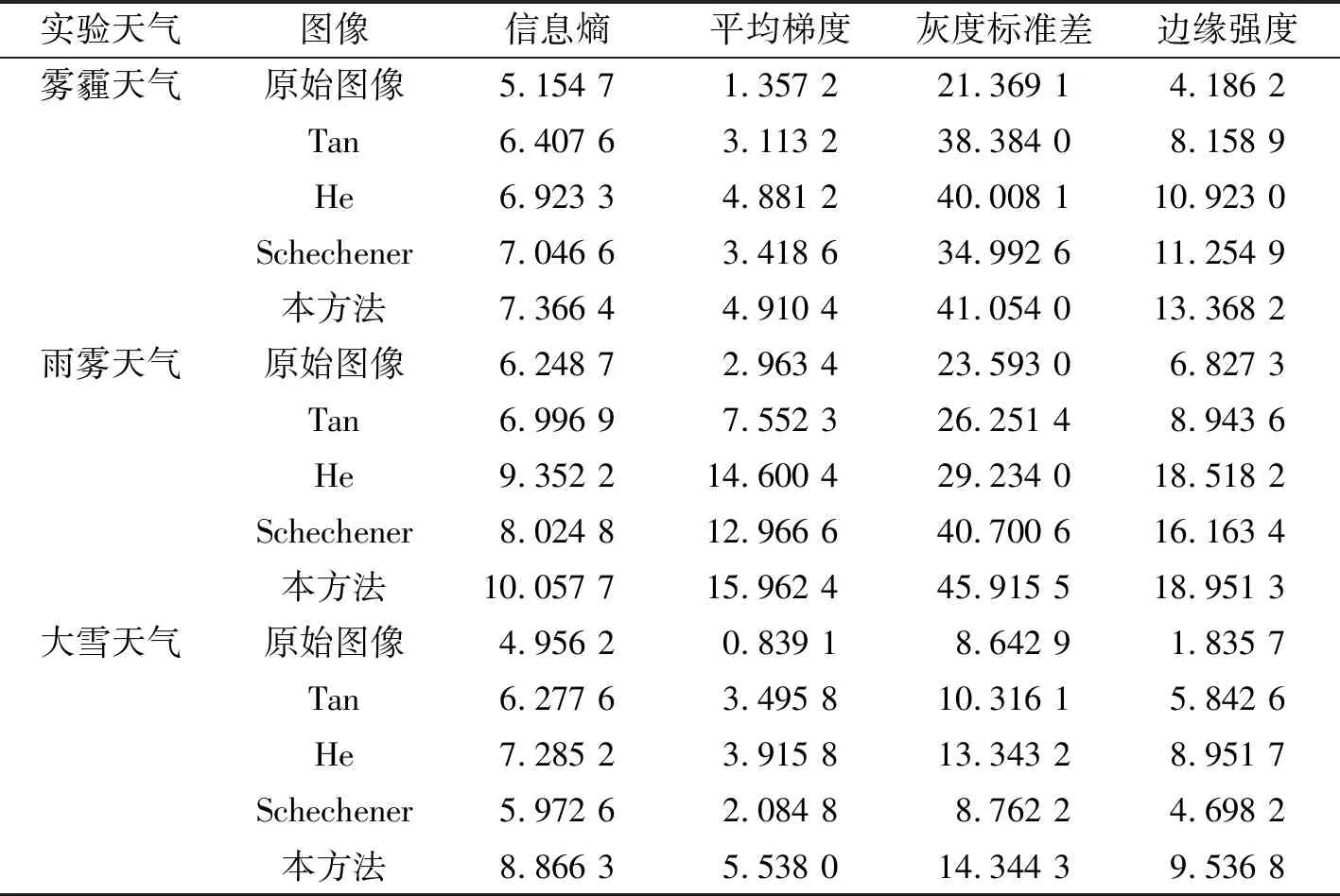
实验天气图像信息熵平均梯度灰度标准差边缘强度雾霾天气原始图像5.154 71.357 221.369 14.186 2Tan6.407 63.113 238.384 08.158 9He6.923 34.881 240.008 110.923 0Schechener7.046 63.418 634.992 611.254 9本方法7.366 44.910 441.054 013.368 2雨雾天气原始图像6.248 72.963 423.593 06.827 3Tan6.996 97.552 326.251 48.943 6He9.352 214.600 429.234 018.518 2Schechener8.024 812.966 640.700 616.163 4本方法10.057 715.962 445.915 518.951 3大雪天气原始图像4.956 20.839 18.642 91.835 7Tan6.277 63.495 810.316 15.842 6He7.285 23.915 813.343 28.951 7Schechener5.972 62.084 88.762 24.698 2本方法8.866 35.538 014.344 39.536 8

为了定量分析去雾后图像失真对比，采用结构相似度(SSIM)图像质量评价方法[16]，SSIM是一种常用的图像质量评价方法，来源于人类视觉系统能够高度自适应地提取场景中的结构信息，通过比较图像结构信息的改变而近似的反映图像失真，结构相似度值越大，图像失真度越小。

图6 无雾和有雾棋盘格图像Fig.6 Fogless and foggy checker board image

利用偏振光学模拟实验舱[17]模拟大气雾天环境，在偏振光学模拟实验舱内放置黑白棋盘格作为场景目标，用能见度仪测得的光透过率值表征烟雾浓度。首先采集一张无雾图像作为SSIM评价方法的无失真图像，其次在偏振光学模拟实验舱内模拟不同浓度的烟雾，获取不同浓度烟雾下的有雾图像。然后用以上4种去雾算法分别处理有雾图像，得到的目标图像作为待测试图像，利用SSIM方法分析比较目标图像的失真程度。

图6为室内实验获取的有雾和无雾棋盘格图像，其中图6(a)为无雾图像作为无失真图像，图6(b)～(f)分别为不同浓度的有雾图像。图7为目标图像的SSIM评价结果，SSIM指标越高，表明目标图像越接近于无失真图像。随着玻璃缸内烟雾浓度增加，去雾后目标图像质量降低，4种去雾方法的曲线均呈下降趋势。从整体上看，本文方法重构的目标图像SSIM指标一直高于0.6，能够较好的重构出目标图像，降低图像失真，且随着烟雾浓度的增加，本文方法的SSIM曲线下降最慢。

图7 结构相似性(SSIM)分析去雾图像质量Fig.7 Image quality analysis for defogging in structure similarity (SSIM)

4 结论

提出了一种利用目标和大气偏振信息的雾天图像重构方法。考虑目标光偏振信息和大气光偏振信息的差异性，首先，从光强图像中分离出目标光图像和大气光图像，并分别从目标光图像和大气光图像中解析目标光偏振信息和大气光偏振信息，构建偏振去雾模型；在高斯滤波中融合图像梯度信息代替常用的中值滤波方法，从偏振图像中，滤波估算出大气光强和目标光强，使滤波后的图像更平滑，保留了图像边缘细节；采用3σ法则阈值分割方法，滤除大气光图像中亮度异常的像素点，然后在大气光图像中估算无穷远处大气光强，避免了图像中噪声点和白色建筑物等高亮度目标的干扰；最后，重构出目标图像。在不同天气环境下开展外场实验，结果表明，该方法能够较好地在雾霾、雨、雪天气下重构出目标图像，并能有效降低图像细节丢失、图像噪声和图像失真，具有较好的环境适用性。