任意色散周期结构的时域有限差分方法分析

马立宪， 李燕茹， 陈 帅， 樊振宏

(1. 淮南师范学院 电子工程学院，安徽 淮南 232038；2. 南京理工大学 电磁仿真与射频感知工信部重点实验室, 江苏 南京 210094)

引言

近年来，复杂色散周期结构的应用获得较高的关注，例如应用在频率选择表面[1]、光子晶体[2]、太阳能电池上[3]。时域有限差分(finite-difference time-domain, FDTD)方法作为一种非常有效的电磁计算数值方法，已被广泛应用于求解这些色散周期结构的电磁波传播问题[4]。对于常见的色散媒质，根据色散媒质随频率变化的关系，在FDTD计算时，可等效为Debye、Drude、Lorentz及其混合色散模型[5]。国内外多位学者针对这些色散模型的FDTD算法进行了研究，先后提出了半解析递归卷积(PLRC)、辅助微分方程(ADE)、Z变换法等[6-8]。

采用上述算法在建模复杂色散媒质时需要高阶形式，这会导致FDTD计算时花费更大的内存空间和计算时间[9]。在处理多层色散媒质时，每种色散媒质得到的时域递推计算公式也不同，这给实际应用带来很大不便。本文提出将色散媒质模型的介电常数采用共轭复数对拟合的方式[10]，结合辅助微分方程法，给出了采用辅助微分方程法求解多层任意色散媒质的通用递推公式。对多层任意色散模型具有完全相同的形式，使用时只需给出介质模型的参数，不需再做任何附加推导，非常方便和灵活。根据Floquet定理[11]，文中分别求解了无限大周期结构Debye、Drude与太阳能电池模型的电磁波传播问题，数值计算结果与CST商用软件吻合，验证了本方法计算的有效性和普适性。

1 理论和数值推导

将色散媒质的介电参数ε采用共轭复数对的形式表示成任意色散模型的介电参数[10]，即：

(1)

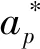
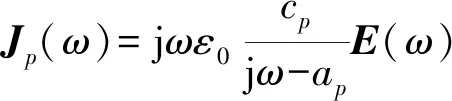
(2)

(3)

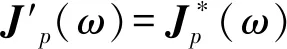
(4)

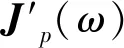
Δ×H(ω)=jωε0ε∞E(ω)+σE(ω)+

(5)

将(2)式利用傅里叶逆变换写成时域形式为

(6)

对(6)式再取中心差分近似以及平均值近似，得：

(7)

最终化简得Jp的计算表达式为

(8)

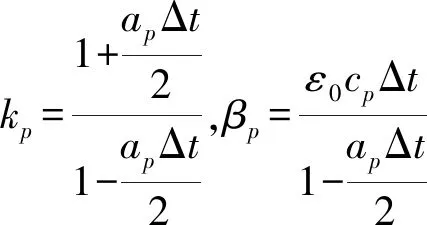
(9)

将(5)式转换为时域形式，得：

(10)

取中心差分近似及平均值近似得：

(11)

将(8)式代入(11)式，得到任意色散媒质模型的电场迭代公式：

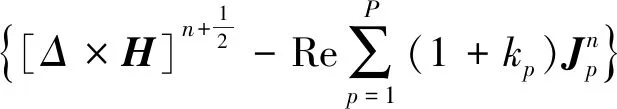
(12)

文中任意色散模型中的磁场的迭代公式保持不变[5]。

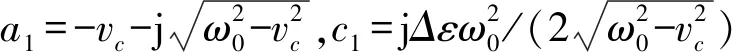
2 数值算例验证

2.1 Debye色散模型

如图1所示，周期结构的Debye色散模型厚度h=10 cm，以频率范围为30 MHz～120 MHz的电磁波垂直入射。该模型静态相对介电常数为εs=8.97，相对介电常数为ε∞=2.31，驰豫时间τ0=6.497×10-10s。利用上述Debye模型a1与c1计算表达式，可得到该模型介电常数的拟合公式，从而利用辅助微分方程法写出电磁场计算公式。在此取Yee网格在垂直方向的剖分尺寸为2 mm，在垂直入射时Debye模型的反射系数与透射系数的频带响应曲线如图2所示。从图2可以看出，计算结果与CST软件仿真很好地吻合。

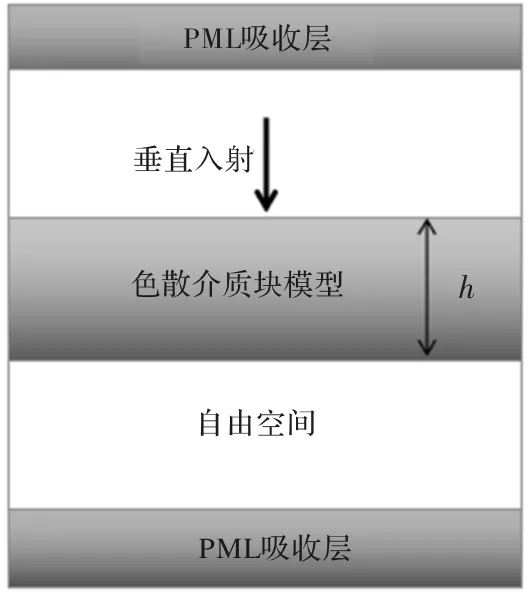
图1 色散介质模型示意图Fig.1 Schematic diagram of dispersive medium model

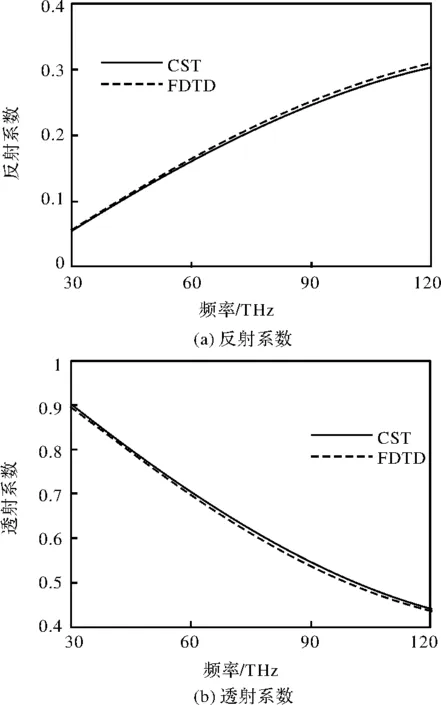
图2 Debye周期模型反射系数与透射系数Fig.2 Transmission coefficient of Debye periodic model

2.2 Drude色散模型

图1所示的Drude银板厚度h=20 nm，以频率250 THz～750 THz的电磁波垂直入射[14]。该色散模型相对介电常数为ε∞=1，碰撞频率vc=1.131×1014Hz，等离子体谐振频率ωp=1.332×1016rad/s，通过参数拟合程序拟合出计算所需复共轭级数对，如表1所示。

表1 Drude模型参数拟合表(ε∞=1)

Table 1 Parameter fitting table of Drude model

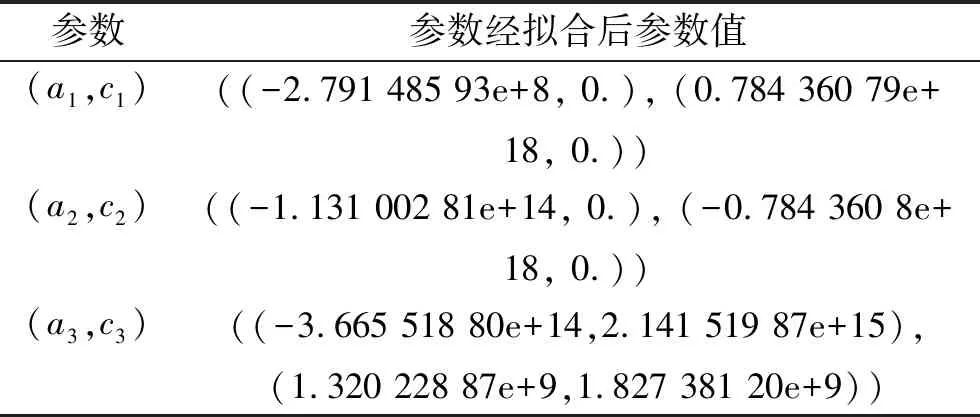
参数参数经拟合后参数值(a1,c1)((-2.791 485 93e+8, 0.), (0.784 360 79e+18, 0.))(a2,c2)((-1.131 002 81e+14, 0.), (-0.784 360 8e+18, 0.))(a3,c3)((-3.665 518 80e+14,2.141 519 87e+15),(1.320 228 87e+9,1.827 381 20e+9))

在本例中取Yee网格在垂直方向的剖分尺寸为0.5 nm，图3显示的结果是在垂直入射时Drude银板反射系数与透射系数的频带响应曲线。图3计算结果与CST商业软件较好地吻合，说明本文中的复共轭级数对参数拟合结合辅助微分方程FDTD方法能准确求解Drude色散媒质的电磁场传播问题。

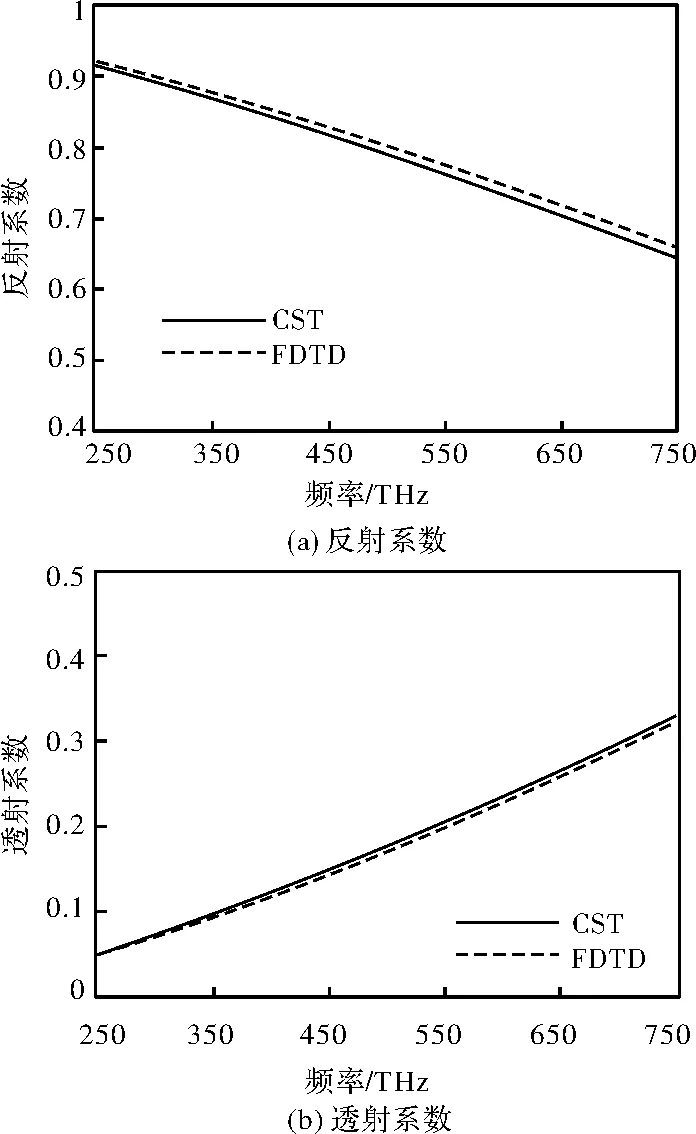
图3 Drude周期模型反射系数和透射系数Fig.3 Reflection coefficient and transmission coefficient of Drude periodic model

2.3 太阳能电池周期单元

太阳能电池周期结构单元尺寸如图4所示。x和y方向为周期边界，此算例中的太阳能活性层为P3HT和PCBM的聚合物，在其内部放置沿x轴均匀分布的正方体银离子，上部隔离层材料为PEDOT[15]。活性层、隔离层以及银离子的相对介电常数在可见光频段内(400 nm～800 nm)为色散媒质，并均可通过参数拟合方法拟合出相应的ap与cp。

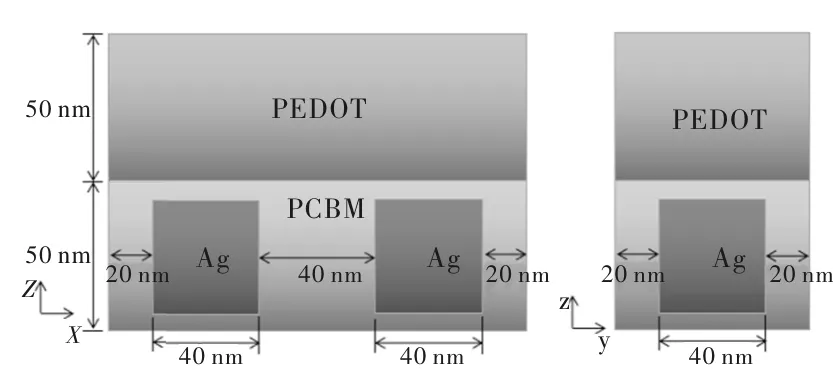
图4 太阳能电池单元示意图Fig.4 Schematic diagram of solar cell unit

在本例中，采用中心频率为562.5 THz的高斯平面波沿z轴方向负方向垂直入射，其电场极化方向为x轴正方向。采用辅助微分方程FDTD方法计算时，Yee网格在3个方向的剖分尺寸均为0.5 nm，计算得到的反射系数与透射系数频带响应曲线如图5所示。最后，我们把本例中3种材料的介电常数随频率变化的离散数值导入到CST商业软件中，通过CST软件自身拟合参数的功能实现如图5所示的反射系数与透射系数频带响应曲线仿真。通过对比发现，采用本文提出的方法得到的频带相应曲线与CST商用软件仿真得到的曲线十分吻合，进一步说明了本方法能较准确求解多层任意色散媒质的电磁波或光波传播问题。通过相关计算，继而可计算得到该太阳能电池模型的吸收系数，如图6所示。

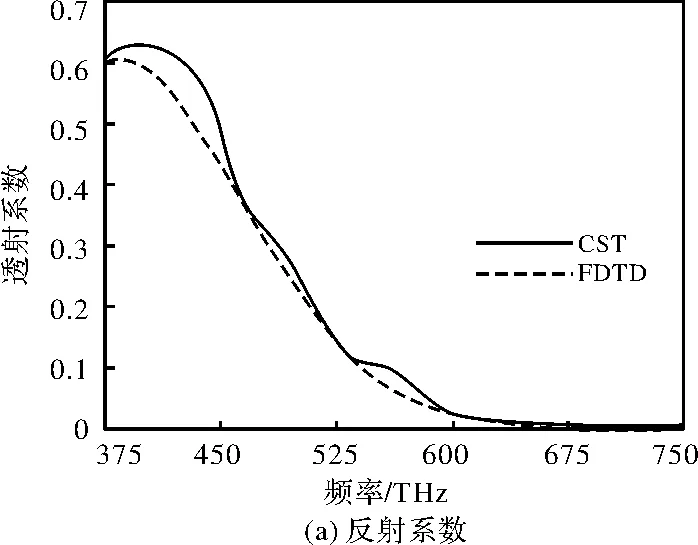
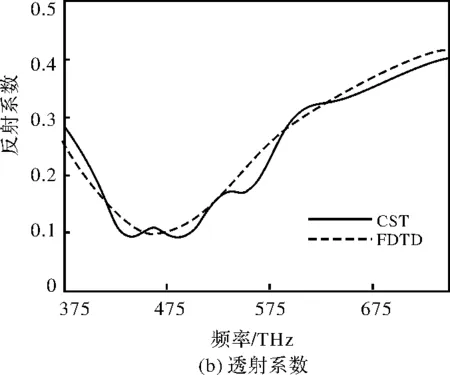
图5 太阳能电池单元反射系数和透射系数Fig.5 Reflection coefficient and transmission coefficient of solar cell unit

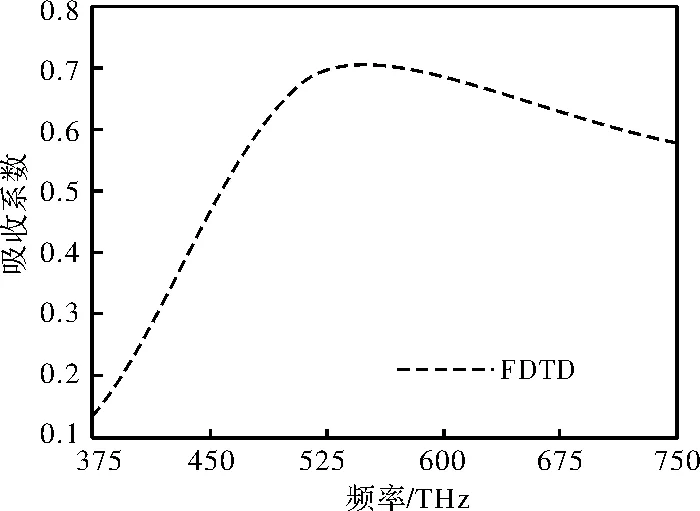
图6 太阳能电池单元吸收系数Fig.6 Absorption coefficient of solar cell unit

3 结论

通过上述算例说明,复共轭级数对拟合与辅助微分方程FDTD方法结合能较准确地分析任意色散媒质的电磁波传播特性。该方法针对多层任意色散媒质情况只需知道介电常数随频率变化的关系即可采用统一的迭代更新形式，保持了原有ADE-FDTD方法推导简单的优点，通用性强，为进一步求解太阳能电池的转换效率等提供了理论基础。考虑到在实际情况中，太阳能电池斜入射较为普通，后续将结合分裂场FDTD方法研究太阳能电池周期单元的斜入射问题。