五次长短波共振方程初值问题解的存在性
(上海理工大学 理学院,上海 200093)
1 问题的提出
Djordjevic等[1]在研究二维的毛细管重力波时,发现了描述长波和短波之间相互作用的演化方程

该方程还出现在内波、Rossby波及等离子体波等许多物理问题中[2]。
文献[3-4]分别用逆散射方法和先验估计方法证明了方程(1)初值问题整体解的存在性.文献[5]研究了方程(1)的n孤子解。
在文献[6]中,Benney建立了长波与短波相互作用的一般理论,提出了长波与短波相互作用的模型方程

式中: γ为常数;u是 复函数,表示长波;v是实函数,表示短波;|u|是u的模长。
文献[7]证明了方程(2)初值问题全局解的存在性。
1988年,Oikawa等[8]研究了双层流体中长波和短波在彼此分界面角度上的传播和共振作用,导出了(2+1)维长短波方程组,并将长短波方程拓展到高维空间,文献[9-14]分别研究了高维长短波方程及其推广形式解的存在唯一性。
还有学者研究了方程(2)在(1+1)维的推广形式,例如,文献[15]研究了广义LS型方程

的周期初值和初值问题。
2010年,Shang[16]研究了广义长短波方程

的孤波解和若干特殊形式的周期解。
定义泛函空间
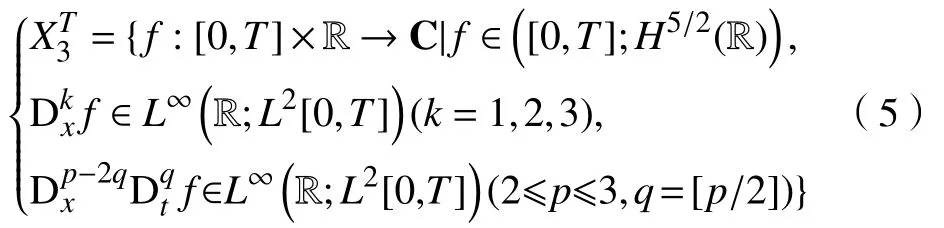
式中:Dx,Dt分别为关于x和t的偏微分。

方程(4)初值问题的初值条件为

本文的主要结果可以归结为定理1。


式中,所有的系数Cα均为正数。
统一将L∞(0,T;X)空间元素的范数记为。定义

式中:F ,F-1分别为傅里叶变换和逆傅里叶变换。
2 局部解的存在性
现利用压缩映射定理证明方程(4)在局部定义域上有解.




估计式(11)余下的项之前,先作出下面的估计。采用与式(15)和式(16)同样的估计方法,可得





3 全局解的存在性
首先证明方程(4)的解的守恒性质和2个先验估计结果,然后运用反证法,证明方程(4)初值问题的解在空间中的全局存在性。







致谢:在本文的研究过程中,得到了汪文军老师很大的帮助,在此表示衷心的感谢!

