无储光伏直供电设备收益快速评估方法

(1.国网上海市电力公司，上海 200122; 2.清华大学 电子工程与应用电子技术系，北京 100084)

随着光伏组件技术的进步，小容量的分布式光伏得到广泛应用。无储能、直供式的光伏电源被安装在路灯、通信基站的单元铁塔支架和数据机房屋顶等，与电网配合共同供给功率负载。通过控制光伏系统输出电压，使得光伏能源优先使用，达到节能减排的效果。文献[1]分析了采用光伏发电作为电力来源补充基站能源储备的可行性。文献[2]从经济性角度分析了“光伏铁塔”和光伏机房的收资状况，采用年利用小时数计算光伏发电收益。文献[3]提出了一套高效率的光伏供电系统，为通信基站提供可靠能源。文献[4]展示了在秘鲁圣克洛蒂尔德市搭建的17个通信铁塔光伏铁塔试验系统。文献[5]强调了光伏能源是解决节能减排问题的重要依托。文献[6-7]给出了在光伏集热器中估计光伏年收益的计算方法。文献[8]给出了多种估算发电和能耗的方式。

然而，上述文献均未详细分析光伏装机容量对于系统收益的影响。为达到最佳经济效益，需为负载配备合适的光伏设备容量，而根据年利用小时数的光伏收益估计方法仅适用于配备了储能或装机小于等于负载的光伏系统。当光伏装机大于负载时，由于系统未安装储能，可能出现由于光伏功率超出负载功率而弃光的现象，直接应用年利用小时数进行估算其发电收益将偏大。若直接利用一年365日光照曲线对发电收益进行仿真计算，则面临计算量大、数据难以获取等问题，不利于现场工程应用。

针对上述问题，本文提出了基于参数估计的无储光伏直供电设备收益快速评估方法，根据年利用小时数合理外推，建立了光伏发电收益关于光伏装机容量的负指数模型，并根据边界条件计算其模型参数。与采用NASA光照数据的精确仿真结果对比可得，利用本参数估计方法得到的收益-装机曲线与精确仿真曲线偏差较小，能够满足工程应用。

1 收益曲线负指数模型

1.1 年利用小时数估计方法

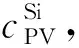
(1)

设负载功率为PL，市电价格恒定为cG，本地光伏年利用小时数为TPV，则当光伏装机小于等于负载功率即满足PPV≤PL时，光伏年收益IPV可近似由下式计算

IPV=PPVTPVcG,PPV≤PL

(2)

1.2 负指数模型

当光伏装机大于负载功率时，可能出现光伏瞬时可出力功率大于负载功率的情况。为保证功率平衡，光伏控制器将超出部分功率旁路消耗，导致一定程度的弃光。此时，若直接根据利用小时数估算光伏系统年收益，会得出偏大的结果。

考虑到光伏收益存在明确的上确界，即只要有光照就全部由光伏系统向负载供电，此时光伏年收益为

(3)

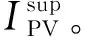
IPV=a1ea2pPV+a3,PPV>PL

(4)

其中a1<0、a2<0、a3>0为待估计参数。考虑到收益函数整体的连续性、光滑性和上确界，有

IPV(PL)=a1ea2PL+a3=PLTPVcG

(5)

(6)

IPV()=a3=PLTsuncG

(7)

根据(5)～(7)可解出参数a1、a2、a3为

a3=PLTsuncG

(8)

(9)

(10)

则式(2)、(4)共同描述了光伏收益与光伏装机之间的关系。

2 最佳收益点计算

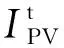
(11)

画图得知，其有唯一最大值(极大值)点，在PPV>PL取到，计算式(11)的导数为

(12)

得其极值点为

(13)

实际工程中，可根据项目规划年，根据式(13)求得该条件下最佳光伏装机容量。

3 算例分析

本文采用了南京、哈尔滨、丽江、潍坊、驻马店和格尔木这六个城市的数据进行算例分析。设定光伏板按照最佳安装角安装且无遮拦。这六个城市的年利用小时数和最佳安装倾角如表1所示。另一方面，根据NASA网站[9]获取其卫星采集到的上述六地辐射数据，参考文献[10]中的计算公式(详见附录1)，绘制单位功率光伏年出力曲线(8 760 h)，并结合负载功率进行仿真计算。以哈尔滨为例，图1给出了根据NASA数据计算的1 kW光伏板年出力曲线。表2给出了本算例用到的成本数据。

表1光伏年利用小时数数据表

城市南京哈尔滨丽江潍坊驻马店格尔木小时数/h1 069.81 239.91 493.71 412.91 251.41 695.5安装角/°234029352838

表2光伏成本数据

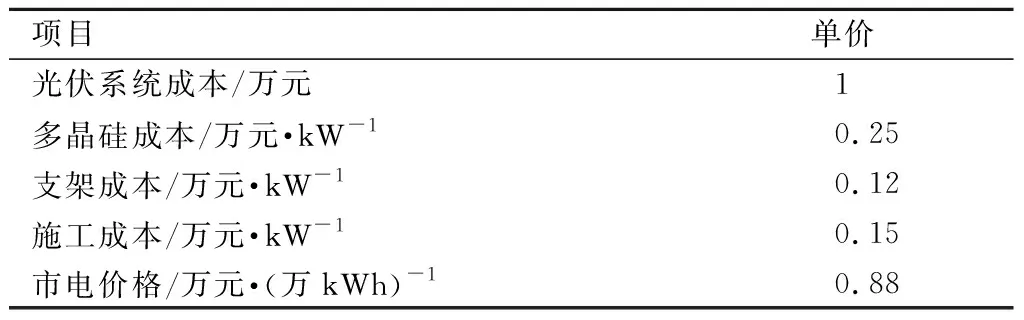
项目单价光伏系统成本/万元1多晶硅成本/万元·kW-10.25支架成本/万元·kW-10.12施工成本/万元·kW-10.15市电价格/万元·(万kWh)-10.88

3.1 定负载收益曲线对比

设负载为PL=3 kW，比较上述六城市按照本文所提负指数模型与NASA数据精确仿真进行收益评估所得结果。作出年收益驻马店与光伏装机之间的关系曲线如图2所示。图中实线为采用本文负指数模型绘出的收益估计曲线，虚线为采用NASA数据仿真得到的收益曲线。可以看出，在光伏装机小于负载功率时，两线几乎重叠，表明此时根据利用小时数可准确估计光伏年收益。当光伏装机大于负载功率时，南京、哈尔滨、潍坊和驻马店的参数估计模型仍能较好的拟合仿真结果，而丽江、格尔木这两个利用小时数较大地区的结果则略有偏差。其中，在光伏装机大于负载两倍功率时，本文所提负指数模型相对于仿真结果所计算收益较小、偏保守。总体而言，本文的参数模型能够较为精确地刻画当光伏装机大于负载功率时的年收益变化趋势。

3.2 最佳收益点估算

由式(13)可以看出，最佳光伏装机容量同设备预期工作年限t有关。作出在负载PL=3 kW上述六个城市最佳光伏装机容量同预期工作年限t之间的关系曲线如图3所示。

可以看出，随着设定工作年限的上升，最佳光伏装机容量呈上升趋势，且利用小时数越大的地区其上升速率越慢。最佳光伏装机普遍高于负载功率，且在工作年限为10年时，不同地区的最佳光伏装机均接近8 kW。这说明，当设定工作年限为10年时，存在一个不同地区普适的最佳光伏装机。

3.3 不同负载水平下最优装机及收资相抵年

本文进一步探究了负载功率对于最佳光伏装机容量的影响。在此算例中，我们采用了哈尔滨的参数数据，针对不同的负载功率，通过改变光伏装机计算其最短的收资相抵年，并将此时的光伏装机记为最短收资相抵年时的最优装机，如图4所示。

可以看出，随着负载功率的上升，最优光伏装机基本呈线性增长趋势，而最短收资相抵年呈负对数下降趋势。这说明随着负载功率的增加，在合理配置光伏装机时可以在更短时间内收回成本。

4 结论

本文提出了基于参数估计的无储光伏直供电设备收益快速评估方法，根据年利用小时数合理外推，建立了光伏发电收益关于光伏装机容量的负指数模型，并根据边界条件计算其模型参数，其结果与采用NASA光照数据的仿真结果偏差很小。进一步利用该模型计算了不同工作年限设置和不同负载下的最佳光伏装机容量，为指导工程报装提供了便捷、有效的计算手段。未来的工作将继续探索含储能光伏系统中储能和光伏的最佳联合配置问题。

附录：NASA辐射计算公式

根据以下公式[10]和NASA网站数据可计算给定倾角斜面上的辐射强度Hth

Hh=rtH

(14)

Hdh=rdHd

(15)

(16)

(17)

A=0.409+0.5016sin[ωs-(π/3)]

(18)

B=0.660 9-0.476 7sin[ωs-(π/3)]

(19)

δ=23.45*sin[6.303*(284+n)/365]

(20)

cosθzh=cosφcosδcosω+sinφsinδ

(21)

cosθh=cosθzhcosβh+sinθzhsinβhcos(γsh-γh)

(22)

γsh=sin-1(sinωcosδ/sinθzh)

(23)

(24)

式中H——水平表面上的辐照度;

Hd——水平表面上的月平均漫射辐射;

ω——太阳时角;

ωs——日落小时角;

φ——纬度;

n——一年中的天数标号;

βh——光伏阵列相对于水平表面的倾角;

γh——倾斜表面的表面方位角;

θzh——太阳相对于水平面的天顶角;

θh——太阳天顶角相对于倾斜的太阳能电池板的法线的夹角。