云计算平台上的Canopy-Kmeans并行聚类算法研究

孙秀娟

摘  要： 针对大数据的高维特性及海量性，提出云计算平台中的Canopy?Kmeans并行聚类算法，通过三角不等式原理，能够使计算冗余降低，使算法执行速度得到提高。对Canopy?Kmeans并行聚类算法进行深入的研究，并且在大量不同大小数据集中的实验结果表明，所设计的并行聚类算法具有良好的加速比、数据伸缩率及扩展率等特点，能够在海量数据挖掘及分析中使用。

关键词： 云计算平台; Canopy?Kmeans算法; 并行聚类算法; 大数据挖掘; 集群数据; 数据分析

中图分类号： TN911.1?34                       文献标识码： A                          文章编号： 1004?373X（2019）19?0078?04

Abstract： The Canopy?Kmeans parallel clustering algorithm in cloud computing platform is proposed for the high?dimensional feature and massive nature of big dat. The computational redundancy of the algorithm can be reduced and its execution speed can be improved according to the principle of triangular inequality. Canopy?Kmeans parallel clustering algorithm is studied in depth. The results from experiments of a large number of data sets show that the designed parallel clustering algorithm has the characteristics of high acceleration ratio， and data scalability and expansion rate， and can be used in massive data mining and analysis.

Keywords： cloud computing platform; Canopy?Kmeans algorithm; parallel clustering algorithm; big data mining; clustering data; data analysis

0  引  言

目前，在大数据处理过程中大部分都是使用分布式或者并行架构，使系统扩展性得到提高，并且通过多线程并行式结构、基于Apache的开源云计算Hadoop平台进行实现，其中，使用最为广泛的就是K?means算法。相关研究人员提出将MPI作为基础的分布式聚类，其虽然能够通过集中式存储，使算法时效性得到提高，但是此算法在进行计算的过程中为单节点运行，在大数据处理聚类分析任务过程中的算法效率并不快[1]。所以，又提出Canopy?Kmeans改进算法，对于传统算法的问题，使用最小最大的原则，通过云计算平台集群计算及存储能力，使此算法的有效性及时效性得到提高。本文基于K?means算法，使用三角不等式原理，提出Canopy?Kmeans并行聚类算法[2]。通过开源云计算平台及分布式框架，结合三角不等式定理，并且在大数据预处理过程中实现原始大数据预处理，实现算法的改进。

1  算法实现

在实现数据挖掘的过程中，主要特点就是从海量数据中将有价值的信息及时提取出来。在网络时代到来之后，现代数据种类及数据量也都在不断的提高，传统数据挖掘技术已经无法使数据挖掘需求得到满足。在云计算时代中，海量数据在不同计算机中分布，目前聚类算法在时间及空间复杂性方面都无法使此问题得到解决。那么本文的主要研究思路就是在目前聚类算法中使用并行处理技术，使聚类算法时间及空间的复杂度得到降低，以此使聚类时间得到缩短。

1.1  编程的思想

MapReduce属于海量数据处理的并行编程模式及计算框架，其在大规模数据集并行计算中使用。简单来说，MapReduce为任务分解及结果汇总[3]。首先，就要得到聚类数据[N]个样本对象，将其定义为：[N]指的是样本总数量，也就是每个样本都是通过[m]个属性共同特征所构成。初始数据以数据存储节点和Mapper个数量划分成为相应数据集数量，能够为Mapper节点分配数据集实现独立执行，之后利用相应的Reducer处理结果，并且对下一轮迭代进行判断[4]。

1.2  基于距离三角不等式的聚类算法

在云计算平台中的MapReduce框架中，通过传统K?means算法和距离三角不等式定理相互结合，从而提出基于距离三角不等式聚类算法。此算法使用三角不等式定理，任何一个三角形的两边之和都比第三边要大，两边之差要比第三边小。使其扩充到欧几里得空间，因为欧氏距离能够使三角不等式原理得到满足，从而能够降低聚类算法计算过程中的复杂度，使大数据聚类分析效率得到提高。

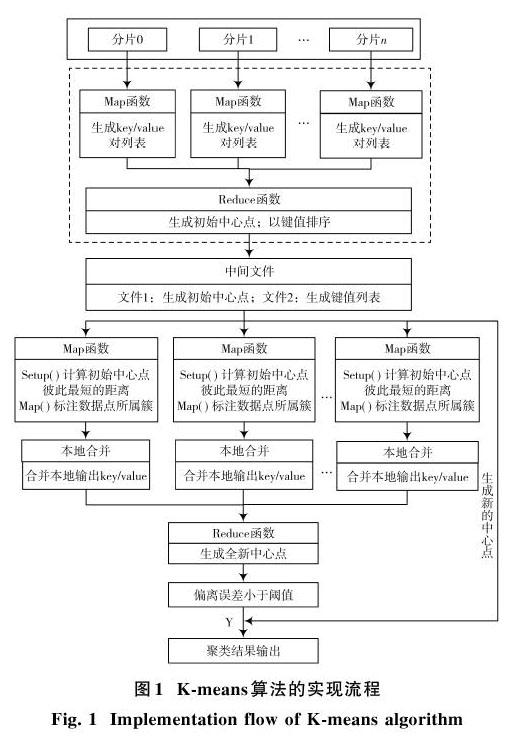
假设在欧几里得空间中有[X]，[C1]，[C2]三個任意数据点，数据点之间的距离能够满足三角不等式原理：[d（X，C1）+d（C1，C2）≥d（X，C2）]，[d（C1，C2）-d（X，C1）≤][d（X，C2）]。如果[X]指的是数据空间中的任何数据点，[C1]和[C2]都是两个簇中心点。假如[2d（X，C1）≤d（C1，C2）]，并且在两边减去[d（X，C1）]，那么就有[2d（X，C1）-d（X，C1）≤d（C1，C2）-d（X，C1）]。所以，假如[2d（X，C1）≤][d（C1，C2）]，那么则有[d（X，C1）

由上述原理可知，K?means的算法思想就是通过预处理之后的初始中心点对不同中心点彼此最短距离进行计算，之后以三角不等式原理对集合中的数据点到第一个数据中心点距离进行计算。假如数据点到中心点的距离的两倍小于或者等于第一个数据中心点到其他数据中心点的最短距离，那么此数据点就为第一个数据中心点，将其标记为第一类。以此类推，实现全部数据点标记。

1.3  Map函数的设计

Map函数输入指的是MapReduce框架默认的格式，也就是key指的是目前样本相对输入数据文件起始点偏移量，ualue指的是目前样本各维坐标值构成字符串。首先，通过ualue实现目前样本各维值的解析;然后，对其和[k]个中心点距离进行计算，寻找距离最近聚簇下标;最后，实现的输出，key1指的是距离最近聚簇下标，ualue1指的是目前样本各维坐标所构成的字符串[5]。

为了能够降低算法在迭代过程中传输数据量及通信代价，在操作Map以后，PKMeans算法中实现Combine操作的设计，使每个Map函数处理之后输出数据实现本地合并。由于每个Map操作之后输出函数都是在本地节点中存储，所以所有Combine操作都是通过本地进行执行，通信代价比较小[6]。

1.4  Combine函数的设计

Combine函数在对对输入的过程中，key属于聚簇下标，[V]指的是为下标分类的聚簇所有样本各维坐标值构成的字符串链表。首先，基于字符串链表实现所有样本各维坐标值的依次解析，并且使全部相应坐标值都相加，记录下链表样本的总数量。输出中的key1指的是聚簇下标，ualue1指的是字符串，其中主要包括各维的坐标值及样本总数量和、构成字符串等信息[7]。

1.5  K?means算法的设计

K?means算法的执行过程为：

1） 使数据集上传到HDFS中，实现数据分片，并且使所有分片都在DataNodes中存储，实现初始中心点集合[U]的输出，将其作为全局变量;

2） 在所有计算节点中，对每个中心点到其他中心点最短距离[D]集合进行计算[8];

3） 以距离三角不等式的原理，使满足条件需求数据点到中心点簇进行划分，并且将数据集[V]中已经划分的数据点删除。假如数据集[V]中存在不满足条件的数据点，以计算过程中的数据点到不同中心点距离对相应簇进行分配，并且将数据集[V]中的相应数据点进行删除;

4） 实现全新中心点的生成;

5） 返回到步骤2）对数据中心点重新进行计算，直到数据中心点没有变化，结束算法;

6） 对子节点进行规约，实现聚类结果的输出。

K?means算法的实现流程如图1所示。

Setup函数：

输入：初始簇中心点集合表示为[U={C，C1}]，[K]值;

1. 对全部中心点[C]与[C1]实现[d（C，C1）]的计算;对全部中心点[C]，[S（C）=]min[（d（C，C1））（C≠C1）];

2. 对全部中心点[C]与[C1]进行计算，得到彼此最短距离，并且在相应数组中进行保存;

3. 假如中心点出现变化，那么重复以上步骤。

Map函数：

输入：实现簇中心集合[U]的输入，并且实现数据集[V（v1，v2，…，vn）]的输入;

输出：[K]中心点的集合[U]。

1. [U=U];

2. while（true）

3. 对[V]中数据点到中心点[C]距离[d1]进行计算;

4. If（[2d1≤S]），其中数据点的标记为第一个中心点簇，同时从[V]中将此数据点删除，并且将不符合条件的数据点到此中心点的距离保存到数组[D]中。以此类推，直到对[V]中全部聚类进行计算，并且对簇进行标记;

5.  If（[V！=]Null），以上个中心点距离[D]，对[C]最短距离进行计算，选择距离中心点最近的簇实现标记，并且从[V]中将此数据点进行删除;

6. 对已经标记点簇全新的[C]进行计算;

7. 对上一个中心与最新中心点之间的距离进行计算;

8.  If（Distance==0）;

Break

Else;

9. 返回到步骤3）重新计算;

10. End while

为了使大数据在主节点和子节点通信时间得到缩短，此算法在MAP函数以后实现Combine操作的设计，其主要功能就是合并本地节点数据文件，降低大数据I/O传输。图2为MAP并行化的过程。

2  实  验

2.1  實验平台

云计算的平台结构如图3所示，在进行实验的过程中，将一台机器作为数据JobTracker及NameNode服务节点，另外的三台为TaskTracker及DataNode服务节点，每台计算机都能够对4个MAP数据任务进行处理。

2.2  单机处理实验对比

信息数据处理的实验内容比较集中，都是在某个群数据节点中，和串行聚类K?means算法处理相同规模数据中消耗的时间如表1所示。[T1]的设置数值指的是串行算法计算，[T2]数值指的是通过MAP模型实现的计算时间。

通过表1可知，在目前小数据中，串行算法效率要比MAP模型中的计算效率高。出现此种结果的主要原因就是基于MAP计算模型中，聚类K?means算法在每次迭代计算过程中都要重新进行设置，以此能够形成全新的工作任务，但是在完成工作的过程中要消耗一定计算资源。在计算机数据信息量规模达到一定程度时，单机处理算法就会使计算机在计算的过程中出现内存不足的情况。以此表示，Map模型的可靠性比较强，充分展现了云计算平台数据处理能力。

2.3  集群数据的计算实验

在本次实验内容中，如果增加目前计算机硬件资源，计算机系统中的计算数据规模相同，表2为实验数据。通过表2可以看出，每条计算得到的数据都是通过四维状态下数值类型组合构成，计算模型的计算程序也通过既定标准生成5种计算类型。对比规模大小完全相同的计算数据，在计算过程中如果出现增加节点的情况，系统完成计算任务所消耗时间会减少，以此实现计算大规模数据实效性。由此可知，在大规模数据计算的过程中，利用节点的增加能够提高系统的计算成效。

3  结  语

总之，目前网络技术在不断的发展，尤其是云计算技术和网络技术的广泛使用，海量数据处理的过程也越来越复杂，以此对于空间及时间复杂度的需求也在不断的提高。那么，就要利用数据处理模式，使聚类时间及对于海量数据延展能力降低。本文所设计的并行聚类算法通过实验表明其能够满足实际需求。

参考文献

[1] 孟海东，任敬佩.基于云计算平台的聚类算法[J].计算机工程与设计，2015，11（11）：2990?2994.

MENG Haidong， REN Jingpei. Clustering algorithms based on cloud computing platform [J]. Computer engineering and design， 2015， 11（11）： 2990?2994.

[2] 霍可栋.基于Hadoop平台下的Canopy?Kmeans算法实现[J].科技展望，2015，25（33）：87?88.

HUO Kedong. Implementation of Canopy?Kmeans algorithm based on Hadoop platform [J]. Prospects for science and technology， 2015， 25（33）： 87?88.

[3] 牛怡晗，海沫.Hadoop平台下Mahout聚类算法的比较研究[J].计算机科学，2015，42（z1）：465?469.

NIU Yihan， HAI Mo. Comparison research on Mahout cluste?ring algorithms under Hadoop platform [J]. Computer science， 2015， 42（S1）：  465?469.

[4] 崔莉霞.基于Hadoop的并行聚类算法的研究[J].计算机光盘软件与应，2014，12（23）：141?142.

CUI Lixia. Research on parallel clustering algorithm based on Hadoop [J]. Computer CD software and application， 2014， 12 （23）： 141?142.

[5] 高见文，薛行贵，罗杰，等.基于迭代式MapReducede的海量数据并行聚类算法研究[J].中国科技论文，2016，11（14）：1626?1631.

GAO Jianwen， XUE Xinggui， LUO Jie， et al. Research on parallel clustering algorithm for massive data based on iterative MapReducede [J]. Chinese science and technology paper， 2016， 11（14）： 1626?1631.

[6] 李琪，张欣，张平康，等.基于密度峰值优化的Canopy?Kmeans并行算法[J].通信技术，2018，51（2）：85?86.

LI Qi， ZHANG Xin， ZHANG Pingkang， et al. Canopy?Kmeans parallel algorithm based on density peak optimization [J]. Communication technology， 2018， 51（2）： 85?86.

[7] 肖雪平，倪建成，曹博.基于Map?Reduce模型的BCkmeans并行聚类算法[J].电子技术，2016，11（5）：78?79.

XIAO Xueping， NI Jiancheng， CAO Bo. BCkmeans parallel clustering algorithm based on Map?Reduce model [J]. Electronic technology， 2016， 11（5）： 78?79.

[8] 张友海，李锋刚.基于MapReduce的Canopy?Kmeans算法的并行化[J].辽宁科技学院学报，2017，19（1）：4?5.

ZHANG Youhai， LI Fenggang. Parallelization of Canopy?Kmeans algorithm based on MapReduce [J]. Journal of Liaoning University of Science and Technology， 2017， 19（1）： 4?5.