基于颗粒流的高填黄土明洞加筋减载数值模拟分析

姚玉相， 李 盛, *， 马 莉， 王 焕， 王长丹

(1. 兰州交通大学 道桥工程灾害防治技术国家地方联合工程实验室， 甘肃 兰州 730070；2. 兰州工业学院土木工程学院， 甘肃 兰州 730050； 3. 中铁十四局集团有限公司， 山东 济南 250014；4. 同济大学 道路与交通工程教育部重点实验室， 上海 201804)

0 引言

高填方明洞在山区高等级公路的修建中应用十分广泛。然而，高填方明洞洞顶上覆土荷载往往较大，再加上明洞与回填土之间较大的刚度差异，会导致洞顶纵向开裂从而引发工程事故。为减小高填方明洞洞顶的受力，保证明洞衬砌结构的安全性和稳定性，需对高填方黄土明洞洞顶土压力的减载措施及相应减载规律进行深入研究。

国内外研究者在填方结构物减载措施方面进行了大量研究，并取得了一定的成果。Dancygier等[1]、Larsen等[2]在管涵上铺设干草进行土压力减载试验，得出铺设干草对于防止管涵开裂有积极的作用。顾安全等[3-4]、白冰[5]利用EPS板对涵顶土压力减载进行了多项室内试验，证明了在涵顶铺设EPS板(expanded polystyrene board)可以起到很好的减载效果，同时推导了该减载条件下涵顶土压力的计算公式。Sun等[6]在涵顶铺设EPS板进行减载，并运用FLAC4.0软件研究了涵顶、涵底、涵侧土压力的变化规律。郑俊杰等[7]结合室内和现场试验，研究了涵洞的土工格栅加筋减载，推导了加筋减载结构涵顶土压力的计算公式。李盛等[8]研究了不同减载方案下高填方明洞土压力随填土高度变化的规律以及土拱效应，提出了仅铺设土工格栅减载的明洞洞顶土压力计算公式，并将其成功运用到了实际工程中。文献[9]通过考虑边坡坡角、沟槽宽度、明洞高宽比等因素，建立了高填明洞的土压力计算模型，推导了明洞洞顶土压力的计算公式。文献[10]推导了高填方黄土明洞洞顶铺设EPS板和土工格栅共同减载的明洞洞顶土压力计算公式，并利用ANSYS软件进行模拟分析，将模拟结果与公式计算结果进行对比，验证了公式的正确性。文献[11]采用有限元数值模拟方法，研究了有、无EPS板减载时高填黄土明洞不同位置处衬砌结构内力和厚度随回填土高度的变化规律。

另外，关于土拱效应的离散元研究也有不少。Terzaghi[12]1943年最早利用活动门实验证实了土拱效应的存在。周兴涛等[13]采用细观颗粒流软件PFC2D对沟埋涵洞上方填土内土拱效应及涵顶垂直土压力进行了研究，结果表明涵洞上方填土越高，土拱效应越明显，沟槽越宽，土拱效应越弱。向先超等[14]利用细观颗粒流方法，研究了影响抗滑桩土拱效应的因素，揭示了这些因素对土拱的极限承载能力、残余承载能力和桩土荷载分担比的影响规律。许朝阳等[15]采用二维颗粒流程序PFC2D建立了基于模型试验的细观数值分析模型，对桩承式路堤中土拱效应的荷载传递机制进行了研究。郭红梅[16]参照前人室内模型试验，采用颗粒流软件PFC2D建立离散元(DEM，discrete element method)数值模型，对桩承式路堤中的接触力分布、主应力偏转、竖向位移和侧向位移等进行了深入分析。韩高孝等[17]利用颗粒流离散单元计算软件模拟太沙基活动门实验，对摩擦型岩土材料土拱效应的影响因素进行了深入研究，得出了随着活动门的下移土拱效应在不断调整的结论。

国内外学者对于土压力减载的研究，大多都是基于连续介质理论或是对土体宏观参数进行分析，忽略了土体本身的离散特性，而采用离散元方法的研究也主要是针对涵洞和桩承式路堤的土拱效应，对于高填黄土明洞加筋减载的细观研究鲜有报道。因此，本文利用基于离散元理论的颗粒流软件PFC2D，从散粒体和微观角度分析了土工格栅加筋减载明洞荷载传递机制，得出了加筋减载明洞洞顶土压力变化的一般规律，并进一步研究了土工格栅刚度和层数对洞顶减载效果的影响。

1 颗粒流数值模拟

本文数值模拟采用Lai等[18]提出的IMCM(improved multi-layer compaction method，即改进的多层压实方法)生成初始模型。该方法能够有效减小生成初始模型时的水平应力，使地应力沿深度呈梯度场分布。同时，为研究不同减载措施对高填黄土明洞洞顶土压力的减载效果，共建立了4种计算模型，具体计算方案见表1。

表1 模拟计算方案

1.1 模型建立及测点布置

本文参照文献[8]的室内模型试验，按照几何相似常数为1/30建立高填黄土明洞减载的颗粒流模型，模拟现场最大填土高度30 m的黄土明洞。鉴于上述各计算工况的建模过程相似，本文仅对工况YYX4的建模过程进行详细描述，相应的数值模型图如图1所示。

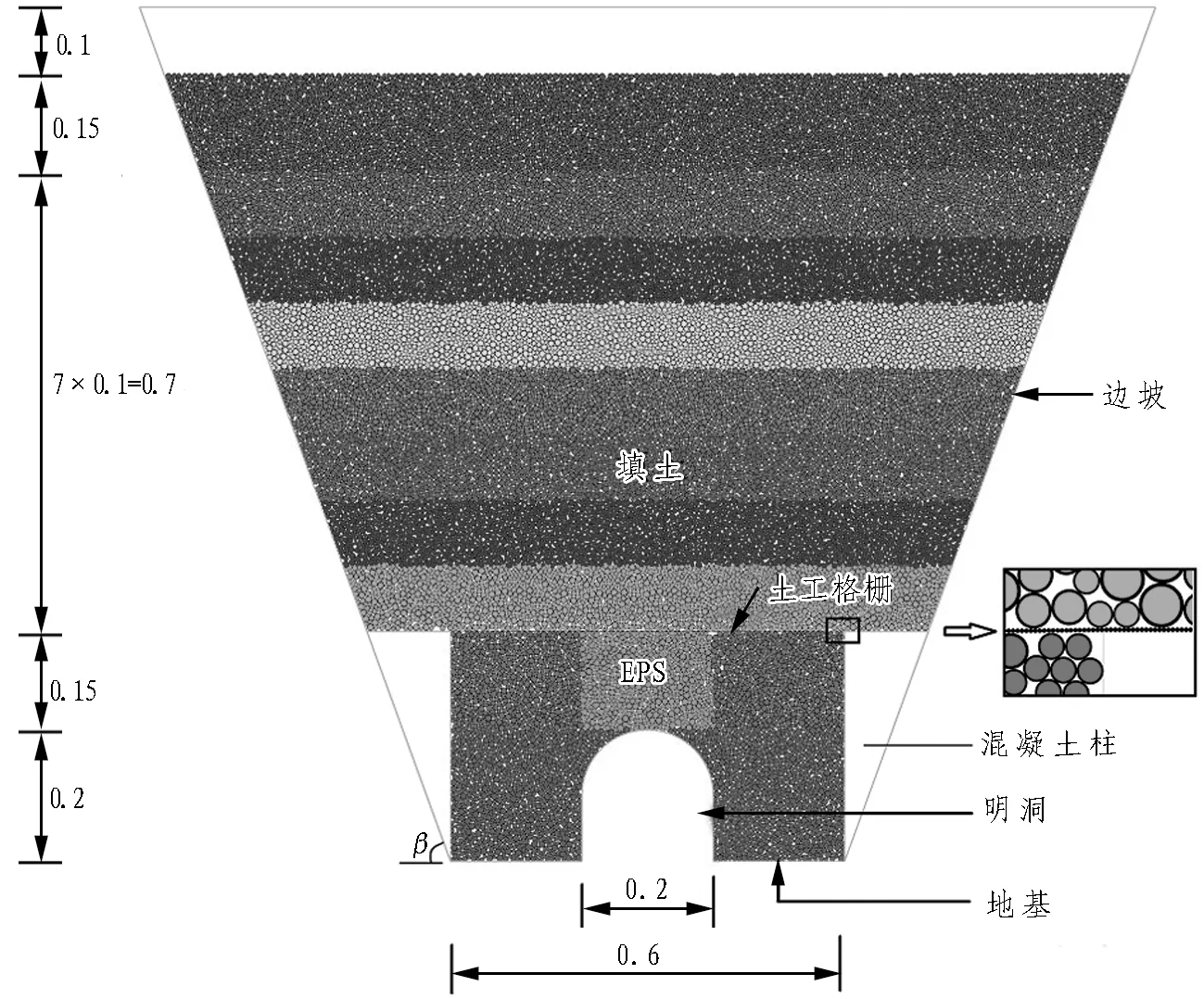
图1高填黄土明洞减载离散元模型(单位： m)

Fig. 1 DEM model of load reduction for high-filled open-cut tunnel (unit: m)

整个模型槽的高度为1.3 m，其中，明洞高度为0.2 m，EPS板的厚度为0.15 m，拱顶以上回填土高度为0.85 m，预留空白区域的高度为0.1 m；模型箱底部沟槽宽0.6 m，明洞宽0.2 m。混凝土柱位于明洞两侧边坡处，并与边坡连为一个整体，其高度为沟槽底部至EPS板顶的距离，详细位置如图1所示。边坡、明洞、地基和混凝土柱均采用wall模拟，填土、EPS板和土工格栅均采用圆盘颗粒模拟。填土采用IMCM法分层填筑在坡脚β为70°的模型槽内。生成EPS板时，先在放置EPS板的位置处生成一个矩形墙(长0.2 m×高0.15 m)，同时删除该矩形墙内的颗粒，然后利用PFC2D自带的半径扩大法程序[19]生成颗粒集合。生成土工格栅时，先在放置土工格栅的位置处生成上下平行且间距为1 mm的2个引导墙，随后删除墙内的颗粒，最后在该引导墙内生成粒径为1 mm且相互黏结的颗粒，土工格栅一直延伸至边坡，详见图1中的局部放大图。此时，由于矩形墙和引导墙的介入，破坏了模型之前的平衡状态，故需要将模型运行足够多的步数以消除颗粒间的不平衡力，进而获得初始平衡状态。模型达到初始平衡状态后，再删除矩形墙和引导墙，然后赋予模型合适的细观参数，并在重力的作用下达到最终平衡状态[18, 20]。

此外，模型中布置了一定数量的测量圆和位移测量点，用于测量模拟中各位置的应力、孔隙率和竖向位移。其中，编号①—的测量圆用于测量洞顶竖向土压力，编号④—⑧的测量圆同时用于测量洞顶平均竖向土压力，编号⑤—⑦的测量圆同时用于测量洞顶上方土体中的孔隙率，编号—的测量圆用于测量混凝土上的竖向应力，编号—的测量圆用于测量混凝土柱之间土体的竖向应力，测量圆⑥和测量圆—用于测量模型中不同深度位置处的竖向应力。测点位置示意图见图2。图2中虚线表示填土顶面。

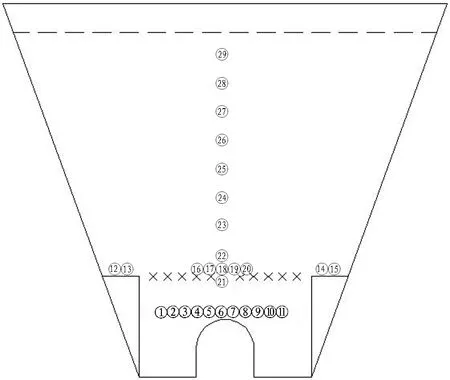
〇—测量圆; ×—位移测量点。

图2测点位置示意图

Fig. 2 Schematic diagram of measuring point position

1.2 材料细观参数确定

填土材料选用相对压实度为80%、压缩模量为2.67 MPa、孔隙率为0.2、黏聚力c=20 kPa、内摩擦角φ= 24.6°的黄土[21]。表征黄土宏观特性的基本力学参数有黏聚力和内摩擦角。为了模拟黄土颗粒间的黏结作用，填土颗粒间的接触本构模型选择线性接触黏结模型(linear contact bond model)。颗粒的细观参数通过建立数值双轴试验模型进行反演试算获得。周建等[22]指出，在PFC2D中模拟双轴试验时L/R(L为数值模型的短边尺寸,R为颗粒平均粒径)不能太小，一般应保证L/R>30，这样才能将颗粒的尺寸效应降到最低。本文数值双轴试样尺寸为0.5 m×1.0 m(宽×高)，加载方式为伺服加载，伺服围压分别为50 kPa、75 kPa和100 kPa。加载应力-应变曲线如图3(a)所示。取应力-应变曲线峰值为破坏点绘制摩尔破损应力圆，结果如图3(b)所示。颗粒流模型细观参数见表2。

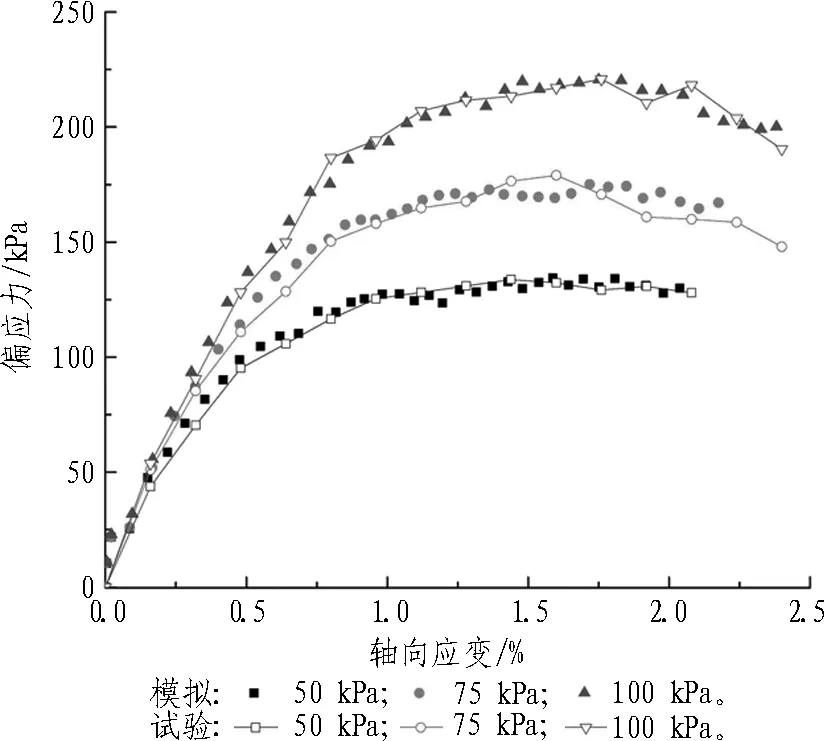
(a) 加载应力-应变曲线 (b) 摩尔破损应力圆

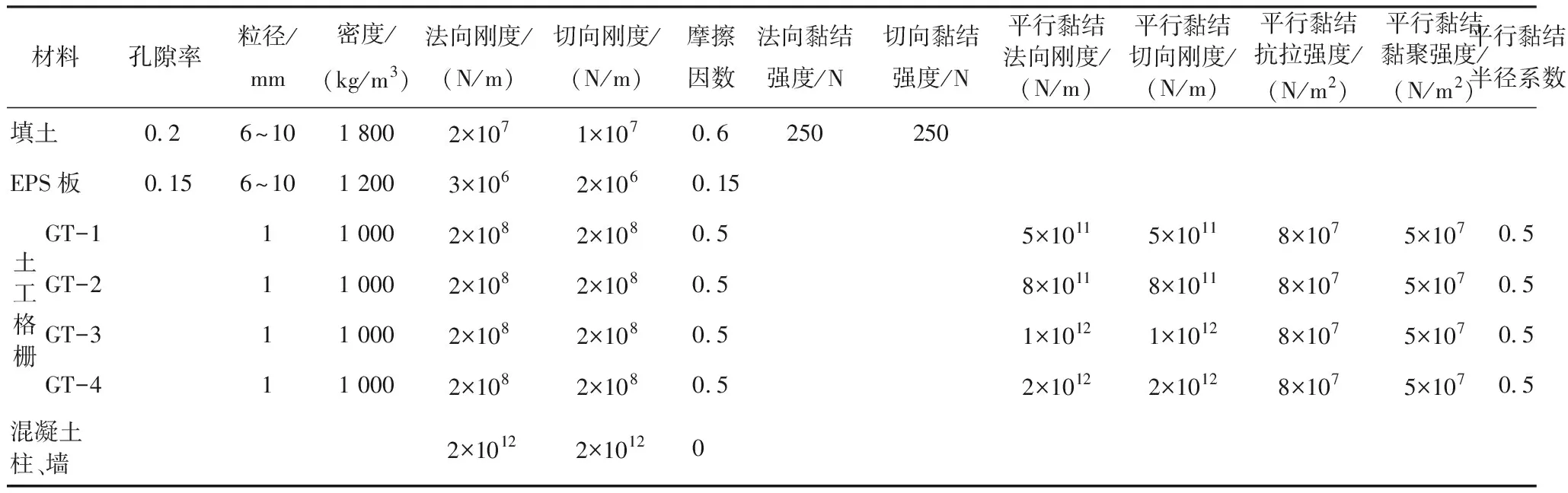
图3 颗粒流双轴试验模拟结果

EPS板室内试验为无侧限压缩试验，其压缩模量为0.98 MPa。数值模拟选择PFC2D内置的线性模型(linear model)作为组成EPS板的颗粒间的本构模型，颗粒粒径服从标准正态曲线分布，通过建立数值压缩试验对其细观参数进行标定，试样尺寸为0.4 m(宽)×0.8 m(高)。经过多次试算，最终确定如图4所示的应力-应变曲线，相应细观参数见表2。由图4可知： 当EPS板的应变在4%以内变化时，DEM曲线与EPS板室内无侧限压缩试验曲线吻合较好。事实上，在进行数值模拟时，EPS板的应变远小于4%。因此，本文采用表2中的EPS板细观力学参数来表征其宏观力学行为[23]。

模拟土工格栅材料时，颗粒间的接触模型采用平行黏结接触本构模型(linear parallel bond model)，并利用格栅拉伸试验的颗粒流模拟确定其细观参数。格栅长100 mm，单个颗粒直径为1 mm，共包含100个颗粒。格栅的数值拉伸试验通过对格栅两端最外缘的2个颗粒各施加10-8m/步的、恒定的、方向相反的速度来实现[18]，同时记录两端的2个颗粒力与位移的关系，将数值试验结果与《产品规格书》中所选的4种土工格栅(见表3)进行对比[20]。经试算，土工格栅细观参数如表3所示。土工格栅拉伸颗粒流模拟曲线与试验曲线对比如图5所示。由图5可知，模拟曲线和试验曲线比较吻合，表明所取的土工格栅细观参数基本可以模拟土工格栅的受拉情况。

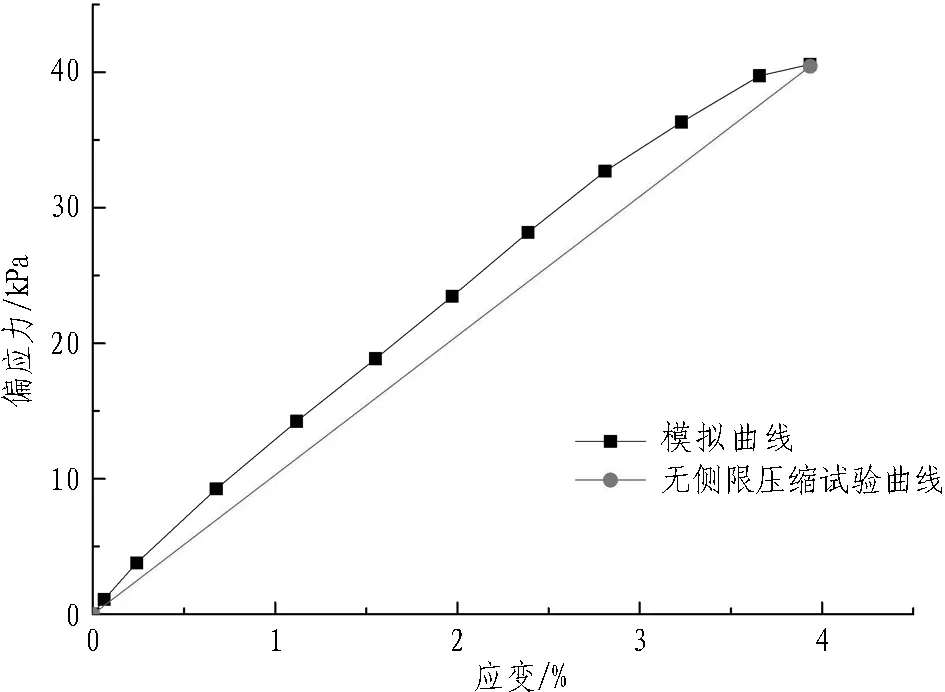
图4 EPS板压缩模拟曲线和试验曲线比较

Fig. 4 Comparison between DEM and experimental results for EPS in a compression test

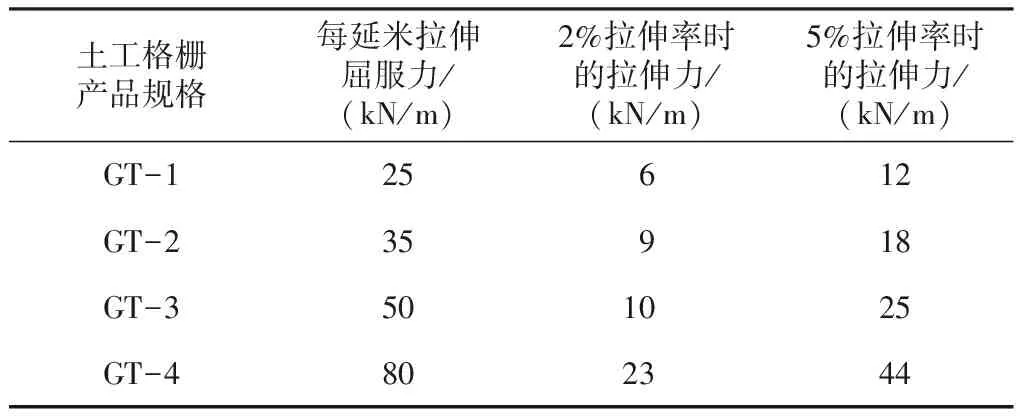
表3 土工格栅产品规格及性能参数

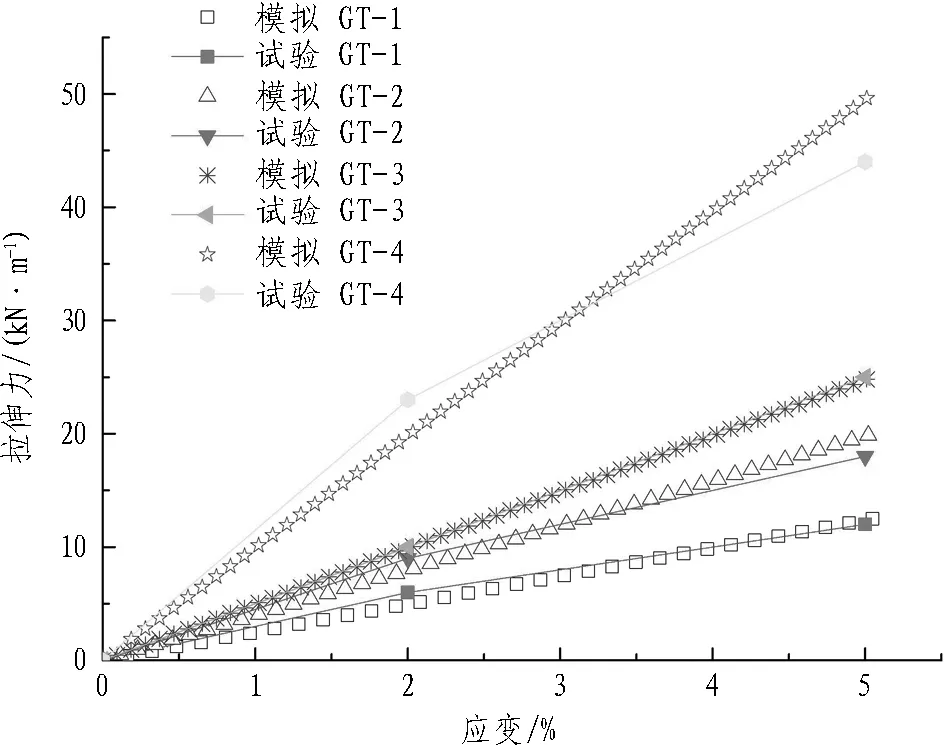
图5 土工格栅拉伸颗粒流模拟曲线和试验曲线对比

Fig. 5 Comparison between DEM and experimental results for geogrid in a tensile test

2 结果分析

2.1 接触力分析

土体中荷载传递通过接触力来体现，荷载的大小和传递方向由接触线条的粗细及其网络结构形式决定。图6示出不同减载措施下颗粒间接触力的分布。图中黑色和红色分别表示压力和拉力，出现拉力是因为填土本身就具有黏性，颗粒间存在黏聚力。YYX1工况下拱顶接触力相比明洞两侧接触力分布密集，接触线条较粗，颗粒间接触力较大。明洞上方一定位置处铺设土工格栅后(工况YYX2)，与工况YYX1相比，颗粒间接触力的分布并未发生明显变化，拱顶接触力分布仍较为集中，格栅并未起到减载作用。为了凸显并加强格栅的减载作用、减小明洞洞顶的接触力，在明洞两侧边坡处设置混凝土柱，即工况3。将工况YYX3与工况YYX2相比，洞顶接触力有了一定程度的减小，明洞两侧的接触力也显著减小；混凝土柱之间的格栅开始受拉(图6(c)中格栅颗粒间接触力变为红色)，其拉膜效应开始显现。这是因为： 1)与填土和格栅相比，混凝土柱的刚度很大，当荷载向下传递时，有相当一部分荷载会转向混凝土柱，使得混凝土柱上的接触力分布较密集，而其他区域内的接触力分布较少； 2)混凝土柱有效限制了明洞两侧土体的下沉，间接增大了内土柱的沉降，内外土柱沉降差迫使格栅发生一定的向下变形。虽然这种情况下格栅发挥了一定的作用，拱顶受力也有所减小，但是拱顶分布的荷载仍大于明洞两侧分布的荷载。为进一步减小拱顶受力，充分发挥土工格栅的拉膜效应，在工况YYX3的基础上增加EPS板作为变形层，即工况YYX4。此时，洞顶上方形成明显的土拱区域，土拱效应明显，拱顶接触力显著减小，土工格栅明显受拉，尤其是EPS板宽度区域内的格栅，受拉更加明显，如图6(d)中局部放大图。

2.2 应力分析

图7示出不同减载措施下竖向应力沿深度方向(图2中测量圆⑥、—位置处)的变化规律。由图7可知: 1)YYX1、YYX2、YYX3工况下竖向应力随深度的增加逐渐增加，在填土顶面以下0.6 m(拱顶以上0.4 m)范围内，竖向应力基本随着深度线性增加； 在0.6 m以下，竖向应力随深度呈曲线变化，竖向应力的增幅逐渐减小。2)工况YYX4的竖向应力随深度的增加逐渐增加，并在深度为0.6 m时达到最大值，随后急剧减小，出现土拱效应，此高度即为土拱高度，土拱高度与明洞宽度之比为2.0。 3)比较工况YYX1与YYX2，填土顶面以下0.8 m范围内，二者竖向应力变化曲线基本重合，竖向应力无明显差别，但在0.8 m以下越靠近拱顶的位置，工况YYX2比YYX1的竖向应力越大。4)对比YYX2、YYX3、YYX4工况下的竖向应力可知，各减载措施的减载效果由强到弱为YYX4>YYX3>YYX2。

(a) YYX 1工况(无减载)

(b) YYX 2工况(土工格栅减载)

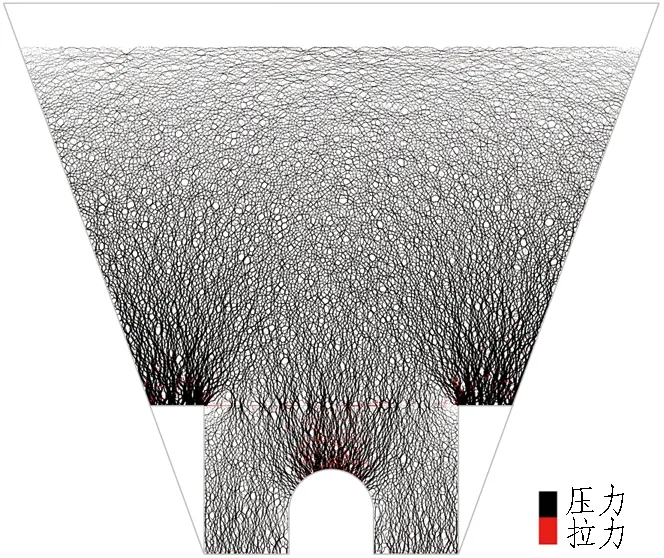
(c) YYX 3工况(土工格栅+混凝土柱减载)

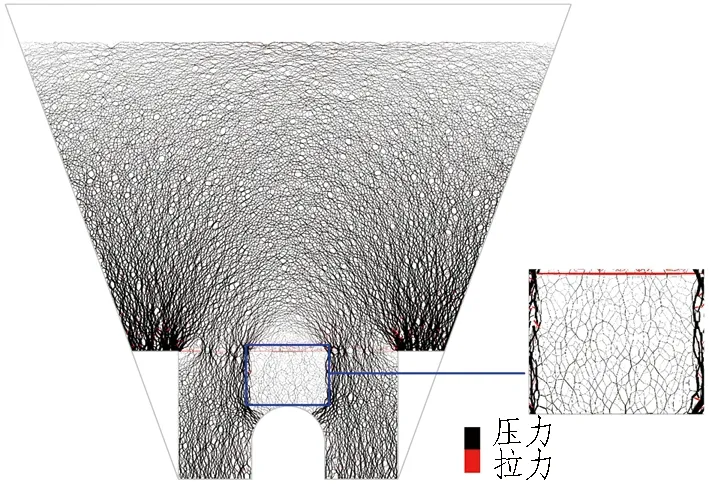
(d) YYX 4工况(土工格栅+混凝土柱+EPS板减载)

Fig. 6 Distribution of contact force between particles under different unloading measures

图8示出不同减载措施下紧靠明洞洞顶上方位置处竖向土压力的变化规律。由图8分析可知： 1)工况YYX1和YYX2的竖向土压力总体相差不大，YYX2工况下拱顶位置处的竖向土压力比YYX1工况下大，这与图7得出的结论相一致。这是由于仅在拱顶上方铺设土工格栅时，格栅限制了明洞拱顶上方土体的沉降，而其两侧土体的沉降受格栅的影响不大，相当于间接增加了外土柱的沉降，进而增加了外土柱对内土柱向下的摩擦力，故对工况YYX1而言，仅铺设土工格栅并不能起到洞顶卸荷作用，反而会增大洞顶受力。2)与工况YYX2相比，工况YYX3洞顶及明洞两侧的竖向土压力均减小，且减载率为33%，这说明混凝土柱的存在能够帮助格栅发挥作用，可有效减小拱顶及洞侧的土压力。3)当在明洞顶继续铺设EPS板后(工况YYX4)，与工况YYX3相比，明洞洞顶竖向土压力显著减小，且洞顶中心的卸载率为94%，明洞上方两侧的竖向土压力增大。这是由于：①EPS板具有压缩变形大的特点，洞顶内土柱沉降远大于外土柱的沉降，洞顶上方出现土拱效应；②EPS板发生较大的向下变形，使得土工格栅中部变形较大，格栅的拉膜效应显著增强。基于以上分析可知，洞顶大部分荷载通过土拱效应和格栅的拉膜效应向混凝土柱转移，少部分荷载向明洞两侧转移。

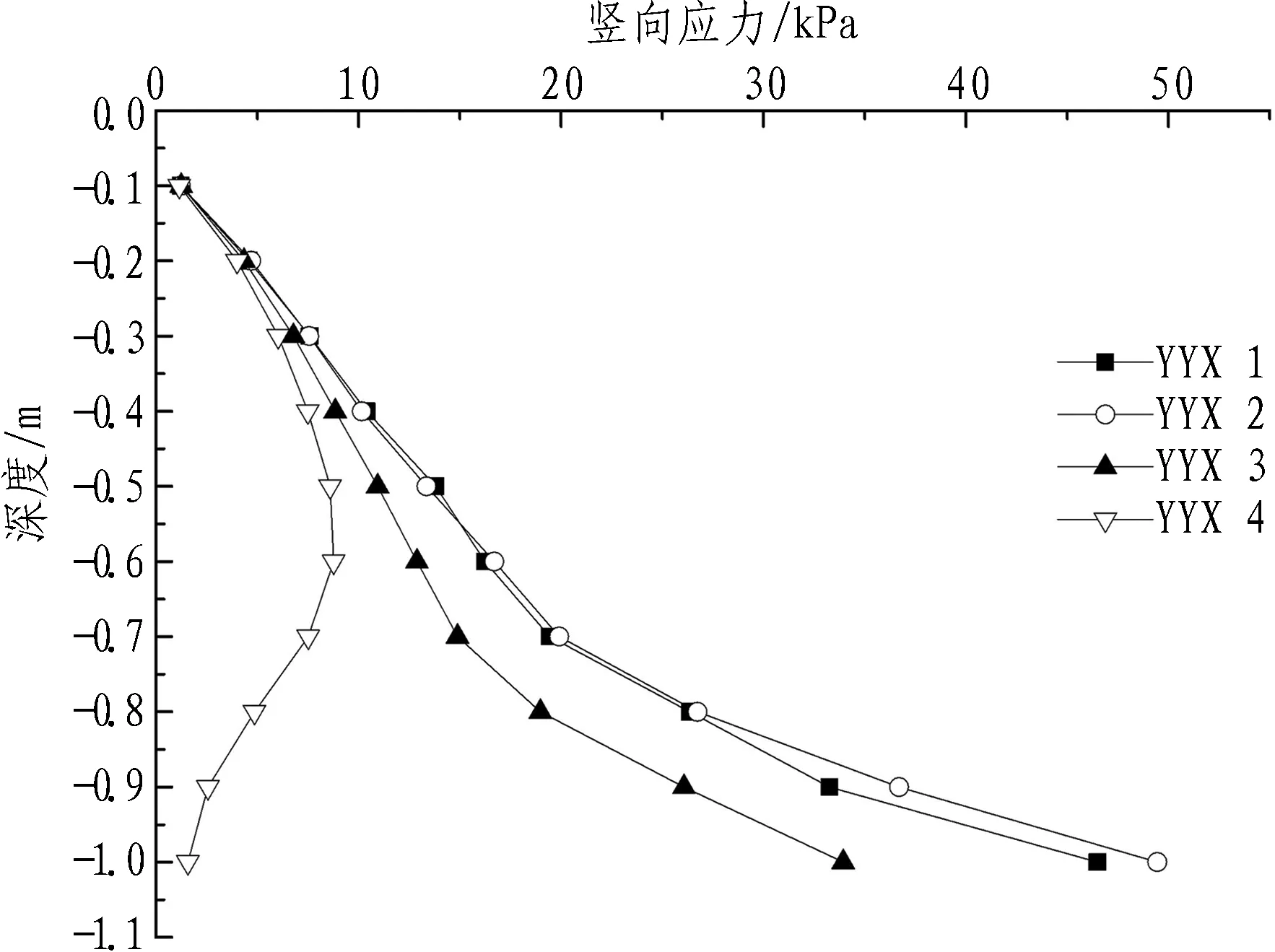
图7 不同减载措施下竖向应力沿深度方向的变化规律

Fig. 7 Variations of vertical stress along depth under different unloading measures

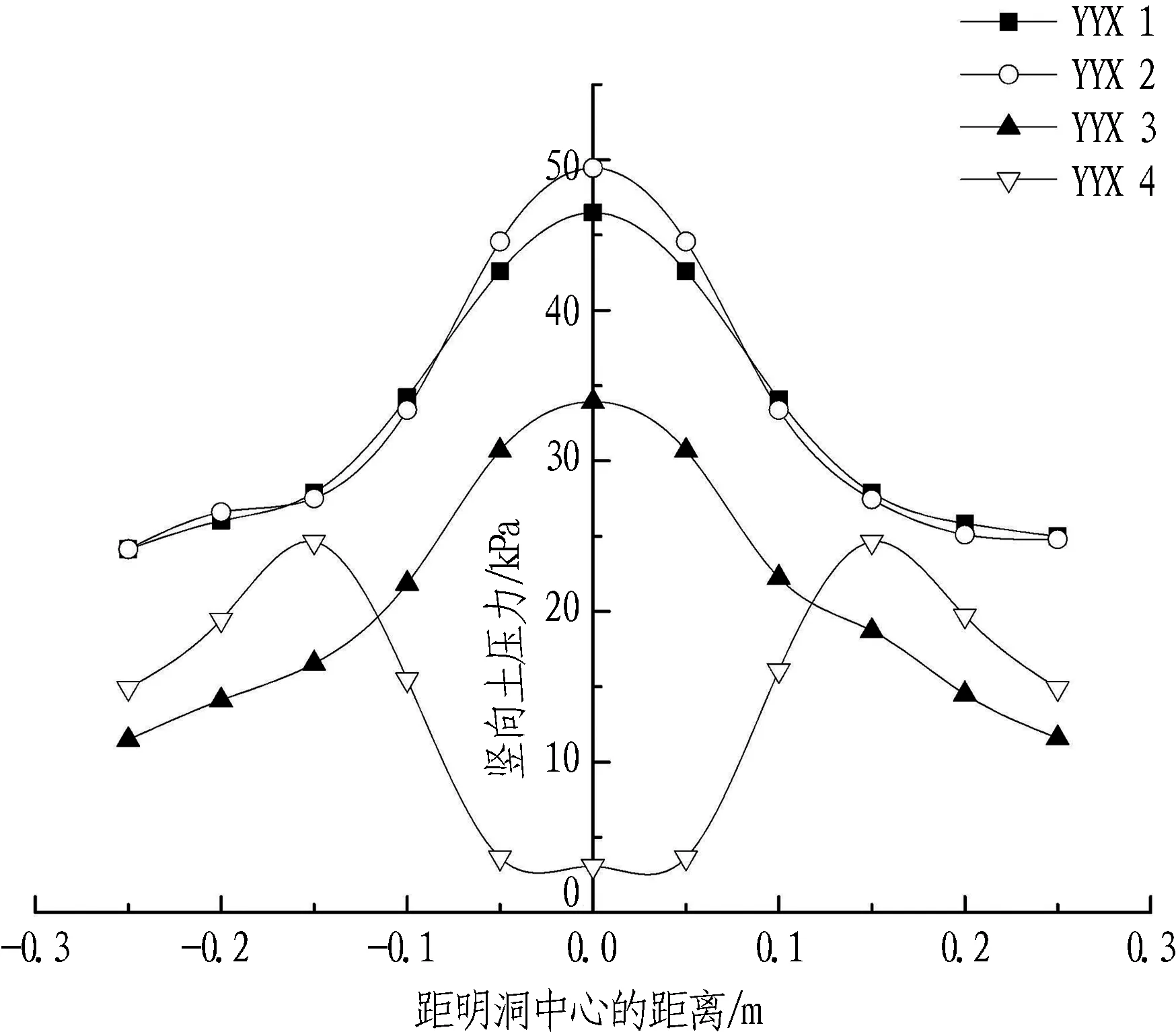
图8不同减载措施下紧靠明洞洞顶上方位置处竖向土压力的变化规律

Fig. 8 Variations of vertical earth pressure on top of open-cut tunnel under different unloading measures

2.3 竖向位移分析

图9示出不同减载措施下明洞洞顶颗粒的竖向位移变化规律。由图9可知，随着减载措施不断改进，颗粒竖向位移逐渐由倒V型向正V型过渡，且基本左右对称。YYX1和YYX2工况下明洞中心颗粒竖向位移最小，两侧的颗粒竖向位移最大，对应的颗粒相对竖向位移分别为0.06 mm和0.07 mm，明洞顶内外土柱沉降差为正值，外土柱对内土柱产生向下的摩擦力，且正的沉降差越大，洞顶土压力越大(见图8)。工况YYX3和YYX4情况下颗粒位移变化都是中间大两边小，对应的颗粒相对竖向位移分别为-0.07 mm和-0.28 mm，此时，明洞顶内外土柱沉降差为负值，内土柱受到外土柱向上的摩擦力，且负的沉降差越大，洞顶荷载转移越多，洞顶受力越小。

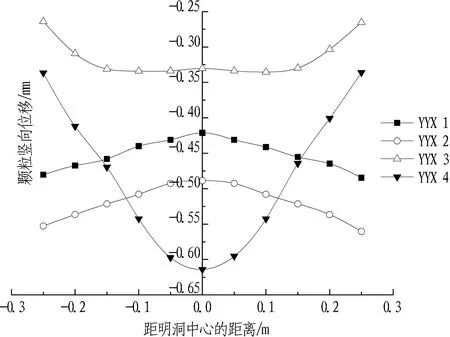
图9 不同减载措施下明洞洞顶颗粒的竖向位移变化规律

Fig. 9 Variations of vertical displacement of particles on top of open-cut tunnel under different unloading measures

图10示出不同减载措施下土工格栅的竖向位移变化规律。由图10分析可知： 1)土工格栅变形左右对称，减载措施不同，格栅的变形也不相同。2)YYX2工况下格栅的竖向变形两边大中间小，其竖向相对变形量为0.12 mm，这是由明洞两侧土体沉降大于中间土体沉降而导致的。3)YYX3和YYX4工况下格栅的最大竖向变形出现在格栅中间，格栅两侧变形基本接近于0。4)YYX3工况下，由于混凝土柱的存在，格栅两侧变形及明洞两侧土体沉降被限制，间接增大了内土柱的沉降，为格栅向下变形创造了有利条件，使格栅的拉膜效应得以显现，此时，格栅的变形主要发生在混凝土柱之间，且变形较缓慢，其竖向相对变形量为 -0.32 mm。5)YYX4工况下，格栅的竖向变形进一步增大，其竖向相对变形量达到-0.6 mm，最大变形发生在EPS板宽度范围内。这是因为EPS板在其上覆填土作用下能够产生较大变形，为格栅向下变形提供很大的空间，格栅的拉膜效应得到进一步加强，此时格栅的减载效果最显著，洞顶土压力最小(如图8所示)。

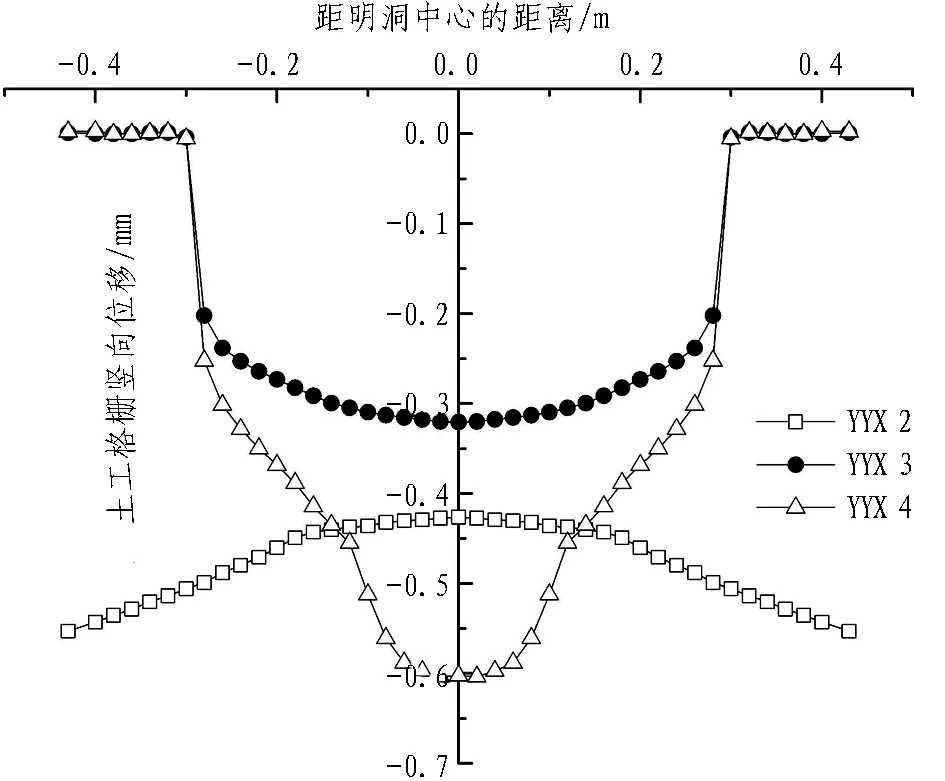
图10 不同减载措施下土工格栅的竖向位移变化规律

Fig. 10 Variations of vertical deformation of geogrid under different unloading measures

结合图9和图10分析可知： 1)YYX2、YYX3、YYX4工况下土工格栅的竖向位移和颗粒竖向位移变化形式基本保持一致，土工格栅的变形依赖于洞顶内外土柱的沉降差； 2)在格栅所能承受的最大变形范围内，内外土柱负的沉降差越大，格栅的拉膜效应越显著，减载效果越好。

3 参数分析

为进一步研究土工格栅材料参数对高填黄土明洞土压力减载的影响规律，以工况YYX4作为参数化研究的基准，分析土工格栅刚度和层数对明洞土拱效应的影响。土工格栅刚度分别取25、35、50、80 kN/m； 土工格栅分别布置为1、2、3层，且每层间距为5 cm。另外，为方便对下文进行分析说明，此处将混凝土柱上的平均应力与混凝土柱间土体的平均应力之比定义为柱土应力比，记为n。柱土应力比越大，洞顶土压力越小。

3.1 土工格栅刚度的影响

图11和图12分别示出明洞洞顶平均竖向土压力和柱土应力比、土工格栅最大竖向变形和洞顶上方土体孔隙率与土工格栅抗拉强度的关系曲线。结合图11和图12可知： 1)当土工格栅抗拉强度为25～35 kN/m时，平均竖向土压力由6.62 kPa减小到6.45 kPa，柱土应力比由12.4增加到12.8，土工格栅最大竖向变形由0.61 mm增加到0.68 mm，孔隙率由0.143增加到0.145； 2)当土工格栅抗拉强度大于35 kN/m时，平均竖向土压力增大，柱土应力比、土工格栅最大竖向变形和孔隙率均减小。这是因为填土性质和填土高度一定时，抗拉强度为35 kN/m的格栅变形最大，其抗拉强度得以充分发挥，格栅提供的向上提兜作用最大，进而使得洞顶土压力最小，洞顶上方填土内部孔隙率最大。因此，实际工程中利用土工格栅对高填黄土明洞进行减载时，应根据填土高度来选择格栅的强度，以便于充分发挥格栅的减载作用。

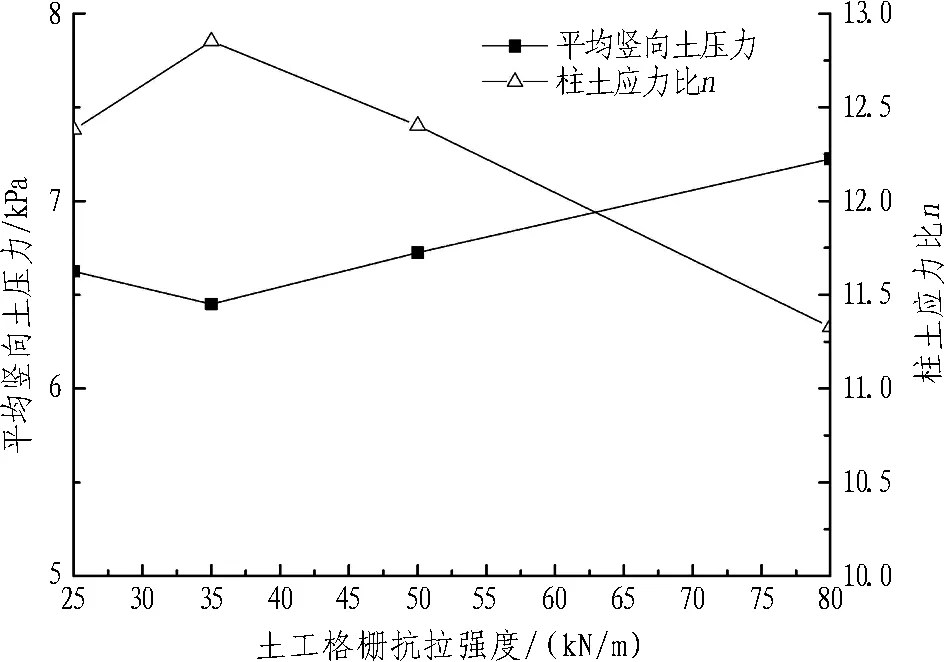
图11明洞洞顶平均竖向土压力和柱土应力比与土工格栅抗拉强度的关系曲线

Fig. 11 Relationship between average vertical earth pressure on top of open-cut tunnel and pillar-soil stress ratio and intensity of geogrid

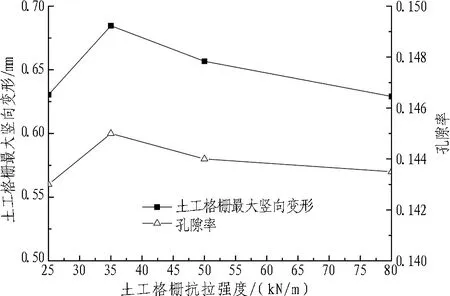
图12土工格栅最大竖向变形和洞顶上方土体孔隙率与土工格栅抗拉强度的关系曲线

Fig. 12 Relationship between maximum vertical deformation of geogrid and porosity and intensity of geogrid

3.2 土工格栅层数的影响

分析土工格栅层数对明洞减载效果的影响时，所指的土工格栅最大竖向变形为最底层格栅的变形。明洞洞顶平均竖向土压力和柱土应力比、土工格栅最大竖向变形和孔隙率与土工格栅层数的关系曲线分别如图13和14所示。由图14可知，填土性质和填土高度一定时，随着土工格栅层数的增加，土工格栅最大竖向变形逐渐增大，并在n=2时达到最大值0.64 mm，随后逐渐减小。由于n=2时，土工格栅竖向变形达到最大值，格栅变形较充分，其提兜作用较明显；此时，洞顶荷载在土拱效应及格栅的提兜作用下逐渐向明洞两侧转移，使得洞顶土压力最小，柱土应力比最大，如图13所示。明洞上方土体孔隙率的变化与洞顶土压力的变化相关。由图14可知，孔隙率随格栅层数的增大先增加，并在n=2时达到最大值0.145，随后开始减小。这是因为n=2时，明洞洞顶上方填土荷载分布较少，洞顶土压力最小。综上，土工格栅层数对明洞减载效果存在最佳值，土工格栅铺设层数应根据具体实际情况来确定。

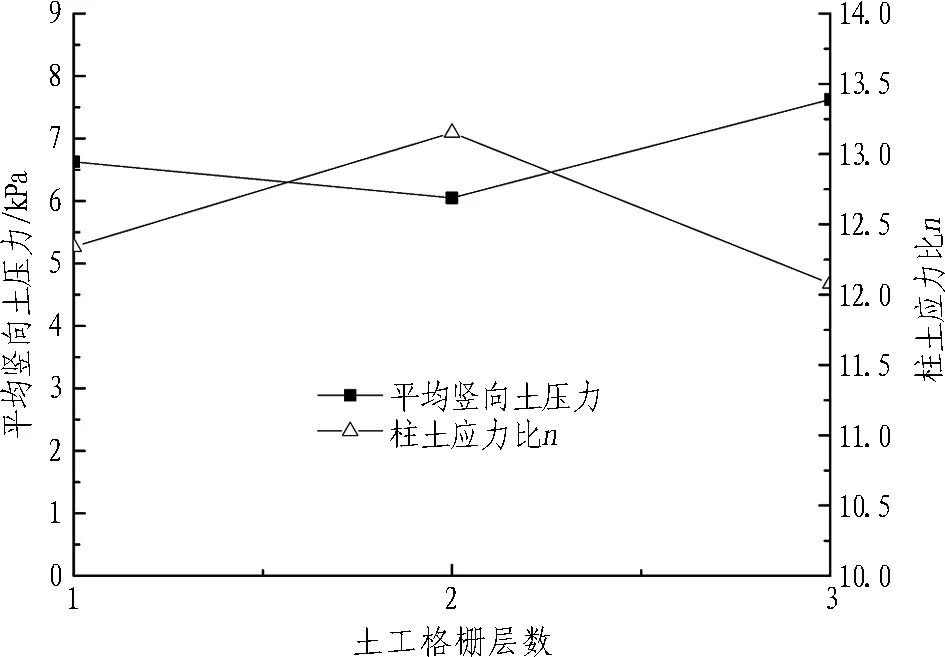
图13明洞洞顶平均竖向土压力和柱土应力比与土工格栅层数的关系曲线

Fig. 13 Relationship between average vertical earth pressure on top of open-cut tunnel and pillar-soil stress ratio and number of geogrid

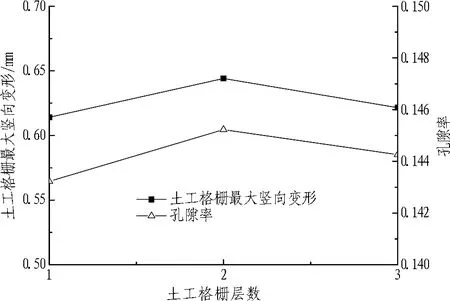
图14土工格栅最大竖向变形和孔隙率与土工格栅层数的关系曲线

Fig. 14 Relationship between maximum vertical deformation of geogrid and porosity and number of geogrid

4 结论与展望

1)仅在明洞顶铺设土工格栅无法起到减载作用，反而会增大洞顶受力；明洞两侧设置混凝土柱时，格栅向下产生一定的变形，拉膜效应凸显，洞顶土压力减小；在格栅底部设置变形层时，内外土柱产生较大的不均匀沉降，格栅的变形更加明显，拉膜效应显著。

2)土工格栅发挥的作用依赖于内外土柱的不均匀沉降，内外土柱沉降差越大，土拱效应越明显，格栅的竖向变形越大，格栅的抗拉强度越能得到充分发挥，拉膜效应越强，减载效果越好。

3)土工格栅的刚度及铺设层数的选择应根据实际填土高度和填土性质来确定。

本文虽然在运用颗粒流分析高填黄土明洞加筋减载方面取得了一定的进展，但研究是在假设地基为刚性地基的基础上进行的，下一步会在针对柔性地基条件下高填黄土明洞土压力的变化规律进行更深入的研究。