泄洪洞洞顶余幅与补气洞通气平衡特性分析

王孝群，练继建，杜帅群，邵 楠，张 剑

(1.河北工程大学水利水电学院，河北 邯郸 056038；2.河北省智慧水利重点实验室，河北 邯郸 056038；3.天津大学水利工程仿真与安全国家重点实验室，天津 300072；4.中国电建集团贵阳勘测设计研究院有限公司，贵州 贵阳 550081)

泄洪洞通风补气问题是工程界一直十分关注的问题，尤其对于我国高坝工程中的高水头长泄洪洞，通风洞内的风速超过规范的现象屡见不鲜。在泄洪洞无压段，水流拖曳其上方洞顶余幅空间内的空气流向下游并由泄洪洞出口流出，导致洞顶余幅空间内形成真空负压，为此实际工程中通常在无压段设置补气洞。在外部大气压与洞顶余幅内的真空负压之间的压差驱动作用下，一定量的空气由补气洞流入洞顶余幅，从而改善洞顶余幅内的气流气压条件。然而若通气孔设置不合理，泄洪洞通风不畅，可能导致洞内负压过大，进而可能引起闸门振动[1-2]、加剧水流紊动或增大空化空蚀破坏[3]风险。

过去的补气洞设计中，首先利用经验公式预测泄洪洞需气量，再根据需气量预测结果确定补气洞的尺寸。韩立[4]对以往研究中提出的各种泄洪管道需气量预测公式进行了总结。然而，以往研究提出的公式大多数来自于特定工程的实测资料或模型试验，仅仅将泄洪洞需气量与泄洪流量、水流弗劳德数等相关联，计算公式相对简单，应用于实际工程时误差较大[5]。此外，三维数值模拟是泄洪洞通风补气结构设计的另一种辅助决策方法，Yazdi等[6]采用VOF方法对明流管道的通气量进行了数值模拟，研究了不同工况下洞内的气流流速分布并给出了计算公式，基于此给出了通气孔尺寸设计的计算方法；李美玲等[7]通过三维数值模型模拟了通风面积对泄洪洞需气量的影响，给出了需气量随通气孔面积的变化规律；Salazar等[8]采用颗粒有限元法(PFEM)模拟了西班牙Susqueda大坝工程底孔泄流中的水-气相互作用，通过模拟计算不同的闸门开度工况，可得到Sharma[9]在试验中观测到的各种流态，且最大需气量出现在80%的闸门开度工况，这与前人的研究结果相符[10]。Wei等[11]利用VOF模型模拟了一个矩形断面有压接无压泄水管道及其通风结构，研究了来流流速及洞顶余幅对通风量的影响，并拟合了通气孔风速的经验公式。然而，对于高水头长泄洪洞这类大尺度复杂结构，三维数值模拟中绘制网格工作量大，且由于需要的网格数量较多导致紊流数值模拟所需的时间较长，尤其在工程设计阶段，结构体型频繁变化导致三维数值模拟的工作量和所需时间倍增。相比之下，Lian等[12]将泄洪洞中的水流视为水-气分层流，推导了泄洪洞多补气洞供气理论分析模型，该模型具有计算效率高，精度高的特点，且补气洞通风量计算通过锦屏一级泄洪洞原型观测结果进行了验证。

泄洪洞通风补气特性十分复杂，泄洪洞的需气量不仅与水流条件有关，可能还与洞顶余幅的面积以及补气洞的结构布置等因素相关。目前需气量、洞顶余幅以及补气洞之间的平衡关系尚不明确，工程界通常认为洞顶余幅总是越大越有利，而本文基于文献[12]给出的泄洪洞多补气洞供气理论分析模型，以锦屏一级泄洪洞为例，进一步模拟分析洞顶余幅和补气洞之间的平衡特性。

1 泄洪洞通风补气系统理论分析模型

若将泄洪洞内的水流视为水-气分层流，则可基于质量守恒和动量守恒的基本原理，分别列出水流和气流的控制方程，再引入分层界面上的水-气拖曳力模型，将水流和气流的控制方程耦合在一起求解。首先，如图1所示进行泄洪洞无压段的空间离散，假定共设置m条补气洞，则以补气洞和泄洪洞出口为节点，将整个泄洪洞划分为m大段，再用适量的节点将每个大段分为适量的微元段，在节点上定义变量，例如：节点i处的断面平均水流流速vwi、洞顶余幅平均气流流速vai和气压pai，补气洞j内的风速vadj和气压padj，即可在微元段上列出控制方程。

图1 泄洪洞明流段水-气分层流空间离散示意图

泄洪洞水-气分层流一维模型中所列的控制方程类似于水力学中恒定总流的控制方程，以下简要介绍水流和气流的控制方程。以节点i和节点i+1为例，水流的控制方程为

(1)

其中ΔHi=Δhfi+Δhawi

式中：yi为节点i处断面底板高程；ρw为水的密度；hwi为断面i处的水深；ΔHi为水头损失；Δhfi为断面i到断面i+1避免摩擦导致的水头损失；Δhawi为水-气拖曳力作用造成的损失，可参考文献[12]；θ为底板与水平面的夹角；g为重力加速度。

气流的控制方程为

(2)

vaiAai=va,i+1Aa,i+1

(3)

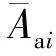
此外，对于补气洞上游侧的节点，考虑气流控制方程时需要考虑补气洞局部质量和能量输入的影响，所列控制方程与式(2)(3)略有差异，更具体的方程推导过程以及水-气耦合求解方法可参考文献[12]。

2 模型验证

本文通过锦屏一级泄洪洞和糯扎渡右岸泄洪洞2个泄洪通风系统验证多补气洞供气理论分析模型的可靠性。

锦屏一级泄洪洞明流段采用弧形闸门连接。图2为泄洪洞闸室和明流段结构示意图，沿程共布置4个掺气挑跌坎；洞身通过3个补气洞与外界大气相连，其中1号洞截面积为21.24 m2，2号洞为32.98 m2，3号洞为32.82 m2。洞身总长1 407 m，其中明流段长约800 m，底板落差约140 m，洞身断面宽13 m，高17 m。当库水位为1 879.35 m时，闸门全开工况下的泄洪流量约为3 220 m3/s[15]。

图2 锦屏一级泄洪洞通风补气系统布置

糯扎渡右岸泄洪洞隧洞长1 076.104 m，工作闸门前有压段长526.749 m，闸门运行水头高达 120 m，设2个闸孔，单孔5 m×8.5 m。如图3所示，明流段共设置了4个通风设施：闸室位置的闸门下游侧设一条通风洞，长约224 m，断面为6 m×6 m的矩形；每道掺气坎处设通气井，断面均为圆形，直径均为2 m，其中，1号和2号通气井还搭配有通气平洞以连接外部大气。当上游水位高程为803.73 m，闸门开度20%时，泄洪流量为705 m3/s[16]。

图3 糯扎渡右岸泄洪洞通风补气系统布置

对锦屏一级和糯扎渡右岸泄洪洞进行空间离散，将对应节点的泄洪洞洞身截面参数、补气洞的结构参数等输入多补气洞供气理论分析模型，计算得到各补气洞或补气竖井的通风量，并与原型观测成果对比(表1)。可以发现，文献[11]预测的锦屏泄洪洞通风量与闸门下游侧的1号补气洞的通风量接近，而本文模型可预测所有通风洞的风量，且计算结果与实测结果十分接近。

表1 通风量计算结果与原型观测结果对比

3 模拟结果与分析

洞顶余幅一直是泄洪洞设计中十分重要的参数，它表示水面以上的空间余量。一般用洞顶余幅面积占泄洪洞断面面积的百分比来表示。若洞顶余幅太小，则泄洪洞内可能出现明满流交替的现象；若洞顶余幅太大，则将造成经济上的浪费。事实上，洞顶余幅很大程度上影响了泄洪洞内的负压。泄洪洞内空气负压条件对泄洪水流稳定性和水流掺气有重要影响。极端工况下，当洞内负压在局部空间范围内剧烈变化，洞内气压作为泄洪水流的自由液面边界条件，将导致水面线的剧烈波动，出现不利流态。若洞内负压过大，则影响掺气设施的效果。

本文以锦屏一级泄洪洞为例进行分析。多补气洞供气理论分析模型中，除可得到各通风设施的通风量外，还可得到水流流速、洞顶余幅风速和气压的沿程变化如图4所示(闸门全开工况)。水流流速在桩号590～1 000 m附近由于底板高程变化不大，水流流速缓慢升高，而在高程变化较大的1 000～1 300 m附近，水流流速迅速升高，最终在泄洪洞出口附近达到约55 m/s。洞顶余幅风速的变化趋势与水流流速变化有关，在水流流速迅速升高的地方，由于水深迅速减小，洞顶余幅空间增大，洞顶余幅的断面平均风速随之减小，而在补气洞位置处，由于补气洞的局部质量和能量输入，风速突然跃升，整个泄洪洞无压段内，气流流速小于水流流速，即水气之间的相互作用表现为水拖气。洞顶余幅内的气压沿程逐渐增大，直至泄洪洞出口附近接近大气压0，而在补气洞位置处，由于补气洞的质量和能量输入，局部风速的突增导致气压的突降。

图4 本文模型计算结果

3.1 洞顶余幅对通气特性的影响

为研究洞顶余幅的影响，通过将锦屏一级泄洪洞的截面高度乘以一定的缩放系数，忽略截面高度对泄流水深的影响(对于多数非极端工况，水深受负压影响较小，计算洞顶余幅时可以忽略)，即可实现洞顶余幅的变化。由于不便直接对比不同截面高度下洞顶余幅气压沿程变化的整个曲线(图4(b))，因此取图中泄洪洞桩号900 m附近单一断面的洞顶余幅气压进行研究。如图5所示为桩号910.186 1 m位置处洞顶余幅气压和通风量随洞顶余幅的变化。随着洞顶余幅的增大，气压经历了先增大后减小，随后又增大，最后趋近于大气压0。

图5 洞顶余幅气压及通风量随泄洪洞洞顶余幅的变化曲线

本文将洞顶余幅变化的过程分为图5中所标的3个分区和2个极值点，具体分析如下：

a.在分区Ⅰ中，由于水面以上的洞顶余幅空间过小，通气不畅，高速水流拖曳的气流量以很高的流速通过狭小的余幅空间，形成了较高的负压，此时洞顶余幅的过气能力较小，补气洞的通气能力有富余，而随着洞顶余幅的空间增大，洞顶余幅过气能力增大，负压则不断减小；分区Ⅰ内，洞顶余幅的少量变化将引起气压的剧烈变化，且洞顶余幅太小可能造成明满流交替现象，有一定工程风险，设计中应避免洞顶余幅落入该范围；此外，SL 279—2016《水工隧洞设计规范》条文5.3.4要求洞顶余幅不小于15%，与本文的17.2%基本相符。

b.在分区Ⅱ中，随着洞顶余幅进一步增大，泄洪洞的总通风量持续增大，即洞顶余幅的过气能力持续增大，此时补气洞的供气能力相对于洞顶余幅的通气需求是不足的，需要以增大泄洪洞内的负压为代价来增大补气洞内外压差，从而提供更大的通气量。分区Ⅱ内，负压随着洞顶余幅的增大而增大(即气压降低)，补气洞的补气能力不足是限制泄洪洞通风补气的主要因素。在分区Ⅱ内，洞顶余幅越小负压越小，即在保证减小负压同时也缩小了泄洪洞的尺寸。

c.在分区Ⅲ中，随着洞顶余幅空间的进一步增大，泄洪洞的总通气量反而有所降低，可见此时泄洪洞内可能形成逆向气流等复杂流态。洞顶余幅内的逆向补气将抑制其对补气洞的供气需求，且由于洞顶余幅增大使断面平均风速降低，洞内的负压自然随之降低。此外，随着洞顶余幅的增大，泄洪洞出口大气压对洞内的抬压作用影响越来越明显，可以设想极限情况下，泄洪洞截面不断加大，洞顶余幅空间无限接近100%，这就相当于开敞明渠流的情况，洞内气压将逐渐接近0，即大气压；在分区Ⅲ内，负压的降低以增大洞顶余幅为代价，牺牲了经济性。

d.在余幅17.2%极值点处，补气洞的供气量恰好满足泄洪洞洞顶余幅过气能力，补气洞通气能力与泄洪洞的需气量达到较好的平衡。补气洞尺寸与洞顶余幅达到最优匹配，实际工程中若按照该极值点进行设计，无疑可同时保证泄洪洞内不产生过大的负压且泄洪洞洞身及补气洞的尺寸均较小，然而实际中泄洪水深沿程变化，若为了让所有隧洞截面保持最优余幅显然不现实。

e.在余幅54.9%极值点处，由于水流的拖气能力有限，随着洞顶余幅增大，通气量增大的程度逐渐放缓，反而增大的过气面积使余幅内的断面平均风速减小，此时洞顶余幅内的通气量已达到极大值。此时，洞顶余幅的需气量与补气洞的供气能力再次达到新的平衡。在该极值点之前，为提高补气洞供气能力而形成的负压起主导作用，在该极值点之后，泄洪洞截面扩大对负压的缓解作用占据优势。以该极值点为界，无论扩大或缩小洞顶余幅，均能实现洞内负压的降低。

3.2 补气洞截面面积与洞顶余幅的平衡关系

由第3.1节分析可知，泄洪洞中水流的拖气能力、洞顶余幅的过气能力以及补气洞的补气能力之间的平衡关系决定了泄洪洞内通风补气的顺畅程度，影响着洞内气压和风速的变化。补气洞的补气能力主要由补气洞的截面面积决定，因此本节将锦屏一级泄洪洞的3条补气洞的总面积Atotal乘以一定的放大系数(1.25、1.5、1.75、2.0)，在不同的补气洞面积下，分别计算图5中的曲线，得到如图6所示的通气量及气压随泄洪洞洞顶余幅的变化曲线簇。

图6 洞顶余幅气压及通风量随泄洪洞洞顶余幅的变化曲线簇

对比图6(a)中曲线，随着补气洞截面面积的增大，泄洪洞需要匹配更大的洞顶余幅才能达到极值点(即平衡点)；此外，随着补气洞截面面积的增大，极值点条件下的负压降低，2个极值点位置的负压越来越接近。换言之，随着补气洞断面面积的增大，洞顶余幅空间内的负压对于泄洪洞洞身截面高度的变化的敏感性降低，即补气洞设置得越大，泄洪洞洞顶余幅空间的适用范围则越大。

对比图6(b)中曲线，在洞顶余幅增大到第1个极值点之前，各曲线基本重合，这是由于在该范围内，洞顶余幅的过气能力是制约泄洪洞通风补气的主要因素；然而，随着洞顶余幅的增大，图6(b)中的各曲线分别在达到图6(a)对应曲线第1个极值点对应的洞顶余幅后相继偏离，补气洞越小，则相应的曲线越早偏离；在洞顶余幅达到第2个极值点之前，泄洪洞的总通风量持续增大，且各条曲线均在达到图6(a)中所示的第2个极值点之后出现转折，通风量随洞顶余幅增大而减小这与3.1节所述规律一致。

4 结 语

a.泄洪水流的拖气能力、洞顶余幅的过气能力以及补气洞的补气能力相互平衡，相互制约。

b.当补气洞截面面积一定时，随着洞顶余幅的增大，洞顶余幅内的气压先增大后减小，最后又增大直至接近大气压，本文将这一过程划分为3个分区和2个极值点；在分区Ⅰ内，洞顶余幅过气能力不足是限制泄洪洞通风补气的主要因素；在分区Ⅱ内，补气洞的补气能力不足是限制泄洪洞通风补气的主要因素；在分区Ⅲ内，泄洪水流自身的拖气能力是限制泄洪洞通风补气的主要因素；在第1个极值点处，补气洞的补气能力与洞顶余幅过气能力达到最优匹配，实际工程中若按照该极值点进行设计，无疑可同时保证泄洪洞内不产生过大的负压且泄洪洞洞身及补气洞的尺寸均较小；在第1个极值点处，无论继续增大洞顶余幅还是减小洞顶余幅，都能使洞内的负压降低，显然，在该极值点处设计，即造成较大的负压，又不经济。

c.补气洞横截面积的增大能使洞内负压对于洞顶余幅变化的敏感性有效较低，因此更大的补气洞能使洞顶余幅的尺寸在更大的范围内灵活设计而不至于对洞内负压造成不利影响。

综上所述，本文建议明流泄洪洞的洞顶余幅与补气洞的结构设计应考虑两者的平衡关系，可利用所述多补气洞供气一维分析模型绘制相应的平衡优化曲线簇，并尽可能在优化曲线中的分区Ⅱ内进行设计，即可在实现泄洪洞通风特性优化的前提下兼顾补气洞以及洞顶余幅尺寸的经济性，实现明流泄洪洞洞顶余幅和补气洞联合优化设计。