闸墩绕流影响因素及其作用规律分析

王志飞, 杨贝宁, 王思莹

(武汉理工大学新材料力学理论与应用湖北省重点实验室，湖北 武汉 430070)

2018年某调水工程运行巡检中发现在某渡槽下游水面有异样起伏，随之产生的非定常力可能给工程运行带来安全隐患。经检测分析，初步推测这种水面起伏与闸墩绕流脱涡有关。为了进一步探明原因并为制定整改措施提供基础支撑，本文开展了针对闸墩绕流影响因素及其作用规律的研究工作。

水利和海洋工程中普遍存在钝体绕流现象。在特定条件下，流体流过钝体时会在其表面发生边界层分离，产生周期性脱落的漩涡，导致钝体受到周期性的非定常力作用，甚至让水中结构产生流激、涡激振动，带来安全隐患。作为钝体绕流问题的典型研究模型，无穷宽流道中的理想圆柱绕流已被广泛研究。该问题的主要控制参数为雷诺数Re。目前科研界对不同雷诺数条件下圆柱绕流的流态和升阻力系数变化规律已达成了一定的共识[1-2]。

实际工程中的钝体绕流现象多为高雷诺数流动，涉及非线性湍流方程的求解，理论分析和数值模拟方法面临一定的挑战。工程结构的大尺度和流动的复杂性使得试验观测也具有一定难度，制约了高雷诺数条件下圆柱绕流研究的发展。随着计算机硬件和数值仿真技术的发展，直接数值模拟(direct numerical simulation, DNS)、大涡模拟(large eddy simulation, LES)、Reynolds平均(Reynolds average Navier-Stokes, RANS)、格子玻尔兹曼(lattice Boltzmann method, LBM)等方法逐渐应用于圆柱绕流问题的研究中，研究成果加深了人们对圆柱绕流机理的认识，推动了类似问题的仿真计算研究。试验和仿真[3-13]结果表明，临界区和超临界区的二维圆柱绕流边界层会产生分离泡现象，流动转捩后产生湍流分离，阻力系数随雷诺数增加显著增加；高超临界区的圆柱绕流边界分离过程差不多，但是无分离泡现象，阻力系数具有雷诺数无关性。但总体而言，对于高超临界雷诺数(Re>3.5×105)条件下的圆柱绕流研究工作少且不系统, 不同的研究成果尚存在一些差异。

除了涉及高雷诺数流动条件，现实工程中的钝体绕流还大多发生在有限宽流道内，流道壁面的存在不仅会影响圆柱周围流场的发展，对剪切层失稳和尾迹动力学都有较大影响[14-22]。除此之外，由于实际条件的限制或者工程布置的需要，现实中的桥墩、闸墩等涉水结构可能处于各种各样的流道中。弯曲流道、变截面流道的存在，使得结构面临的不再是均匀剪切流，绕流产生的流场和受力势必也有所不同。下游弯道对钝体尾涡的影响已有一些研究成果[23-26]，但对非顺直流道中钝体绕流相关的研究还很缺乏，流道布局对绕流流场和结构受力的影响规律还有待进一步研究。从工程应用需求出发，除了圆柱绕流，目前国内外对方柱、椭圆柱的绕流也有一定的研究[27-36]，如考察了方柱导角、椭圆柱展长比等参数对其绕流流场和受力特性的影响。但针对其他形状的钝体绕流研究相对较少，目前尚未形成一致的结论。

本文在Re=5×106的条件下，对布置在各种形式流道中的圆柱绕流和不同形态的闸墩绕流进行了数值仿真研究，分析了流道布局和闸墩形状尺寸等因素对绕流流场和结构受力特性的影响规律。

1 数值模型

1.1 计算模型

本文计算模型参照某水利工程的渡槽建立。该水利工程主渠道宽60 m，渡槽长60 m，宽30 m。上下游分别由长40 m和60 m的渐变段与主渠道相接。闸室采用双闸室设计，中间闸墩厚度为5 m。参照工程布置方案和建筑物尺寸，本文选取圆柱直径D=5 m，基础流道宽度W=6D来建立模型开展分析。

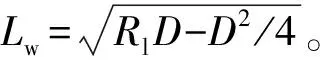
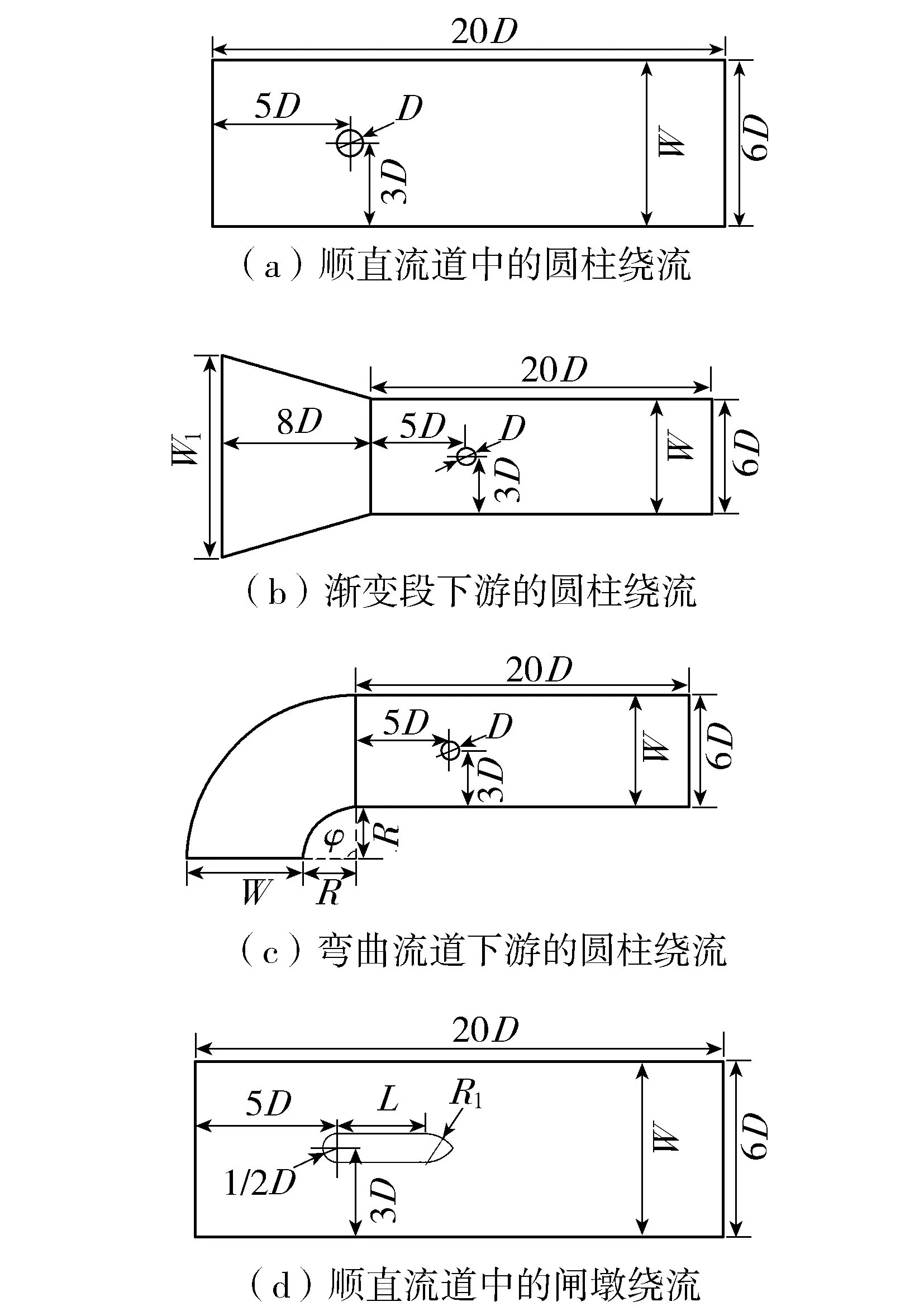
图1 计算模型

1.2 计算方程和参数设置

本文采用COMSOL Multiphysics中的计算流体动力学(computational fluid dynamics，CFD)模块来模拟各种流场环境下的钝体绕流。该模块采用有限元法求解二维或三维流体力学问题。本文选用该模块的k-ω湍流模型进行计算分析。

本文求解的流体力学方程为不可压缩流体的连续性方程和N-S方程：

∇·v=0

(1)

(2)

式中：v为流体的速度矢量；p为流体压强；ρ为流体密度；μ为流体的动力黏度；t为时间。

在特定的边界条件下求解式(1)(2)，即可得到流体域的压力场和速度场，继而对圆柱和闸墩绕流产生的流场和结构受力特性进行分析。高雷诺数条件下，钝体绕流流场主要分析脱涡频率，定义表征钝体脱涡频率的斯坦顿数St为

(3)

式中：f为脱涡频率；D为钝体的特征尺寸, 圆柱绕流中为圆柱直径，闸墩绕流中为闸墩的宽度。

流体中钝体结构受到的流体作用力为

(4)

式中:F1、F2分别为钝体受到的来流方向的合力(阻力)和垂直来流方向的合力(侧向力)；-pI和K分别为流体应力中的压力项和黏性力项；τ为钝体结构的外表面；n为边界处的外法线单位向量；ej为坐标轴方向的单位向量。

以ρ、U、D为特征值，定义钝体的阻力系数Cd和升力系数Cl为

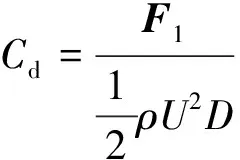
(5)

(6)

计算时将计算域左侧设定为速度入口边界，根据工程运行情况设置入口平均速度U=1 m/s。计算域右侧设定为压力出口边界。圆柱、闸墩和流道壁面设置为无滑移壁面条件。流体介质定义为水，密度ρ=103kg/m3，动力黏性系数为0.001 kg/(m·s)。该流动对应的雷诺数Re=5×106，湍流参数的初始值设置为湍流强度为0.05，湍流长度为0.35 m，湍动能为8.12×10-4m2/s2, 比耗散速率为0.15 s-1。

1.3 模型验证

基于图1(a)的圆柱绕流计算模型，采取图2所示的4种不同网格设置进行计算，分析网格无关性。4种方案的流体计算域都使用结构化网格，设置20层边界层网格，单元增长率为1.1。方案M1最大单元尺寸为1 m，总计237个三角形网格，30 010个四边形网格，共30 247个单元；方案M2的最大单元尺寸为0.5 m，总计432个三角形网格，48 608个四边形网格，共49 040个单元；方案M3最大单元为0.4 m，总计542个三角形网格，64 146个四边形网格，共64 688个单元；方案M4最大单元为0.3 m，总计630个三角形网格，80 482个四边形网格，共81 112个单元。

图2 计算网格

采用4种网格分别对同一算例进行仿真计算，得到圆柱的平均阻力系数分别为0.68、0.67、0.65和0.66，St均约等于0.31。Ong等[36]的试验结果表明，与本算例条件相当的圆柱平均阻力系数范围是0.36～0.75，St范围是0.18～0.50。本文用4种网格计算得到的结果均在此范围之内，验证了本文计算结果的可靠性。综合计算结果精度和计算资源消耗情况，选定方案M3作为本文数值计算的网格划分方案。

基于网格划分方案M3，选取0.02 s、0.05 s、0.1 s、0.2 s 这4种时间步长，对图1(a)圆柱绕流算例进行了时间步长的影响分析。对比结果表明，4种时间步长设置下计算得到的圆柱周围流场结构和圆柱受力都基本一致。综合计算结果精度与计算资源耗费情况，选择0.05 s为时间步长开展后续的计算分析。

2 结果与分析

2.1 流道布局对圆柱绕流的影响

计算得到的流场分布显示，流道壁面靠圆柱越近，壁面对圆柱周围以及尾迹流态产生的影响也越大。从表1可以明确看到，随着流道宽度变窄，圆柱占空比增大，圆柱的平均阻力系数、最大升力系数以及St均有所增大，且增大的趋势越来越明显。这个计算结果的规律性与前人在不同雷诺数条件下得到的结论是一致的[14-22]。

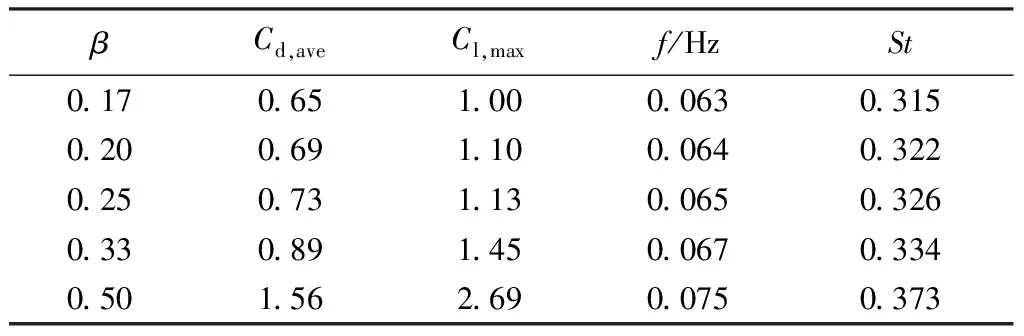
表1 不同宽度流道中的圆柱绕流计算结果

由表2可知，在本文计算参数范围内，渐变收缩段下游流道中的圆柱脱涡频率略微降低，圆柱的最大升力系数、平均阻力系数受到的影响不明显。这与本文计算模型中圆柱所处位置与渐变段之间存在一定长度的顺直流道相关。渐变收缩段让流动产生往流道中间汇聚的分布趋势，但是经过顺直流道的平顺过渡之后，该集中效应减弱，因此圆柱面临的来流与顺直流道中差别不大。实际工程中，渐变段的布置位置一般也会与闸墩等结构隔开一定距离。但根据具体工程布置的需求，闸墩等涉水结构不一定处于流道正中间。因此今后可考虑针对圆柱所处横向位置的变化对其绕流情况的影响开展进一步研究。

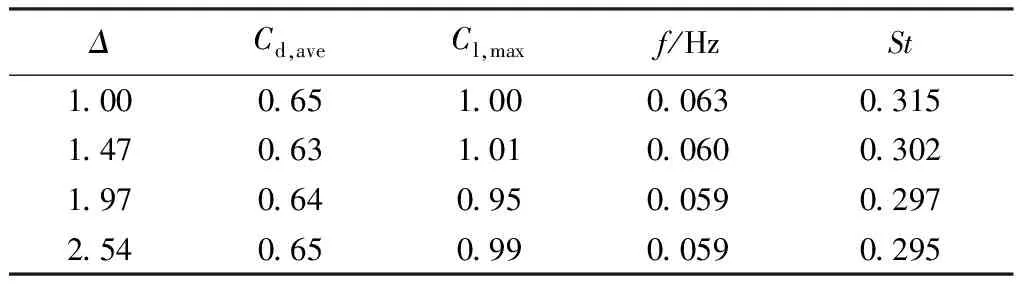
表2 不同渐变段下游的圆柱绕流计算结果

从图3可见弯道使其下游顺直流道各截面的流速分布发生了变化，呈明显的非对称性。靠弯道外侧流速增加，靠弯道内侧流速减小。为了表征流道截面流速分布的非对称程度，定义流道横截面上下两部分平均流速的相对差值为偏流系数α：

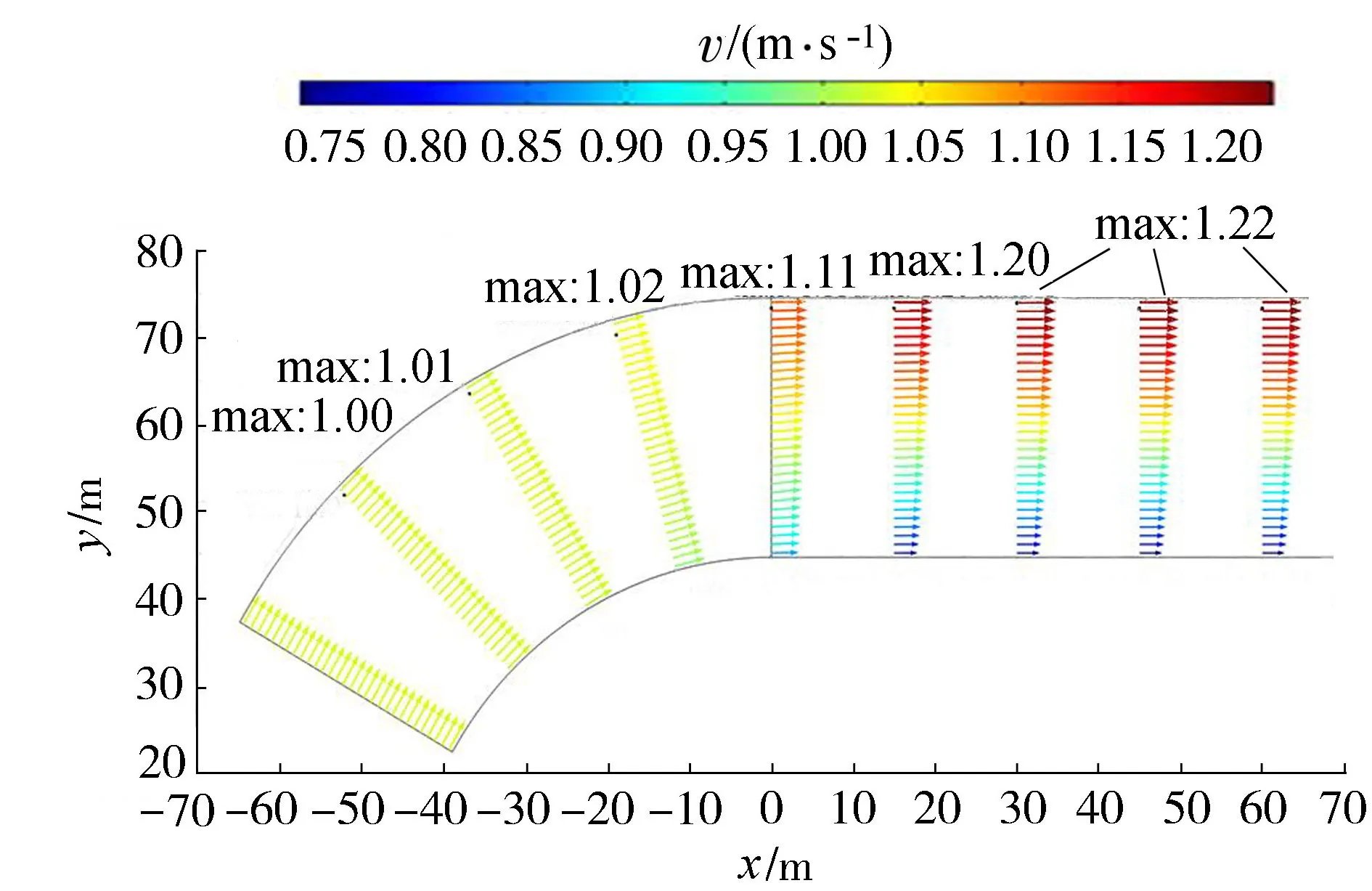
图3 典型弯道中的流速分布(R=9D，φ=60°)

α=(U上-U下)/U

(7)

式中：U上为横截面靠外侧一半流道的平均速度；U下为横截面靠内侧一半流道的平均速度。

图4给出了不同弯道下游流道中偏流系数。由图4可知，在各种弯道作用下，从弯道末端截面开始，下游流道横截面的偏流系数逐渐增加并趋于稳定。对于固定位置截面，上游弯道内径R越小，偏流系数越大，即转弯半径小的弯道会导致下游流道流速分布呈更强的非对称性。由图4(b)可知，对于固定截面，只有弯道转弯角度为30°时，偏流系数偏小，当角度达到60°以上时，转弯角度的增大对下游顺直流道的偏流系数没有明显影响。

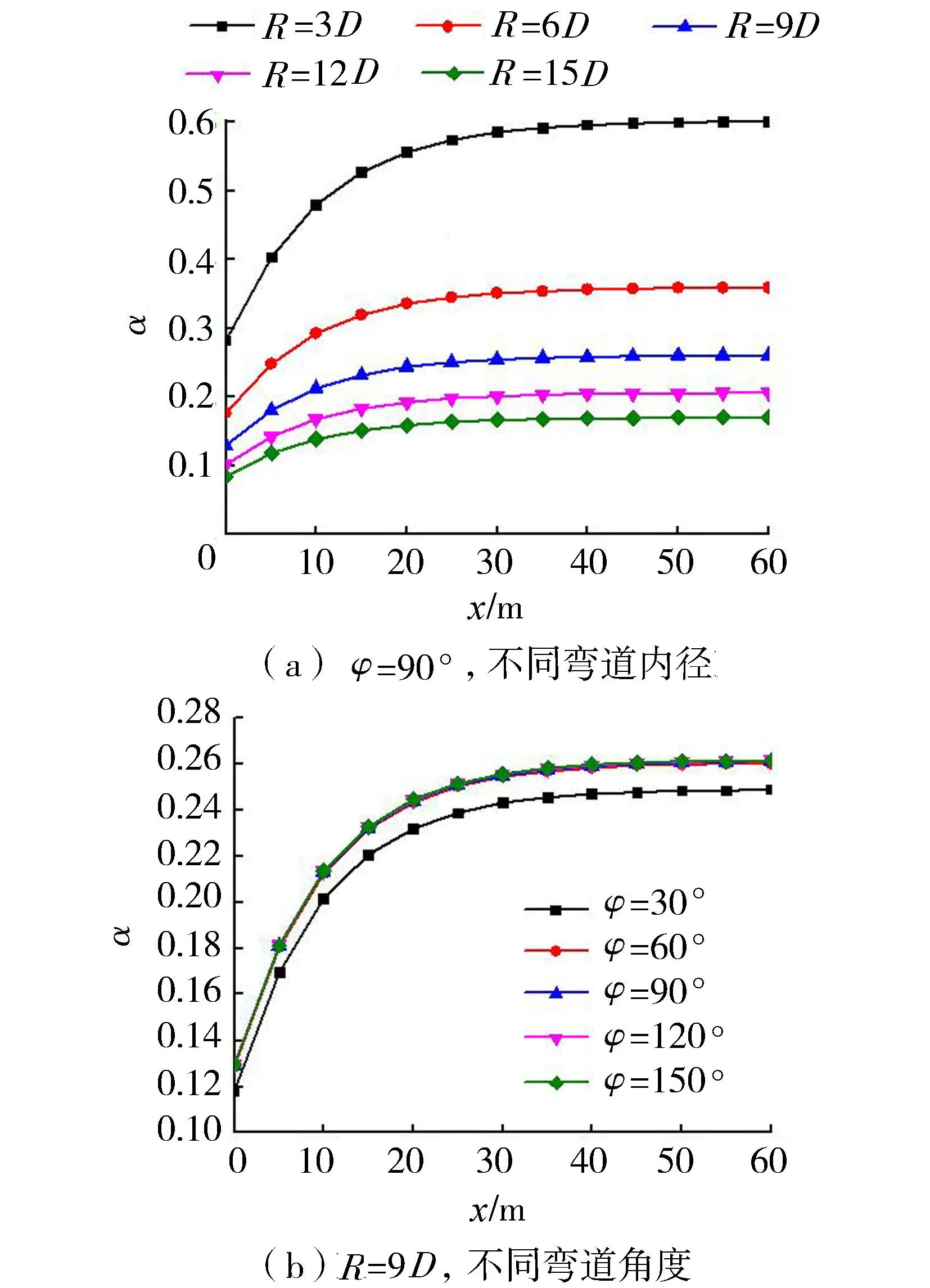
图4 弯道影响下的偏流系数

在弯道导致的非对称流场影响下，流道中圆柱脱涡也呈现出非对称的形态。这种非对称特性在图5所示的升阻力时程曲线中表现得更为直观。与顺直流道中圆柱绕流的升阻力曲线一样，弯道影响下的圆柱升阻力曲线仍然呈周期性变化。但由于弯道的偏流效应，阻力系数的峰值在2个不同的数值之间交替变化，同时升力系数的均值也不再为零。不同弯道布置下，圆柱绕流的受力特征参数如表3所示。可以看出，弯道的存在对圆柱的脱涡频率和阻力系数平均值影响不是很大。但随着弯道产生的偏流效应增加，圆柱的升阻力系数峰值差异和升力系数平均值都有所增加。

表3 弯道对圆柱绕流的影响

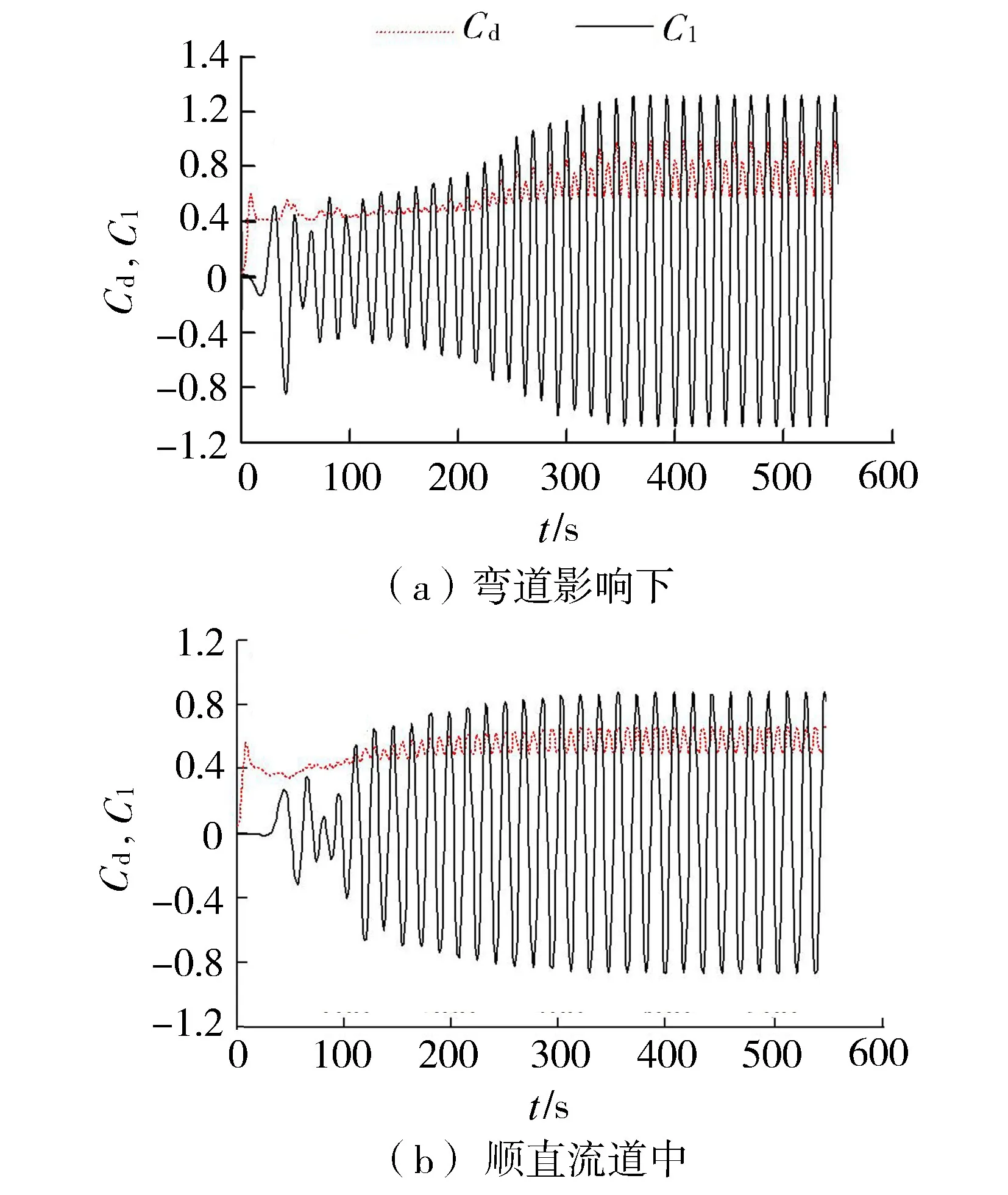
图5 弯道影响下圆柱的升阻力系数

2.2 形状尺寸对闸墩绕流的影响

无墩尾的闸墩绕流产生的涡量场和受力情况与圆柱绕流类似。如图6(a)和图6(b)所示，闸墩后端交替脱落方向相反的旋涡，在下游形成周期性的卡门涡街结构。如图7(a)所示，闸墩受到的升力和阻力呈周期性变化，阻力系数变化的周期是升力系数的2倍。

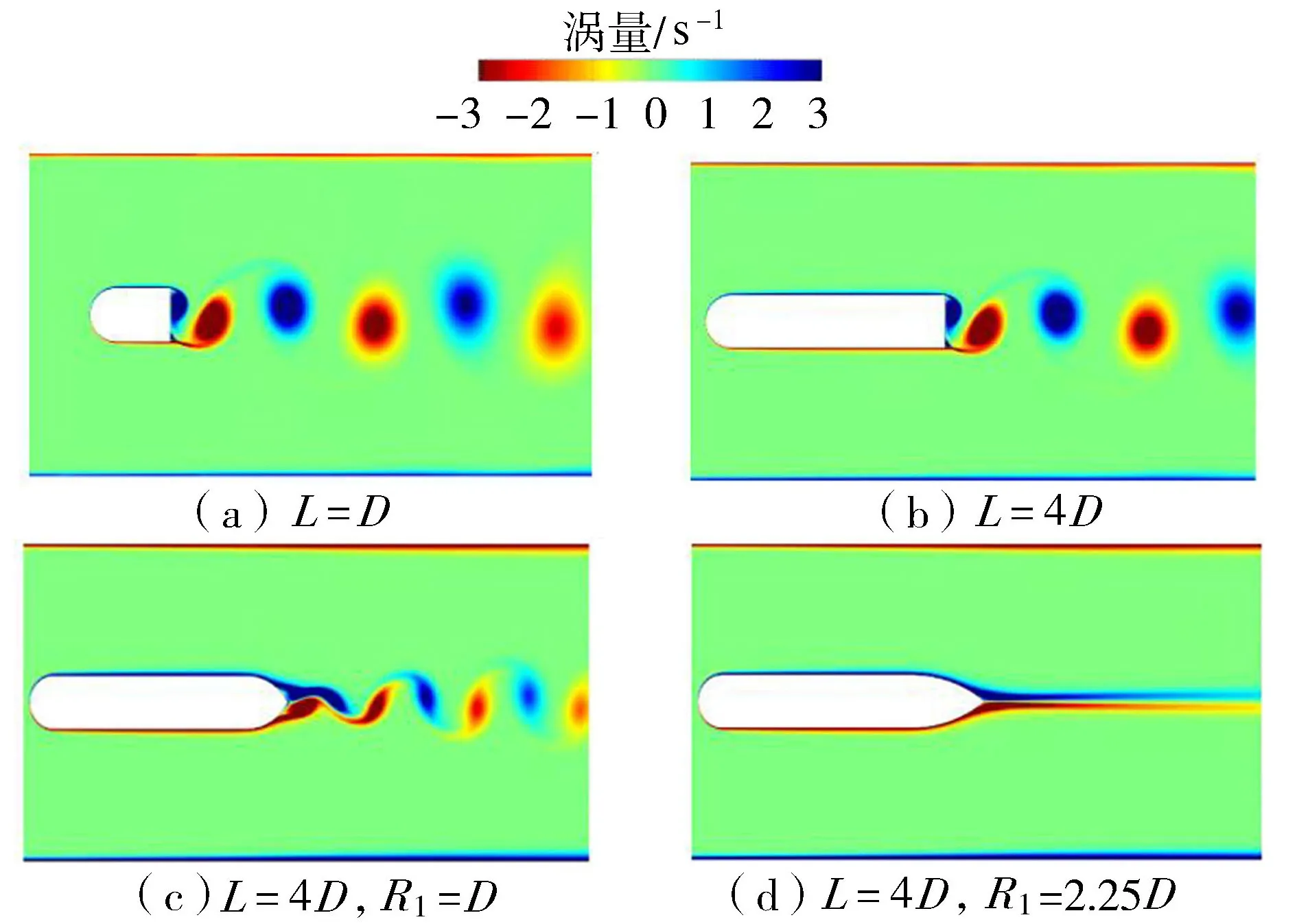
图6 不同闸墩绕流的涡量场

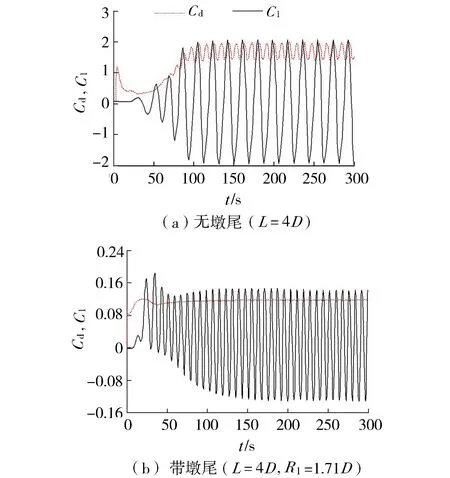
图7 典型闸墩的升阻力系数

带墩尾的闸墩整体呈流线型，其绕流产生的旋涡强度和尺寸均明显小于无墩尾闸墩和圆柱绕流所产生的旋涡强度和尺寸。对于墩尾R1=2.25D的闸墩(图6(d))，其绕流产生的边界层甚至不再分离，墩后不再脱涡。阻力系数趋近于一个常数, 升力系数变化的幅值也明显变小(图7(b))。

由表4可知，随着墩身长度变长，无墩尾闸墩的平均阻力系数减小，最大升力系数增大，脱涡频率和St几乎不变。与无墩尾闸墩相比，带墩尾闸墩的平均阻力系数和最大升力系数都明显减小，脱涡频率和St明显变大。与无墩尾闸墩绕流相同，带墩尾闸墩的升力系数幅值与墩体长度仍然呈线性正相关关系。但不同的是，带墩尾闸墩的平均阻力系数并没有随着墩体长度的增加而减小，反而是呈逐渐增大的趋势，且与墩体长度基本线性相关。这是由于带墩尾闸墩呈流线型，其阻力以摩擦阻力为主，而无墩尾闸墩受到的阻力却是边界层分离引起的压差阻力起主导作用。而摩擦阻力的大小与绕流物体的长度成正比，压差阻力随物体长度增加而产生的变化不明显。

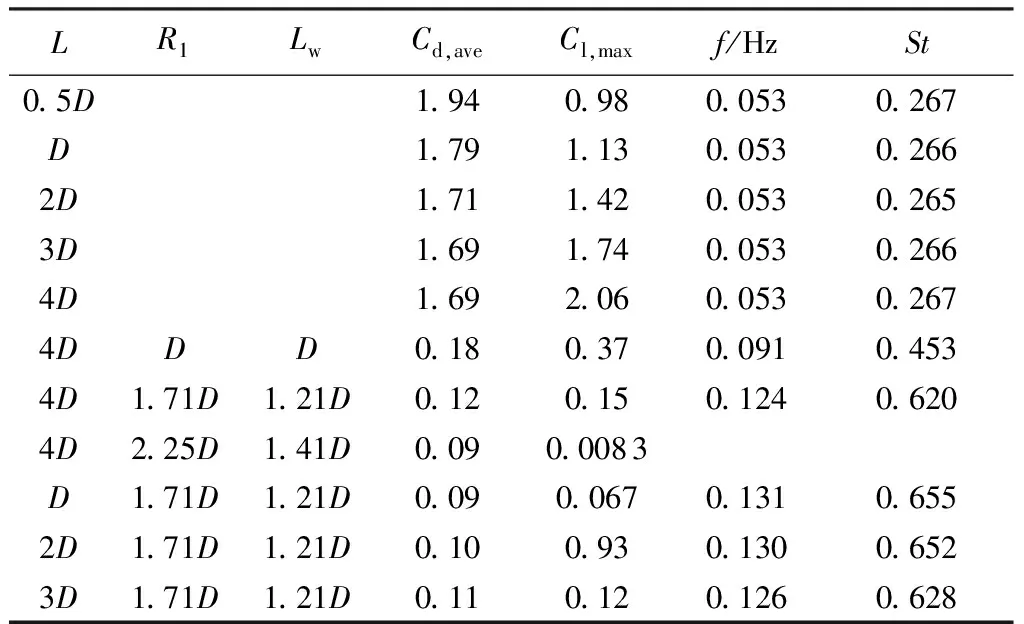
表4 各种闸墩绕流的计算结果

3 结 论

随着流道宽度变窄，圆柱在流道中的占空比增加，圆柱的平均阻力系数、最大升力系数及脱涡的St数都逐渐增大。本文参数范围内的渐变段流道的截面收缩对圆柱绕流的脱涡频率、升阻力均不会产生明显影响。流道的弯曲布局会让流道中的流速分布呈非对称性，偏流系数随截面与弯道距离的增加而增加至稳定值。固定位置截面的偏流程度与上游弯道的转弯半径关系密切，转弯半径越小，偏流系数越大。截面流速分布的偏流系数随转弯角度增加也有所增加，但超过60°以后，角度增加对流动偏流程度的影响不大。弯道导致的偏流效应使得圆柱脱涡和受到的升阻力都不再对称。偏流系数增加，圆柱的升阻力系数峰值差异、升力系数平均值都有所增加。无墩尾闸墩绕流的流场和受力均与圆柱绕流类似，平均阻力系数随墩体长度增加略有降低。带墩尾的闸墩呈流线型，相比于无墩尾闸墩，其升阻力系数都明显减小。因此闸墩设计安装合适的墩尾是改变绕流流态、消除旋涡的有效措施。