有效的情境 充分的活动——听荷兰专家米歇尔博士上课有感

◇陈 敏

在第三届中荷现实数学教育高峰论坛暨第八届中国小学数学教育峰会上， 荷兰专家米歇尔·维尔德休斯（Michiel Veldhuis）博士现场教学了一节三年级的代数启蒙课，以具体、直观的方式解读了现实数学教育（RME）的相关理念，且使参会者深切感受到中荷数学课堂教学的差异。

这节课是由荷兰资深现实数学教育专家马尔嘉（Marja Vanden Heuvel-Panhuizen）教授领衔的研究团队（米歇尔博士是其中的主要研究人员）开发的早期代数系列课之一。据介绍，这一系列的代数课共有6 节，教学的重点是有关线性方程的代数推理，此为第一节课，经过逐步形式化，至第6 节课达到能求解简单二元一次方程组的目标。

一 从教师引导学习到情境激活学习

一上课，米歇尔博士先邀请孩子们观察课桌上的新学具——“挂摆（hanging-mobile）”。（如图1）

图1

师：你们一定看见了这里有一些奇怪的东西夹在桌子上，你们知道这是干什么用的吗？

生1：这是上课要用的吧？

师：对，非常准确的回答。那你们觉得这节课会做什么呢？

生1：我感觉要教数量相等这样的内容。

生2：我觉得像一个秤。

生3：我觉得不是秤，因为秤上面都标有数字 1、2、3、4、5……这个上面没有标任何数字。

师：你们说得都很有道理。这是一个比较奇怪的秤，确实没有标刻度。现在我来告诉大家，我们叫它挂摆：它上面是可以挂东西的，摇摇摆摆的外形很像小宝宝床头悬挂的玩具，这就是为什么我们叫它挂摆。

然后，围绕“挂摆”, 米歇尔博士先后布置了3 个学习任务。

⋆小组任务1：只看不动，想象如何操作能够保证挂摆保持水平，画在海报纸上。

（注：每个小组的挂摆均呈水平状态，其所挂小球却不尽相同，比如组1 的情况是1 红+1 黄=1 黄+2 白，如图 2；组 2 的情况是 1 红+1 黑=1 黑+3 蓝， 如图3……不同颜色的球大小相仿，质量不同，但小球上没有表示质量的数字符号）

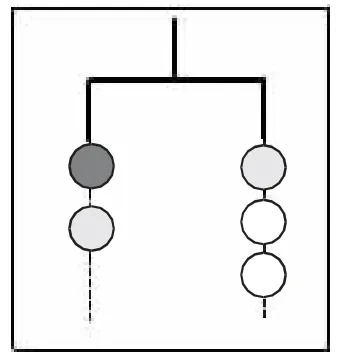
图2

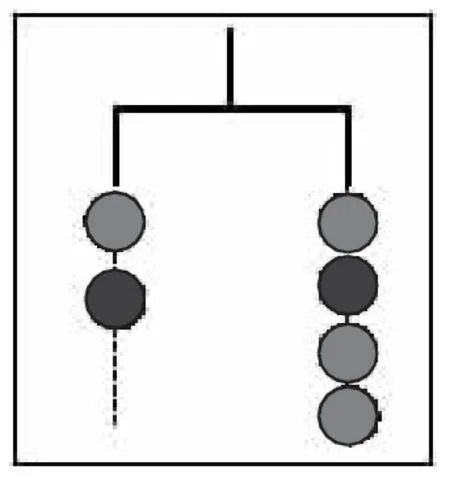
图3

⋆小组任务2：动手操作，尝试进行哪些操作可以使挂摆保持水平。 然后修改并丰富小组海报。

⋆小组任务3：请从抽屉中取出更多小球，尝试进行哪些操作可以使挂摆仍保持水平。然后画在海报上。

最后，教师组织集体交流，小结保持挂摆平衡的主要方法（实质为等式的有关性质）。

统计发现，小组活动期间教师和个别小组之间的谈话共计39 次，其中由学生发起的谈话29次，内容多为询问活动规则或分享结论，如“我们可以用自己的笔来画海报吗”“如果写错了，可以重来吗”“我们发现了1 个红球等于2 个白球”等。由教师主动发起的谈话10 次，内容多为督促学生参与或了解学生想法，如“你试过操作挂摆了吗？所有的方法都试了吗”“我看见你们把小球都从链条上方取到了链条下方， 你们是怎么想的”等。

最后的集体交流过程中教师发言约19 次，属于有意讲授或提问某个知识点的仅3 次，例如：我可以把上面这个球拿下来放到下面吗？（指挂摆同一侧的球相互交换位置）我可以把两边交换位置吗？挂摆还是平的吗？其余多为对学生发言的肯定，对汇报活动的组织等，如：你们还记得我们要研究的问题是什么吗？你可以上前来操作一下看看是不是真的还平衡。（如图4）

图4

显然，在这节课上，学生的学习非常自主。他们不是根据教师的言语线索学习，而是直接和情境对话——由“挂摆”系列情境问题引导他们感知“相等”的概念、体会等式的有关性质。这也可以从三次小组活动期间学生主动发言的内容指向上得到体现：学生越来越少关注教师的意愿，而越来越多地投入任务本身。（如表1）

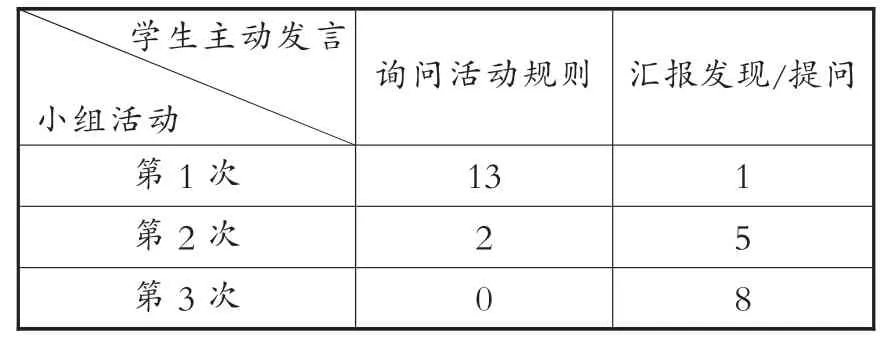
表1 学生主动发言内容指向统计表

本课中， 米歇尔博士向我们展示了另外一种教学形态，即教师对学生的引导作用更多体现在课前对教学情境的预想和设计中，而在课堂内较少直接地讲授和“小步子”提问。在课堂上，教师主要是观察者与合作者——观察和评估学生的表现水平，相应地调整教学进度，并给予助力服务。马尔嘉教授在她的专题报告《现实数学教育遇见中国数学教育》中提到，RME 的“R”即“Realistic（现实的、恰如其分的、逼真的）”，强调教师要提供给学生适切的问题情境（并非专指现实生活情境），通过情境去帮助学生产生与数学相关的、有意义的想法。

二 特别重视学生活动经验的积累

RME 认为，学生对数学内容的认识和理解总是从他们自己日常的、非正式的推理开始的［1］。米歇尔博士在课前还作了主题为《在小学数学教学中培养高阶思维》的专题报告，对培养高阶思维的学习促进因素作了理论分析，其中特别提到“具身认知理论（Embodied cognition）”和“表征重述理论（Representational redescription theory）”。前者强调活动性原则，即“学生的感觉运动系统在概念理解的发展中发挥着重要作用（Gallese &Lakoff,2005）”； 后者认为人的认识具有层次性，“那些初始的、隐含的、具体化的知识会进入使用语言或其他符号重述表征的下一阶段，进而参与明确的语言-符号推理和明确的由假设指导下的实验（Karmiloff-Smith,1992）”。

因此，这节课作为一节启蒙课，学生的操作活动特别充分，不仅时间宽裕（全课用时约55 分钟，其中学生操作时间约30 分钟），而且自主支配空间也很大。 米歇尔除了提醒孩子们不要拉、拽挂摆，以免砸到自己，以及组员之间要相互倾听、协作，鼓励孩子们用各种方法去操控挂摆，观察平衡的实现。 他有时会主动询问：“你们在研究什么？”“这是真的吗？你们可以操作给我看吗？”但他没有给出答案或者进行方法的指导。有时，学生偏离了活动主题，比如有一个小组兴奋地告诉米歇尔，他们已经测试出哪个球最重，正在找寻第二重的球，米歇尔也没有阻止他们。笔者认为，教师的行为可以被理解为：一方面，他对挂摆的情境足够自信——自信挂摆会引导学生得出有益、有效的结论；另一方面，也可以看出这节课的教学目标仅止于非正式地、预形式化地体会等式性质，所以只要是操作挂摆，体会挂摆的工作原理，都被教师认可为必要的探索过程，都有耐心去分享和等待。

基于充分的活动， 最后师生总结出了保持挂摆平衡的常用方法，即，挂摆两边同时添上或取走相同数量的同色小球，挂摆两边同时添上或取走质量相等的小球（如1 个红球对应2 个白球），挂摆两边分别反复添上或取走质量相等的小球（如1 个红球=2 个白球→2 个红球=4 个白球），调整同侧小球的高低位置；整体交换挂摆左右两侧的小球……涉及了等式性质的方方面面。 随着数学活动经验的累积，学生确实具备了进一步形式化和数学化的潜力。

三 进一步的思考

现实数学教育提倡“教师应当与学生处在一种平等关系进行讨论”“鼓励学生积极地独立思考、自主地作出发现”，但“表面上的平等实际赋予了教师更大的责任，对教师能力提出了更高的要求”［2］。当教师要从台前的主导转换为幕后的设计时，其实需要付出更多的智力劳动；同时，课堂上的观察与评估，特别是能基于观察与评估及时作出教学上的调整也绝非易事。我们一线教师要有意识地去培养和锻炼自己在这些方面的专业能力，真正成为课堂学习中的组织者、引导者与合作者。

《义务教育数学课程标准（2011年版）》提出：数学活动经验的积累是提高学生数学素养的重要标志。广大教师普遍认同数学活动经验的重要性，但对小学阶段有哪些重要的数学活动经验、怎样的活动有助于积累数学活动经验、要积累到什么程度等都还没有明确的认识。特别是，我们容易把经验当作手段而非目标（以本课为例，国内课堂可能以挂摆操作20 分钟、等式探究20 分钟这样的结构来教学），而且，由于直接经验的获得需要做大量的准备（包括教学具的设计和制作、场地的预定、学生的组织等），我们常常会用间接经验取代直接经验。这其中的教学效率和效益问题恐怕难以一概而论。