一种新型深潜器耐压壳的非线性屈曲计算

彭 懿，韦乃琨，赵 晶，甄希金，王 浩

(1. 上海船舶工艺研究所，上海 200032；2. 上海申博信息系统工程有限公司，上海 200032)

0 引 言

深海潜水器是在各种复杂海域进行水下科学考察和开发作业的必备装备,是人类研究开发海洋的主要技术之一。耐压壳作为深海潜水器人员和仪器搭载平台，其可靠性、功能性至关重要。耐压壳的可靠性表现为抵抗海水压力的能力，下潜越深需要抵抗海水压力越大。功能性表现为尽可能多地搭载人员和设备，尽可能低的结构重量。李文跃等[1]对大深度载人潜水器的耐压壳结构形式做了较深入的研究，分析了圆柱形、球形、椭球形耐压壳的特点。随着潜深的增加，对耐压壳的抗压能力要求越来越高，张呤等[2]提出了一种新型双层耐压壳结构，研究显示其抗屈曲能力较单层耐压壳有显著提高。随着下潜深度的增加，结构重量与自浮力之间的矛盾将变得更加突出，必须采取有效措施,严格控制结构重量增长幅度，以确保深潜器有效载荷不减少，保持合理的容重比以满足功能需求。张乃樑[3]对比了圆柱、椭球、球球、球柱球3 种形式耐压壳的容重比，得出椭球的容重比最高。圆柱形耐压壳尽管在抗压能力上不及球形和椭球形，但在制造工艺难度、水动力特性、成本、空间利用率等方面有明显的优势，因此本文选择圆柱形耐压壳为研究对象。

由于深潜器耐压壳是受外部水压力，所以屈曲是耐压壳破坏的主要原因。受各种不同力和边界条件约束的圆柱壳屈曲问题，国内外已有大量研究。L.H.Donnell[4]引入缺陷因子的概念讨论了缺陷对轴压薄壁圆柱壳屈曲的影响；Izhak Sheinman[5]给出了几何缺陷纵环加筋圆柱壳在轴压作用下的屈曲数值解；周承倜[6]和陈铁云[7]等研究了具有初始缺陷的环肋圆柱壳在均匀静水压力作用下的弹塑性屈曲；Yamaki[8]系统地研究了受各种不同力和边界条件约束的圆柱壳的弹性屈曲。为了提高抗压能力，控制结构重量，提高容重比，本文参考了王林等[9]的研究，将圆柱形耐压壳设计成纵环加筋圆柱形耐压壳。耐压壳在制造过程中外形难免有缺陷，在学术界将此种缺陷称为初始缺陷，并用初始缺陷挠度来描述。因此问题实质上是有初始缺陷纵环加筋圆柱壳的受压屈曲问题。彭懿[10]对具有初始缺陷的纵环加筋圆柱壳在均匀静水压力作用下的弹性屈曲做了较深入研究，给出了特定条件下的几何非线性解析解。本文在上述研究的基础上，同时考虑几何非线性和材料非线性，用专业计算软件对彭懿[10]的研究做了进一步探讨。

1 非线性屈曲的有限元解法

由于非线性问题的复杂性，往往严格的数学求解是十分困难的，而有限元方法为非线性问题的数值求解提供了有效的工具。有限元方法求解非线性问题是将非线性问题转化为一序列线性问题求解。

目前专业计算软件对结构进行非线性屈曲计算是通过非线性静力分析实现的。利用线性加载方法逐步施加载荷，直至结构的切向刚度矩阵变成奇异阵，可以认为结构此时屈曲，即可终止计算，并认为此时的载荷即为屈曲临界载荷。

为了帮助理解非线性屈曲的有限元计算，下面简单介绍基本思想[11]。

非线性计算，不能直接由线性方程组求得响应，需要将载荷分割成若干增量求解，每一增量内将非线性变量线性化，然后由线性方程组求得这一增量内的响应。但纯增量法没有考虑由线性化导致的误差，前一增量步的误差会累积到后一步，误差的累积会使解明显偏移。

与线性问题不同，无论是材料非线性还是几何非线性，单元刚度矩阵 [ke] 与单元节点位移 {d}e相关。假设结构体的刚度矩阵 [K{d}] ，节点位移为 {d}，外力为{R}，非线性有限元方程为：

式（1）可以写成下面的形式：

则方程 {f{d}}=0的根即是式（1）的解。式（2）中[K{d}]{d} 是 内 力， {R} 是 外 力， {f{d}}是 内 力 与 外 力的不平衡力，只有 {d} 为精确值时 {f{d}}=0才成立。求解式（2）一般都采用线性化方法，把非线性问题转化为一系列线性问题求解。即把整个载荷分为若干个子步（增量）加载，每个子步内都进行线性迭代运算。具体做法是在每个子步内用切向刚度矩阵 [KT]代替刚度矩阵 [K{d}]，这样非线性方程式（2）就变为如下线性方程：

式中切向刚度矩阵 [KT]可根据应力应变曲线求得。

显 然 将 变量 [K{d}]用 常量 [KT]代 替 会产生误差，导致{f{d}}≠0。为了消除误差需要通过迭代运算，通常使用的迭代算法有Newton-Raphson 法和Risk 法。高良田等[12]采用Risk 法对球形耐压壳的非线性屈曲做了计算，取得较好的结果。Risk 法被认为是目前结构非线性屈曲计算中数值计算最稳定、收敛性最好的迭代计算方法之一，本文采用Risk 法计算耐压壳的非线性屈曲。

2 计算模型创建

2.1 物理模型简介

物理模型数据来自于王林等所做的实验[9]，本文只将纵筋的位置调整为内加筋，使模型的结构形式与耐压壳的结构形式一致。模型为纵环加筋圆柱壳，模型两端用厚钢制法兰密封固定。壳体半径R=850 mm，壳体长度L=500 mm，壳体厚度t=4 mm；肋骨共有11 根，间距l =46 mm，肋骨尺寸： S1=δ ×h =6 mm×21 mm=126 mm2， δ为环筋的厚度， h为环筋的高度；纵筋位于圆柱壳内侧，共24 根，沿圆周均布，间距b=222.5 mm，纵 筋 尺 寸： S2=δ ×h =4 mm ×15 mm=60 mm2， δ为纵筋的厚度， h为纵筋的高度；壳体、环筋、纵筋是同样的材料。材料屈服极限是 σs=784 MPa，材料的弹性模量是 E =2.0 ×105MPa，材料的泊松比是 µ=0.3。

2.2 单元选取与材料模型

圆柱壳体使用壳单元，法兰采用壳单元，纵向和横向加强筋均采用梁单元。

由于王林等所做的实验[9]中只给出了材料常数，没有给出材料的应力应变曲线。在此假定材料为理想弹塑性且各向同性硬化材料，材料应力应变曲线采用双线形。材料应力应变曲线如图1 所示。

图1 材料应力应变曲线Fig. 1 Material stress-strain curve

2.3 有限元模型

整个模型划分为3726 个单元。法兰用三角形网格自由划分为678 个壳单元，圆柱面用四边形网格划分为1 440 个壳单元，纵向和横向加筋共划分为1 608 个梁单元，如图2 所示。

图2 非线性屈曲计算有限元模型Fig. 2 FEM for nonlinear buckling calculation

2.4 载荷和边界条件

如图3 所示，耐压壳内部被刚度远大于耐压壳的舱壁分隔，因此可以认为耐压壳的端面是被刚性固定的。耐压壳外部加静水压力，加载方式采用分步加载，直至耐压壳发生屈曲破环，载荷的上界取线性屈曲分析的结果6.61 MPa[10]。

2.5 初始缺陷引入

图3 非线性屈曲计算的载荷和边界条件Fig. 3 Load and boundary conditions for nonlinear buckling calculation

在耐压壳或实验模型实际的加工、装配、焊接过程中，产生变形是不可避免的，这使结构偏离正确的形状，产生所谓的非圆度。在学术界将这种非圆度称为初始缺陷。无论是实际使用的深潜器还是用于实验的模型，由于加工工艺的限制，都无法避免初始缺陷的存在。初始缺陷对屈曲的影响也发表了大量研究结果[4-7]。研究结论表明初始缺陷对耐压壳的屈曲有明显影响，显著降低了耐压壳的临界屈曲载荷。因此，在耐压壳的屈曲计算中必须考虑初始缺陷。张菊等[13]对耐压壳初始缺陷的检验方法、检测原理、偏差计算做了探讨，但对耐压壳的初始缺陷的精确数学描述是很困难的。为此国内外研究者[14]在研究耐压壳的非线性屈曲时的一致做法是将1 阶模态通过适当变换作为初始缺陷。本文也使用此方法。初始缺陷引入分为2 步：第1 步进行线性屈曲计算，得到1 阶模态（见图4）并将1 阶模态的节点位移导出；第2 步将节点位移做适当变换引入有限元模型得到具有初始缺陷的有限元模型。至此就得到用于非线性屈曲计算的有限元模型。

图4 一阶屈曲模态节点位移图Fig. 4 Displacements of nodes under first order buckling mode

3 计算结果

将节点位移做适当变换引入有限元模型，分析了初挠度幅值分别为：0.8 mm，1.0 mm，1.5 mm，2.0 mm的纵横加筋圆柱壳的非线性屈曲临界载荷。分析结果如图5～图8 所示，并将各初挠度下的临界载荷用表1列出。图5～图8 中的纵横加筋圆柱壳轴向半波数为1，周向整波数为7。这与王林等所做的实验[9]结果一致，说明边界条件和加载方式是合理的。王林等[9]给出基于线弹性理论的完美耐压壳临界载荷解析解是6.56 MPa，实验得出的临界载荷是4.61 MPa，显然基于线弹性理论的解析解要高于实验值。非线性屈曲计算考虑了模型实际存在的缺陷，因此所得的结果小于解析解，而更接近实验值。

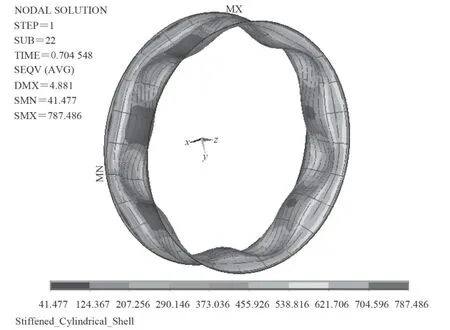
图5 初挠度幅值为0.8 mm 的非线性计算结果Fig. 5 Nonlinear calculation results under initial imperfections amplitude 0.8 mm

图6 初挠度幅值为1.0 mm 的非线性计算结果Fig. 6 Nonlinear calculation results under initial imperfections amplitude 1.0 mm

图7 初挠度幅值为1.5 mm 的非线性计算结果Fig. 7 Nonlinear calculation results under initial imperfections amplitude 1.5 mm

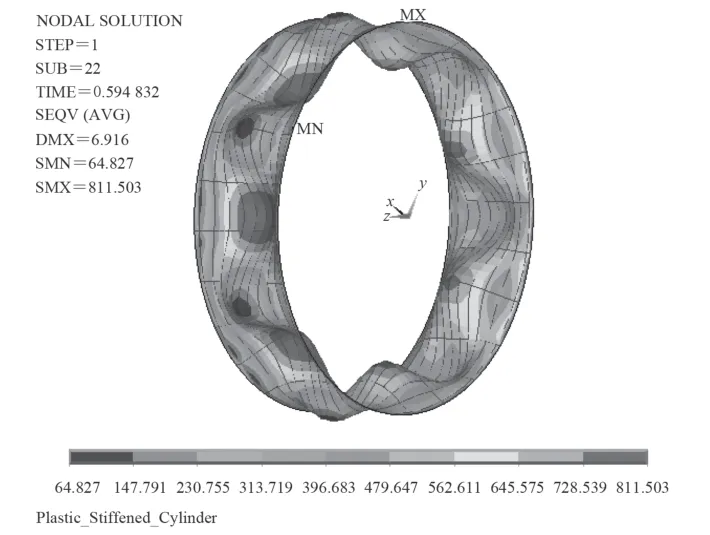
图8 初挠度幅值为2.0 mm 的非线性计算结果Fig. 8 Nonlinear calculation results under initial imperfections amplitude 2.0 mm

表1 不同初挠度下非线性计算所得临界载荷Tab. 1 Critical loads obtained by nonlinear calculation under different initial imperfections

4 结 语

1）Risk 法计算耐压壳的非线性屈曲收敛性好，计算结果与实验值较接近，具有一定的工程价值和指导意义；

2）将耐压壳的1 阶屈曲模态作为初始缺陷波型引入是合理的；

3）外形有初始缺陷的耐压壳临界载荷远小于外形完美的耐压壳，初始缺陷挠度幅值越大，耐压壳的承载能力越差，为了保证耐压壳的安全可靠，必须严格控制加工工艺误差；

4）本文采用的材料应力应变曲线是理想化的，与真实曲线存在差异，这种差异对非线性分析结果有影响。为了使计算更加准确，有必要通过材料力学实验得到准确的应力应变曲线。