砰击载荷下三维变形结构动态响应的数值模拟

王加夏，陈 月，彭丹丹，刘 昆

(江苏科技大学 船舶与海洋工程学院，江苏 镇江 212003)

0 引 言

砰击现象广泛存在于在汹涌的海面上航行的船舶与海洋结构物中，例如小型的高速艇，大型的商船和豪华邮轮等。当砰击发生时，结构物在短时间内受到较大的冲击力，这种冲击力有可能会破坏结构甚至造成人员的伤亡。因此，在船舶设计中，准确预报结构物砰击载荷对结构设计至关重要。

砰击问题的研究最早是由Von Karman[1]开展的，他将水上飞机的降落过程简化为二维楔形体砰击水面的理论模型。随后，Wagner[2]在Von Karman 的基础上，考虑了结构冲击时的液面抬升现象，并且引入了湿表面的概念。Dobrovol'skaya[3]将二维刚性楔形体等速入水的势流问题转化为复平面内的自相似流问题，求解了整个流场的流体速度和压力。Zhao 等[4]采用完全非线性边界元法研究斜升角为4°～81°二维结构的入水问题，采用非线性物面条件、自由液面条件进行计算。Muzafrija 等[5]使用有限体积法（FVM）和VOF（Volume of Fluid）类型的自由表面建立模型，这种方法通过精细的网格能很好地捕捉射流的发展，结合自由表面捕获模型，预测了结构入水的粘性自由表面流。在试验研究方面，Stavovy[6]通过刚性平底结构及斜升角为1°～15°的刚性楔形体模型的入水冲击试验，得到了最大砰击压力与斜升角之间的关系。Ochi[7]总结上百个船模在波浪中的砰击试验数据，提出了船舶剖面底部的砰击压力公式。近年来，有限单元法（FEM）广泛应用于流固耦合问题中。Peseux[8]应用有限元法和实验方法研究了三维刚体和弹性结构的砰击问题，结果表明刚体试验的规律性较好，而弹性体结构的结果有待进一步解释。赵九龙等[9]基于三维边界元方法和Wagner 自由液面抬升理论，建立“等效自由液面”的新数值计算方法。

当不考虑结构变形时，流场演化特性以及结构砰击载荷的相互作用已经通过数值模型进行了广泛研究。然而在实际应用中，流场砰击载荷和结构砰击响应的过程是相互耦合、相互影响的，是由流场演化和结构响应特征共同决定的，因此需要建立计及结构变形效应的精确砰击数值模型。本文利用STAR-CCM+（STAR）和Abaqus 软件进行外部耦合，建立了考虑结构变形效应的砰击数值模型，并研究三维楔形体结构入水砰击时弹性效应对砰击压力和结构动态响应的影响，观察不同入水阶段，结构变形模式的变化，并考虑板厚变化对楔形体结构响应的影响。

1 数值模型

1.1 流体控制方程

STAR 软件基于FVM 法将连续控制方程转化为可以求解的代数方程组，使用VOF 多相流模型追踪自由液面的形态变化。对于粘性的三维流动，假定流动由RANS 方程控制，其中湍流效应包括涡度粘性模型。在这种情况下，求解连续性方程、动量方程和2 个湍流特性方程。首先空间域被细分为有限数量的邻接控制量（CVs），并且当CVs 随着结构运动而移动时，必须注意空间守恒定律。控制方程如下[10]：

质量守恒

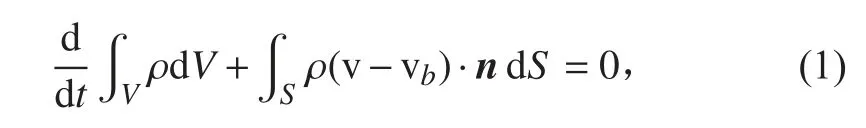
动量守恒

标量形式的一般输运方程

空间守恒定律

其中：ρ 为流体速度；v 为流体速度矢量；vb为CV 表面的速度；n 为表面为S 体积为V 的CV 表面的单位向量法线；T 为指应力张量（用速度梯度和涡粘性表示）；p 为压力；I 为单位张量；φ 指代标量（k，ε 或者ω）；Γ 为扩散系数；b 为单位质量的体积矢量；bφ为φ 的源和汇方向。

1.2 结构响应方程

在Abaqus 中计算水动力载荷下结构变形时，需求解瞬态动力学方程[11]：

式中：M 为质量矩阵；Mh为附加质量矩阵；K 为刚度矩阵；D 为阻尼矩阵，由M 和K 决定；Dh为附加阻尼矩阵；Fce为旋转所产生的离心力；Fco为惯性力，当小变形时可忽略不计；Fh为水动力载荷；u 为位移。

1.3 流固耦合

结构入水砰击问题属于强非线性的流固耦合问题，本文通过协同耦合功能自动在流固交界面处进行数据的交互传递实现双向的流固耦合计算。其中STAR 求解流体方程，Abaqus 求解结构方程，属于分区式流固耦合FSI（Fluid-structure interaction）。本文主要采用隐式耦合算法，并在每个外迭代计算流场载荷及更新结构物的受力、位移及变形。

根据流固耦合所遵循的守恒原则，在流固耦合交界面上，流体域和固体域之间相互传递的应力σ 与位移d 等变量应当是守恒的，即

式中：下标f 表示描述流体域的变量；下标s 表示描述固体域的变量。流固耦合中流体求解和固体求解的方程及数据交换如图1 所示。

在STAR 中设置运动规范为“变形”，在Abaqus

图1 流固耦合方程及数据交换示意图Fig. 1 Sketch map of fluid-structure coupling equation and data switching

图2 流体流动与流动诱导的结构响应求解流程图Fig. 2 Flow chart of a coupled simulation of fluid flow and flow induced motion in a floating body

设置模型的弹性模量、板厚、初始速度、重力、时间步长和耦合面等参量。具体计算流程如下：首先STAR 开始流场载荷计算，然后将压力和剪切力传递给FEM 求解器，之后Abaqus 根据耦合界面的载荷进行结构响应分析并将得到位移和变形量传递给STAR，STAR 再根据传递的位移量通过“变形”功能实现网格的移动，这样完成一次协同耦合进行计算更新，重复直至达到最大物理时间。

2 计算模型及模型设置

本文以30°倾角的楔形体为例，建立变形楔形体入水砰击的数值模型，并和模型试验相对比，验证了数值模型的有效性。同时增加板厚使得结构偏于刚性，研究楔形体入水砰击时变形效应的影响规律，研究砰击载荷时空分布、结构响应规律等特性，分析得到在砰击现象这一强流固耦合问题中不同板厚时结构变形的影响规律。

2.1 计算模型

由于结构在入水砰击过程中，涉及到结构-液体-气体等三相物质，同时还需进一步追踪结构和自由液面大位移的运动，结构的变形使得每一时间步需要对网格进行重构，增加了计算的复杂度。为解决此问题，本文引入三维重叠网格技术（overset mesh），该技术可考虑结构大变形，适合求解该类复杂的流固耦合问题且无需网格重构。另外，固液交界面会出现流场射流现象，为清晰捕捉射流的演化形态，本文在交界面处采用网格细化技术得到精细网格。

整体计算背景区域为0.8 m×0.8 m×0.8 m，重叠网格区域为0.4 m×0.7 m×0.35 m。坐标系原点在楔形体底部中点处，z 轴竖直向上为正，x 轴水平向右为正，右手螺旋法则，其中水面在z=-0.01 m 处。计算域在Y=0 处剖面如图3 所示，楔形体尺寸如图4 所示。

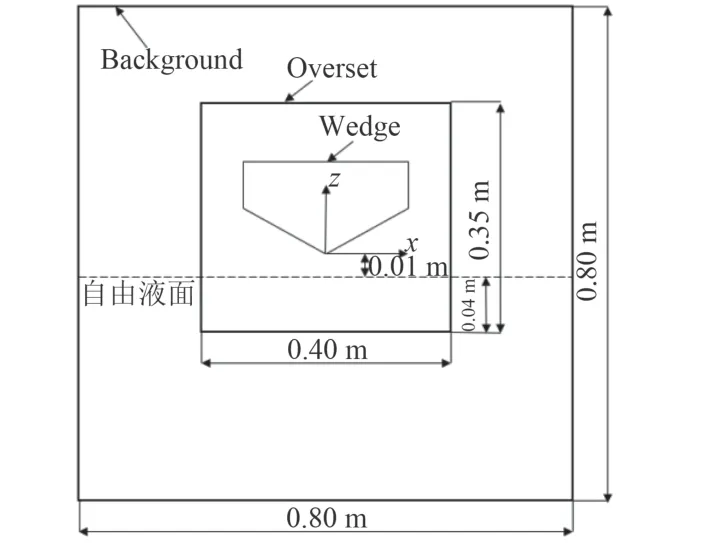
图3 Y=0 处计算域剖面Fig. 3 Computational domain profile in Y=0

图4 楔形体模型尺寸Fig. 4 Size of the wedge model

计算区域内部采用表面重构、自动表面修复、切割体网格单元、棱柱层网格的方法进行网格的生成，为了在最大程度上消除在2 个网格间插入变量时产生的错误，对背景网格和重叠网格的重叠区域使用相同的网格密度数量级。背景区域除顶部采用压力出口条件，其余都采用壁面边界条件，重叠区域中楔形体采用壁面边界条件，其余采用重叠网格边界条件。计算区域的网格划分具体如图5 所示。

2.2 测点分布

通过在底板不同高度位置处布置测点对结构入水时压力时间变化进行监测，考虑到楔形体的对称性，只在一侧取点。测点布置如图6 所示。底板中心为O 点，在底板一侧的横向中心线距离O 点15 mm 处布置测点P1，之后每隔30 mm 布置1 个测点，即P2，P3，P4，P5。

2.3 模型验证

图5 计算区域网格划分Fig. 5 Computational domain mesh

图6 楔形体底部测点布置图Fig. 6 Point layout at the bottom of the wedge

为了验证本文所建立的考虑结构变形效应的流固耦合数值模型的有效性，通过STAR 与Abaqus 进行耦合对弹性楔形体入水砰击过程进行仿真模拟，并和模型试验[12]进行对比，试验中模型的板厚为5 mm，从0.4 m 的高度自由下落，模型尺寸见图4。图7 给出了P3，P4测点压力曲线的实验值和数值仿真结果对比，楔形体在接触水面的瞬间，砰击压力迅速达到峰值，随着时间的推移，各测点出现峰值后迅速减小至趋于稳定，测点P3的峰值要大于测点P4。由图可知，两者曲线吻合良好，弹性仿真的最大峰值相比试验测量值稍小，可以认为弹性体入水耦合仿真的结果是可靠的。

3 计算结果分析

板厚的变化会影响结构弹性，为了研究厚度参数对弹性结构响应的影响，本文针对不同板厚的楔形体进行了计算，通过对比结构的砰击压力、变形位移和应力分布等参量来分析结构弹性变化对结构动态响应的影响。

图7 测点实验值和数值仿真结果对比Fig. 7 Comparison of experimental and numerical simulation results

为分析板厚对楔形体入水动态响应的影响，改变斜升角30°楔形体的板厚，定义板厚分别为2 mm，5 mm，8 mm，12 mm，设定楔形体以10 m/s 的速度冲击水面。不同板厚时P1～P4测点砰击压力曲线如图8所示。由图可知，楔形体在接触水面的瞬间，砰击压力迅速达到峰值，随着时间的推移，各测点相继出现明显的峰值后迅速减小，板厚越大砰击压力越大。另外，从图中圆圈处可以清晰地看出，在0.008 s 之后，当板厚减小时，砰击压力曲线出现了明显的波动，板厚为12 mm 时曲线较为平稳，板厚5 mm和8 mm 时曲线有微小波动，板厚2 mm 时曲线波动较大甚至出现负压，这是由于板厚的变化造成结构弹性特征改变引起的，板厚越小，结构弹性越大，流固耦合时弹性效应的影响越大，因此结构的变形越大，同时变形引起的压力波动越大。

图9 给出了弹性模量（E=2.1E11 Pa）和入水速度（v=10 m/s）保持不变时，板厚依次增加，楔形体的最大压力峰值对比图。由图可知，随着板厚的增加，楔形体的最大压力极值是逐渐增大的。这是因为板厚越大使得结构刚性越大，质量越大，砰击压力极值越高。这也从侧面表明了在结构入水砰击响应计算中，为准确预报砰击载荷，需要采用流固耦合的数值模型并计及结构变形效应的影响。

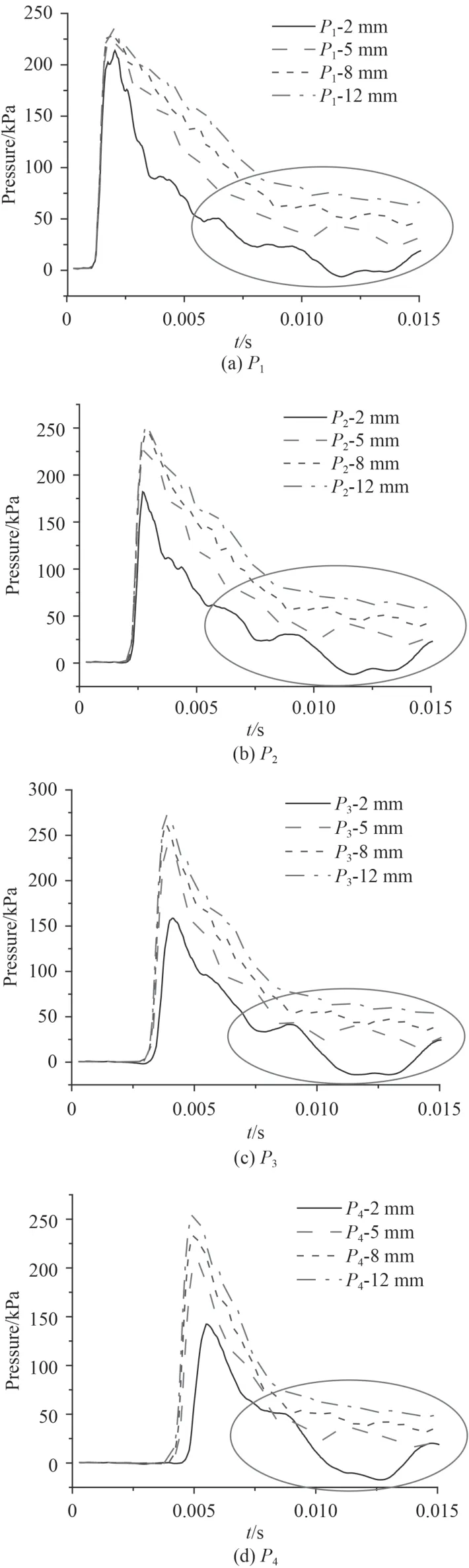
图8 不同板厚各测点砰击压力曲线对比Fig. 8 Comparison of slamming pressure of each point with different thickness of plate

图9 不同板厚时楔形体最大砰击压力峰值对比Fig. 9 Comparison of maximum slamming pressure peak values of wedges under different thickness of plates

图10 不同板厚时各测点变形位移Fig. 10 Deformation displacement of each measuring point at different plate thickness

图10 为不同板厚的楔形体测点P1-P5的变形位移曲线。可以看出，不同板厚的各测点位移曲线总体趋势均为随时间的增大而增大，但当板厚较小时（图10（a）），各测点的变形幅度和变形模式有所差别，测点P1与其他测点的位移响应具有反相位特性；而在板厚较大时（图10（b）），各测点的位移值非常相近，位移曲线几乎重合。这是由于板厚改变了结构的刚度，板厚越厚，结构刚性越大，结构各位置变形幅度越一致。另外，在0.008 s 之前，即楔形体完全入水前，位移曲线斜率要大于完全入水后，这是由于完全入水前结构砰击压力很大，结构变形速度相对较大，而完全入水之后结构受力迅速降低，因此变形位移增加趋势减缓。

图11 不同板厚P1，P4 测点变形位移对比Fig. 11 Comparison of deformation displacement of P1 points and P4 points with different thickness of plate

图11 为楔形体在不同板厚时P1，P4测点的变形位移对比。由图可知，不同板厚时各测点的位移曲线均为随时间的增大而增大；板厚12 mm 时，位移近似一条直线，而板厚2 mm 时，位移近似一条曲线，显示出较为复杂的变形位移。这是因为板厚越厚，结构的刚度越大，结构越不易发生变形。

图12 给出了楔形体板厚5 mm 时不同时刻的各方向应力云图，从图12（a）中可以看出，当楔形体刚接触水面时，最大应力集中在楔形体底部尖端处；从图12（b）、图12（c）可以看出，在入水过程中，应力集中开始由底部尖端处向上转移，最终出现在楔形体顶板中心；从图12（d）可以看出，在楔形体完全入水后，楔形体的整体应力迅速降低，这与图8 中0.008 s之后砰击压力迅速降低相符；从图12（e）中可以看出，当楔形体完全入水一段时间后压力稳定时最大应力出现在楔形体底部尖端处，且顶板中心由于受挤压也存在大的应力集中现象。

4 结 语

本文通过基于VOF 和FEM 方法的流固耦合数值模型，对三维弹性楔形体进行入水仿真，对比分析了结构弹性变形对砰击压力、结构动态响应和结构应力分布的影响。

1）通过STAR 与Abaqus 耦合对弹性楔形体的入水模拟得到的砰击压力值与实验值吻合较好，验证了本文建立的数值分析模型的有效性。

2）研究了结构在不同板厚情况下入水砰击时结构变形效应的影响规律。结果表明：结构板厚越小，结构弹性效应对流固耦合的影响越大，结构所受砰击压力越小且压力波动越大，同时变形位移增大且变形模式较为复杂。表明了结构设计过程中，计及结构变形效应的必要性。

3）通过分析结构响应观察到结构在不同入水阶段的应力变化规律为：楔形体完全入水前最大应力由底部尖端处向顶板中心处转移，完全入水后结构整体应力迅速下降，最大应力出现在楔形体底部尖端处，顶板中心由于受挤压也存在大的应力集中现象。

图12 板厚5 mm 的楔形体不同时刻的应力云图Fig. 12 Stress contours for different time of wedge in thickness 5 mm