一类分数阶复混沌系统的异构组合同步
卢 雅,赵小山,徐 涛
(天津职业技术师范大学理学院,天津 300222)
近年来,分数阶混沌系统已经成为一个热点问题,在文献[1]中,作者提出了一种新的混沌同步,称为组合同步,该同步不同于以往的一对一模型,而是扩充到二对一模型,从而实现组合同步。实混沌系统实际是复混沌系统中虚部为零的特例与延拓[2-3],此同步的优点是在传统的一对一模式中,将不能被传送的信号简单地传输出去,具有更高的抗破译性和抗干扰性,增强了保密通信安全性和保密性,因此组合同步成为了学者争相研究的热点。尽管前期的研究已经取得了一定的成果,但主要还是应用在整数阶的混沌系统上,分数阶混沌系统的组合同步需要进行更深入地研究,而分数阶又被学者重点突破到实数范围内,接下来又扩展到复数域上,因此其将会拥有更大的密钥空间,在保密通信中将发挥更大的作用[4]。从复混沌系统发展历程来看,复混沌系统不仅仅局限在适用某一单独学科,在文献[5]中就已说明有许多学者利用复Lorenz 系统来描述失谐激光和液体的热对流现象。复数形式的出现使其在物理界备受重视,但也只是单纯运用到整数阶和实分数阶系统中,在复混沌系统领域研究甚少,且对复混沌系统来说,保密通信中由于复数域的存在,会增加破译的难度。因此,拥有更多的传输信息量,不仅可以提高信息传递的安全性,而且未来还会有更大的研究空间等待学者们的突破。
随着手机、电脑、互联网和大数据等高科技的发展,诞生了黑客这个职业,如“无线万能钥匙”就是一种破解信息传递的黑客软件,因此就要求更多的信息量、更少的研究成本、更快的处理速度和更多种类的数据类型来确保通信的安全性。复混沌系统组合同步的快速发展,可以进一步保护个人、公司、社会的通信安全性与保密性,提升信息安全技术。本文根据主动控制方法让2 个复驱动系统与1 个复响应系统达到组合同步,从而解决3 个系统间的复杂同步问题,提升对未知干扰因素取得提前控制的效果,并通过数值仿真验证该方法对3 个复系统组合同步的有效性与可行性。
1 系统的数学模型与问题描述
1.1 Caputo函数
多种分数阶微分的数学定义中,有3 种是最为常见的[6-13],分别为Grnwald-Letnikov(G-L)函数、Riemann-Liouville(R-L)函数和Caputo 函数,在实际应用中运用较多的为Caputo 函数。
Caputo 函数定义描述如下:
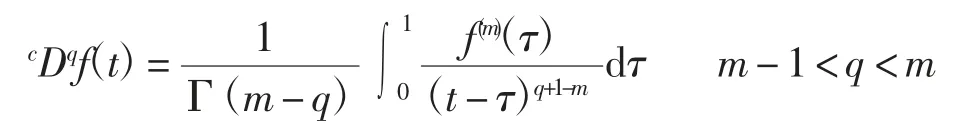
式中:cDq为Caputo 微分算子(0 <q <1);Γ(·)为伽马函数(m 为≥q 的第1 个整数)。
1.2 Laplace变换
Laplace 变换在分数阶微积分理论上占据着重要的角色[14],表达式为:

式中:X(s)=L{x(t)}为x(t)的Laplace 变换;q 为阶数;t 和s 分别为时域和频域的变量。
此外,在分数阶微积分中,经常运用到Mittag-Leffler(M-L)函数,单参数的M-L 函数可表示为:
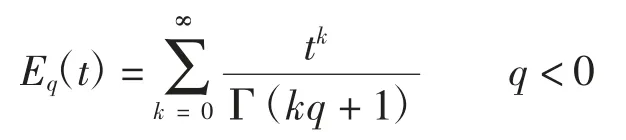
双参数的M-L 函数可表示为:
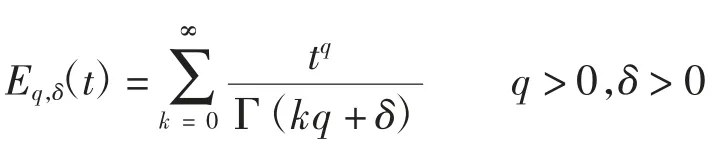
上式Laplace 变换可改写成:
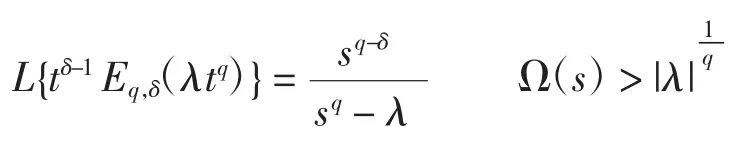
式中:t>0;Ω(s)为s 的实部;λ∈R。
通过计算李雅普诺夫指数来判断系统的混沌现象,研究复系统混沌吸引子的组合同步,通常考虑2个复驱动系统和1 个复响应系统如下:
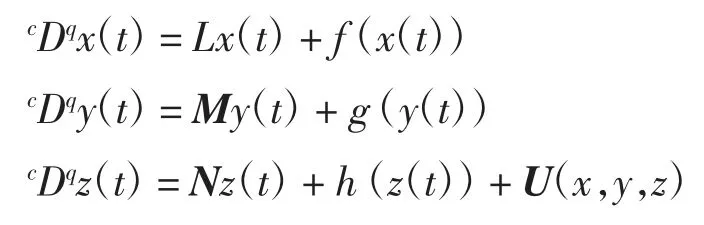
2 分数阶复混沌系统的组合同步方案
定义1对于给定的复驱动系统,复响应系统和任意初始条件x(0),y(0),z(0),2 个常数矩阵A∈Cn×n和B∈Cn×n,如果存在复控制器U(x,y,z),使得在t→∞时,所有的轨道(x(t),y(t),z(t))趋向于流形D={(x(t),y(t),z(t)):z(t)= Ax(t)+ By(t)},即则称复驱动系统和复响应系统达到组合同步。
1.2.2 实施阶段:根据培训计划内容,由带教老师一对一带教,先由带教老师进行操作示范,然后再在工作中练习提高。
式中:A=(s1,s2,…,sn)T,B=(m1,m2,…,mn)T,均为常数矩阵;e=(e1,e2,…,en)T为同步误差;‖·‖为矩阵范数。
为了证明所提出的复混沌组合同步方案的合理性,接下来给出异结构的分数阶复混沌系统之间的组合同步。以复Lorenz 系统为第一驱动系统,用变量x表示;以新的非线性分数阶复混沌系统为第二驱动系统,用y 表示;以复T 系统为响应系统,用z 表示,并说明3 个不同结构的分数阶复混沌系统之间的组合同步的实现。
第一驱动系统为:
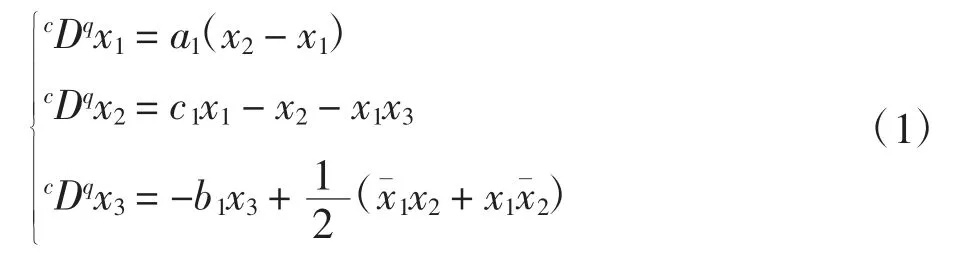
第二驱动系统为:
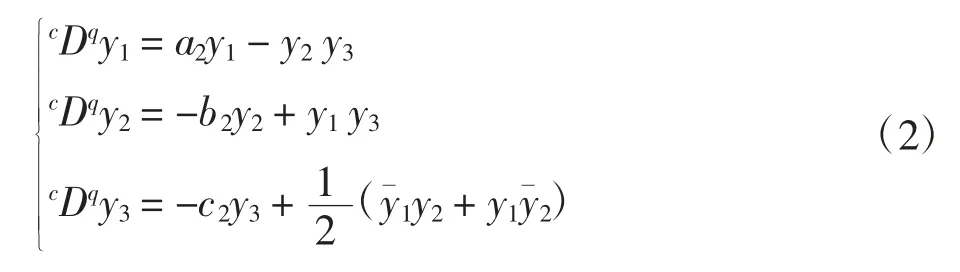
响应系统为:
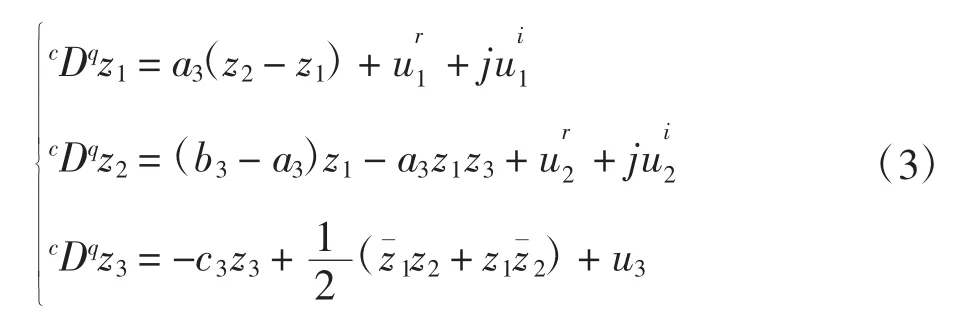
式中:an、bn、cn(n=1,2,3)为实常数系数和z2=均为复变量均为实变量(n=1,2,3)为待设计的实控制器。
设计控制器U 使得2 个驱动系统与1 个响应系统达到组合同步。
引理1[15]若q∈(0,1),x(t)=(x1(t),x2(t),…,xn(t))T∈Rn,其中xn(t)(n =1,2,…,n)是连续可微的函数,则对于任意的t≥0,有:
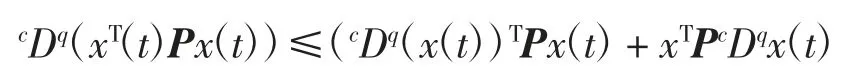
引理2[16]设V(t)是定义在[0,+∞)的连续函数且满足:
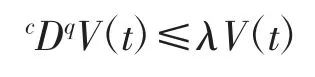
其中λ 为常数,则:
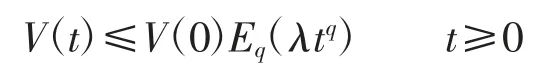
定理1当控制器设计为:
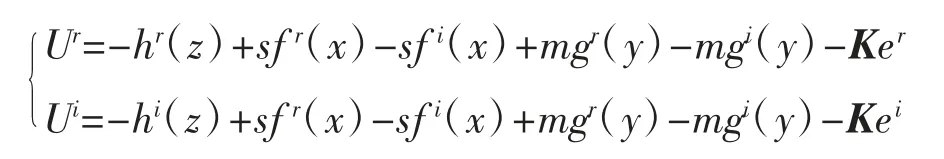
式中:K = diag(k1,k2,…,kn)为实增益矩阵且kn>0(n =1,2,…,n),则复驱动系统和复响应系统实现组合同步。
由定理1 设计如下控制器:
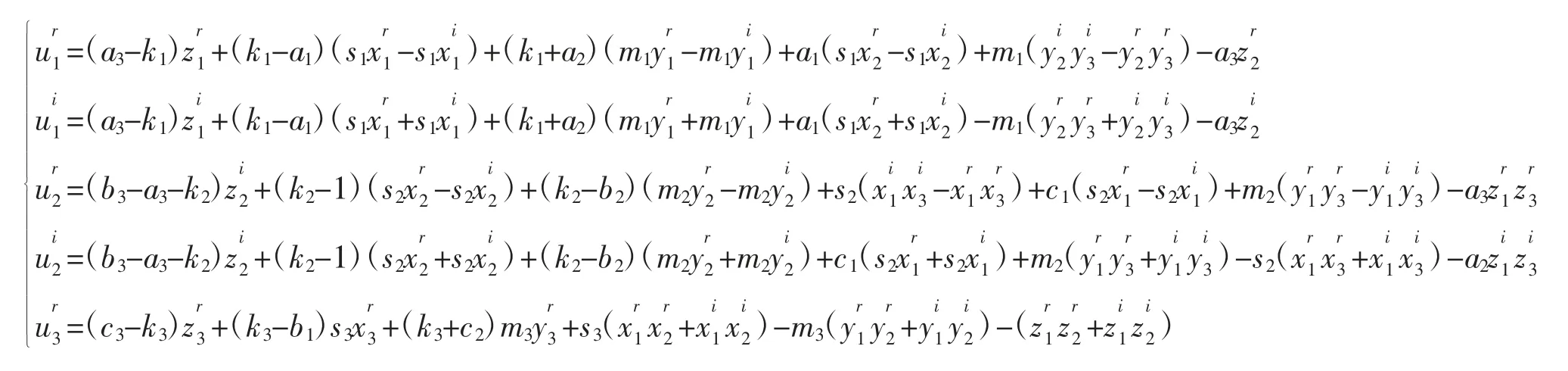
证明由定义可知,系统(1)-(3)之间存在同步误差为e(t)=z(t)-Ax(t)-By(t),借助控制器可以得到如下的误差动力系统:
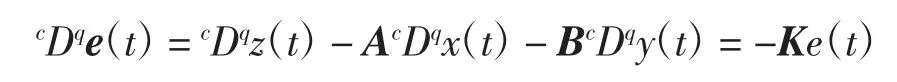
对实部虚部进行分离可得到:
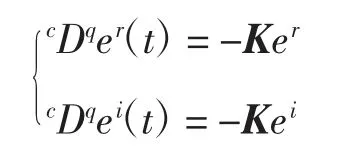
构建正定的李雅普诺夫函数如下:
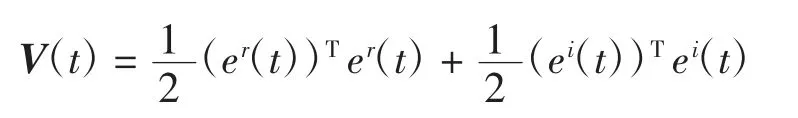
则V(t)=‖e(t)‖2/2,由1.2 中的预备知识可以计算V(t)函数的导数,结合引理1 和方程可得:
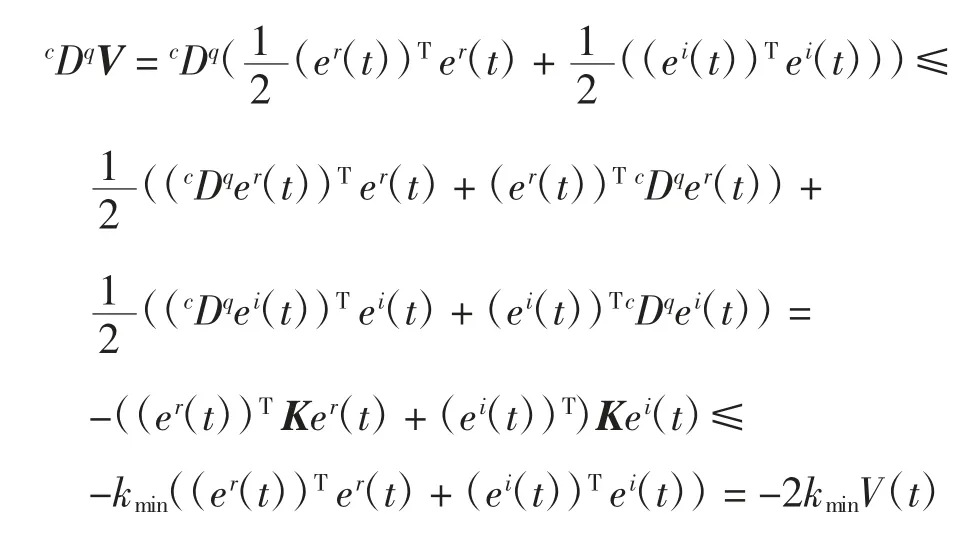
式中:kmin= min{k1,k2,…,kn},由引理2 可得:V(t)≤V(0)Eq(-2kmintq),进一步可以得到:‖e(t)‖2=2V(t)≤2V(0)Eq(-2kmintq)。
若kmin>0,则有因此可以达到驱动系统和响应系统的组合同步,得证。
3 数值仿真
为了验证上述理论的有效性,考虑一个具体的复混沌Lorenz 系统为第一驱动系统,系统阶数为α=0.97,未知参数为a1∈[9,18),b1=1,c1=180 时,此时处于混沌状态并存在混沌吸引子;当a1∈[2,9),b1=1,c1=180 时,也处于混沌现象并存在吸引子,驱动系统(1)的二阶混沌吸引子如图1所示,驱动系统(1)的三阶混沌吸引如图2所示。
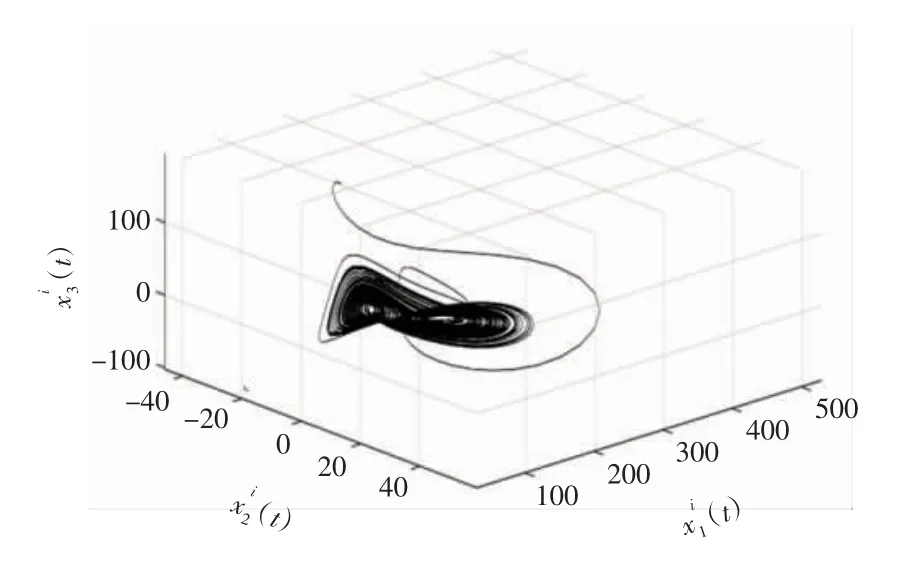
图1 驱动系统(1)的二阶混沌吸引子
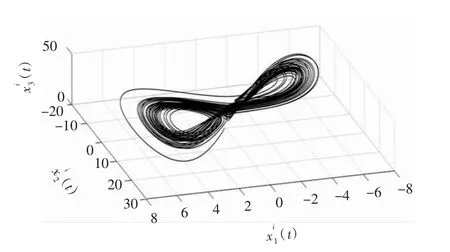
图2 驱动系统(1)的三阶混沌吸引
考虑一个新的非线性分数阶复混沌系统为第二驱动系统,系统阶数取为α=0.97,选取未知参数为a2=9.5,b2=19,c2∈[2,18],存在二阶超混沌吸引子;未知选取参数为a2=9.5,b2=19,c2∈[0,2],存在三阶超混沌吸引子。考虑复T 系统,未知参数取为a3∈[10,13],b3= 0.6,c3= 30,系统阶数为α=0.97,此时存在三阶超混沌吸引子。
利用PECE 法进行数值仿真,选取:A=diag(s1(x),实增益矩阵K 的取值为K=diag(1,1,1)T。驱动系统(1)的初始条件为:
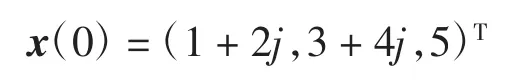
驱动系统(2)的起始条件为:
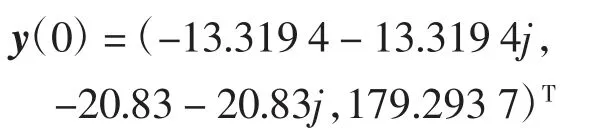
响应系统(3)的初值为:
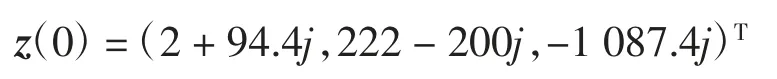
因此,利用数值仿真可以得到同步误差图,误差系统e=(e1,e1,…,en)T分别加入适当的控制器U,得到的时间历程图如图3-7所示。利用主动控制法将2个驱动系统与1 个响应系统实现了组合同步。
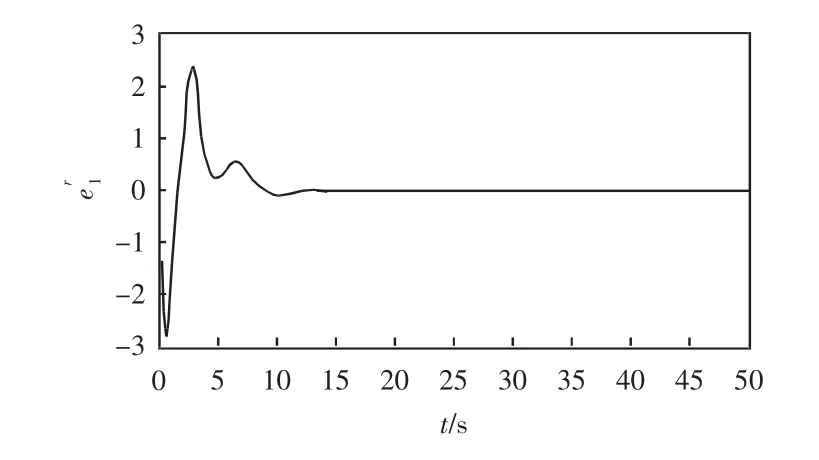
图3 误差系统 加入控制器 后的时间历程图
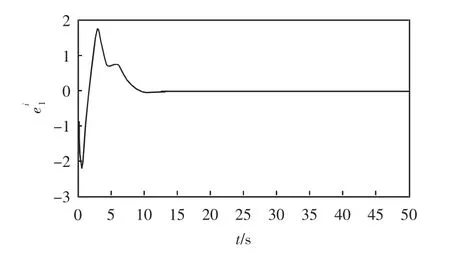
图4 误差系统加入控制器 后的时间历程图
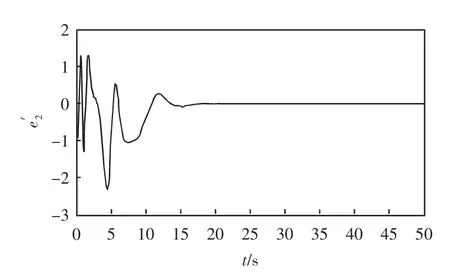
图5 误差系统加入控制器后的时间历程图
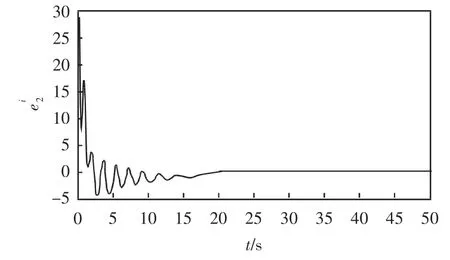
图6 误差系统加入控制器后的时间历程图
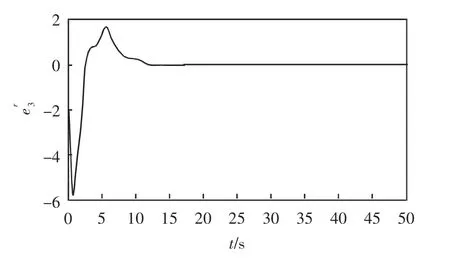
图7 误差系统 加入控制器后的时间历程图
4 结 语
为了研究异构非线性分数阶复混沌系统的同步问题,本文结合主动控制方法,提出了一种组合同步的判据,并以其相应的稳定性理论作为实现异构分数阶复混沌系统的组合同步以及设计相应控制器的理论基础,最终实现了2 个驱动系统与1 个响应系统的组合同步,并分别从理论基础到数值模拟对所设计的控制器的正确性和有效性进行了验证。相对于以往单个驱动系统与响应系统的同步来说,2 个驱动系统和1 个响应系统加大了破译的难度,增强了通信的保密性,为保密通信和密码技术提供了新的思路。

