振荡式喷嘴结构参数对喷雾特性的影响研究

吴永洪 赵文伯 胡宗杰 王宇锋 吴志军

（1.同济大学，上海 201804；2.江苏日盈电子股份有限公司，常州 213000）

主题词：振荡式喷嘴 数值仿真 外流场特性 侧壁张角 喷雾特性

1 前言

射流振荡式喷嘴作为汽车前风窗玻璃清洗系统的核心部件，能够实现射流自激振荡，其低压下射流的喷雾锥角和液滴雾化等性能都有良好表现[1-2]。为了在尽可能不影响驾驶者视线的前提下，及时有效清洗风窗玻璃表面的污渍，确保行车安全，有必要对射流振荡式喷嘴进行深入的研究。

国内外学者对振荡式喷嘴的振荡机理开展了大量研究，结果表明自激振荡是湍流的随机性和附壁效应综合作用的结果[3-6]：Bobusch 等[7]利用粒子图像测速和时间分辨压力测量技术量化分析了振荡式喷嘴内流形态，研究表明，主射流和壁面间漩涡体积循环变化是引起射流振荡的机制；汪志明等[8]通过分析背压及控制流对射流的附壁与切换过程的影响规律得到了射流的附壁与切换原理。随着研究的深入，研究学者发现喷嘴的结构参数对射流振荡影响显著[9-10]：Uzol O等[11]的试验结果表明，振荡室的几何形状，尤其是壁面弧度及其与射流出口截面的距离是影响射流振荡的重要因素；Pandey R J等[12]的数值仿真结果表明，喷嘴腔室入口直径对其内流影响显著，而喉部宽度的影响不明显。同时，射流的宏观特性之间也存在联系：王宇驰等[13]搭建了射流流量计试验研究平台，研究发现，在一定流速范围内，流体流速与内部振荡频率呈现线性关系。

对于振荡式喷嘴的内流特性及振荡机理，相关研究人员已经开展了大量研究，但是关于射流振荡式喷嘴结构对外部喷雾特性影响的研究较少，因此本文基于计算流体力学（Computational Fluid Dynamics，CFD）仿真方法，对振荡式喷嘴内、外流进行同场模拟，研究内流道壁面张角对喷雾特性的影响，为喷嘴的结构设计和优化提供理论依据。

2 喷雾特性测试

本文通过高速纹影成像及自主设计流量收集装置测量获得某款振荡式喷嘴的振荡频率、喷雾锥角和流量分布。高速纹影试验和流量分布测量都需建立喷射压力。低压喷射系统如图1所示，通过调节直流电源输出电流控制水泵，从而实现喷射压力控制。

图1 喷射压力建立模块

2.1 高速纹影成像

高速纹影系统由点光源、光路反射系统、高速摄影仪器、计算机和低压喷射系统组成，如图2所示。

图2 高速纹影试验系统

在侧壁张角θ=25°、喷嘴入口压力为0.2 MPa、出口压力为0 的试验工况下，高速纹影试验结果如图3 所示，在近场区域，喷雾呈现为柱状射流，且射流高频周期性地从一侧摆动至另一侧再回到其初始位置。为减小误差，本文取射流从最右侧摆动至最左侧再回到最右侧为1 个完整周期，根据10 个完整周期的图片张数和拍摄帧速率计算得到平均周期从而获得振荡频率。同时，由图3可测得稳定状态下喷雾锥角为42.4°。

2.2 流量分布测量

流量分布收集系统由流量收集装置和低压喷射系统组成，如图4所示，将收集箱分割为多个收集槽，隔板间隔d=5 mm。通过记录喷射时间和每个收集槽内收集到的水量获取喷雾射流的流量分布数据。图中原点为喷嘴出口对应的收集箱中间的位置，X轴与喷嘴出口截面的长边平行，其坐标值为收集槽中心点与原点间的距离L与间隔宽度d之比。Y轴为垂直喷嘴出口截面方向。

图3 高速纹影成像

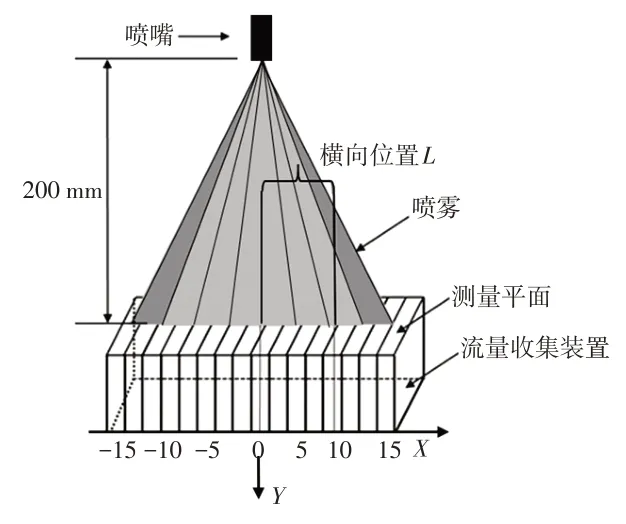
图4 流量收集装置示意

试验工况下，测得距离喷嘴出口200 mm 处X方向的流量分布如图5 所示，整体上呈现为两侧高、中间低的双峰形式。

3 模型建立及验证

本文基于某商用振荡式喷嘴的真实几何模型，建立其内、外流特性数值仿真模型，进行喷嘴内、外流动同场耦合模拟。

3.1 网格划分

图6a 所示为某款振荡式喷嘴的真实三维几何模型。利用布尔运算提取其内流道后对其进行优化，生成图6b所示的内流道几何模型。

因喷嘴入口处结构突变不利于计算收敛，如图7所示，在导出的内流道模型喷嘴入口处增加一段计算域。同时关键细节部位采用0.04 mm的网格尺度，并平滑过渡到其他部位的0.1 mm的网格尺度。

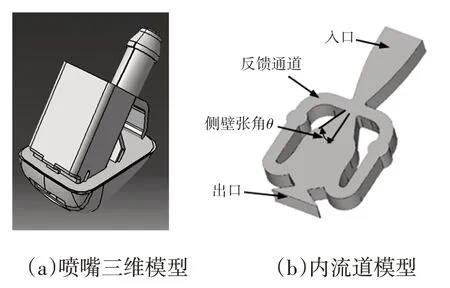
图6 喷嘴几何模型

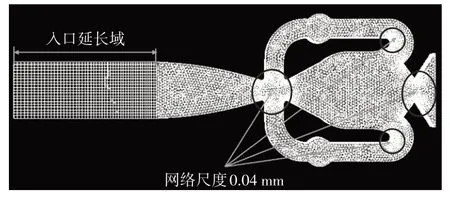
图7 入口区域延长示意

对于外流场，根据试验结果，该喷嘴的喷雾为扇形片状喷雾，锥角为42.4°，覆盖范围为300 mm 左右，喷雾的最大厚度约为40 mm，故设定外流场的尺寸为210 mm×250 mm×80 mm。外流场采用图8a 所示混合网格，即在喷嘴出口处使用非结构网格进行过渡，再拉伸出结构网格。结合喷雾锥角计算将非结构网格区域大小设定为70 mm×50 mm×80 mm，网格尺度由最小的0.1 mm 过渡到最大尺度2.5 mm，网格总数100 万。从计算结果（见图8b）可以看出，混合网格方案能够很好地呈现出喷雾的摆动过程，喷雾云图接近实际喷雾形态。

图8 外流场网格划分方案及计算效果

3.2 参数设置及模型验证

图9所示为计算模型的边界条件，具体仿真参数如表1所示。时间步长的选取对仿真计算结果影响显著，通过对比不同时间步长下得到的仿真结果与试验测得的振荡频率，本文设定时间步长为0.01 ms。

图9 边界条件设置

表1 数值仿真参数设置

在仿真和试验结果中振荡频率良好匹配的基础上，从喷雾锥角和流量分布方面进一步验证模型的准确性。由图8b可测得喷雾锥角为41.2°，仿真结果误差仅为2.6%。VOF 模型为连续相模型，结合2.5 mm 的外流场网格尺度，计算的喷雾结果为团状，无法真实模拟出喷雾破碎分散的现象，导致数值模拟计算的喷雾锥角小于试验测得结果，且存在系统测量误差，故认为锥角的误差在合理范围。

图10 所示为试验工况下距喷嘴出口200 mm 处X方向上流量分布情况的试验和仿真结果。由图10 可知，试验和仿真所得的流量分布曲线重合度较高，均呈双峰型。仿真流量分布的峰值和谷值都稍大于试验值，2 个峰值的间距小于试验结果。这是因为试验中压力表测得0.2 MPa 的位置与喷嘴间存在一段橡胶管，受管壁沿程阻力损失影响，实际入口压力略小于0.2 MPa，同时，数值计算无法模拟喷雾破碎，导致喷雾锥角偏小。

图10 仿真与试验的流量分布对比

对比仿真和试验得到的喷雾结果，误差在合理的范围内，因此本文所建立的振荡式喷嘴射流计算模型能够用于射流特性的进一步研究分析。

4 计算结果及分析

对于前风窗玻璃的清洗，理想的状况是在使用较少清洗液且不影响驾驶者视线的同时，使得清洗液更广泛地分布在玻璃表面，避免雨刮器干刮而降低其寿命和清洗效率，因此对喷嘴的雾化效果有着较高的要求。而外流场是喷嘴性能的直接具体体现，因此本文探究振荡式喷嘴的外流场特性及其侧壁张角对喷雾特性的影响。

4.1 振荡式喷嘴外流场特性

试验工况下外流场第60～65 ms的水相体积分数云图如图11所示，可以观察到喷雾主要集中在两侧，中间区域雾滴分布较少且平均。这是因为射流在靠近壁面区域完成摆动方向的切换，摆动速度较小，相对喷雾中间区域而言停留时间长。振荡式喷嘴的这种流量分布特点使得在驾驶过程中清洗前风窗玻璃时，驾驶者的主要视线区域分布较少的喷雾，减少对驾驶者视线的干扰。射流左右摆动，并且第60 ms 时刻与第65 ms 时刻的外部射流云图一致，呈现出明显的周期性。

图11 第60～65 ms时刻水相体积分数云图

如图12 所示为试验工况下第69 ms 时刻的外流场速度云图及速度矢量图。从图12a可见，扇形喷雾两侧速度明显较中间区域高，但边缘高速区并不连续，高速喷雾以液滴团状形式存在。因为射流在靠近壁面区域的摆动速度较小，即液滴速度在X轴方向上的分量小，在Y轴方向的分量大。同时，距喷嘴出口越近，高速区越明显，距离出口0.15 m后，液滴团消失，这是因为射流破碎成了较小的液滴，在与空气的相互作用下，速度不断降低且趋于均匀。从图12b可见，靠近喷嘴出口处的扇形喷雾边缘外侧存在速度矢量，表明出口附近射流对空气扰动明显。

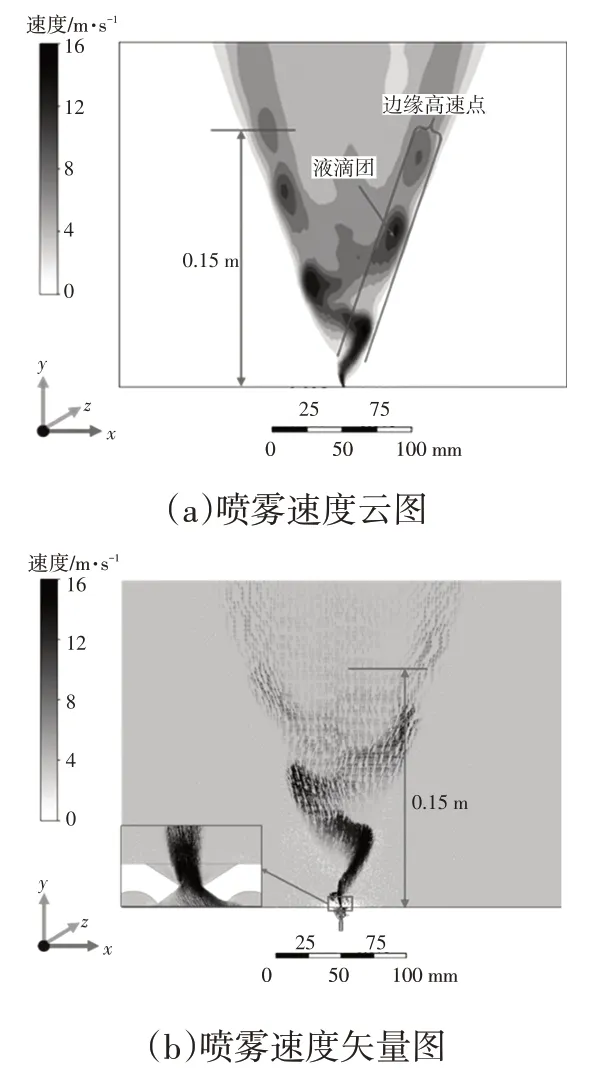
图12 射流速度云图及速度矢量图

4.2 侧壁张角θ对喷雾特性的影响

振荡式喷嘴结构见图6b。在试验喷嘴模型的结构基础上设侧壁张角分别为25°、26°、27°、28°、29°，其余结构尺寸不变，获得不同侧壁张角θ的喷嘴模型。在网格划分方法及尺度相同的前提下，对比不同侧壁张角下的喷雾特性。仿真中，喷嘴入口压力为0.2 MPa、出口压力为0。

图13 展示了不同侧壁张角θ下的射流振荡频率和平均流量。由图13 可知，θ=25°时的振荡频率为200 Hz，随着θ的增大，射流振荡频率逐渐减小，θ=29°时下降至191 Hz。振荡是湍流的随机性和附壁效应[2-5]综合作用的结果。内流道速度场如图14所示，由图14可知，主射流先后附壁于内流道两侧壁面，壁面张角与射流振荡密切相关，改变侧壁张角将会改变侧壁与内流道主射流之间的空间，影响主射流在喷嘴振荡腔中的切换行程。不同侧壁张角下的切换行程如图15 所示，由图15可知，θ变大导致射流在喷嘴内部摆动的行程增大。而当喷嘴入口压力和环境背压不变时，内流道主射流摆动速度变化很小，在摆动速度不变的前提下切换行程增大导致周期变长，又因外部射流的摆动受内部主射流直接驱动，因而外部射流的振荡频率下降。

图13 不同侧壁张角下射流振荡频率和平均流量

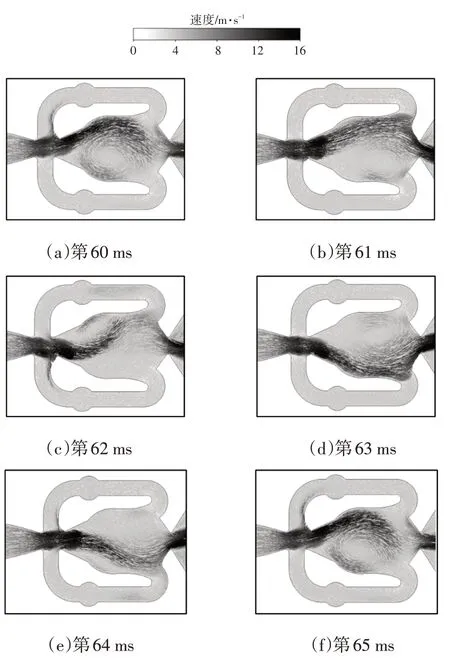
图14 试验工况下内流道速度场

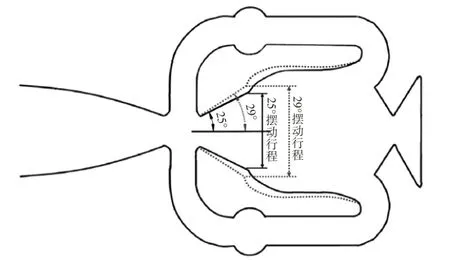
图15 不同侧壁张角下的切换行程对比

同时观察到，不同壁面张角的喷嘴之间流量相差较小，都在9.65 g/s 左右，流量的相对极差Rr和变异系数Cv为：式中，xmax和xmin分别为测量值中的最大值和最小值；μ为平均值；σ为标准差。

计算可得，Rr=1.79%，Cv=0.754%，所以侧壁张角在25°～29°的范围内时，可以认为壁面张角对振荡式喷嘴的流量系数没有影响。分析原因认为，喷嘴流量主要由喷射压力与环境背压的比值及喷嘴出口的尺寸所决定，喷嘴其余结构尺寸的改变对流量影响不大。

图16 所示为不同侧壁张角下喷嘴的喷雾水相体积分数云图，由图16 可以看出，不同侧壁张角下，流量分布仍然呈现双峰型。图17 所示为距离喷嘴出口200 mm处X轴位置在-42～42 mm范围内低流量区的流量占总流量的百分比。由图17 可知，低流量区的流量占比随侧壁张角的增大而增大，侧壁张角θ越大，切换行程越长，导致内部射流摆动过程在中间停留时间占比增加，进而导致外部射流低流量区分布了更多喷雾，其流量占比增加。

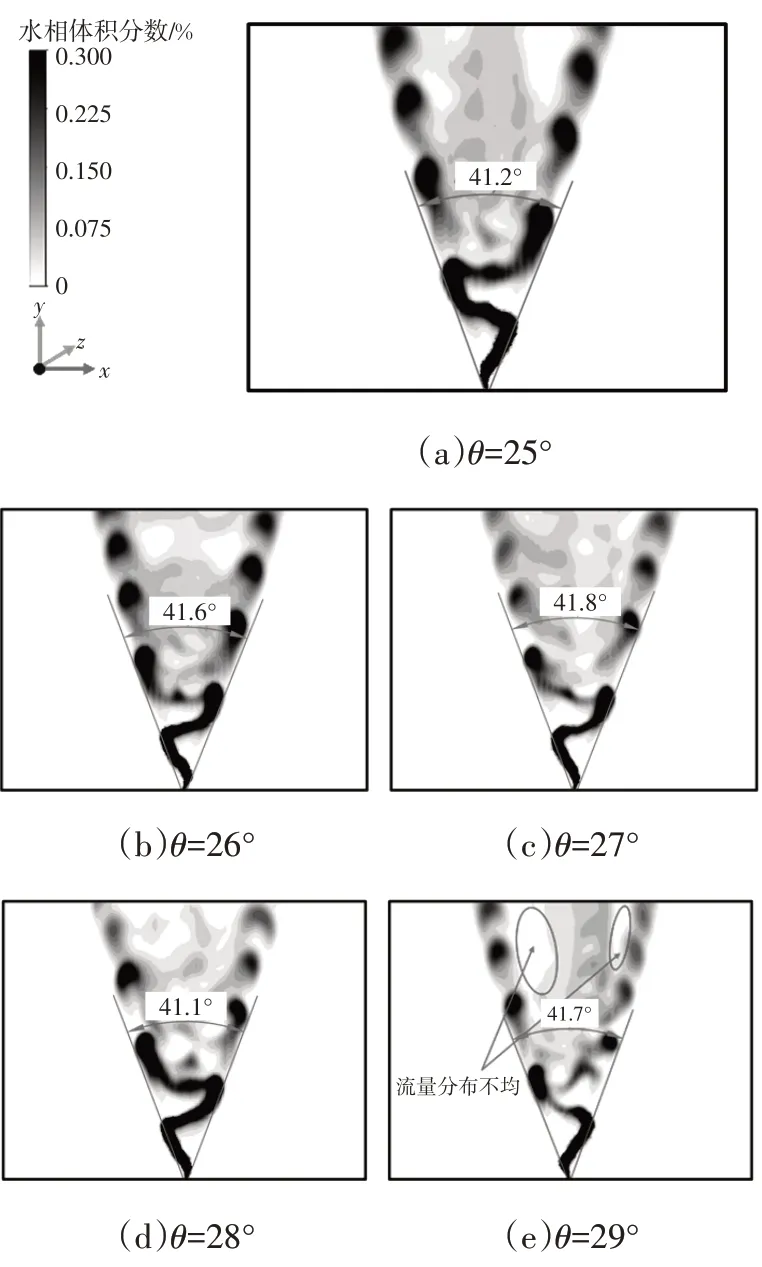
图16 各侧壁张角下喷雾水相体积云图

图17 各侧壁张角下中间区域流量占比

但从图16 中可以看出，虽然低流量区流量占比随着侧壁张角增大而增加，但其分布更加不平均。同时，由图16可测得各壁面张角下喷雾锥角均在41°左右，其相对极差为2.89%，变异系数为1.20%，可以认为侧壁张角对振荡式喷嘴的喷雾锥角没有影响。

5 结束语

本文基于某款振荡式喷嘴，通过自主设计流量收集装置及高速纹影试验测量获得其流量分布、喷雾锥角和振荡频率，建立数值仿真模型，研究了喷嘴内流道壁面张角对低压振荡式喷嘴喷雾性能的影响规律，从振荡频率、流量大小及分布和喷雾锥角多个方面进行了对比分析。在喷嘴入口压力为0.2 MPa、背压为环境压力条件下，侧壁张角在25°～29°的范围内，得到如下结论：

a.随着侧壁张角的增大，射流摆动周期变长，导致外部射流振荡频率减小。较高的振荡频率有利于射流雾化，因此在一定范围内，振荡式喷嘴的内流道侧壁张角应取较小的值，以获得更好的雾化效果。

b.不同侧壁张角下喷雾流量分布均呈现两侧高中间低的双峰形式，流量大小区别不大。随着侧壁张角的增大，低流量区流量占比增加，但分布更不均匀，有可能造成雨刮器的干刮，降低其寿命和清洗效率。

c.侧壁张角的改变不影响喷雾锥角大小。