基于脉振高频注入的船舶电机无传感器低速控制研究

张周　马继先

摘 要：船舶推进电机苛刻的工作环境凸显出机械式位置传感器不耐腐蚀等诸多弊端，因此，无位置传感器控制便成了目前永磁同步电机的研究趋势。传统的无传感器控制技术依赖基波数学模型致使其在低转速范围内控制失效，为了实现船舶电机低速范围内的转速估计，针对内置式永磁同步电机（interior permanent magnet synchronous motor，IPMSM）采用高频脉振信号注入法，并通过基于位置跟踪观测器的方法获取转子转速。利用Matlab对电机控制系统进行仿真验证，验证控制系统对转子位置以及转速估算的准确性。

关键词：IPMSM;脉振高频注入;无传感器控制;低速位置估计

中图分类号：TM351            文献标识码：A            文章编号：1006—7973（2019）05-0078-03

为了获得稳定且灵活的船舶动力，主推电机选用永磁同步电机能很好地满足需求。传统的船舶电机推进装置装有位置传感器，然而机械式位置传感器不耐风浪侵蚀，影响船舶推进系统的稳定运行。无传感器永磁同步电机船舶推进可以解决这一问题。目前无传感器控制技术的应用获得了诸多成效[1-3]，但是普遍依赖电机定子基波数学模型。这类方法在电机刚启动时或低速运行范围内时，难以从定子侧提取有用信号，最终导致位置判别失效[4-6]。R. D. Lorenz提出的高频信号注入法是解决该问题的一个有效方法[7]。

本文设计了脉振高频信号注入下的船舶电机无传感器低速控制系统。建立高频脉振信号激励下的IPMSM数学模型，阐述基于位置跟踪观测器的转子位置估算方法，分析无传感器控制系统原理，并通过仿真结果验证低速运行状态下无传感器系统的有效性。

1 高频脉振电压激励下的IPMSM电流响应

图1  实际转子-坐标系与估计转子-坐标系间的关系[1]

（1）坐标系中高频激励下三相IPMSM的电压方程[2]

因为高频时定子电阻相对于电抗小很多，这里忽略不计。

（2）坐标系中三相IPMSM定子电感

经过反Park变换将式（2）转化到两相静止坐标系中 ：

式中：是平均电感，是半差电感。

（3）实际转子坐标系中高频电压电流的关系无法估算实际的转子磁极位置，因此通过式（1）、式（3）以及图1中得到估计转子坐标系中高频电压和响应电流的关系：

式中：、以及、是估計转子-坐标系中电压、电流高频分量。

（4）为了尽量减小注入高频电压后给电机转矩带来的波动，只在轴注入的脉振高频注电压，轴不注入任何信号

此时的高频响应电流可以表示为：

式（6）中：是注入电压的频率，若，转子估计误差角将同时取决于轴和轴电流分量。其中，当时，，可以对轴电流作滤波提取，将幅值限定在一定范围。

2 转子位置估算方法

2.1 基于位置跟踪观测器的转子位置估算方法

船用IPMSM实现无传感器位置观测需要对高频响应电流进行一系列处理。先将定子侧轴高频响应电流通过一个带通滤波器BPF，去除基波频率分量以及高次干扰项，只提取其中一定幅值范围的电流信号。再通过直线拟合的方式将该该信号经低通滤波器LPF处理，即可获得位置观测器的入口信号，具体处理过程如下所示：

式中：若令，转子位置估计误差角也向零趋近。说明这样的调制方式可使转子位置估计值贴近实际值，达到估算目的。由上式可以看出，电机电感大小虽然影响的幅值，但是最终目的不是观测幅值而是观测。同时表达式中也不含转子角速度，因此这种方法既不受电机参数影响也不受转子角速度的影响，完全能满足低转速范围内的电机控制。

2.2 位置跟踪观测器

图2是依据外差法模型建立的观测器模块，主要包括PI调节器和电机机械特性数学模型。、和搭建的调节器能使入口信号调节至零，不断调节使估计值更加精确。图中，是估计系统中的转矩，引入的目的是提高观测器模块的响应速度，当然特定系统中也可以直接给定。

3 脉振高频注入的船用IPMSM控制系统设计

IPMSM控制系统组成。图3是船用永磁同步电机无传感器控制系统结构框图，系统由船用IPMSM、逆变驱动模块、位置估算算法、滤波电路等模块构成。图4是脉振电压信号注入的电机控制系统原理框图。由于高频响应电流中掺杂了基波电流、PWM开关频率谐波电流等掺杂信号，可以通过带通滤波器（BPF）将其滤除，从而提取出包含转子位置信息有用信号。

4 仿真验证

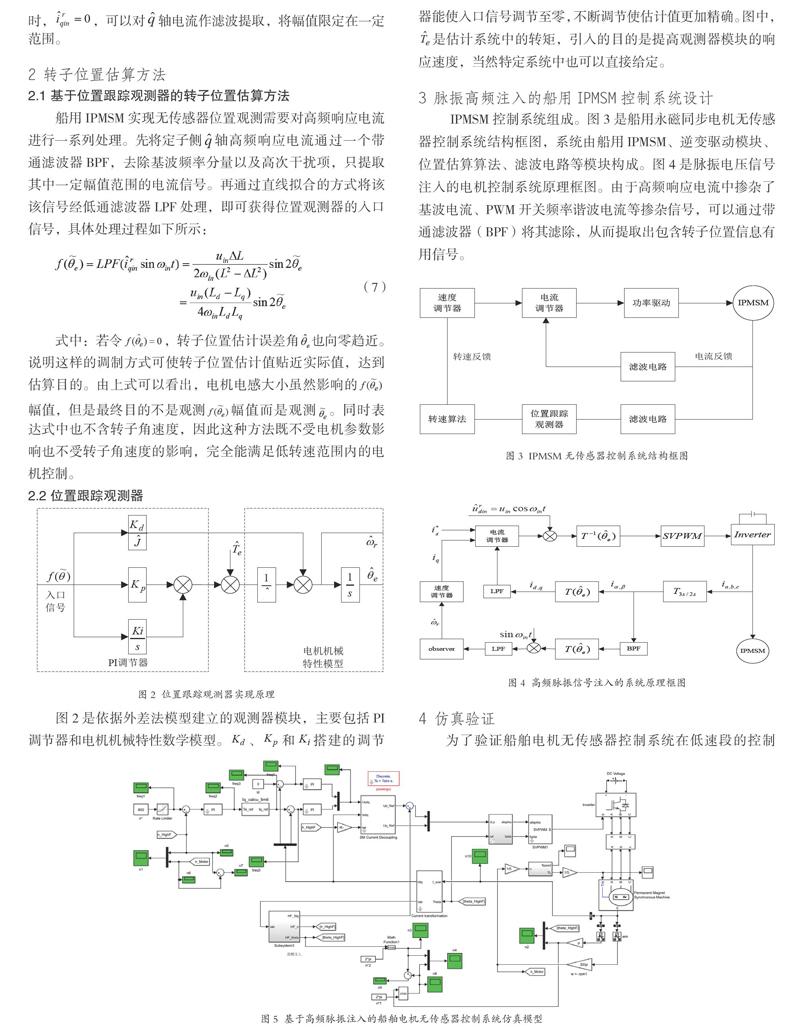
为了验证船舶电机无传感器控制系统在低速段的控制效果，在前述低速控制模型的基础上上搭载上螺旋桨负载，根据图4所示的理框图在Simulink仿真环境下搭建系统运行模型。电机参数选取为：额定电压380V，，，，，，极对数，给定转速为。电机系统仿真模型如图5所示;图6为电机转速估算值与实际值变化曲线，估算曲线与实际曲线能很好地拟合，能将估计误差控制在极小的范围，电机启动瞬间出现短时波动并迅速过渡到稳定值，并且持续稳定在给定值;图7为转速误差曲线，估计误差稳定在0值附近，波动极小;图8为转子位置估计值与实际值变化曲线，估算曲线与实际曲线能很好地拟合，位置波形也有规律地往返;图9是转子位置估计误差曲线。

5 结束语

本文对基于脉振高频注入的船舶电机无传感器低速控制研究得出以下结论：

（1）采用脉振高频电压信号注入法，在电机低速运行时能够实现对转子位置及转速的准确跟踪。

（2）基于位置跟踪观测器的转子位置估计方法能使转子位置估计值很好地收敛到实际值，实现了对转子的位置估计。

参考文献：

[1] 周复. 高性能无传感器PMSMs控制系统的研究与应用[D]. 东华大学， 2009.

[2] 王剑飞， 胡书举， 李建林， 鄂春良. 永磁直驱型风力发电机的无传感器控制研究[J]. 电力电子技术， 2009， 43（03）： 6-8.

[3] 秦俊峰， 曾江黎， 彭亚东， 白洪芬. 船舶电推PMSM无位置传感器控制研究现状综述[J].钦州学院学报， 2017， 32（07）： 1-4+10.

[4] 杨立永， 谢晓峰， 陈智刚. 基于反电动势PLL法的PMSM无传感器控制研究[J]. 电力电子技术， 2016， 50（12）： 88-90.

[5] 易伯瑜，康龙云，陶思念，等. 基于两段卡尔曼滤波器的内置式永磁电机观测器设计[J]. 电工技术学报， 2014， 29（9）： 110-118.

[6]薛树功，魏利胜，凌有铸.基于扩展卡尔曼滤波的永磁同步电机无传感器矢量控制[J].电机与控制应用，2011，38（08）：15-18.

[7] Raca D， Harke M C， Lorenz R D. Robust magnet polarity estimation for initialization of PM synchronous machines with near-zero saliency[J]. IEEE Transactions on Industry Applications， 2008， 44（4）：1199-1209.