基于离散曲率的温室CO2优化调控模型研究
胡 瑾 田紫薇 汪健康 卢有琦 辛萍萍,3 张海辉
(1.西北农林科技大学机械与电子工程学院, 陕西杨凌 712100;2.农业农村部农业物联网重点实验室, 陕西杨凌 712100;3.陕西省农业信息感知与智能服务重点实验室, 陕西杨凌 712100)
0 引言
CO2是绿色植物光合作用的主要原料之一,对作物生长发育和物质积累至关重要[1]。但由于温室相对密闭,一天中随着温室光照强度和温度条件的变化,作物对CO2的需求也会发生改变,导致CO2供需不匹配[2-4]。适宜的CO2浓度将有效促进作物生长,不足或过高时将对作物产生有害影响[5-9]。在CO2浓度较低或者中等阶段,光合速率随着CO2浓度增加而快速增大,CO2是影响该阶段光合速率的主要因素,当CO2超过一定浓度达到限制点后,光合速率增长幅度逐渐变小[10],若仍大量增加CO2,对植物光合速率提升效果不明显且耗费大量资源。因此,探寻适宜作物生长的CO2浓度,建立融合调控效益的CO2优化调控模型,已成为设施农业中CO2环境高效调控亟待解决的问题。
近年来,CO2环境调控方法已成为研究热点。文献[11]研究了生理生化CO2响应模型,从生理角度分析了CO2响应的影响因素。文献[12]研究了日光温室草莓光合特性及其对CO2浓度升高的响应,并从生理角度分析原因,为CO2调控奠定生理基础。文献[13]研究发现,CO2浓度在(800±25)~(1 000±25) μmol/mol范围内时,番茄结果期叶片光合速率调控效果很好,为我国北方地区温室番茄结果期的生产实践提供了理论参考依据。文献[14]对开花期番茄增施1 000~1 300 μmol/mol的CO2,可较大提高番茄单叶净光合速率。以上研究在固定范围内进行CO2调控,该区域也就是CO2对光合速率影响由强变弱的变化区,而光照强度和温度等其他因素也会对CO2限制点产生动态影响,因此该类方法虽然一定程度提升了光合效率,但难以真正实现高效精准调控。文献[15-16]建立了番茄不同生长期的光合速率预测模型,实现了不同含水率下以CO2饱和点为目标值的精准预测,为温室CO2气肥自动调控提供了理论依据和决策支持。文献[17]建立了温度、光强与作物生长阶段的CO2饱和点之间的对应关系,以CO2饱和浓度为目标值进行动态最优调控。文献[18]提出了融合支持向量机-改进型鱼群算法的CO2优化调控模型,在不同温度、光照强度组合条件下动态预测CO2饱和点,为CO2精准调控提供定量依据。上述方法均以CO2饱和点进行调控,而其位于CO2浓度较高阶段时,随着CO2浓度的增加,CO2响应曲线增加趋势变缓直至下降,因此以CO2饱和点进行调控,虽然可以达到最大光合速率,但造成资源浪费与调控效益下降。根据以上分析,如果采用CO2响应曲线中光合速率由快速增加变为缓慢上升的特征点作为目标点,可实现在保证作物光合需求的条件下最大程度提升CO2调控效率。曲率作为一种常用的曲线评价指标被用于曲线特征点的提取[19],并初步在农业数据分析中得到应用,如文献[20]应用最大曲率点实现了夏玉米物候期的生长状态转换时间的获取。因此探寻CO2响应曲线曲率最大点成为提升CO2调控效益的关键。
针对上述问题,在考虑光合速率与调控效益的前提下,本文以初花期温室番茄为试验材料,研究构建基于支持向量机回归算法(SVR)的光合速率预测模型,并对不同温光条件下的CO2响应曲线进行离散曲率计算与最大值寻优,从而获取曲率最大值点对应的CO2浓度,以此构建基于离散曲率的CO2优化调控模型,为温室CO2的精准高效调控和节本增效提供定量依据。
1 材料与方法
1.1 试验材料
试验于2018年9—10月在西北农林科技大学泾阳蔬菜试验示范站温室内进行。试验地位于北纬34°26′、东经108°7′,属于暖温带半干旱半湿润大陆性季风气候,年均日照时数2 163.8 h,年均辐射总量479.9 kJ/m2,年均积温4 811℃,年均气温12.9℃[21]。以番茄品种“金棚8B”为试材,在培养皿中将已经浸胀的种子进行催芽,待要萌发时进行低温处理,在72孔穴盘内采用营养钵育苗。育苗基质为农业育苗专用基质,其营养含量为有机质质量分数50%以上,基质孔隙度约60%,pH值6~7。幼苗培育期间,保持水肥充足,待番茄幼苗叶片为5片左右,选择长势均匀的番茄幼苗进行移植。待番茄第1朵花苞开放,选择茎的横径0.8~1.2 cm、株高25 cm左右的健康植株进行光合速率测试。试验期间,施肥、浇水等田间管理均正常进行,不喷施任何农药和激素。
1.2 试验方法
试验选取茁壮的番茄180株作为样本,采用美国LI-COR公司的LI-6800型便携式光合仪测定温度、光照强度和CO2耦合下的CO2响应曲线,同时为避开光合“午休现象”对试验数据的影响,选择在09:00—11:30和14:30—17:30进行试验数据采集。选择自顶叶往下的第5片功能叶片作为试验样本。在试验过程中采用光合仪选配的多个子模块按需控制叶室环境参数。其中,利用控温模块设定16、20、24、28、32、36℃等6个温度梯度,利用LED(Light emitting diode)光源模块获得0、200、400、600、800、1 000、1 300、1 600、1 900、2 200 μmol/(m2·s)等10个光子通量密度梯度,共形成60组嵌套试验条件。由于光合仪CO2注入系统中CO2混合浓度可控范围是0~2 500 μmol/mol,故每组试验利用CO2注入模块设定20个CO2浓度测试点,分别为0、50、100、200、300、400、500、600、700、800、900、1 000、1 100、1 200、1 300、1 500、1 700、1 900、2 100、2 300 μmol/mol,共获取1 200个测量数据。在同一植株功能叶片上每个测量环境条件进行3次重复,剔除错误数据后取平均,共获取1 200个有效试验数据。
2 模型构建
本文分3步构建CO2优化调控模型。首先基于光合试验数据建立光合速率预测模型;其次,基于光合速率预测模型获取不同光照强度和温度下的CO2浓度和光合速率关系曲线,并基于L弦长离散曲率法对曲线进行曲率计算;最后,对曲线的离散曲率进行最大值寻优,获取CO2效益优化调控目标值,以此构建CO2优化调控模型。
2.1 多因子耦合的光合速率预测模型
将试验所得的数据集随机分为训练集和测试集,即选取960组数据作为训练集(占总数据集的80%),剩下240组数据作为测试集(占总数据集的20%)。针对样本数据特点以及高精度要求,选取SVR算法[22]进行光合速率预测模型的构建。基于试验所得到的数据,以温度、光照强度、CO2浓度作为输入样本,以光合速率作为输出样本,采用SVR算法构建光合速率预测模型,进行光合速率的拟合预测,其具体流程如图1所示。
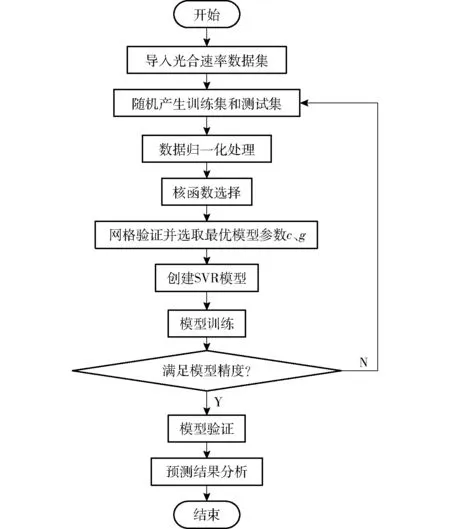
图1 支持向量机回归建模流程图Fig.1 Flow chart of support vector regression modeling
为避免大数据淹没小数据现象,以及便于神经网络预测与曲率计算,首先,将数据集进行归一化操作。其次,确定SVR关键参数。由于径向基核函数计算的复杂度不随参数变化而变化,故选取其作为核函数;惩罚因子c为对误差的宽容度,c过大,容易导致模型过拟合,c过小,容易导致模型欠拟合;影响因子g隐含地决定了数据映射到新的特征空间后的分布。经网格验证方法进行多次经验计算获取最佳参数值惩罚因子c为3.00,影响因子g为3.41。最后,训练及构建模型。针对960组训练集,采用径向基核函数,通过低维空间的非线性不可分问题映射到高维空间,并在高维空间产生用于最优分类的超平面,进行线性回归决策分析。
2.2 基于L弦长曲率法的CO2响应曲线曲率最大点获取
2.2.1L弦长曲率法的原理
在CO2响应曲线中,首个曲率最大点代表着CO2浓度对净光合速率影响程度由强到弱的特征点位,是构建CO2优化调控模型的关键。根据有限个数据点拟合的CO2响应曲线无法采用连续曲线曲率法,而离散曲率法不需要具体的公式便可计算曲率,文献[23]提出的一种离散曲率计算方法——L弦长曲率,在局部区域计算曲率,不受整条曲线的全局影响,且与曲线的真实曲率之间存在密切联系。
L弦长曲率法依赖输入的参数L,根据拓扑距离获取目标点处前后距离为L的点来确定它的支持领域,并应用线性插值提高曲率计算精度。曲线上某点pi的L弦长曲率的计算主要分为两个步骤:①pi点的支持领域获取,如图2所示。②将支持领域前后端点之间的欧氏距离与参数2L作比值,然后应用和该比值平方与数字1的差值相关的一个根号值作为离散曲率。
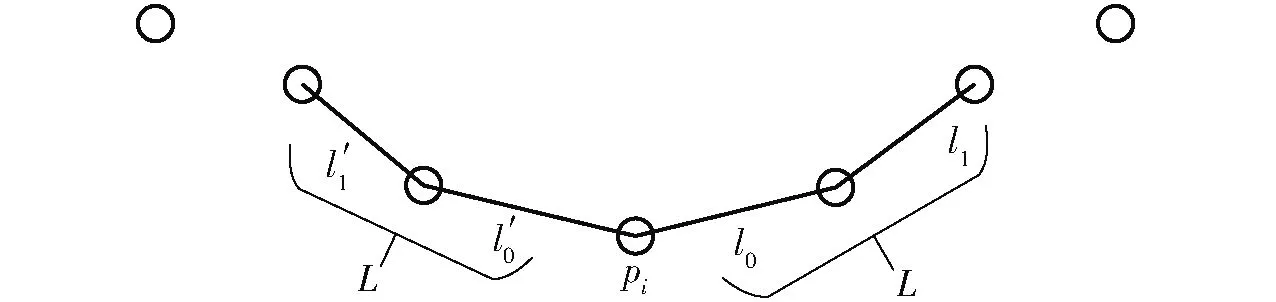
图2 pi点的支持领域Fig.2 Supporting area of pi
2.2.2L弦长曲率计算和最大值寻优
CO2响应曲线离散曲率最大点的获取方法主要包括两方面内容,首先在不同光温嵌套条件获取CO2响应曲线,其次进行L弦长曲率计算和最大值寻优。
(1)获取不同光温嵌套条件下的CO2响应数字曲线
通过调用已建立的SVR光合速率预测模型网络,获取不同温度和光照强度嵌套条件下CO2浓度与光合速率的关系曲线。每组CO2响应曲线曲率的获取均建立在特定温度、光照强度基础上。温度以1℃为步长,建立曲率获取温度条件数据样本集Ti=(T1,T2,…,T21),其中Ti=16+(i-1),i∈[1,21]区间的整数。光照强度以50 μmol/(m2·s)为步长,建立曲率获取光照强度条件数据样本Pj=(P1,P2,…,P41),其中Pj=200+50(j-1),j∈[1,41]区间的整数。在16~36℃和200~2 200 μmol/(m2·s)范围内,完成预测模型对温度、光照强度的实例化,从而建立不同光温条件下的CO2响应曲线。
(2)采用L弦长曲率计算和寻优

(1)
其中
(2)
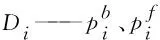
si——离散曲率符号
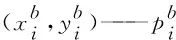
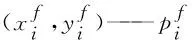
si为正表示曲线在当前点呈凸性,反之呈凹性;为避免实验数据微小波动导致响应曲线的凹凸性发生改变从而无法准确获取离散曲率最大值,因此本文在计算离散曲率时将符号统一取为正号。
按照以上步骤对响应曲线各点求L弦长曲率,并应用爬山法[24]寻优得到曲率最大值。记录和保存其对应的CO2浓度,直到获取所有响应曲线曲率最大点对应的CO2浓度。
2.3 CO2优化调控模型构建
基于上述寻优方法,得到了温度、光照强度为输入,CO2响应曲线离散曲率最大点对应的CO2浓度为输出的861组目标CO2浓度数据集,采用SVR算法进行CO2优化调控模型构建。随机选取训练集与测试集并进行归一化处理。针对861组目标CO2浓度数据集,随机选取689组样本数据(约占总样本的80%)作为训练集,172组(约占总样本的20%)作为测试集,用于模型验证。选择径向基核函数参与模型训练,确定最佳参数c为1.00,g为4.91,以此完成CO2优化调控模型的构建。
3 结果分析
3.1 光合速率预测模型验证结果
为了验证SVR构建预测模型的拟合效果,同时采用BP(Back propagation)神经网络和非线性回归多项式构建拟合预测模型,三者的模型评价对比如表1所示。由表1可见,SVR构建预测模型的决定系数最高,为0.98;均方根误差与平均绝对误差均最小,分别为1.79 μmol/(m2·s)和1.21 μmol/(m2·s)。
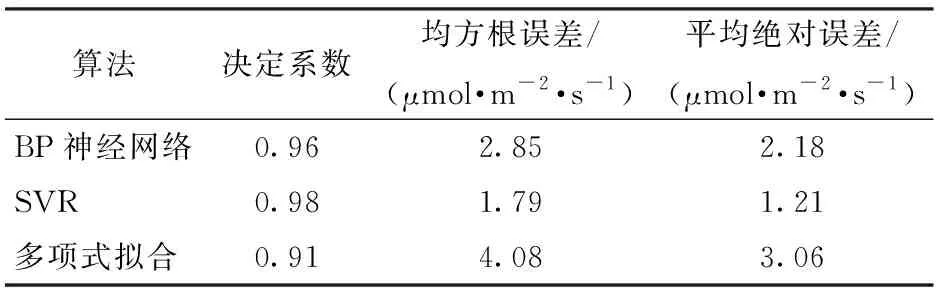
表1 3种建模方法的预测模型评价指标对比Tab.1 Comparison of prediction model indicators for three modeling methods
证明SVR算法对于本文多维样本数据拟合具有优势,采用SVR算法构建预测模型是可行的。
为进一步验证SVR预测模型的预测效果,将SVR预测模型与CO2经典响应模型进行对比。目前被普遍应用于植物生理生态等方面研究的 CO2经典响应模型有直角双曲线模型、Michealis-Menten模型和直角双曲线修正模型等[25]。因此选取以上3种CO2经典响应模型对60组嵌套条件下的试验数据进行拟合,并将这3种模型的评价指标绘制成盒图,如图3所示。

图3 3种CO2经典响应模型评价指标对比Fig.3 Comparison of evaluation indexes of three typical models
由图3可发现,直角双曲线修正模型决定系数所处范围的上下界均高于其他两种模型,均方根误差所处范围上下界均小于其他两种模型,说明3种典型模型中,直角双曲线修正模型对本文试验数据的拟合效果最好。因此,进一步采用直角双曲线修正模型与本文SVR预测模型进行对比,以此验证SVR预测模型的拟合效果。通过对比可以发现,直角双曲线修正模型的决定系数范围为0.97~0.99,均方根误差范围为0.07~1.81 μmol/(m2·s);SVR预测模型的决定系数为0.98,均方根误差为1.79 μmol/(m2·s),均位于直角双曲线修正模型相应评价指标的范围之内。这说明,SVR预测模型的拟合效果与直角双曲修正模型的拟合效果很接近。但是直角双曲线修正模型无法预测实测点之外的数据,而SVR预测模型可在保证与直角双曲线修正模型相近精度的情况下实现对非试验条件样本的预测,可解决试验样本不足的问题。
采用异校验方式应用验证集对光合预测模型的泛化能力进行验证,得到光合速率实测值和预测值相关性如图4所示。图中直线L1为测试集数据实际值和预测值的拟合直线,其斜率为0.95,截距为0.47,说明预测值与实测值相关性较高。
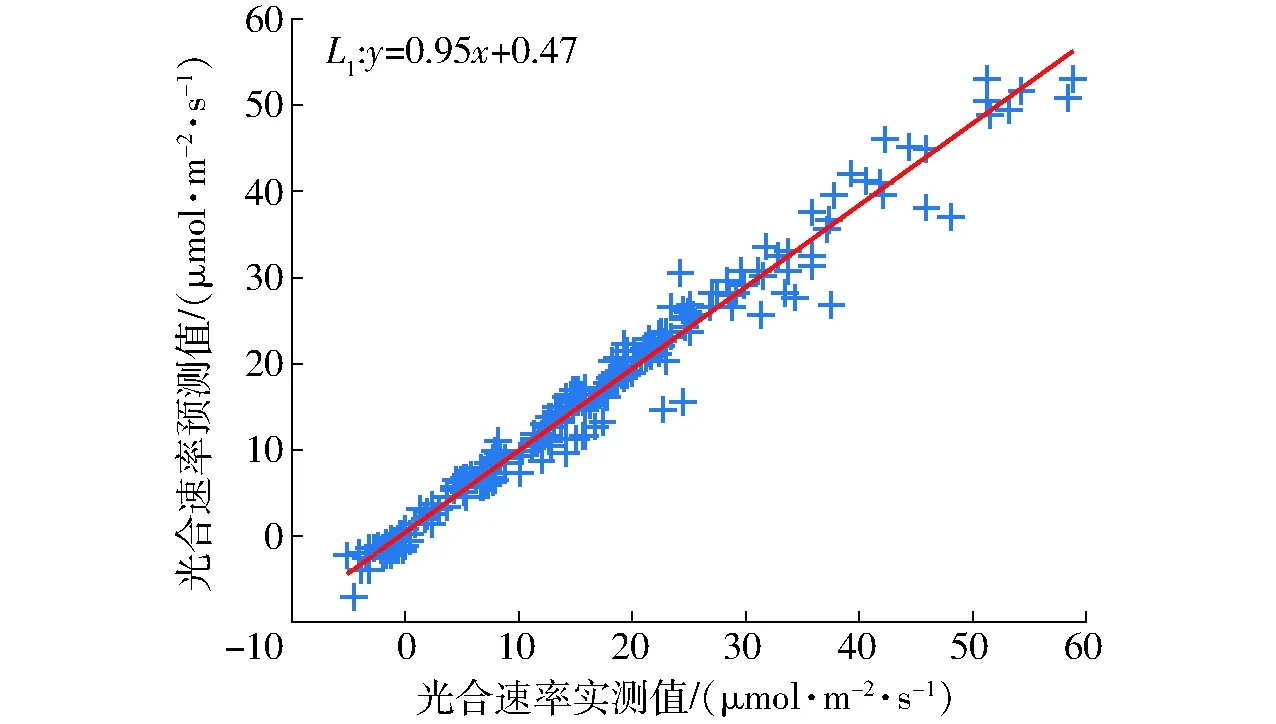
图4 SVR光合速率预测模型验证Fig.4 SVR predictive model verification
3.2 离散曲率最大值点获取
在建模过程中累计获得861组不同条件下的曲率最大点,由于无法完全罗列,下文仅展示温度从19℃到34℃区间内以3℃为步长,光照强度从200 μmol/(m2·s)到2 200 μmol/(m2·s)区间内以200 μmol/(m2·s)为步长条件下的CO2响应曲线曲率及曲率最大值点的获取结果,如图5所示。同时,为了对比曲率最大点与CO2饱和点的效果,本文采取与文献[18]中相同的方法获取CO2饱和点,最后得到CO2响应曲线中曲率最大点和CO2饱和点的对比关系图,其中曲率最大点为点状标记,CO2饱和点为圆圈状标记。
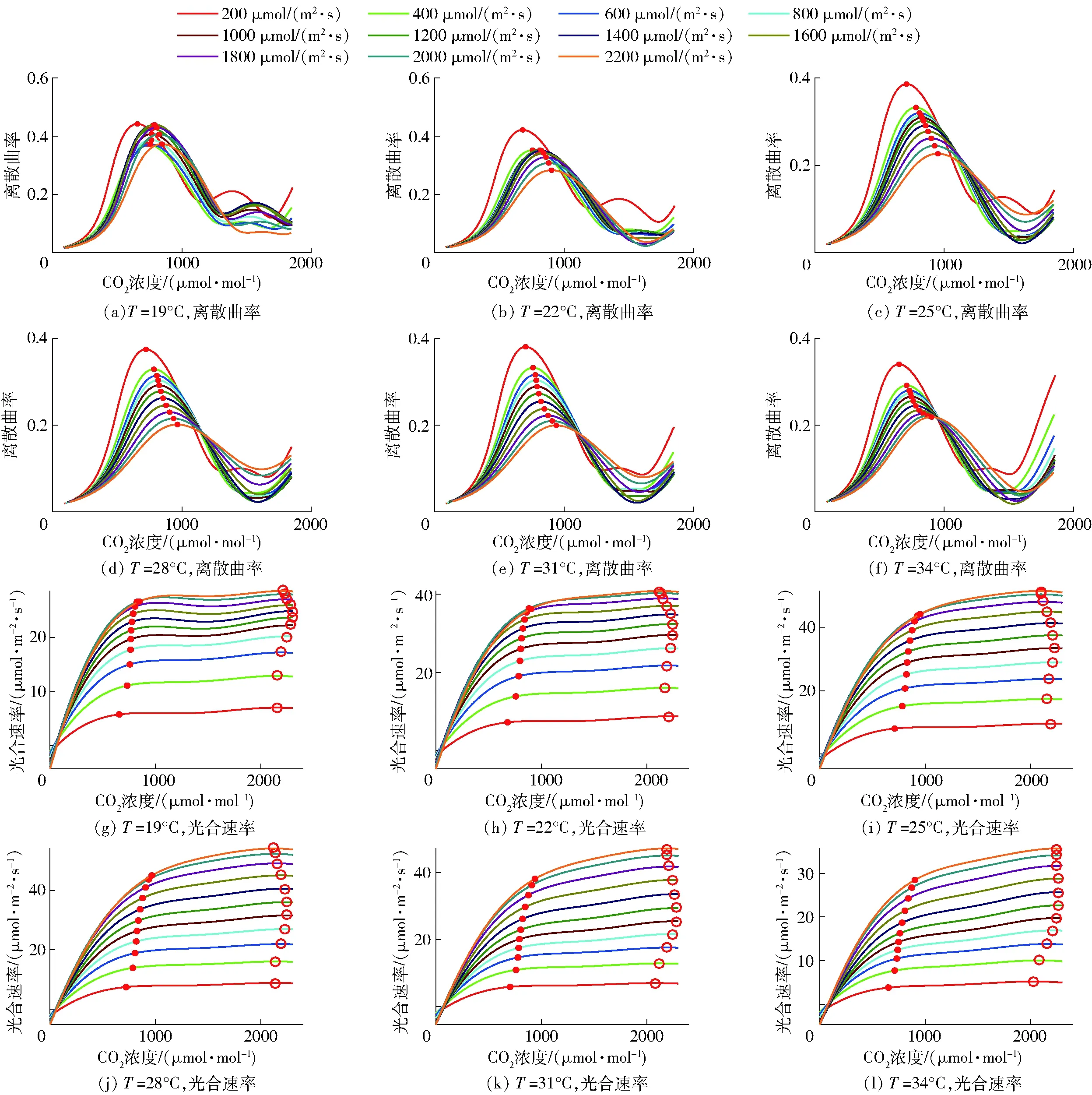
图5 CO2响应曲线特征点获取与效果对比Fig.5 Acquisition of characteristic points of CO2 response curves and comparison of effect
由图5可发现,定义离散曲率图中首个曲率最大值点代表CO2浓度对光合速率影响程度从强到弱的特征点位,刚好对应于光合速率图中相应曲线的增长速率转折点,这说明L弦长曲率法可以提供准确的CO2调控目标点。由光合速率图可以发现,在特征点位之前,光合速率随着CO2浓度增加而快速上升;越过该点后,大量补充CO2直到CO2饱和点,只能促进光合速率少量提高,造成CO2补充效益降低。进一步分析发现,所有特征点位对应的CO2浓度均在600~1 000 μmol/mol范围内;所有的CO2饱和点变化不大,且都在曲线末端区域,即2 000~2 300 μmol/mol范围以内。以上分析结果与文献[19]构建的CO2优化调控模型预测 CO2饱和点位于1 800~2 400 μmol/mol区间基本一致。
进一步分析光合速率图中不同环境下曲率特征点和CO2饱和点的变化,可以发现同一光照强度下,CO2曲率特征点和CO2饱和点随着温度的增加呈现先增后减的趋势;同一温度下,随着光照强度的增加,CO2曲率特征点对应的CO2浓度一直升高;而CO2饱和点浓度呈现先升后降的趋势。在较低或中等光照强度条件下,CO2饱和点浓度随着光照强度的增加而增加,当光强增加到1 000 μmol/(m2·s)至1 400 μmol/(m2·s)范围内时,CO2饱和点浓度开始下降,与文献[18]中CO2饱和点浓度随着光照强度的增加呈现先升后降趋势的现象一致。以上分析说明了不同温度和光强下CO2曲率特征点和饱和点均存在差异。
3.3 CO2优化调控模型结果及验证
为了验证基于SVR算法构建的番茄CO2优化调控模型的拟合效果,本文同时采用BP神经网络和非线性回归多项式拟合两种方法构建调控模型,模型评价对比如表2所示。
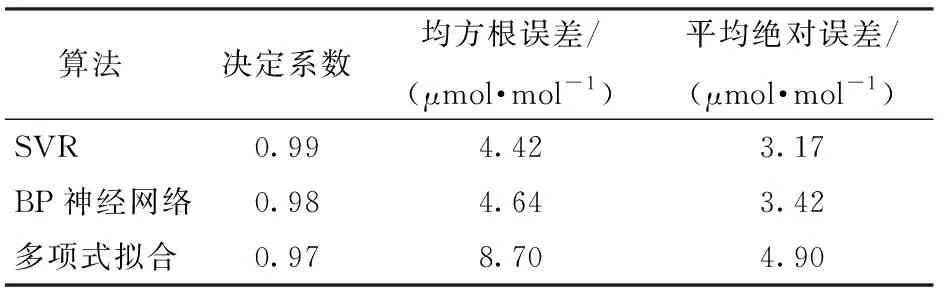
表2 3种建模方法的调控模型评价指标对比Tab.2 Comparison of control model indicators for three modeling methods
由表2可见,SVR模型的决定系数最高,为0.99;均方根误差和平均绝对误差最低,分别为4.42 μmol/mol和3.17 μmol/mol,SVR算法构建的CO2调控目标值模型具有更高的精准度和拟合效果,具体模型如图6所示。由图6可发现,当温度和光照强度较低时,CO2调控目标值较低;在温度一定时,CO2调控目标值随着光照强度的增加而升高;当光照强度一定时,随着温度的增加,CO2调控目标值呈现先升后降的趋势,与作物生长需求一致。
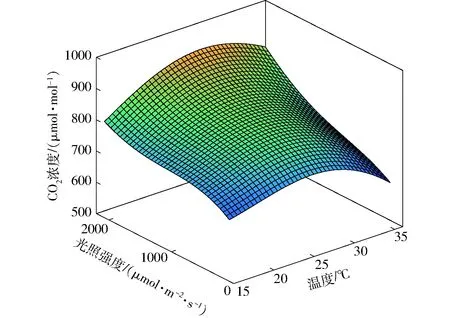
图6 CO2优化调控模型Fig.6 CO2 optimal regulation model
为了进一步证明调控模型精准性,本文采用相同试验样品测量了60组不同光温条件下的CO2响应曲线,并利用CO2响应直角双曲线修正模型[11]进行响应曲线拟合,最后通过连续曲率法实现了不同响应曲线曲率最大值获取,以此作为调控目标的实测值。同时,将 CO2优化调控模型获取的调控目标值作为预测值,进行调控模型验证,相关性如图7所示。分析可知,图中直线L2为实际值和预测值的拟合直线,斜率为0.98,截距为19。可见,本文构建的CO2优化调控模型能准确预测CO2效益优化点,为CO2的精准高效调控提供了定量依据。
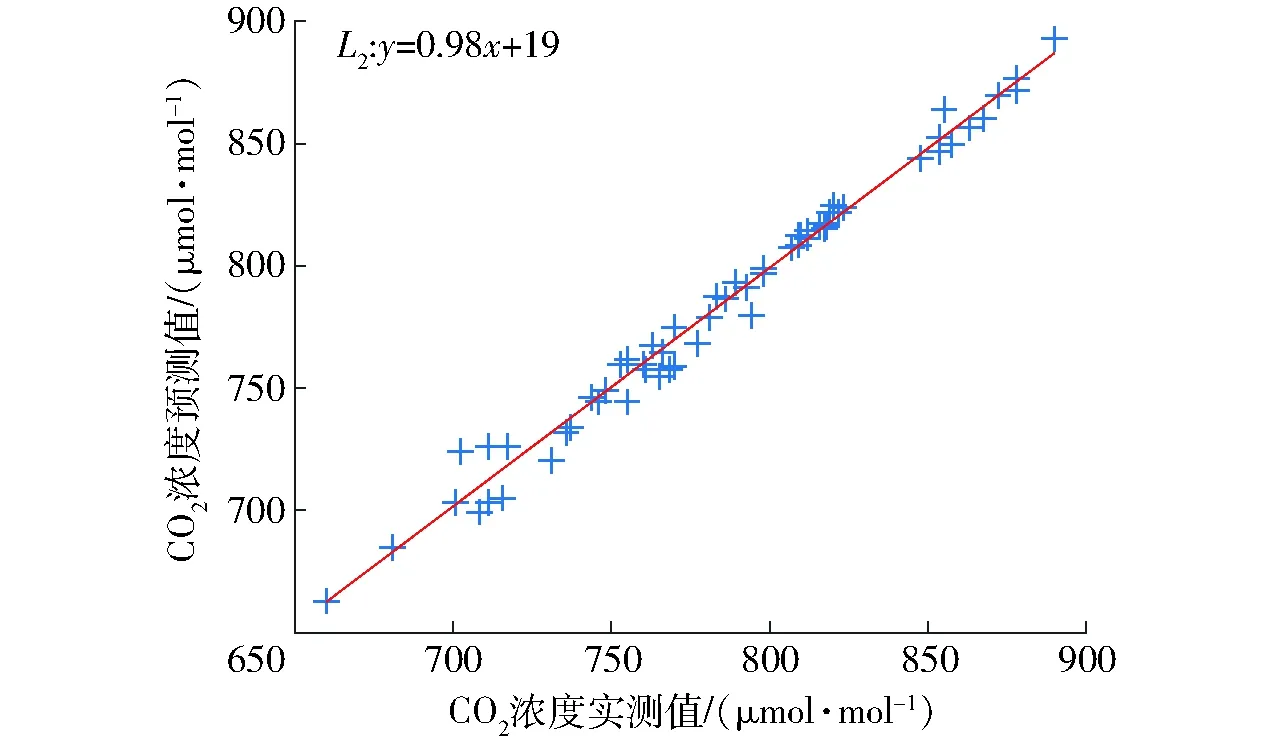
图7 CO2优化调控模型验证Fig.7 Regulatory model verification of CO2
3.4 调控效果对比
3.4.1理论调控效果分析
为了进一步验证CO2优化调控模型的调控效果,与获取CO2饱和点作为调控目标值的传统方法[18]进行效果比较。在温度试验区间内以6℃的温度梯度为例,对比结果如表3所示。从表3中可以发现,所有光温耦合条件下,CO2供需量的大幅度下降均只造成光合速率的少量降低。本文获取离散曲率最大点对应的CO2浓度作为目标值,相比于CO2饱和点目标值的方法,CO2供需量平均下降61.81%,光合速率平均仅减少15.58%。说明采用该方法构建不同温度、不同光照强度条件下的CO2优化调控模型具有高效节能特点,可为设施作物CO2环境优化调控提供理论基础。
3.4.2实际调控效果分析
为了验证本模型的实际调控效果,在西北农林科技大学泾阳蔬菜试验示范站的温室内开展调控模型验证试验,试验采用自行研制的CO2闭环调控系统构建验证系统,系统工作流程如图8所示。传感器实时监测温室内的CO2浓度、光照强度和温度等环境信息,并传送给决策节点。决策节点基于实时环境信息,利用树莓派中内嵌的CO2优化调控模型计算CO2调控目标值。然后,根据实时CO2浓度和调控目标值,判断是否需要进行调控。若当前浓度高于目标值,则不进行调控,继续进行调控目标值的计算与比较;若当前浓度低于目标值,则进行动态CO2差值计算,发出CO2调控信号,打开调控设备中CO2发生器的电磁阀,释放对应体积的CO2,然后关闭电磁阀,等待10 min使CO2分布均匀,然后再返回到决策节点。
试验分别在同一温室的3块大小相同的区域内进行,利用塑料膜实现3块区域之间的空间隔离,对比曲率组、饱和组、自然组3组的调控效果。试验中运行CO2曲率最大点模型和CO2饱和值模型,采用曲率最大点和饱和点作为目标值分别对限制点区和饱和点区进行调控,自然对照区为自然条件不进行CO2补充。试验于07:00开始,采用LI-6800型便携式光合速率测试仪对不同试验区的番茄进行光合速率测量,不同试验区域光合速率变化趋势基本一致,其中得到6月3日的番茄光合速率时变化趋势如图9所示,当天温室内温度和光照强度的变化趋势如图10所示。由图9可发现,曲率组光合速率整体比饱和组低15.14%,补充CO2供需量降低57.61%;曲率组光合速率整体比自然组高26.70%。说明以曲率最大点为调控目标值的CO2调控模型可以在提高光合速率的情况下大幅度减小CO2供需量,对融合效益的CO2精准调控具有实际指导意义。由图10可以发现,温度和光照强度随着时间的推移有着明显的变化,本文提出的CO2优化调控模型可以基于实时环境对CO2调控目标值进行动态、高效的获取。

表3 曲率特征点与CO2饱和点对比Tab.3 Comparison of characteristic value and conventional value in two methods

图8 CO2调控流程图Fig.8 Flow chart of CO2 control
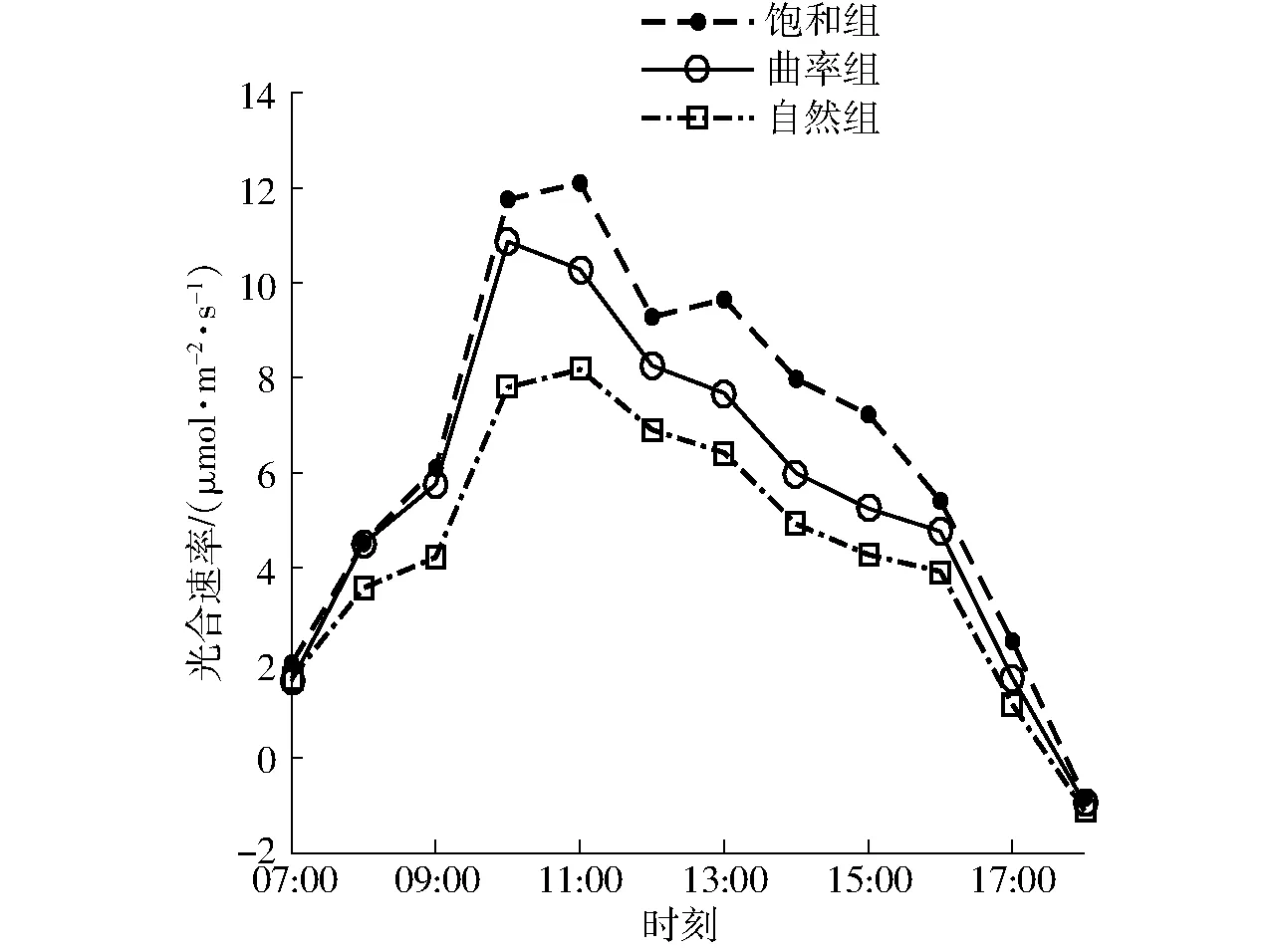
图9 3组光合速率的变化趋势Fig.9 Comparison of variation trend of photosynthetic rate

图10 温度和光照强度的变化趋势Fig.10 Variation trends of temperature and light intensity
4 结论
(1)结合番茄植株CO2响应特点建立了一种番茄初花期CO2优化调控模型。以温度、光照强度、CO2浓度等多因子耦合嵌套所得净光合速率试验结果为基础,采用SVR算法构建所得光合速率预测模型,决定系数为0.98,较非线性回归多项式拟合和BP神经网络构建的预测模型,能以更高精度拟合多因子输入情况下的光合速率。
(2)提出基于L弦长曲率理论的CO2响应曲线离散曲率计算方法,可获取CO2响应曲线曲率最大点,求得CO2效益优化调控目标值,从而满足CO2按需调控且节能高效的要求,为设施作物优产优质,增大效益奠定了良好的基础。
(3)基于SVR算法构建以CO2效益优先值为调控目标值的调控模型,决定系数为0.99,均方根误差为4.42 μmol/mol,平均绝对误差为3.17 μmol/mol,拟合效果好。与CO2饱和点调控方式对比,光合速率平均减少15.58%,但CO2供需量平均下降61.81%。验证试验中光合速率较饱和点调控时仅下降15.14%,但CO2供需量平均下降57.61%;相较自然条件下光合速率升高26.70%。因此,本文提出模型能够兼顾作物需求和效益,可为实现设施作物动态、高效CO2调控提供理论依据。

