基于K-means聚类与RBFNN的点云DEM构建方法

赵庆展 李沛婷 马永建 田文忠

(1.石河子大学信息科学与技术学院， 石河子 832003； 2.国家遥感中心新疆兵团分部， 石河子 832003；3.兵团空间信息工程技术研究中心， 石河子 832003； 4.石河子大学机械电气工程学院， 石河子 832003)

0 引言

数字高程模型(Digital elevation model，DEM)是地形高程信息的数字化表示，是重要的基本地形产品之一[1]，不仅可以非常直观地显示地形和地貌，而且为各种地形特征的定量分析和不同类型专题图的绘制提供了基本数据[2]。无人机机载激光雷达(Light detection and ranging，LiDAR)是集激光测距技术、计算机技术、高精度动态惯性导航系统(Inertial navigation system，INS)和高精度动态差分全球定位系统(Differential global positioning system，DGPS)等于一体的摄影测量新技术[3]，可提供地物三维空间坐标、地物激光回波强度、获取时间等信息[4]。因无人机机载LiDAR具有起降灵活、机动性好等优点而被广泛应用，可直接获取高精度、高密度点云数据以生成DEM。

同时，点云滤波是生成DEM的基础，即把点云分成地面点与非地面点。林祥国等[5]采用多基元三角网渐进加密方法实现点云滤波，使滤波误差降低。李鹏程等[6]基于表面实现点云滤波，即采用点云的波形信息进行加权曲面拟合以获取点云表面。张继贤等[7]利用K-means聚类方法快速分割点云中的电线。周晓明[8]结合点云全波形属性信息和聚类方法实现滤波。综上，具有代表性的点云滤波方法可以分为基于逐渐加密、基于表面和基于聚类等方法[9]。本文选择原理简单、且便于处理海量数据的K-means聚类方法实现点云滤波。

神经网络不需建立精确的数学模型即可实现非线性映射，以预测相关数据。KUÇAK等[10]利用自组织映射神经网络和K-means聚类两种方法，结合点云法向量、强度和曲率3种属性信息，实现点云分割，以生成DEM。ZUO等[11]采用神经网络实现城市点云分类，以验证神经网络可以成功分离地面点、建筑物、树木和裸露土等地物。径向基函数神经网络(Radical basis function neural network，RBFNN)以其学习速度快、不易陷入局部极小值等优点，常被应用在数据插值预测中。陈昌华等[12]利用主成分分析方法消除径向基函数神经网络(RBFNN)输入层数据的相关性，即以主成分分析模型的结果作为RBFNN的输入，建立土壤水分的预测模型，结果表明，RBFNN预测精度比误差反向传播神经网络预测精度高。周仲礼等[13]采用模拟退火蚁群算法改进径向基函数神经网络模型，分别对地层高程进行面插值和对矿体品位进行空间体插值，且与普通克里金(Kriging)插值方法进行交叉验证，结果表明，改进径向基函数神经网络插值效果明显优于克里金插值方法。目前使用径向基函数神经网络实现点云预测的研究较少[14]，本文使用径向基函数神经网络预测地面点云高程值，且采用Delaunay三角网生成DEM。

1 数据获取

以AeroScout B1-100型单旋翼油动无人机作为飞行平台，搭载Riegl VUX-1型激光扫描仪、OxTS Survey+2型惯性导航系统和Sony可见光相机获取研究区LiDAR数据和可见光数据。无人机的长、宽、高为3.3 m×1.0 m×1.3 m，尾旋翼直径0.65 m，空机质量50 kg，有效载荷18 kg，发动机功率13.23 kW，标准油箱容积10 L。Riegl VUX-1型激光扫描仪是专业测绘级激光扫描仪，扫描方式为线性扫描，近红外波长，最大转速200 r/s，激光脉冲频率高达550 kHz，记录16 bit的回波强度。Riegl VUX-1型激光扫描仪详细参数见表1。

表1 Riegl VUX-1型激光扫描仪产品参数Tab.1 Product parameters of Riegl VUX-1 laser scanner

研究区域位于新疆兵团第八师一五零团五连周边荒漠植被区，地理位置为44°57′29″～44°58′0″N，85°58′35″～85°59′4″E，激光雷达数据基本包含了荒漠植被区的部分植物类型，主要以梭梭、骆驼蓬、麻黄、碱蓬草、驼绒藜为主。获取数据的飞行任务参数设置如下：航高60 m，巡航速度6 m/s，航线3条。在采用Riegl LMS配套软件和OxTS NAVgraph配套软件对激光雷达数据进行配准、校正、平差和删除噪声点等预处理后，截取部分区域数据作为试验区，且以WGS-1984-UTM-Zone-44 N为投影坐标系导出.las格式的点云数据。为方便后期描述，令X、Y、Z、P分别表示由点云三维坐标和回波强度组成的N×1维矩阵，其中X和Y分别表示东向和北向的位置，单位为(°)，Z表示点云高程，单位为m。试验区点云总数N为69 544，点云X中元素的范围在-46.065°～-15.000°之间，Y中元素的范围在83.958°～112.145°之间，Z中元素的范围在275.863～280.535 m之间，P中元素的范围在12 036～49 850之间。

2 研究方法

2.1 零-均值标准化

因为K-means聚类方法需使用不同距离来度量数据相似性，所以为了消除数据量纲和取值范围差异的影响，需要将数据缩放到相同区间，即标准化[15]。同时，标准化后的数据也利于加快RBFNN的训练速度，提高预测的准确性[16]。常用的标准化方法有3种：最大-最小标准化、零-均值标准化和小数定位标准化。其中，最大-最小标准化容易受到数据最大值和最小值的影响，小数定位标准化中移动的小数位数取决于绝对值最大的样本点，故本文选择零-均值标准化，与其它两种标准化方法对比，零-均值标准化保持了异常值所包含的有用信息，标准化公式为

(1)

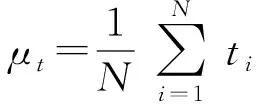
(2)

(3)

式中Snormal——点云属性t标准值

Sorigin——点云属性t原始值

μt——点云属性t的均值

σt——点云属性t的标准差

ti——点云属性t的第i个点

2.2 K-means聚类方法

2.2.1K-means聚类原理

K-means聚类方法是把数据分成k簇，使簇内数据具有较高的相似度，而不同簇之间数据相似度较低[17]，采用K-means聚类方法实现点云聚类获得地面点云的基本步骤如下：

(1)根据采集得到的研究区数据，确定需要的聚类数目k。

(2)确定k个聚类对象的初始聚类中心{Ui|i=1，2，…，k}。

(3)分别计算每个样本数据到k个聚类中心的距离。

(4)筛选样本数据到聚类中心的最小距离，且将此样本划分到聚类最小的类别中。

(5)当所有样本点都划分完毕，重新计算k个对象的聚类中心。

(6)与前一次获取的k个聚类中心比较，判断聚类中心是否发生变化或达到预定的最大迭代次数。如果聚类中心发生变化，转到步骤(3)；如果聚类中心发生变化但已经达到最大迭代次数或者聚类中心没有发生变化，则算法终止[18]。

通常，采用不同的距离标准可以得到不同的聚类结果。本文选择适用范围较广的平方欧几里距离作为距离标准，其计算公式为

(4)

式中d(x,y)——属性t中样本点云x与样本点云y的欧几里距离

xt——属性t的样本点云x

yt——属性t的样本点云y

2.2.2肘方法确定最佳聚类数目

K-means聚类方法的难点之一是必须事先指定聚类数目k，k值的选择会严重影响聚类结果，故本文使用肘方法确定最佳聚类数目。基本思想是选择簇内误差平方和(Within-cluster sum of squared errors，SSE)(即聚类偏差)骤变时的k值[19]，此时对应的k值为最佳聚类数目。即先对不同聚类数目进行K-means聚类，然后根据聚类偏差得到不同k值的曲线，且绘制不同k值对应的聚类偏差图，最后找到聚类偏差最显著拐点处对应的k值，其中聚类偏差的计算公式为

(5)

其中

式中DSSE——簇j的聚类偏差

Bi——第i个点

U′j——簇j中心点

l——指定的最大聚类数目

K-means聚类方法的另一个难点是初始聚类中心的选择。为了得到最优的聚类结果，本文在随机选择初始聚类中心和采用肘方法最佳聚类数目的基础上，针对不同的随机初始中心独立运行K-means聚类方法多次，然后从中选择DSSE最小的模型作为最终模型。

2.3 点云抽稀

海量地面点云给后期处理带来较大影响，尤其是在数据处理速度方面[20]，故在保证研究对象的必要信息下，对高密度的点云进行抽稀有一定的实际意义。为了简化抽稀过程，本文按照比例对点云进行抽稀，且仅对比抽稀率为20%和80%的抽稀结果。

Kriging插值是一种统计插值方法，可以准确对表面预测，不仅考虑了待估点与已知点位置的相互关系，而且考虑了变量的空间相关性[21]，所以采用Kriging方法插值抽稀结果，获取较好的抽稀率。随机抽取100个地面点云作为检验数据集，然后对剩余地面点云进行抽稀率为20%和80%的抽稀，对抽稀后的点云进行点云高程插值。最后从插值结果中提取检验数据集的高程预测值，且通过点云的预测值与实测值进行对比分析。

均方根误差(RMSE)能够评判插值结果，均方根误差越小，表明插值精度越高，误差越小[22]，其计算公式为

(6)

式中RRMSE——点云高程的均方根误差

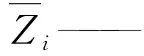
Zi——检验数据集中点云高程实测值

N′——检验数据集中点云数量

2.4 径向基函数神经网络模型

2.4.1RBFNN模型建立

RBFNN是应用多变量的径向基函数设计而成，由输入层、隐含层和输出层组成。RBFNN的输入层为n维向量I=(I1，I2，…，In)；隐含层为m维向量D=(D1，D2，…，Dm)；输出层为f(I)，即输出层是RBFNN的输入层对应的实测值，以此实现RBFNN模型的建立[23]，其输出公式为

(7)

其中

(8)

式中f(I)——径向基函数神经网络的输出层函数

Wi——第i个隐含层神经元到输出层神经元的权值

Di(I)——隐含层径向基函数，采用高斯函数

Ci——第i个隐含层神经元中基函数的中心

ri——第i个隐含层神经单元的宽度，调节网络的灵敏度

RBF神经网络模型设计结构如图1所示。

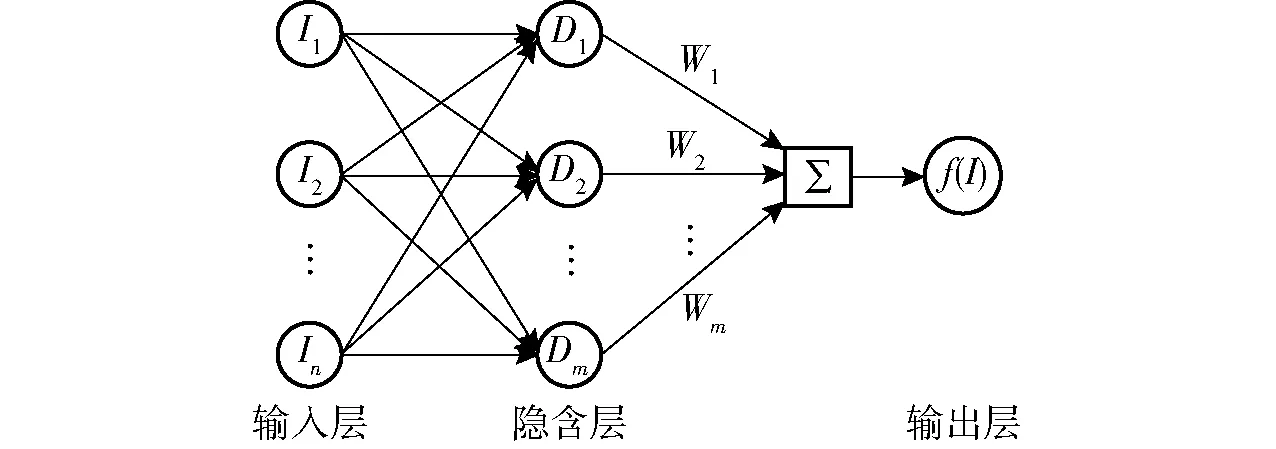
图1 RBF神经网络模型结构图Fig.1 RBFNN model structure

采用软件Matlab神经网络工具箱的newrb函数设计RBFNN，在进行径向基函数逼近时，newrb函数可以自动添加隐含层的神经元数量直到满足训练误差要求，其实现公式为

Nnet=newrb(I，T，Ggo，Ssp，Mmn，Ddf)

(9)

式中Nnet——训练得到的RBFNN

T——预测的目标数据

Ggo——RBFNN的目标误差

Ssp——径向基函数散布常数，默认值1

Mmn——最大神经元数量

Ddf——在网络训练过程中显示的频率，newrb中默认值为25

2.4.2RBFNN模型验证

为了验证模型的准确性，用测试点云对训练完成后的RBFNN模型进行测试，且与实测高程值进行对比分析，来检验RBFNN对点云高程预测的准确性。采用软件Matlab中sim函数，来实现测试点云高程的预测，计算公式为

A=sim(Nnet,Q)

(10)

式中A——点云高程预测值矩阵

Q——由测试数据集中点云坐标X、Y和回波强度P组成的矩阵

通过线性回归法对预测值和实测值进行分析，线性回归分析法是将实测值作为自变量，预测值作为因变量，建立一元线性回归方程，检验回归方程的决定系数R2。决定系数R2越接近1，则说明实测值和预测值吻合度越高，即预测效果越好。

3 结果分析

3.1 K-means聚类结果

采用软件Matlab提取研究区点云三维坐标和回波强度值，且对点云进行零-均值标准化处理。采用Python语言编程确定最佳聚类数目和实现K-means点云聚类方法，图2为聚类偏差结果，横坐标表示聚类数目，纵坐标表示聚类偏差。分析图2可知，当k为4时，聚类偏差呈现肘型，即对于研究区点云，最佳聚类数目为4，此时的聚类偏差DSSE为4 304.32。

图2 聚类偏差可视化Fig.2 Within-cluster sum of squared errors visualization

采用K-means聚类方法对回波强度进行k为4的聚类，设置聚类最大迭代次数为3 000、聚类误差为0.000 1。图3a为采用K-means聚类得到不同类别可视化结果，数据1、数据2、数据3和数据4分别对应簇1、簇2、簇3和簇4。图3b是簇1灰度图，通过目视检查分析可得，簇1包含研究区地面点云和离群点云，其点云总数为50 728，点云高度范围在275.863～279.636 m之间。K-means聚类得到的地面点云完整地保留了试验区真实地表起伏情况，但仍然存在少量离群点云，因此利用反复建立三角网滤出簇1中的少量离群点云，从而获取地面点云数为48 722，此时点云高度范围为275.870～277.600 m。

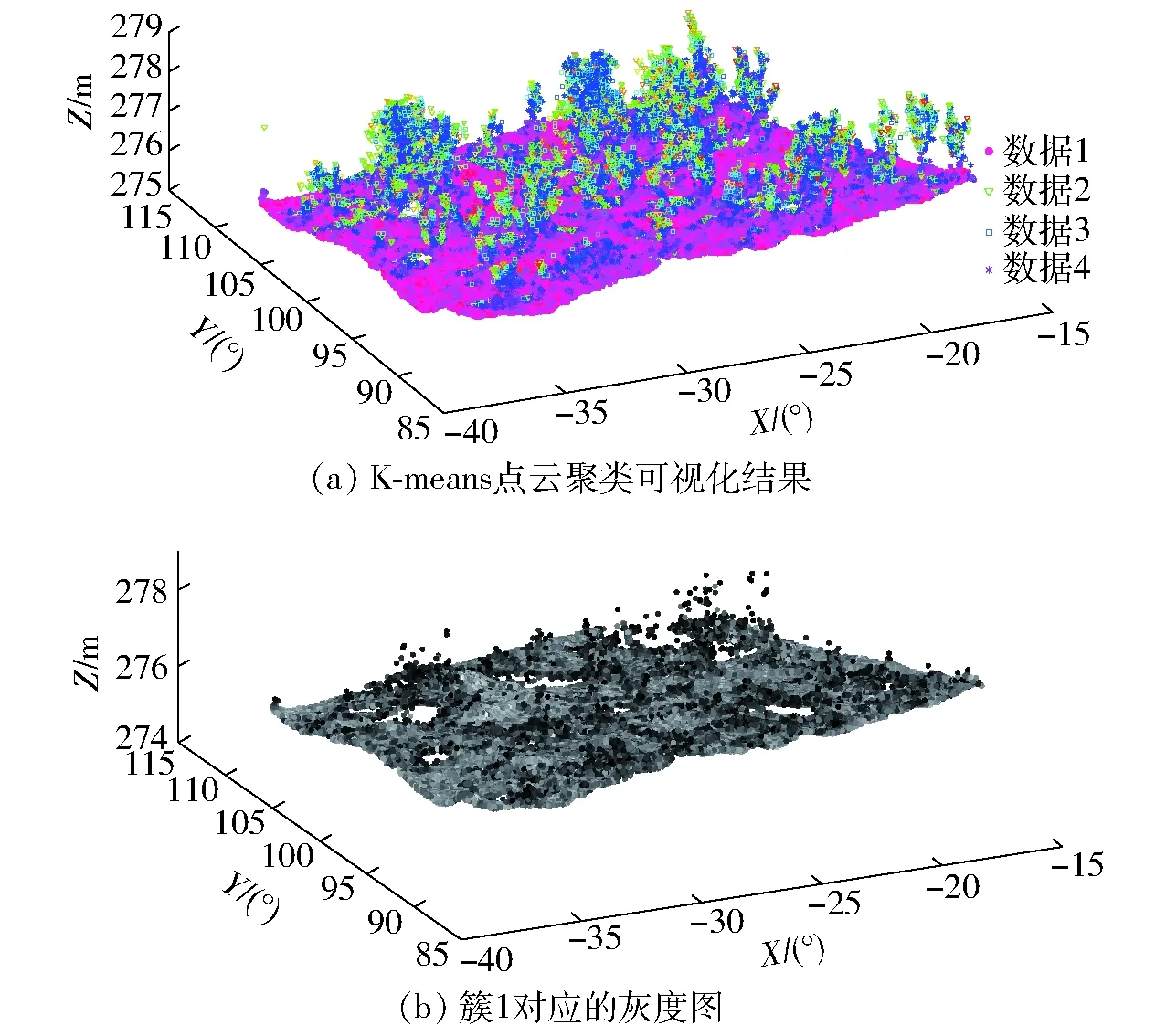
图3 K-means聚类三维可视化点云图Fig.3 Visualization point clouds by using K-means clustering method

3.2 克里金插值结果

通过计算均方根误差评价抽稀精度，可知采用20%和80%的抽稀率对应的均方根误差分别为0.021 m和0.023 m，即采用20%抽稀率抽稀可大大减少点云数据量。本文对地面点云进行抽稀处理后得到点云数为9 724。图4为20%抽稀率抽稀处理后的克里金插值可视化结果，其中绿色点表示经过抽稀后的点云，红色点表示100个检验点云。

图4 20%抽稀率抽稀后的克里金插值的可视化结果Fig.4 Visual Kriging interpolation result at 20% point cloud thinning rate

3.3 径向基函数神经网络训练结果

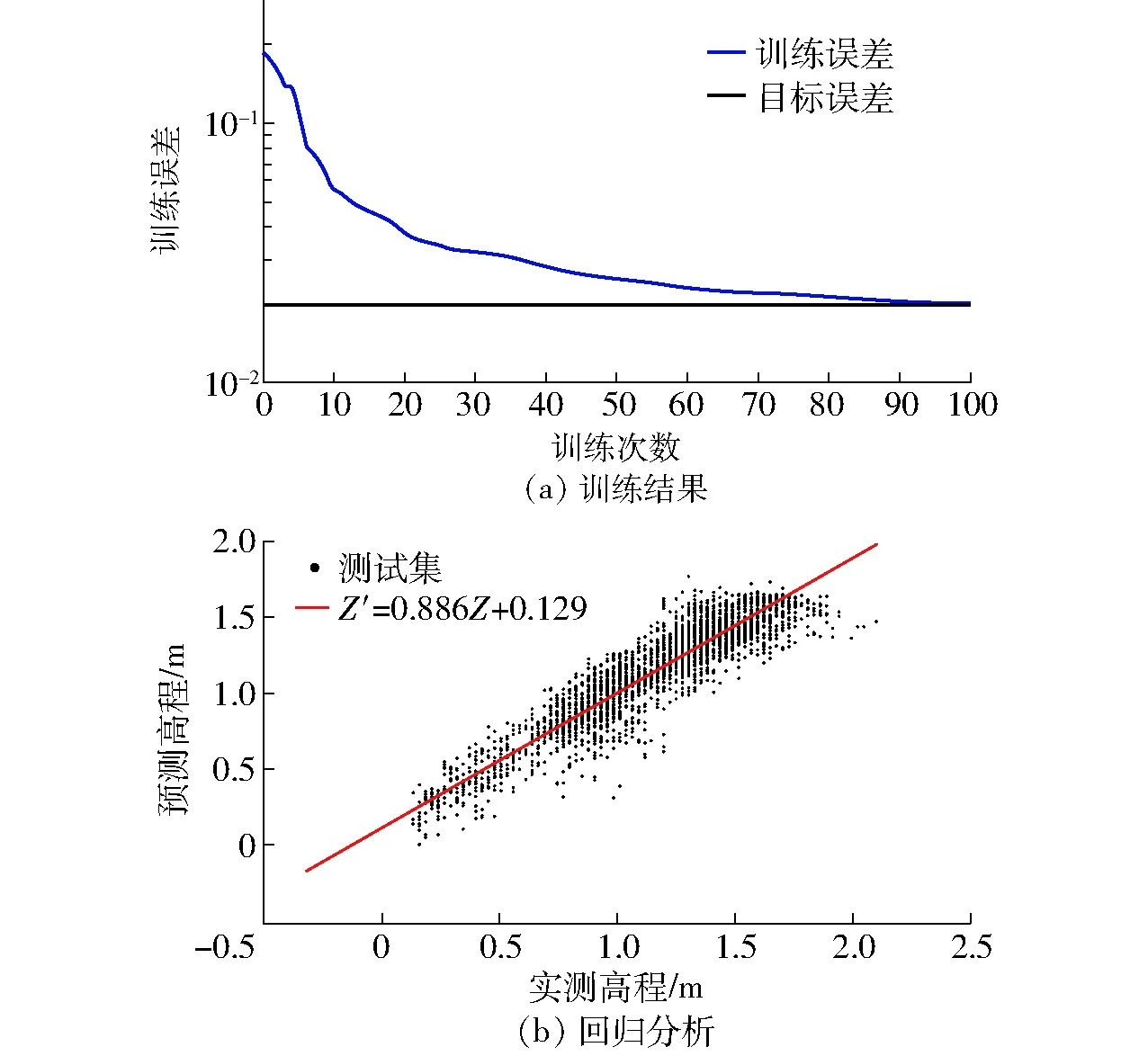
图5 RBFNN训练结果和线性回归分析Fig.5 Training results of RBFNN and regression results of RBFNN

随机采取抽稀后点云的70%作为RBFNN的训练数据集，30%作为评估网络的测试数据集。选择训练数据集中点云的X、Y坐标矩阵和回波强度矩阵P作为训练RBFNN的输入，即n=3，输入向量I=(I1,I2,I3)。把训练数据集中点云的高程Z作为网络的输出向量，即Z=f(I)。根据给定的目标误差，多次训练网络确定隐含层数量。建立输入层神经元数量为3，输出层神经元数量为1，训练误差为0.02，散布常数为1的RBFNN。图5a为RBFNN的训练结果，可以看出，训练次数达到100即隐含层神经元数量为100时，训练误差0.020 2很逼近目标误差0.02，对应的RBF训练时间为56 s。

利用训练完成的RBFNN对测试数据集进行插值预测高程，记录预测结果。同时采用线性回归法进行分析，图5b为RBFNN模型预测高程与实测高程的线性回归分析，对应的决定系数R2为0.887，说明预测值与实测值的拟合度较高。均方根误差RMSE为0.168 m，说明插值预测精度较高。

3.4 内插结果

根据训练完成的径向基函数神经网络，对抽稀后的地面点云高程值进行内插，且根据高程值构建Delaunay三角网以生成试验区DEM。图6为采用Delaunay三角网生成的DEM，共构建97 393个三角网。

图6 基于Delaunay三角网生成的DEM图Fig.6 Generated DEM diagram based on Delaunay triangulation network

4 讨论

本文目的是验证利用RBF神经网络内插值实现点云高程的预测，所以对K-means聚类结果仅采用了目视检查来定性评价聚类结果。在后续研究中，可以计算漏分误差、错分误差和总体误差来定量评价聚类结果。另外，如果需要提高K-means聚类速度，可以先采用K-means聚类对标准化处理的点云三维坐标进行聚类分簇，然后针对不同的簇，再次使用K-means聚类对回波强度标准值进行聚类，且合并每类地面点云。

本文随机选取100个点云测试Kriging插值结果，可知测试点分布较好，但是存在部分区域测试点分布较少，故后期可先计算点云曲率再抽稀。在建立RBF神经网络模型时，选择输入变量为点云坐标矩阵X、Y和点云回波强度矩阵P，并没有充分考虑到点云之间的相关性，因此RBF神经网络输入层数据的相关性还需进一步研究。

5 结论

(1)采用K-means聚类方法实现点云滤波获得试验区48 722个地面点云，采用肘方法确定最佳聚类数目为4，采用Python语言编程设置聚类数目、最大迭代次数3 000和聚类误差0.000 1等参数，不仅可以快速得到聚类结果，而且可以将K-means聚类独立运行多次，选择最小聚类偏差DSSE为4 304.32作为最终结果。

(2)在保证用最少的数据量表示地面真实状况下，选择简单、运算速度快的抽稀方法。在ArcGIS软件中按比例对点云进行抽稀，且采用Kriging插值方法对不同抽稀后的点云进行插值。通过比较插值结果，得到较优抽稀率为20%。将RBF神经网络引入到点云处理过程中，尝试建立一种快速高效的空间预测方法，从误差分析可以看出，RBF神经网络对空间数据具有较好的预测能力，预测时间为56 s，其预测的决定系数R2为0.887。