基于卡尔曼滤波离散滑模控制的明轮船直线跟踪
洪剑青 赵德安 孙月平 张 军 刘 波 刘晓洋
(1.江苏大学电气信息工程学院, 镇江 212013; 2.镇江高等专科学校现代装备制造学院, 镇江 212028)
0 引言
随着人民生活水平的提高,人们对水产品的需求不断增长,极大地促进了水产养殖业的飞速发展[1-3]。水产养殖业已成为国民经济不可缺少的组成部分,年产值高达几百亿元。规模化生产促使水产养殖业向集约化、自动化、信息化、智能化的方向发展[4-7]。
养殖水域通常水情比较复杂,水下植物较多。明轮船具有吃水浅、适航性好的特点,适宜作为水面作业装备的载体。水上作业装备实现智能化、自动化、信息化作业的方式,不仅可以提高作业效率、降低人力成本,克服工作时间的限制,且更加贴近养殖动物的生活习性[8-9]。
明轮船的航迹跟踪是近来研究的热点。文献[9]建立了明轮船的水动力模型和控制方程。文献[8,10]详细给出明轮船航迹跟踪系统的硬件方案和模糊控制航迹跟踪方法[8,10-12],实现了基本的跟踪。文献[13-14]采取鲁棒预测控制、障碍李亚普诺夫函数法,取得较好的控制效果,但是由于预测控制采取在线连续时域滚动计算,算法复杂、计算量较大、计算耗时和对系统计算资源需求较高、对反馈信号实时性要求较高;障碍李亚普诺夫函数法存在反步微分爆炸的可能,且控制方法未对反馈信号进行处理,实际使用中发现信号扰动较多,易造成执行器过多的不必要主动控制动作,会导致控制效果变差,浪费有限船载电能,缩短续航里程。文献[15]采取了PD控制对航迹跟踪,由于陆地行驶车辆无风浪干扰,PD控制对于陆地行走的车辆跟踪效果较好,对于受风浪不断干扰的明轮船而言,跟踪效果较差。因此,克服扰动对航迹跟踪的影响、降低控制运算量、提高系统稳定性是明轮船航迹跟踪研究的关键[16]。针对实际状况,本文提出一种运算量较小的基于卡尔曼滤波的离散滑模控制方法实现明轮船的直线跟踪。
1 航迹跟踪系统建模
明轮船的航迹跟踪属于欠驱动水面运动系统。采用船舶运动坐标系,其运动方程[9-10,17]为
(1)
其中
ν=[vr]T
式中m——明轮船质量,kg
xG——明轮船重心坐标,m
u0——明轮船航行速度,m/s
Iz——明轮船质量对z轴的惯性矩,kg·m2
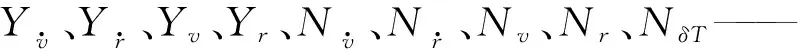
v——横漂速度,m/s
r——转艏角速度,(°)/s
δR——明轮船虚舵角,(°)
航迹跟踪的核心是控制明轮船的船艏航向。通过调整艏摇角使明轮船的航迹偏差不断得到纠正。根据文献[9-10],船舶运动时呈现非常大的惯性,因提供给明轮船控制船艏运动方向的能量有限,通常角速度低于3(°)/s,船舶运动具有低频特征,可以描述为一阶微分方程。在忽略横漂速度v的基础上,采取野本一阶模型(Nomoto)的形式[17-19],给出明轮船的艏摇角速度系统传递函数为
(2)
其中
det(N(u0))=Yv(Nr-mxGu0)-Nv(Yr-mu0)
式中n11、n21——明轮船附加质量水动力系数
b1、b2——明轮船转艏水动力系数
T——稳定性系数
K——回转性系数
2 船艏运动的离散滑模控制
滑模变结构控制策略可以使系统“结构”具有随时间变化的开关特性。迫使系统沿着规定轨迹作高频、小幅运动实现滑动模态。离散滑模控制是滑模控制数字化方式[20-21]。滑模控制器设计如下。
首先将艏摇角运动传递函数转换为状态方程并离散化,得到离散艏摇角运动状态方程
x(k+1)=Ax(k)+Bu(k)
(3)
式中A——状态矩阵B——输入矩阵
x(k+1)、x(k)——系统在k+1、k时刻的状态
u(k)——系统在k时刻的输入量
设计切换函数为
s(k)=Cex(k)
(4)
式中Ce——控制参数

s(k+1)=s(k)=Cex(k+1)=CeAx(k)+CeBu(k)
(5)
根据文献[20],设计离散滑模控制器u(k)为
u(k)=ueq(k)+FDx(k)
(6)
其中
ueq(k)=-(CeB)-1Ce(A-I)x(k)
(7)
FD=[f1f2…fn]
式中f1、f2、…、fn表示系统各状态变量的增益,I表示单位矩阵。
根据文献[20],定义Lyapunov函数为
(8)
由式(5)~(7)得到
s(k+1)=CeAx(k)-Ce(A-I)x(k)+CeBFDx(k)=
Cex(k)+CeBFDx(k)=s(k)+CeBFDx(k)
s2(k+1)-s2(k)=2s(k)CeBFDx(k)+
(CeBFDx(k))2
(9)
根据Lyapunov稳定性定理,s(k)=0为全局稳定平衡面,任意初始位置的状态都会趋向切换面s(k)。取到达条件为
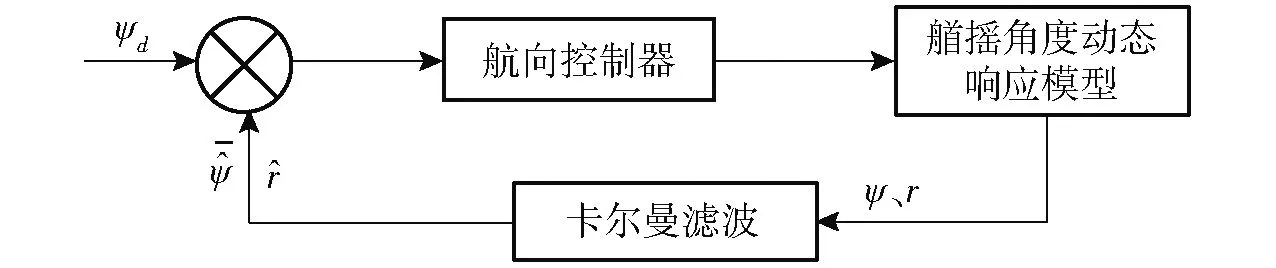
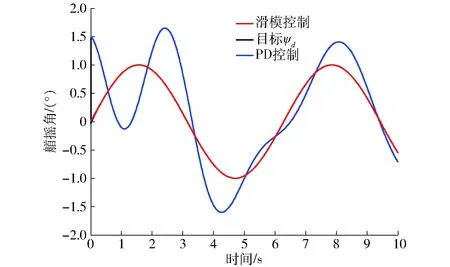
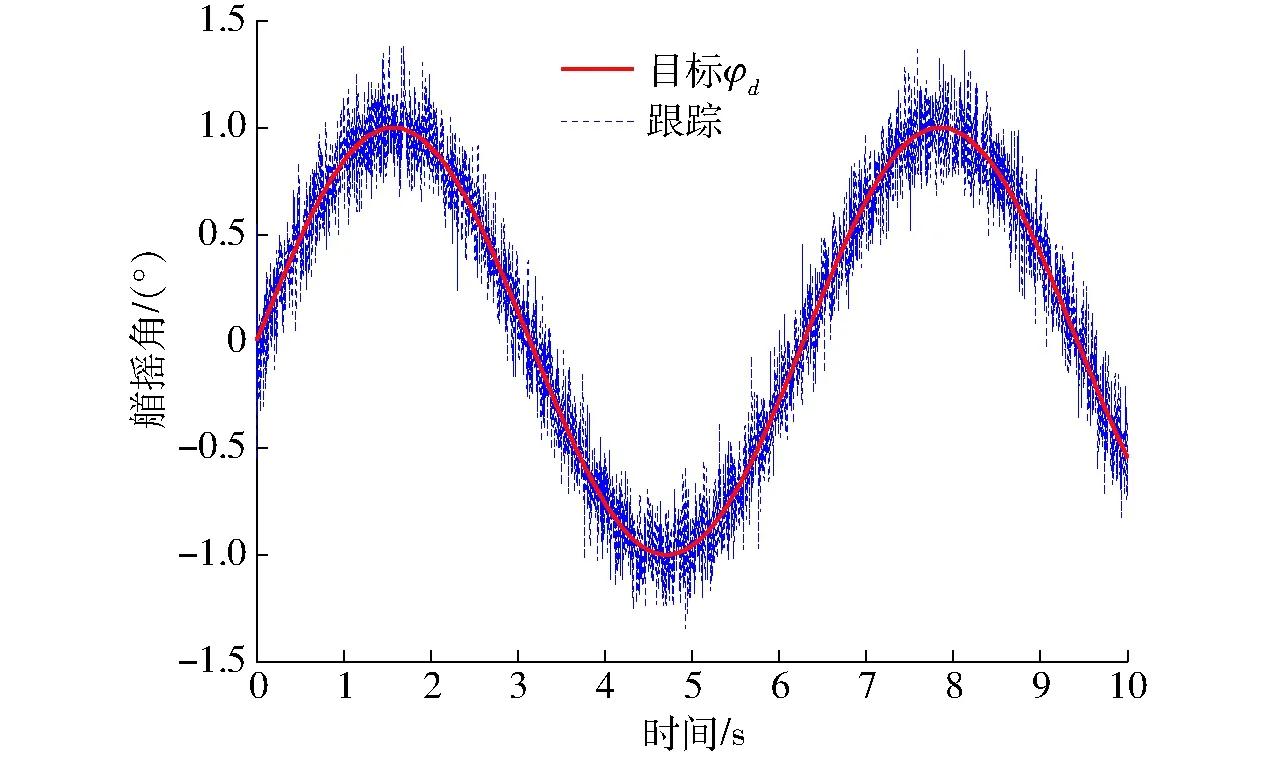
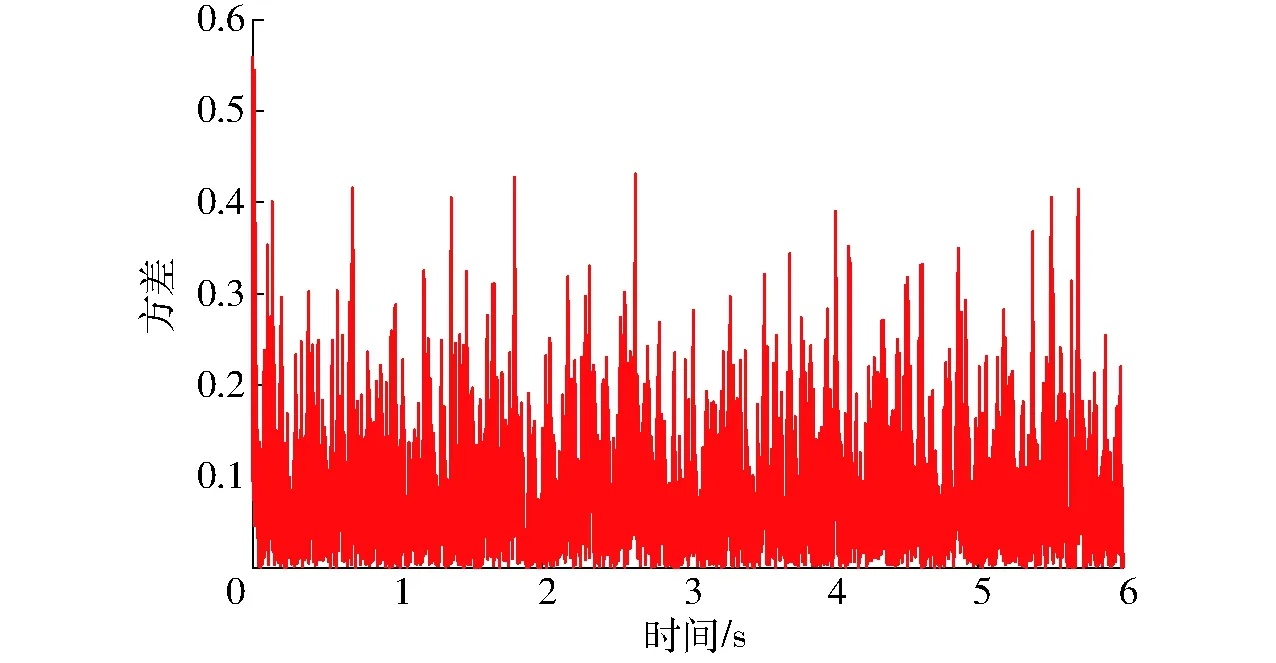
s2(k+1) (10) 则由式(9)可得 (CeBFDx(k))2<-2s(k)CeBFDx(k) 即 取|fi|=f0,f0>0,则对于每一个i,有 (11) 定义 (12) 将式(12)代入式(11)得到 (13) 可得 (14) 即 (15) 只要满足式(15)即可满足条件式(10)。 由式(12)和式(15)得 即 (16) 满足式(16)条件,确定f0。 综上所述,离散滑模控制率为式(6)、(7)、(16),即 (17) 则系统稳定。 明轮船在航行过程中不断受到风、波浪的干扰,船艏的艏摇角度始终处于小幅波动状态。文献[18]认为风浪对船舶航行的干扰主要由周期为5~20 s的长波叠加组成。部分二阶波引起的振荡可以通过自动航向纠偏抵消,而一阶波形引起的振荡和运动超出了自动驾驶仪的工作频带,会引起自动驾驶设备的高频运动,需要通过滤波的方式降低一阶波形的干扰。 船舶运动控制采取的滤波的方式主要有低通滤波、带通滤波、级联陷波滤波、基于观测器的滤波器等。虽然前述滤波可以降低风浪造成的干扰振荡,但是存在“相位滞后”的问题。经仿真、实际使用,发现此“相位滞后”极易引发系统振荡,造成航行的不稳定。 卡尔曼滤波能够从噪声污染的测量信号中,采用递归方式估计动态系统的真实状态,有效地避免了“相位滞后”。在雷达、通讯、导航、目标跟踪领域被广泛使用。若系统离散状态方程为[14,17] (18) 式中X——系统状态矩阵 Φ——系统矩阵 H——观测矩阵Y——系统输出 W(k)——输入噪声 Z(k)——观测噪声 Γ——噪声驱动矩阵 其卡尔曼滤波增益的计算过程为: (1)状态一步预测 (k+1|k)=Φ(k|k) (2)状态更新 (k+1|k+1)=(k+1|k)+Ka(k+1)ε(k+1) 其中 ε(k+1)=Y(k+1)-H(k+1|k) 式中ε——系统实际输出与观测估计输出的误差 Ka——卡尔曼滤波增益 (3)滤波增益矩阵 Ka(k+1)=P(k+1|k)HT(HP(k+1|k)HT+R)-1 式中P——协方差矩阵R——Z(k)的方差 (4)一步预测协方差矩阵 P(k+1|k)=ΦP(k|k)ΦTΓQΓT 式中Q——W(k)的方差 (5)协方差阵更新 P(k+1|k+1)=(In-Ka(k+1)H)P(k+1|k) 式中In——单位对角阵 初始条件 式中μ0——系统状态初始值 P0——协方差矩阵初始值 卡尔曼滤波将系统模型引入滤波过程,通过状态估计方差计算卡尔曼增益,反复迭代得到最优状态估计。且由于离散卡尔曼滤波不需要存储大量历史数据,适合计算机工作。明轮船的航迹跟踪和航向保持需使用二维卡尔曼滤波,故对艏摇角及艏摇角速度进行二维滤波。 明轮船艏摇角跟踪控制系统的结构如图1所示。 图1 艏摇角跟踪控制系统Fig.1 Yaw angle tracking control system 电子罗经和惯性导航设备给出明轮船当前航向角ψ、艏摇角速度r,经卡尔曼滤波后进行负反馈,得到滤波降噪后的当前航向角、艏摇角速度,航向控制器根据给出的目标航向角ψd,结合负反馈信号进行计算、经过左右明轮转速分配器分配后,得到左右明轮的各自转速nl和nr。左右电动机转速控制器根据给定的左右明轮的各自转速nl和nr,给出驱动左右电动机的信号ul和ur驱动电动机。电动机的转速信号n1、n2经负反馈,形成转速闭环控制。据此推转左右明轮,驱动船体运动。 为验证算法有效性,使用Matlab软件进行计算机仿真测试。根据明轮船的试验艇参数,建立明轮船艏摇角动态响应模型[10]。根据控制系统结构建立明轮船艏摇角仿真系统,如图2所示。 图2 明轮船艏摇角仿真系统Fig.2 Paddle wheel ship yaw angle simulation system 根据上述仿真系统结构,将仿真程序输入Matlab计算机软件系统进行动态响应仿真,得到仿真结果。仿真过程中,使用正弦信号作为跟踪目标信号。对控制系统跟踪信号不仅有位置误差的要求,还有速度误差的限制。不施加干扰时的跟踪效果如图3所示。 图3 无干扰跟踪效果Fig.3 Tracking effect without interference 图3显示了明轮船船艏采用滑模控制方式与采取纯PD控制方式时船艏对目标偏航角的跟踪效果,二者差距显著。两种控制方式的初始状态角度是1.5°。跟踪目标信号是从0°开始的正弦信号。仿真结果显示离散滑模控制能够快速跟踪目标信号。由于滑模算法的快速跟踪特性,使得采取滑模算法时,控制信号在初始阶段存在短时间的过饱和现象,可以通过限制控制信号输出幅值的方式进行消减。PD控制对目标的跟踪是逐步逼近,振荡收敛,实现最终的跟踪效果慢了许多。 抗干扰检验时,在仿真系统的输出信号上施加无量纲高斯噪声信号,得到在干扰下的艏摇角跟踪仿真结果,如图4、5所示。 图4 有干扰跟踪仿真结果Fig.4 Tracking effect with interference 图5 有干扰跟踪仿真方差Fig.5 Interference tracking simulation variance 仿真结果表明:离散滑模控制在高斯噪声干扰作用下,依然可以控制船艏进行航向跟踪,但是跟踪过程谐波较大,有干扰无滤波跟踪结果与目标信号的无量纲方差达到0.4。可以预见干扰会导致欠驱动系统明轮船艏做出幅度较大、频率较高的频繁控制动作。这对明轮船驱动设备、续航时间都会产生不利影响。 引入卡尔曼滤波降噪后的仿真结果表明,施加相同量级的高斯噪声干扰,跟踪信号的谐波幅值大幅度降低,如图6、7所示。 图6 有干扰滤波跟踪仿真结果Fig.6 Interference filter tracking simulation results 图7 有干扰滤波跟踪仿真方差Fig.7 Interference filtering tracking simulation variance 经数据分析,在加入卡尔曼滤波之后,跟踪信号与目标信号的无量纲方差降低到0.18。显然,卡尔曼滤波的引入,对干扰起到了抑制与降低。这对于明轮船延长续航时间、降低控制系统不必要的高频动作作用明显。 为验证算法的可行性,采用实际样船进行算法适航性验证。经测量获取明轮船参数,计算相关水动力参数。试验明轮船见图8。 图8 明轮船样船Fig.8 Paddle wheel ship 将离散滑模算法的控制代码输入控制系统,并反复进行调试、试验。试验当天多云,风力3~4级,气温15~24℃。得到转艏运动试验动态响应结果如图9所示。 图9 转艏动态响应曲线Fig.9 Dynamic response curves 试验曲线显示了明轮船转艏运动、直线运动的艏摇角动态变化过程。开始阶段是转艏运动,艏摇角急速拉升。经图9的试验结果分析,离散滑模控制方式下偏航角的最大超调量较PD控制方式减小25%,调整时间减少50%。受制于明轮船转艏运动过程的艏摇角速度限幅和执行电机输出饱和限制的影响,转艏运动的快速性、超调量不及仿真效果,但是明轮船的直线跟踪效果达到预期,直线跟踪偏差效果见图10。 图10 明轮船直线跟踪偏差Fig.10 Paddle wheel ship linear tracking deviation 从图10可见,明轮船进入直线轨迹跟踪时,由于转艏运动,跟踪轨迹切换造成跟踪目标不定,致使明轮船刚进入直线段航迹点时出现较大偏差。随后,明轮船完全进入直线段目标轨迹区域航行,由于引入卡尔曼滤波滑模算法,直线跟踪偏差均在10 cm以内,达到直线跟踪目标要求。由于跟踪过程存在阵风干扰,明轮船被风力推向偏航。设计的滤波滑模控制算法进行了纠偏操作,使明轮船沿着目标轨迹航行。分析图10的试验数据,离散滑模控制实现的明轮船直线航迹在刚进入直线段时,快速逼近目标轨迹,在风浪干扰的作用下,最大偏差只是瞬间超过10 cm,其他时间段均低于10 cm,远优于PD控制实现的效果。 无风浪干扰时,无卡尔曼滤波PD控制算法的跟踪精度虽然满足要求,但是收敛速度较慢。当出现风浪干扰时,明轮船出现较大的偏航,在无滤波的PD控制算法作用下,最终也能纠偏,但是航行过程的波动较大,最大偏差达到0.35 m,收敛到满足偏差要求的航迹时间也较长。实际航行试验表现为在目标航迹附近多次振荡。 有卡尔曼滤波的滑模航迹跟踪控制算法,在跟踪精度满足要求时,跟踪过程更加平稳,收敛速度更快。这对于明轮船工作过程的稳定性、节能降耗、延长续航时间起到重要作用。 (1)采用离散滑模控制方式对明轮船的转艏运动进行控制。通过建立转艏运动模型,进行了离散滑模控制仿真,证明离散滑模算法可以对明轮船的转艏运动、直线跟踪进行有效控制。 (2)对干扰采取了卡尔曼滤波进行消减。仿真结果说明,卡尔曼滤波可以有效抑制航行过程中风力、波浪对航迹跟踪造成的干扰,对提升系统控制过程的平稳、节能降耗、延长续航起到重要作用。 (3)对算法进行了试验验证。转艏运动在算法控制下,均能实现直线跟踪。结果表明,采取基于卡尔曼滤波的滑模控制方式较PD控制,艏摇角的最大超调量比PD控制方式减小25%,调整时间减少50%,航迹偏差低于10 cm。由于转艏运动的角速度限幅、执行电机的饱和特性限制,明轮船的大角度转艏动态响应特性不及仿真效果,但目标轨迹跟踪效果达到预期。
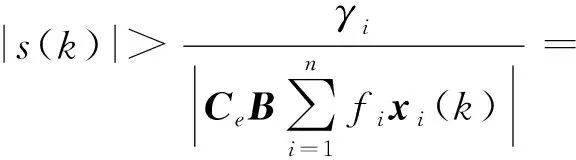
3 卡尔曼滤波
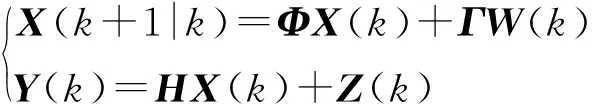
4 控制系统结构设计与仿真



5 试验



6 结论

