具有不可微时变时滞四元数神经网络的全局μ-稳定性*

刘丽缤, 游星星, 潘和平**

(1.重庆工商大学 财政金融学院,重庆400067；2.重庆交通大学 经济与管理学院，重庆 400074)

0 引 言

20世纪80年代，自美国加州理工学院生物物理学家Hopfield提出人工神经网络系统以来，人工神经网络得到了广泛研究[1].目前，人工神经网络已广泛应用于信号处理、模式识别、联想记忆、优化计算等诸多领域[2-3].在这些领域的应用中，首要问题是分析网络的稳定性[4-5].

根据神经网络处理数据的类型，可以将其分为实值神经网络(RVNNs)、复值神经网络(CVNNs)和四元数神经网络(QVNNs)3类.目前关于实值、复值神经网络稳定性的研究已经有很多成果[5-7]，但它们具有局限性.QVNNs作为RVNNs和CVNNs的扩展，其神经元的状态、输出以及网络的权值都是四元数，在处理高维度数据时，具有很大优势，比如图形处理、3D仿射变化.因此，对四元数域上神经网络的动力学行为分析成为近年来的研究热点.Liu Y[7]通过四元数复数分解法，将QVNNs分解为两个复值系统，利用同胚映射原理，得到网络平衡点的全局μ-稳定性判据，其结果是以复值线性矩阵不等式(CVLMI)形式表示的.文献[8—9]采用类似于文献[7]的方法，将QVNNs系统分解，得到了具有混合时滞QVNNs系统平衡点的存在性、唯一性、全局μ-稳定性的充分条件.Chen X F[10]基于同胚映射原理和Lyapunov定理，利用四元数模不等式技术研究了具有泄漏、离散时滞和参数不确定的QVNNs系统的鲁棒稳定性.上面提到的关于μ-稳定性的结果大多都是在QVNNs的激活函数可分解的条件下得到的，这种分解的方法使得系统的维度成倍增加，并且会增加计算的复杂度.此外，由于四元数乘法不满足交换性，将QVNNs分解为两个CVNNs的方法不具有普适性.

基于以上分析，在不要求QVNNs可分解情况下，构造Lyapunov-Krasovskii泛函，通过自由权矩阵和矩阵不等式等技术，将QVNNs考虑为一个整体，研究了具有不可微时变时滞的四元数神经网络的全局μ-稳定性,获得了网络平衡点的全局μ-稳定性的充分性判据.

结构组织如下：第1节介绍了相关预备知识，包括四元数代数、系统介绍、假设、定义和引理；第2节给出了基本定理及μ-稳定性证明过程；第3节给出了一个数值算例验证了所得结果的有效性；第4节总结了文章所做的工作.

1 预备知识

1.1 四元数代数

一个四元数可以写成以下形式:

p=p0+p1i+p2j+p3k∈Q

其中p0,p1,p2,p3∈R，且虚数单位i,j,k满足i2=j2=k2=ijk=-1，ij=-ji=k，ik=-ki=j，jk=-kj=i，由此可知四元数乘法不可交换.定义另外一个四元数q=q0+q1i+q2j+q3k，则四元数p与q的和、乘积分别定义为

p+q=(p0+q0)+(p1+q1)i+(p2+q2)j+(p3+q3)k

pq=(p0q0-p1q1-p2q2-p3q3)+(p0q1+p1q0+p2q3-p3q2)i+

(p0q2+p2q0+p3q1-p1q3)j+(p0q3+p3q0+p1q2-p2q1)k

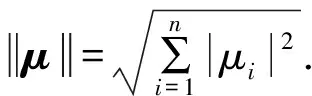
1.2 系统表示及基本引理

本文考虑如下具有时变时滞QVNNs系统:

(1)

式(1)中，z(t)=(z1(t),z2(t),…,zn(t))T∈Qn,表示神经元状态向量；自反馈连接权矩阵D=diag(d1,d2,…,dn)∈Rn×n且di>0，(i=1,2,…,n)；连接权矩阵、离散时变时滞连接权矩阵分别为A=(aij)n×n∈Qn×n，B=(bij)n×n∈Qn×n；f(z(t))=(f1(z1(t)),f2(z2(t)),…,fn(zn(t)))T为向量值激活函数；f(z(t-τ(t)))=(f1(z1(t-τ(t))),f2(z2(t-τ(t))),…,fn(zn(t-τ(t))))T∈Qn为具有时间延迟的向量值激活函数；外部输入向量为I=(I1,I2,…,In)T∈Qn；0≤τ(t)≤τ表示不可微分的离散时变时滞.

给出如下假设：

(H1)激活函数fi(·)满足Lipschitz条件，即对任意β1,β2∈Q，存在li∈R(i=1,2,…,n)，使得:

|fi(β1)-fi(β2)|≤li|β1-β2|

其中:li为常数，且Γ=diag(l1,l2,…,ln).

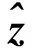
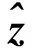
(2)

其中

定义2[9]若μ(t)>0是一个连续函数，当t→∞时，μ(t)→∞,存在常数K>0使得

成立，则式(2)是μ-稳定的.

引理1[9]对任意一个正定Hermitian常数矩阵W∈Qn×n，W≤0和标量函数α：[t,ξ]→Qn,t≤ξ，有

注1 T和*分别表示矩阵的转置和共轭转置；P≥Q(P>Q)表示矩阵是半正定(或正定)的；λmax(P)、λmin(P)分别表示矩阵P的最大、最小特征值.

2 主要结果

定理1 在假设(H1)成立的条件下，如果存在常数α,β≥0，正定的Hermitian矩阵P，对角矩阵R1,R2>0，四元数矩阵X11,X12,X13,X22,X23,X33,Q1,Q2，μ(t)>0是可微函数，使得不等式

(3)

(4)

成立，其中

则式(1)的平衡点是全局μ-稳定的.

证明构造Lyapunov-Krasovskii泛函

V(t)=V1(t)+V2(t)+V3(t)

(5)

其中:

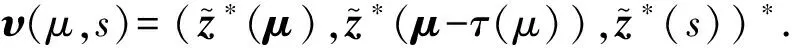
根据引理1，沿着式(2)求导可得：

(6)

(7)

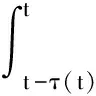
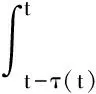
(8)

由假设(H1)可得：

(9)

(10)

根据式(2)，运用自由权矩阵，令

(11)

将式(6)—式(11)相加可得

D+V(t)≤μ2(t)η*(t)Ωη(t)

(12)

其中：

(t-τ(t))))*

由式(4)可得：

D+V(t)<0,t≥0

(13)

由于λmin(P)是一个实数,因此可得到:

所以

(14)

其中:

故式(1)的平衡点是全局μ-稳定的，证毕.

注2 近年来，许多学者致力于QVNNs系统的稳定性研究，但由于四元数乘法不满足交换律，使得研究四元数比实数、复数更为复杂.文献[7,8]将QVNNs系统分解为两个CVNNs，研究了在时变时滞可微情况下QVNNs系统的全局μ-稳定性；文献[9]采用类似的分解方法研究了不可微时变时滞QVNNs系统的全局μ-稳定性，但这种分解方法会导致两个问题：一是会使系统维数增加导致计算更复杂，同时还会丢失一些与四元数所携带振幅、相位相关的信息；二是在系统激活函数不可分解时，这种方法获得的结果往往是无效的.因此，本文将QVNNS系统考虑为一个整体，研究了不可微分时变时滞QVNNs系统的全局μ-稳定性，在一定程度上扩展和改进了文献[7-9]的结果.

3 数值仿真实例

本文考虑如下具有两个神经元的不可微分时变时滞的QVNNs系统：

(15)

f1(z)=f2(z)=0.5 tan h(z),∀z∈Qτ(t)=

0.2|sin (3t)|

D=diag(2.881,0.963)

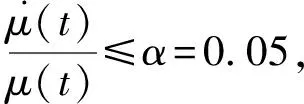
运用MATLAB YAMIP工具箱，可以求解式(3)和式(4)，得:

由定理1知式(15)的平衡点是全局μ-稳定的，状态变量的时间响应轨线图(图1—图4)验证了平衡点的全局μ-稳定性，并且式(15)的初始条件为

z1(t)=6.162+1.259 i-0.229 j-2.619 k

z2(t)=-3.081-1.298 i+0.963 j+4.942 k

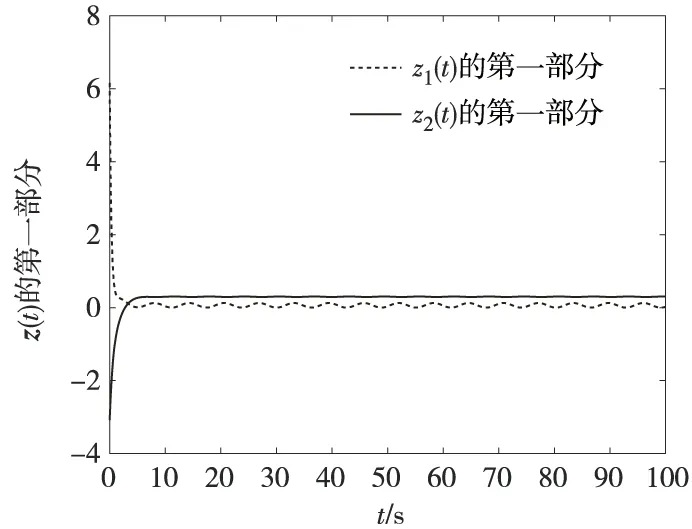
图1 第一部分时间响应轨线

图2 第二部分时间响应轨线

图3 第三部分时间响应轨线

图4 第四部分时间响应轨线

4 结 论

研究了具有不可微分时变时滞的QVNNs系统的全局μ-稳定性，在不要求QVNNs系统可分解的情况下，构造合适的Lyapunov-Krasovskii泛函，通过自由权矩阵和矩阵不等式等技术，获得了系统平衡点的全局μ-稳定性的充分性判据；最后，通过一个数值仿真实例验证了结果的有效性.