一种基于Hebb优化准则的扩频码序列识别方法*
熊 刚,赵尔凡
(中国电子科技集团公司第30研究所,四川 成都 610041)
0 引 言
直接序列扩频通信(Direct Sequence Spread Spectrum,DSSS)技术由于具有较好的抗干扰性、高通信速率、易于实现码分多址和隐蔽性强等特点,已被广泛运用于军事通信、民用通信和导航领域[1],如GPS导航系统、通信电台、移动通信CDMA、WCDMA和WiFi中IEEE 802.11b标准等。扩频通信中的扩频码一般采用伪随机序列与待传输信息进行模二相加,使得调制信号的频谱得以扩展。单位带宽上的功率很小,即信号的功率谱密度很低,因此外界很难截获传送的信息。在非合作通信条件下实现对直接序列扩频信号的扩频码序列识别,是后续成功解扩接收信息的前提,对认知无线电、频谱监测以及网络安全分析等领域具有重要意义。扩频码序列识别在缺少先验知识的情况下进行,具有较大难度。
传统方法是通过基于特征值分解(Eigen Value Decomposition,EVD)的方法对信号扩频码开展识别和分析,计算量较大,易受噪声影响,在低信噪比条件下性能不理想。在常见的基于特征值分解的算法中,接收到的直接序列扩频信号样本点根据非重叠的时间窗口进行划分,窗长度为扩频码周期,然后计算自相关矩阵的特征矢量和特征值。经证明,通过最大两个特征值和特征矢量可正确识别出扩频码序列。这种算法的缺点是计算复杂度较高,且由于需要精确获取扩频码起始位置,在实际应用中有较大局限性,不适合工程实现。此外,采用长序列扩频的直接序列扩频信号伪码周期较长,接收端通常无法收到一个完整周期的序列,且一个伪码周期内包含多个信息码元,传统方法包括基于特征值子空间分解的算法[2],对长序列的识别性能较差,需要采集较多的信号样本点,计算处理量大,在很多实际场合中容易失效。例如,Frobenius范数法等利用短码信号的结构,因而不能用于长序列直接序列扩频信号。对于扩频码盲同步处理而言,在实际直接序列扩频通信如CDMA系统中,用户扩频码不可能完全正交,且在传输过程中,恶劣的信道也会使得扩频码的正交性严重恶化,必然会产生多址干扰、远近效应和多径效应,使得第三方在截获过程中获取用户信号同步的难度进一步加大3]。为解决上述问题,本文提出了一种基于Hebb规则优化的扩频码序列识别与同步方法,在低信噪比的复杂电磁环境中性能优于传统方法。
1 信号模型分析
典型的直接序列扩频信号发射和接收系统原理,如图1所示。

图1 直接序列扩频信号处理模型
接收到并经过信号采集样本后的直接序列扩频信号计算定义式为:

其中,{d(kTc)}代表原始数据符号,{c(kTc)}表示扩频码序列的离散信号采集样本点计算定义式,Tc为各信号采集样本点的时间间隔,S代表信号能量,{n(kTc)}表示零均值、方差为σ2的高斯白噪声。为了表述方便,以下用{c1,…,cN},ci∈{±1}表示扩频码序列,且di表示第i个传输的BPSK调制信息符号,di∈{±1}。实际中,通常选取伪随机PN序列作为扩频码序列。扩频前的信噪比可表示为:

扩频码序列识别的作用即为从截获的信号序列{rk}中识别得到 {c1,…,cN}。
2 算法分析和改进
本文提出了一种扩频码序列识别和同步方法,采用基于Hebb规则的优化思路和长序列区间并行计算模型,从而成功估计出长序列、短码扩频序列。新方法中进行特征矩阵维数的化简处理,并分析完成了对扩频码的盲同步处理。
短码扩频模型——在扩频周期内仅调制一位信息码元,基带模型可表示为:

其中,ai表示信息符号的序列,{ai=±1},A表示信号幅度,Ts表示符号周期,n(t)表示方差为σn2的高斯白噪声。P表示扩频码序列长度,信息符号的波形可表示为:

且有:

式(5)中,ck表示扩频码序列,{ck=±1,k=0,…,P-1},Tc为码周期,pc(t)表示传输信道及滤波器的响应,h(t)表示扩频码序列与信道响应的卷积。基带数据波形一般为矩形脉冲形式。
长序列扩频模型——对应于每个扩频周期内调制多个信息码元,其基带模型可表示为:

其中,dk代表独立同分布的数据信息序列,n(t)表示高斯白噪声变量,Ts表示数据符号的周期,cu(u=0,1,…,KN-1)表示扩频长序列序列的第u个码元,Tc表示码元宽度且Tc=Ts/N,N表示扩频长序列序列对应于数据符号的划分长度。将接收到的LN个扩频码元分成L部分,因此每部分都包含了一个完整的伪码周期。根据传统准则,可得出:

其中f(r|c)表示接收信号的条件概率分布函数,c^指的是待估计的扩频码序列。扩频信号数据特征矢量d是随机的,用r(n)和d(n)分别表示在第n部分符号中的接收和发送的数据符号。对于直接序列扩频QPSK调制信号,将d进行平均处理,得到:

其中cosh表示偶函数。
扩频码序列识别方法对于非合作情况下的直接序列扩频信号处理具有重要意义[4]。直接序列扩频信号非合作接收系统的原理,如图2所示。
本文采用对Hebb规则优化后的识别思路进一步简化运算,以期达到良好性能。基于Hebb规则的识别估计器实质是一种自适应FIR滤波器,通过对计算进行改进,可以得到扩频码相关矩阵主要分量特征矢量,且优化后的估计器结构简单,易于实现。各扩频码符号对应的权因子计算定义式为:


图2 对直接序列扩频信号非合作接收系统
其中,η代表步长因子,wi表示第i个权因子矩阵元素,xi表示第i个输入信号采集样本点,且表示识别估计器的输出,y(n)wi(n)表示归一化的约束特征矢量部分。优化后Hebb权因子的更新可通过扩频码序列的输入-输出特征矢量矩阵相关函数完成计算。Hebb规则中的学习过程可由权特征矢量适当的引导,从而增强了扩频码序列输入-输出特征矢量矩阵的相关性。
式(9)中,权因子矩阵的更新项主要体现在乘积的符号而不是幅度,从而影响权值更新的方向。优化后的Hebb识别估计器权因子更新计算式为:
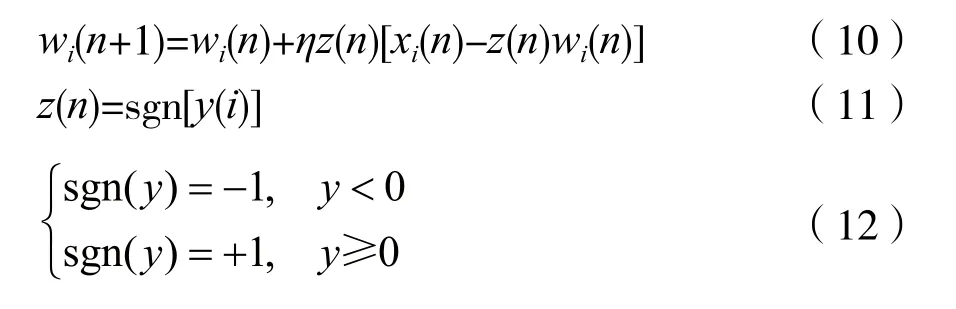
由于z(n)=±1,计算式还可进一步化简为:

通过采用最优估计器思路,可以实现计算量的简化,还能在一定程度上增加低信噪比时的估计精度。
基于本文的思路可实现符号矩阵的简化运算处理,同时对方法中第二步的乘法运算进行了优化。当进行空间搜索运算时,可使用和符号函数,即分别与±1相乘的处理技巧,以代替计算复杂度高的浮点乘法。在完成对c1的正确估计后,对c2可采取同样的处理流程。该识别估计方法可得到更高的估计准确性,对c2的计算定义式为:

3 仿真结果及性能分析
为了验证本文方法,采用MATLAB软件仿真得到性能曲线。试验依据实际移动通信系统应用中的CDMA2000标准,直接序列扩频信号信号采集样本率设为200 MHz,载波频率为70 MHz,以不同的初始偏置区分各用户,扩频码长215,仿真信道为抽头L=5的多径瑞利衰落信道,信道中的噪声是零均值的加性高斯噪声。仿真次数为1 000次,噪声为高斯白噪声,分别采用本文中的新算法和过去的基于传统准则的算法在不同的信噪比条件下进行仿真比较分析,并且使用扩频码的互相关因子对算法估计性能进行衡量。互相关因子即为盲估计算法推导得出的码序列与真实扩频码每个码元比较时,一致的数目与不同的数目之差。图3表示本文算法与传统算法的性能曲线,横轴代表信噪比,纵轴代表估计结果与真实码元的互相关因子。
从图3可以看出,在低信噪比环境中,本文的扩频码识别方法性能优于传统算法。在信噪比为-2 dB左右时,互相关因子为1,即能够在低信噪比条件下正确估计扩频码序列,是一种性能优越的方法。

图4 新方法的同步估计正确概率曲线
图4表示本文方法在观测数据组数分别为N=200、250、300、400时的同步估计正确概率曲线,其中每种算法在各个信噪比点同步次数为1 000次。可以看出,当信号采集样本组数在250组以上,信噪比大于-10 dB的情况下,正确同步估计概率大于90%。
4 结 语
本文提出了一种基于Hebb规则优化的扩频码序列识别和同步方法的新方法,适用于多种情况,抗噪性能好。该方法具有计算量相对较小、数值稳定性好以及易于工程实现的优点。针对目前扩频信号盲同步方法效果不理想、运算处理复杂的问题,本文方法还设计了新型扩频码相关性度量函数作为最优同步点估计器,提高了算法效率,在低信噪比的复杂电磁环境中性能优于传统方法。综上所述,本文方法可以在认知无线电、频谱监测和网络安全分析等方面发挥重要作用。

