基于压缩感知的φ-OTDR系统信号处理*
郑 亮,乔小瑞,王瑛剑
(海军工程大学 电子工程学院,湖北 武汉 430000)
0 引 言
相位敏感光时域反射计(Phase-sensitive Optical Time Domain Reflectometer,φ-OTDR),是一种利用光纤中后向瑞利散射光的多光束干涉现象,进行振动定位与监测的光纤传感技术。由于其抗电磁干扰、灵敏度高、定位精确、数据处理相对简单等特点,特别适合执行长距离,大规模的监测任务。目前在大型建筑的健康监测,石油管道的安全监控,国家边界安全等领域得到了广泛的应用[1]。传统的φ-OTDR系统中,应用最成熟的信号处理方法是平均法,即对多次测量得到的多条散射信号进行累加平均处理,然后再对平均结果进行差分,这一方法能有效提高后向瑞利散射信号的信噪比。但是这种处理方法会大幅降低系统的最高频率响应范围,只可以用于定位,应用在进行振动监测的φ-OTDR系统中并不合适[2]。压缩感知理论[3],可以利用观测矩阵将高维信号投影到低维空间上,通过原信号所具有的稀疏特性,利用优化算法将原信号重构出来,这一过程不会改变信号的频谱范围。因此本文提出了一种基于压缩感知理论的信号处理方法,通过求光纤各点处的重构误差值来定位振动位置,并求出振动频率。这一方法可以在保证系统频率响应范围不变的同时提高系统的抗噪性能。
1 φ-OTDR系统概述
1976 年,Barnoski M.K.和 Jensen S.M.最早提出了光时域反射计(Optical Time Domain Reflectometer,OTDR)技术[4],这一技术问世40多年以来,被广泛应用于定位光纤线路中的断点及其它异常[5]。OTDR系统原理如图1所示,激光器产生的激光经声光调制器调制为光脉冲,经过环形器后输入到传感光纤中,光脉冲在光纤中会产生瑞利散射光,其中后向瑞利散射光会返回到发射端,通过光电探测器得到沿光纤分布的瑞利散射光强度曲线。当光纤上某点发生扰动或突变时,光纤相应位置处的折射率也会跟着变化从而造成后向瑞利散射光强度的改变,通过探测这一变化就可以对扰动进行定位。
OTDR本身具有分布式测量的特点,然而,当其用于分布式传感时,灵敏度却很低,因此,人们在传统OTDR的基础上发展出φ-OTDR技术。φ-OTDR的原理与OTDR类似,都是通过探测返回的瑞利散射光从而确定扰动位置。不同的是,φ-OTDR使用的激光光源是窄线宽的。由于瑞利散射属于弹性散射,散射光的频率与入射光相同,所以当入射光频率单一且稳定时,返回的后向瑞利散射光会产生多光束干涉效应。相干光对振动非常的敏感,微小的振动就可以造成相干光曲线强度的改变,所以相比传统OTDR系统,φ-OTDR的探测灵敏度有了极大的提高。
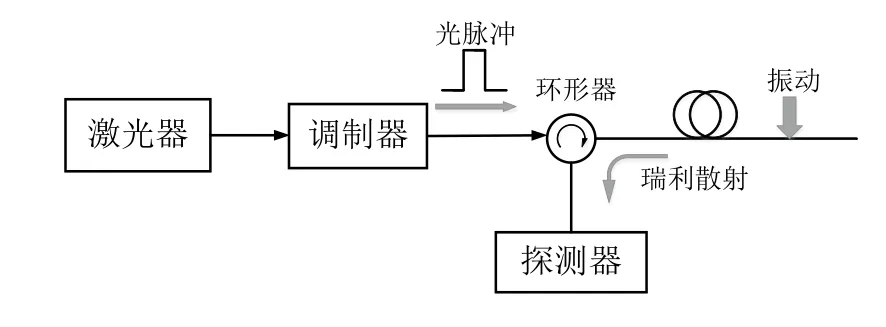
图1 OTDR系统原理图
φ-OTDR系统为了避免光信号之间的干涉串扰,在入射光脉冲产生的瑞利散射光全部返回到发射端之前,不允许发射下一个光脉冲。设两个入射光脉冲之间的时间间隔为τ,τ的最小值可等效的看作是光脉冲在光纤中往返所需要的时间,如式(1)[2],

其中L是光纤长度,vg是光的群速度。所以φ-OTDR系统发射探测脉冲的频率f存在极大值fmax=1/τmin,根据奈奎斯特采样定理,可得φ-OTDR系统的频率响应范围是0~0.5f,当光纤上的振动频率处在这一范围内时,可以在定位的同时求得振动频率。
2 基于平均法的信号处理方法
由于普通单模光纤中返回的瑞利散射光信号非常微弱,尤其在长距离的传感光纤中,非常容易被噪声淹没,因此需要特殊的信号处理方法来提高后向瑞利散射光的信噪比。对于φ-OTDR采集到的信号,通常我们使用平均法对其进行处理。
平均法中比较常见的有分离平均法[6]和移动平均法[7]。所谓分离平均法,就是将采样得到的N条瑞利散射曲线依照时间顺序等分为几组,各组分别进行平均处理,之后再进行差分叠加。例如,将1 024条瑞利散射曲线依照时间顺序等分为4组,每组256条做一次平均处理,可以得到四条平均曲线{x1,x2,x3,x4},对其执行操作xi+2-xi,并将结果叠加可以得到图2(a),从图中可以清晰的分辨出振源的位置。而移动平均法则是预先设置一个移动平均数m,在N条瑞利散射曲线上(N>m),通过沿时间轴不断步进的方式对每m条散射曲线求平均值,得到N-m+1条平均曲线,之后再通过移动差分的方式,得到信号处理图像。如图2(b),这是m=256时,1 024条瑞利散射曲线经移动平均法处理后得到的图像,由图易得振动位置在光纤1.6 km处。
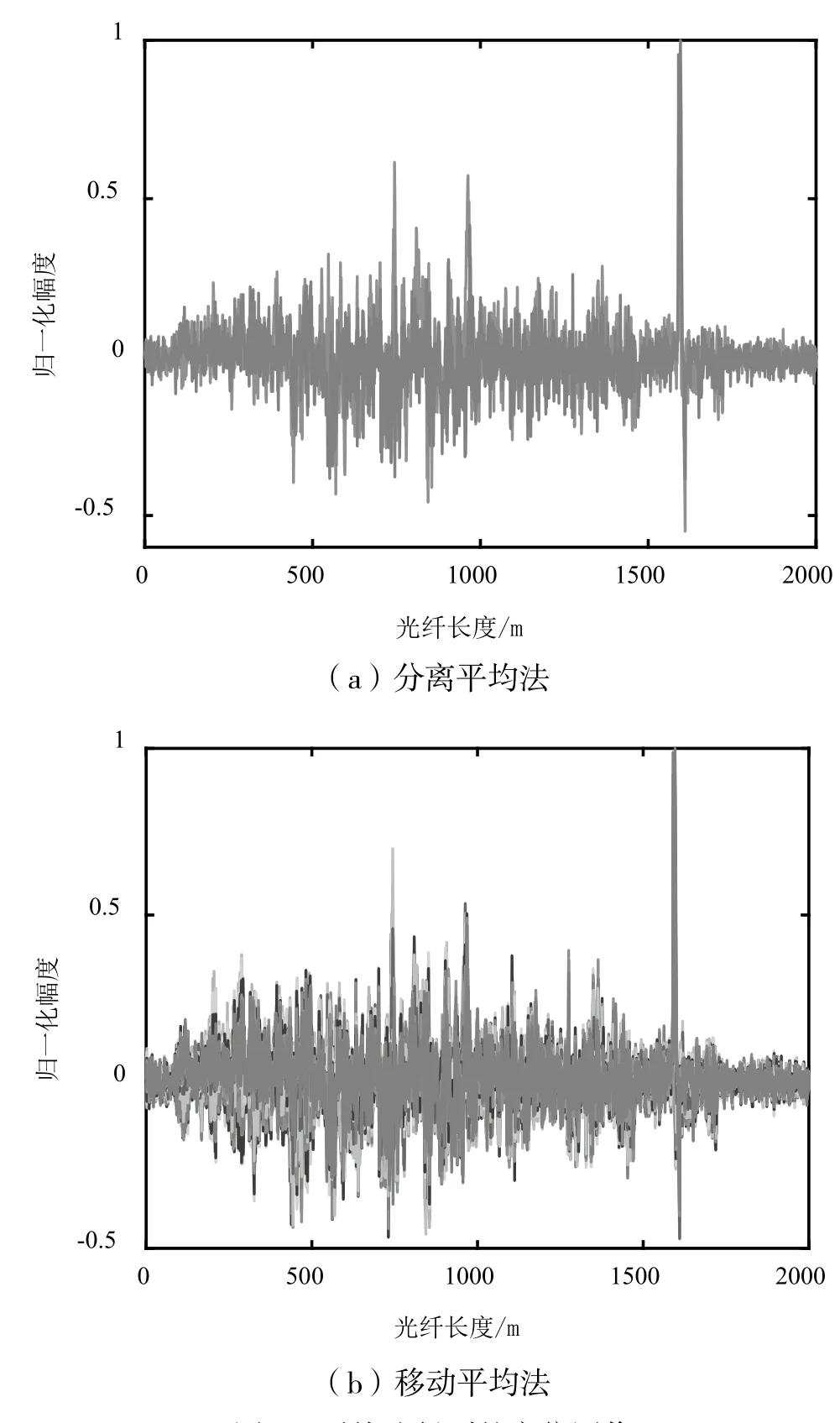
图2 平均法得到的定位图像
不论是分离平均法还是移动平均法,虽然可以降低信号噪声,求出振源位置,但是平均的过程相当于降低了系统的采样率,会相应缩小系统的频率响应范围,这显然不利于发挥φ-OTDR系统的性能。因此,本文提出使用压缩感知算法来进行信号处理,可以在降低噪声的同时维持原来的频率响应范围不变。
3 基于压缩感知的信号处理
3.1 压缩感知原理
2008年Donoho提出了压缩感知理论[8],这一理论证明,如果信号是稀疏的,那么它可以由远低于采样定理要求的采样点数重建恢复,具体原理如下。
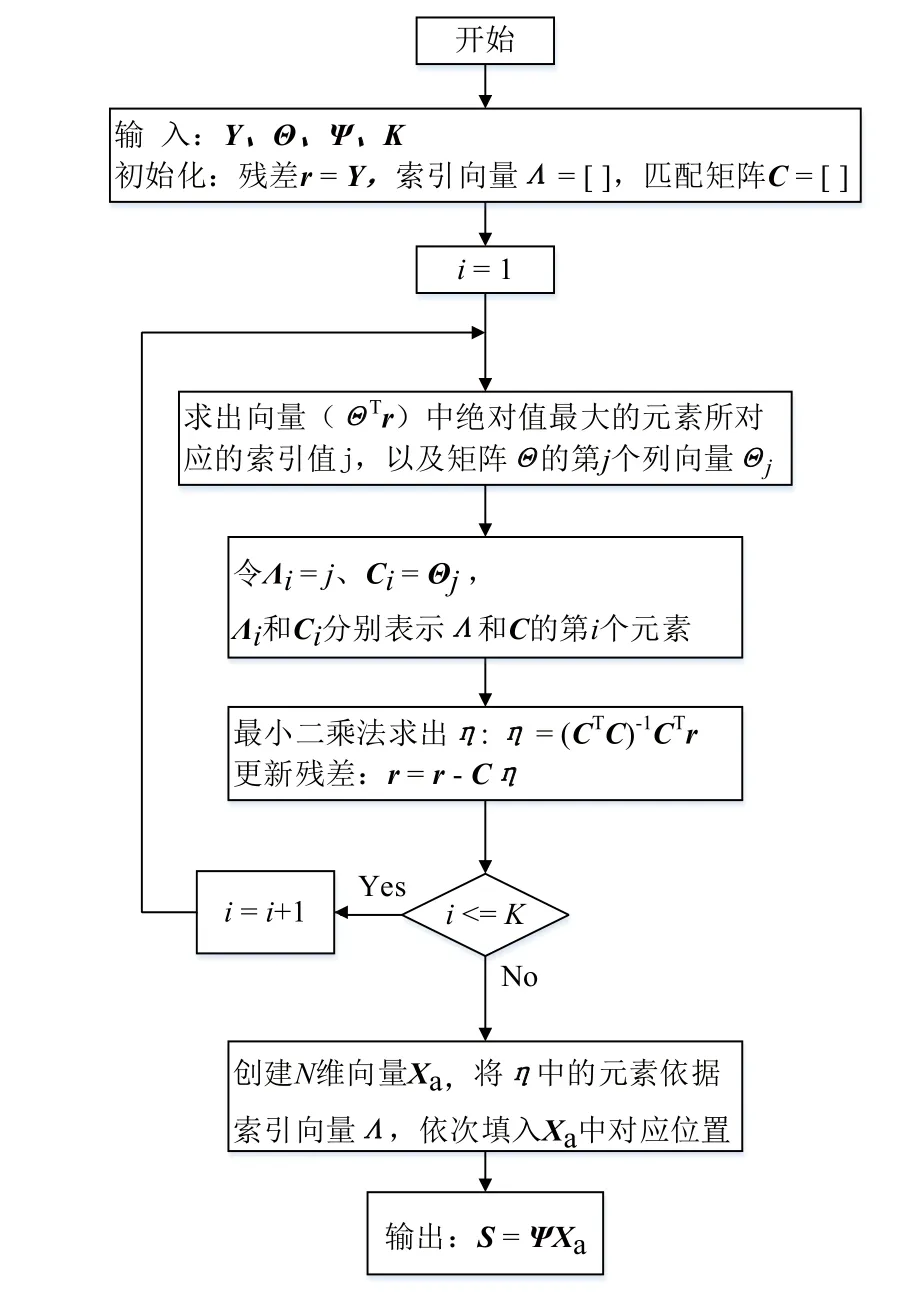
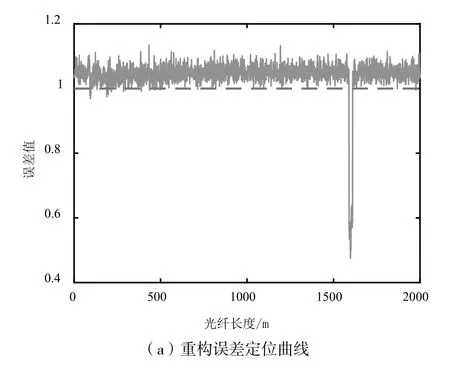
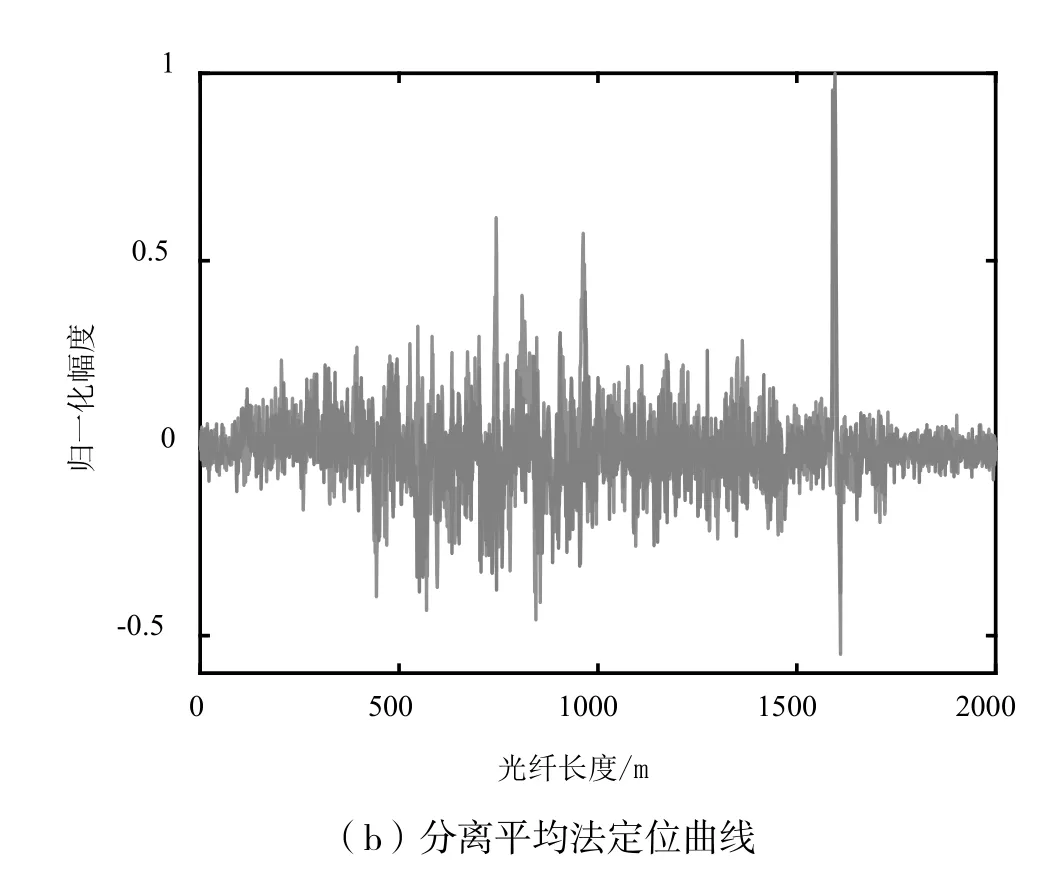
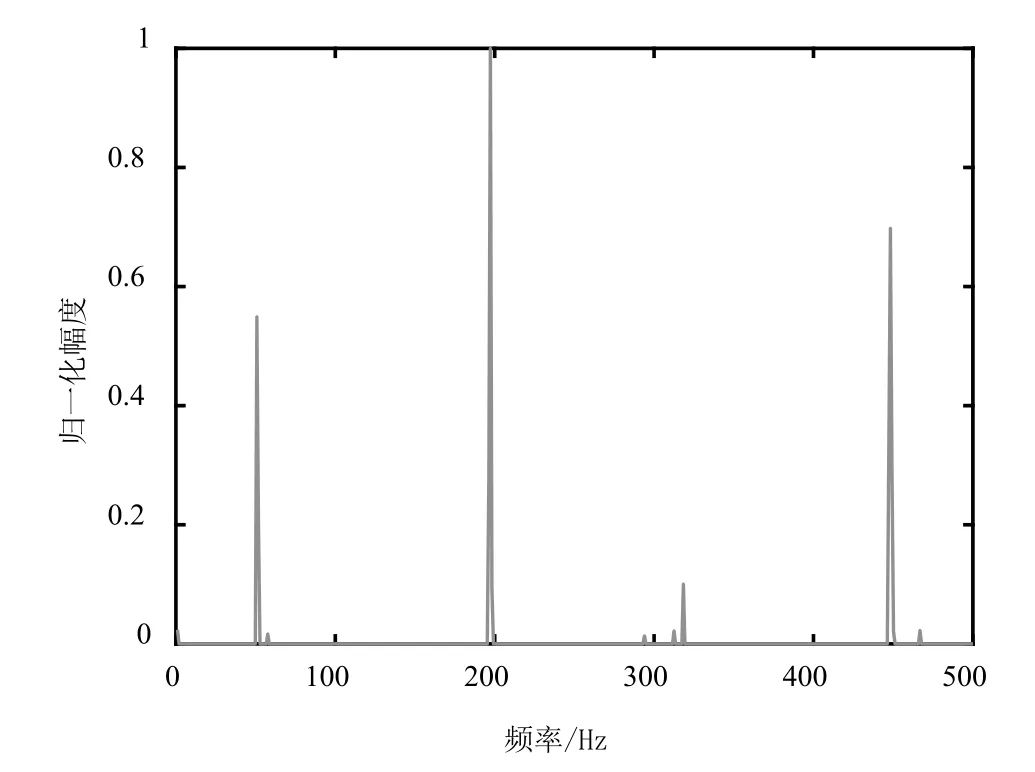
设一维向量S的长度是N,并且存在正交的空间变换矩阵Ψ使得S在这一空间的变换向量X是稀疏向量,即X中只有K个元素不为零,其余元素均为零,且K< 如果,现在已知Y和Φ,求S,因为Φ是M×N的矩阵,显然S的解并不唯一,但是如果存在空间变换矩阵Ψ,并且满足S=ΨX,带入式(2)可得: 此时问题转化为,已知Y、Φ和Ψ,在X的解集中,寻找一个含零元素最多的X,这时X有唯一解,进而可以求出S,这就是压缩感知的基本原理。其中,Y称为观测向量,矩阵Φ称为观测矩阵,Ψ称为稀疏矩阵,为简化表述,定义Θ=ΦΨ,Θ称为传感矩阵。 所以压缩感知问题的核心是寻找一种重构算法,求出稀疏度最高的。目前压缩感知重构算法大致分为两种:凸优化算法及贪婪算法[9],因为贪婪算法的计算复杂度低于凸优化算法,所以得到了更多的应用。而贪婪算法中常见的又有,自适应匹配追踪法(Sparsity Adaptive Matching Pursuit ,SAMP)[10]、正交匹配追踪法(Orthogonal Matching Pursuit,OMP)[11]等。本文使用的是OMP法,其基本原理为,求出传感矩阵Θ中和Y最为匹配的列向量,并利用最小二乘法估算出这一列向量对应的X中的元素,利用这一元素反推出Y的近似值,并更新残差。将这一过程迭代K次,就可以求出稀疏度为K的X,进而求出原信号S。OMP算法的流程图如图3所示。 具体到φ-OTDR中,若是连续采样得到N条瑞利散射曲线,则光纤上每一点在时域都可以做出一条由N个采样点构成的信号曲线。将此曲线看作是离散信号S(z),z表示光纤链路位置,设振源处z=a,则信号S(a)的频域信号X(a)可以近似的看作是振源的频域信号Xv(a)与噪声的频域信号γ之和,即: 这里的Ψ是离散傅里叶逆变换矩阵,由于振源处振动信号的频率带宽是有限的,且频谱能量远大于噪声,所以Xv可以近似的看作是稀疏向量。则这一问题转化为,求稀疏信号Xv(a)的问题,可以利用压缩感知原理进行求解。 图3 OMP算法流程图 首先,定义M×N的观测矩阵Φ,Φ必须是与稀疏矩阵Ψ不相干的,随机高斯矩阵[12]和伯努利矩阵[8]都满足这一条件,另外M需满足式(5): K是自定义的稀疏度,本文选取随机高斯矩阵作为观测矩阵Φ,可以得到观测向量Y(a)=ΦS(a),已知Y(a),Ψ,Φ,K,输入到OMP算法程序中就可以求得Xv(a)的近似值Xv´(a)。之所以是近似值,因为X(a)中含有噪声项。但是由近似值Xv´(a)得到的时域信号Sv´(a),依然保留了原始振动信号Sv(a)的大部分特征,由式(4)可得: 其中,Ψγ是噪声的时域信号。在光纤其他位置由于不存在振动信号,所以信号S(z)=Ψγ是纯粹的噪声信号。由于噪声信号不具有稀疏性,所以如果我们执行同样的步骤会求得一个振动信号的伪值Sv´(z),显然Sv´(z)与S(z)之间并没有相似性。 这里定义重构误差: 其中,z表示光纤上的位置点。结合(6)、(7)式可知,振源处的重构误差δ(a)必然是小于1的数,利用这一点就可以定位振源位置。 本次实验的实验装置如图4所示,激光器线宽小于3 kHz,最大输出功率为10 mW,工作波长为1 550 nm。传感光纤的长度为2 km,探测脉冲频率1 kHz,脉冲宽度100 ns,压电陶瓷管(PZT)放置在1.6 km位置处。为验证上述理论,我们在PZT上施加50 Hz、200 Hz和450 Hz的混频信号,得到1 024条瑞利散射曲线,则我们在光纤链路的每一点上都得到一个包含1 024个数据点的离散信号S(z)。利用MATLAB软件生成2561024的随机高斯矩阵Φ,Ψ为离散傅里叶逆变换矩阵,设稀疏度K=10,带入OMP算法程序可得到沿光纤分布的重构误差曲线,如图5(a)所示, 图4 φ-OTDR系统实验装置图 图5 两种信号处理方法的结果对比 从图5(a)中可以看到,在1.6 km处的重构误差明显低于其他位置,据此就可以定位振源位置,图中虚线以下的部分是小于零的重构误差值,将1.6 km处的误差值与其他位置处小于零的误差值作比较,可得信噪比为12.2 dB,图5(b)是相同情况下分离平均法得到的定位曲线,经计算可得信噪比为2.1 dB,可见利用重构误差定位的方法具有更好的抗噪性能。 另外,OMP算法在确定振源位置之前,已经得到了光纤上每一点在频域的稀疏信号Xv´(z),但是单独取某一点的稀疏信号误差较大。为得到准确的振动频率,我们可以将所有重构误差小于0.8的稀疏信号Xv´(z)提取出来,相加求平均,这样求得的最大的频率分量就是我们要求的振动频率,如图6所示。 图6 振源处信号归一化频谱图 从图6中可以看出系统可探测的最大频率为500 Hz。基于压缩感知理论,由于我们在随机采样的过程中,相当于完成了对信号的压缩,即保留了信号的所有频域特征。所以其最大频率响应值可以达到采样定理的极限,即探测脉冲频率的1/2。本文中仿真系统的探测脉冲频率为1 kHz,则最大频率响应值为500 Hz。 本文首先简要介绍了φ-OTDR系统以及传统平均法定位的原理。在此基础上,针对传统的平均法在信号处理方面存在的问题,运用压缩感知理论提出了一种新的振源定位方法,采用OMP算法对光纤沿线各点的散射信号进行压缩与重构,通过求得的重构误差来进行定位。实验表明,对比传统的平均方法,本文提出的信号处理方法具有更大的频率响应范围,以及更好的抗噪性能。

3.2 基于压缩感知的φ-OTDR系统信号处理原理


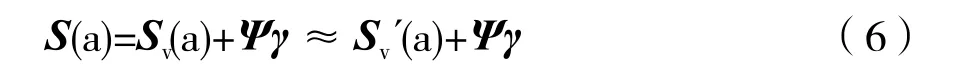

4 实验验证

5 结 语

