大学英语四级成绩预测建模与分析

【摘要】以本校16級学生为研究对象,在2017年12月首次参加四级考试的学生中随机选取100名样本,收集整理了他们大一两次期末成绩、平时成绩、高考成绩和CET-4考试成绩,利用软件Excel和SPSS,定量分析影响CET-4成绩的诸多因素之间的关系,建立多元线性方程模型,为今后CET-4成绩的预测、学校教学和学生管理提供参考。
【关键词】CET-4;相关性;多元回归方程
【作者简介】金灵,天津体育学院运动与文化艺术学院。
一、研究背景
大学英语四级考试(College English Test Band 4, 简称CET-4)始于1987年,是教育部高等教育司主持的全国性的教学考试。经历了三十多年的改革发展,四级考试已经成为反映学生英语水平和学校教学管理水平的一个重要指标,同时也是用人单位招募新人的一个重要参考,其重要性不言而喻。
众所周知,学习的结果与学前基础和学习过程有关。基于此,本文作者做出猜测,即大学英语四级成绩可能和学生高考英语成绩和大学英语课程成绩相关。那么,四级成绩是否与高考英语成绩、大学英语课程学业成绩有关?四级成绩与高考英语成绩、大学英语课程学业成绩之间能否建立出一个多元回归的数学模型?该模型又在多大程度上可以预测四级成绩?为了回答上述问题,本文借用社会科学统计软件包(Statistical Product and Service Solutions, 简称SPSS),将学生高考英语成绩与四级成绩、期末卷面成绩与四级成绩、平时成绩与四级成绩逐一做相关性分析,建立了四级成绩与高考成绩、平时成绩、期末卷面成绩之间的多元回归预测模型,并对回归模型的合理性和回归系数进行了检验,以期为学校英语教学和学生管理提供参考。
二、研究方法
1.研究对象。本文以2017年12月四级考试为依托,从中随机选取100名16级学生并对其入校前的高考英语成绩、大一两次平时成绩(简称平时成绩1、平时成绩2)、大一两次卷面成绩(简称期末1、期末2)和大学英语四级考试成绩进行收集和整理(数据来自教务处,截止到2018年12月)。利用Excel 和SPSS统计软件,对收集到的数据进行分析、研究和建模。
2.理论基础。多元回归分析是一种用于评价一个因变量和多个自变量之间关系的统计技术,其数学模型如下:
y= b1x1+b2x2+···+bnxn+c
该公式表示n个自变量共同作用于因变量y,其中bn是第n个自变量xn的回归系数,它代表的是xn 在多大程度上可以影响因变量y, c为常数项,为方程在y轴上的截距。用此方程,如果已知b1、b2···+bn,我们就可以预测y的值。
建立多元回归方程时应注意几点:1.线性关系。在回归分析中,因变量与自变量的关系应为线性关系,如果不满足这以前提的话,我们所得到的回归分析结果可能会过低地估计了变量之间的关系。因此在分析之前通过散点图等方式考查变量之间的关系是十分必要的。2. 多重共线性问题。多元回归方程要求各自变量之间有一定的互斥性。如果自变量之间高度相关,在回归过程中会彼此削弱各自对于因变量的影响,即多重共线性。多重共线性会使回归方程中得到的回归系数不稳定,所以需要SPSS进行多重共线性诊断。
三、研究结果
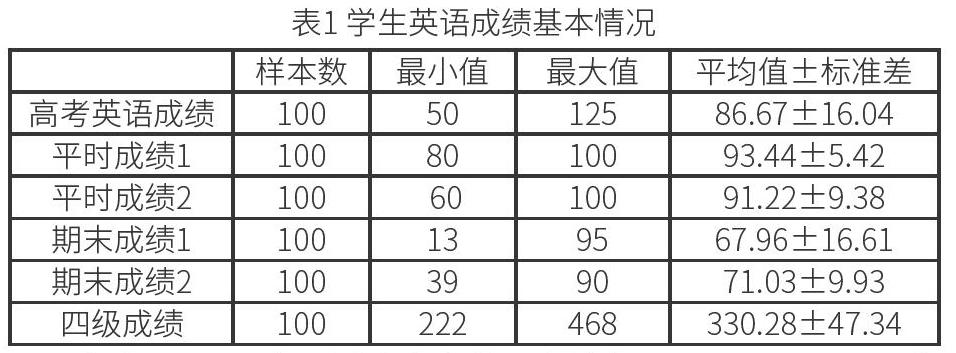
1.学生英语成绩的基本情况。通过描述性分析,得到学生英语成绩基本情况结果如表1所示:
由表1可以看出,样本高考英语成绩为86.67±16.04分。大一两次平时成绩分别为93.44±5.42分和91.22±9.38分,说明我校大一学生普遍出勤和课堂表现良好。大学第一次期末卷面成绩为67.96±16.61分,第二次期末卷面成绩为71.03±9.93分,表明我校学生在经过一年的学习后,英语水平有一定程度的上升。首次英语四级成绩为330.28±47.34。
2.学生英语成绩的相关性分析。在建立多元回归模型之前,首先要对自变量(平时成绩,期末卷面成绩,高考成绩)和因变量(四级成绩)进行相关性分析,绘制散点图。为了计算方便,本文将两次平时成绩和期末卷面成绩分别取均值,再进行分析。结果如下:
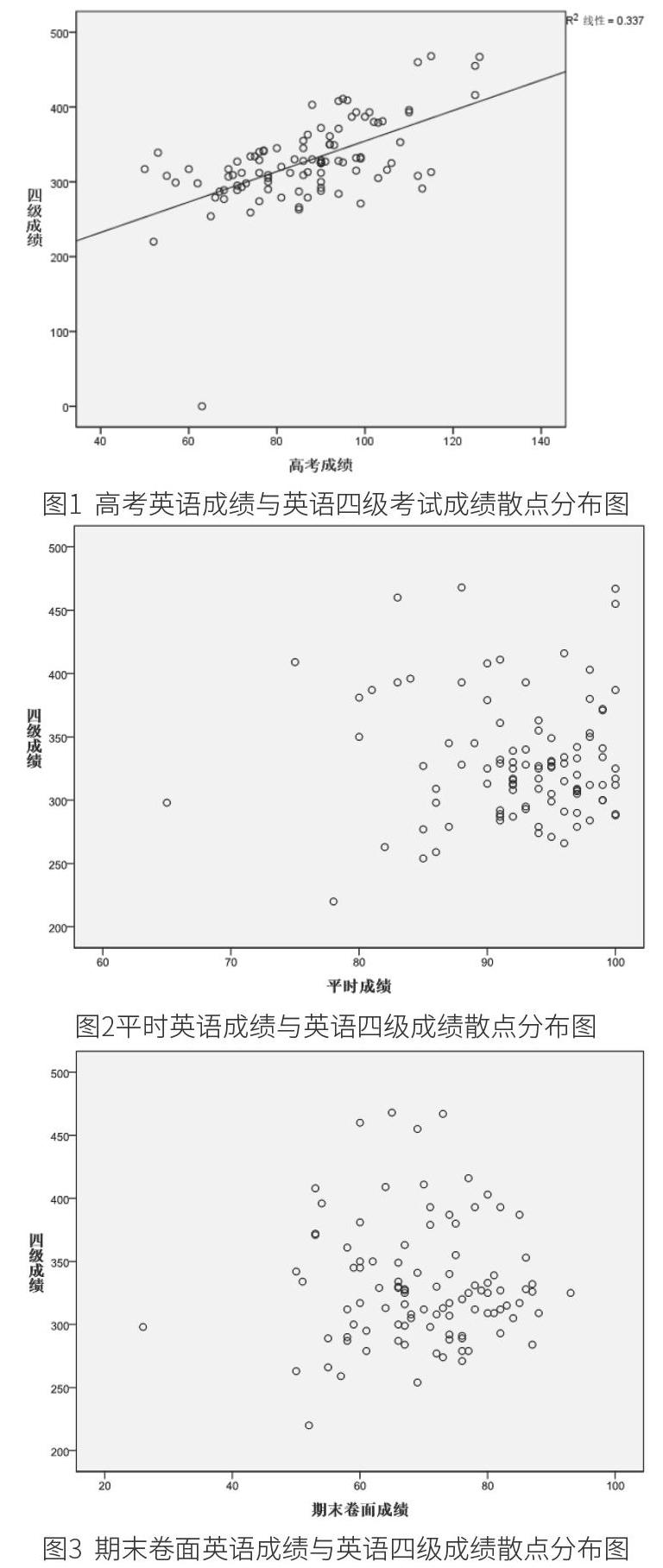
由图1看出,高考英语成绩与英语四级成绩基本呈线性关系,关系点也基本分布在线性关系曲线附近,由于存在其他因素的影响,有些关系点离线性关系曲线较远,但是基本呈线性关系,说明高考英语成绩可以作为影响英语四级成绩的一个因素。
由图2看出,数据点大多集中在90~100分数段之间,大一平时成绩与英语四级平时成绩并不呈现出线性关系,说明平时成绩对四级考试的影响并不大,可以剔除其作为因变量进入方程模型。
由图3看出,相比平时成绩,期末卷面成绩的数据点分布相对规律,但也无法呈现线性关系,说明期末卷面成绩和四级成绩相关性很弱,可以不将其纳入回归方程。
综上所述,只有高考英语成绩和四级考试成绩呈现出良好的线性关系,可以作为自变量进入方程。
3.模型建立。利用SPSS软件对收集到的数据进行回归分析处理,得到处理后的数据。
表2体现的是拟合优度检验,说明自变量和因变量形成的散点与回归曲线的接近程度。从表中可以看出,模型拟合度为61.8%,说明回归过程所选用的预测变量(高考英语成绩)在很大程度上能够解释相应因变量(四级英语成绩),因此可以用该模型来预测四级考试成绩。
表3为单因素方差分析表,表明高考英语成绩对四级英语成绩有显著的效应, F0.05(1,98)= 60.650,P<0.05。从表4系数表中我们清楚地得出高考英语成绩和四级英语成绩的相关系数为1.784,影响概率P值趋于0。因此,可以再次证明高考英语成绩和四级英语成绩的线性相关程度很高。
通过分析得出预测英语四级成绩方程:

