机场跑道航空器拦阻系统动力学分析

尹 涛，冉振华，王有杰

（天津航天瑞莱科技有限公司北京分公司，北京 100076）

由机械事故、恶劣天气、跑道异常、驾驶员失误等导致飞机冲出跑道是最典型的航空飞行事故形式之一。跑道拦阻系统（EMAS, engineered materials arresting system）可在飞机冲出跑道的情况下有效地阻滞飞机，对确保飞机关键构件和机上乘客的安全有重要作用[1]，近年来对其动力学行为[2-4]及阻滞材料特性[5-6]的研究成为航空地面设备领域的热点。

王维等[2]关注阻滞距离、阻滞历程加速度的变化情况，以考察EMAS 对整机的作用是否达到预期目的。朱剑毅等[3]、李波等[4]研究了阻滞过程中的载荷是否足以破坏飞机机体结构。然而，无论是关注宏观阻滞过程抑或飞机局部构造的强度，都需要对EMAS 系统进行准确建模，其关键在于处理阻滞材料对飞机的作用力。为此，文献[3-4]对阻滞材料的特性进行了研究，并建立阻滞力模型及其数学表达式，文献[2]应用伯努利方程的经验公式来计算阻滞系数。现有文献多采用经验公式处理该问题，可用于揭示EMAS 的一般动力学规律，但是在具体分析由某种特定阻滞材料构成的EMAS 时会带来较大误差。

综上所述，采用实验数据拟合的方式得到材料阻滞系数，并将该系数引入EMAS 动力学方程，可以较准确地预测飞行器在阻滞过程中的加速度、速度等参数的时间历程，为后续起落架强度和阻滞区的尺寸设计提供参考。

1 EMAS 动力学模型

1.1 符号及其意义

相关几何、力学参数及其意义如图1 和表1 所示。

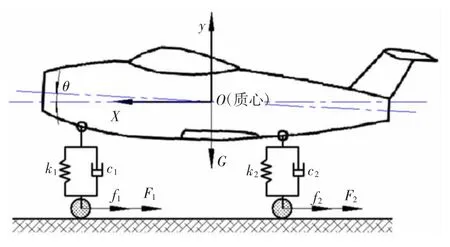
图1 飞机动力学模型Fig.1 Airplane dynamic model

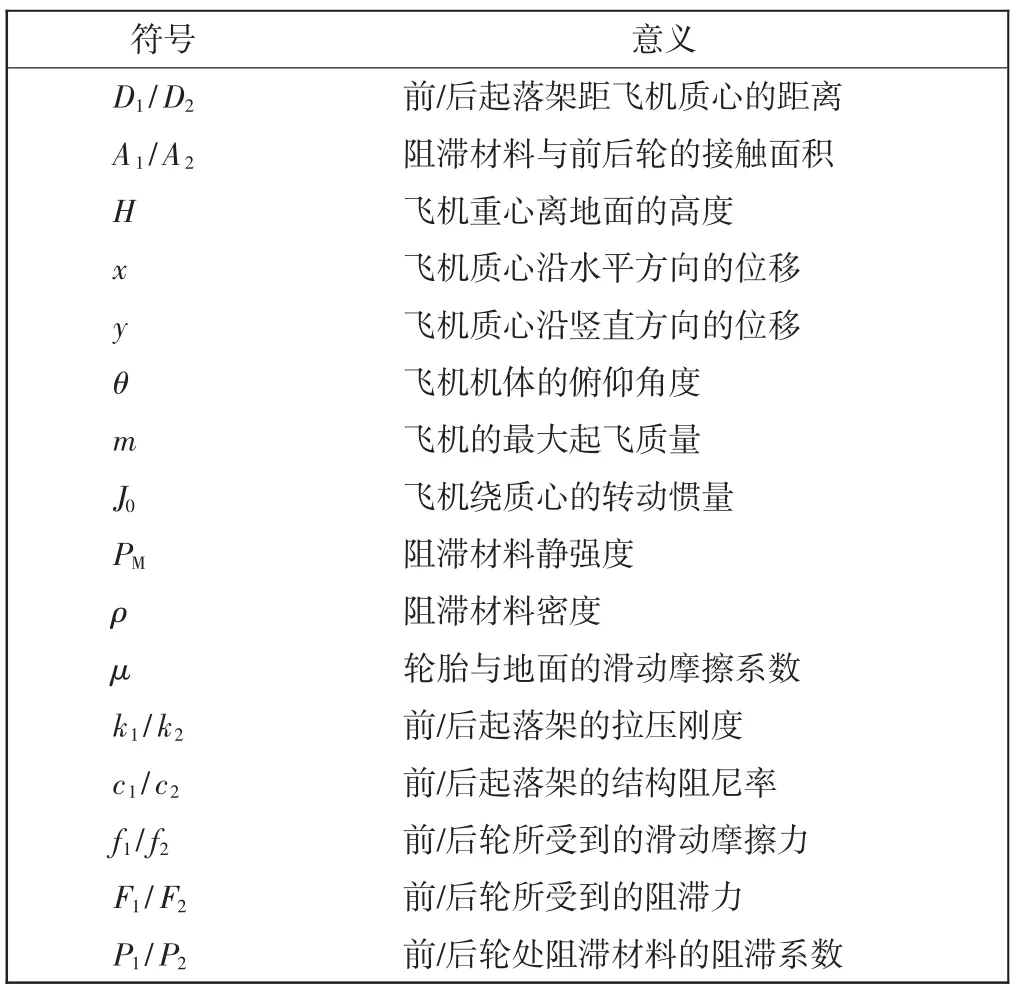
表1 参数及其意义Tab.1 List of parameters

1.2 EMAS 动力学方程

将飞机机体处理为刚体，两个方向的平动和俯仰作为系统自由度；将前后起落架等效为弹簧-阻尼元件。使用拉格朗日方程对图1 所示模型进行描述，即

其中：qj为广义速度；Qj为对应于qj的广义力。系统动能为

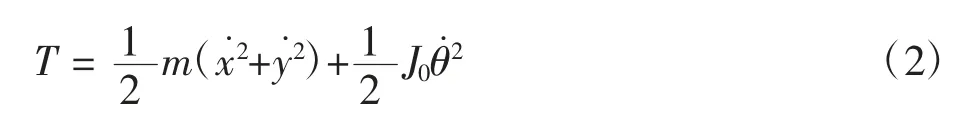
系统势能（将弹性势能0 点设置为静平衡点）为

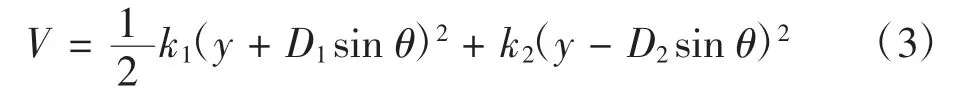
耗散函数为

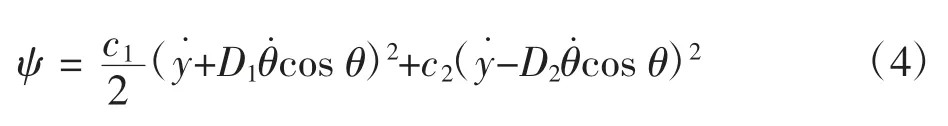
非保守广义力为

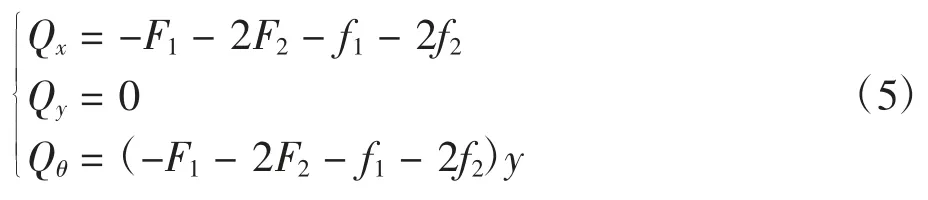
将式（2）～（5）代入式（1），并将飞机俯仰角度处理为最小量，可得

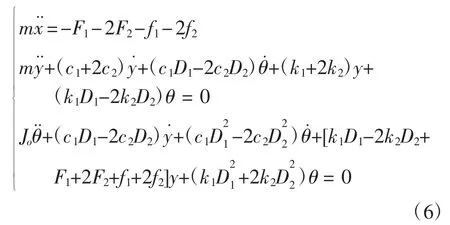
式（6）中摩擦力的表达式为

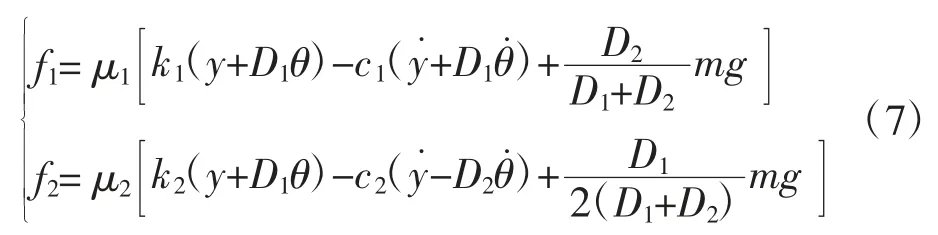
式（6）中阻滞力可由阻滞率和接触面积在竖直方向上的投影面积得到，即

至此，式（6）所示的常微分方程组即为EMAS 系统动力学方程，注意到：

1）x 自由度与其他两自由度的耦合并不大。其他两自由度的运动方程中并未出现与x 方向的位移及其导数相关的项；而在x 方向，由于阻滞力和重力引起的摩擦力在激励力中占主导地位，使得其他两自由度通过影响正压力从而影响摩擦力所产生的效果很小，这一点可从原模型的求解结果得到验证。

2）θ 自由度和y 自由度相互耦合，但其激励力为0，在零初始条件下，其解很小，甚至为0，则式（7）可简化为

后轮通过的阻滞区与前轮相同，只是滞后一定的距离，即

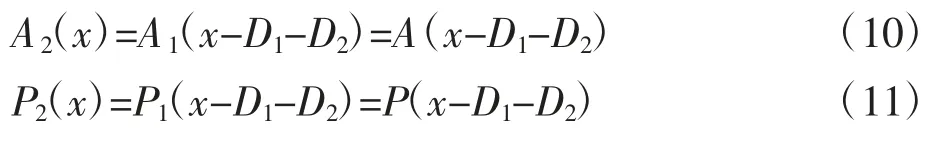
其中：P 为阻滞系数。则式（6）可最终简化为

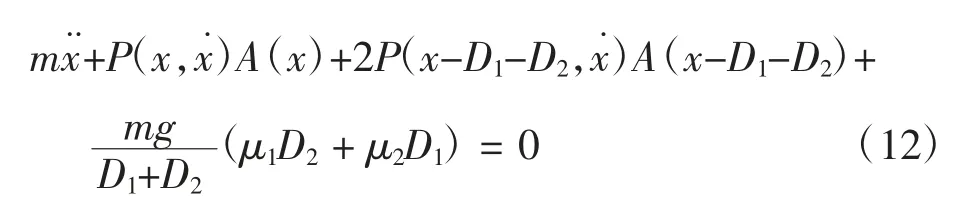
综上，式（12）成为考察EMAS 水平方向运动情况的非线性常微分方程，在给定初始速度的情况下，可采用数值计算方法求解初值，获得阻滞过程中位移、速度、加速度的变化情况。计算式（12），还需确定：

1）阻滞区与飞机起落架竖直接触投影面积A（x）在水平方向上的变化关系可表示为轮宽W 与阻滞区厚度HA（x）的乘积，即

2）描述阻滞系数随水平方向坐标（由多种阻滞材料混合铺设而成）与阻滞速度变化（阻滞材料本身的特性）关系的P（x），其量纲与压强一致，表征单位体积的阻滞材料被破坏时所吸收的能量，可采用经验公式，算例仿真部分将详细讨论由实验数据拟合获得该系数的方法。

2 阻滞系数

2.1 阻滞系数经验公式

对于阻滞材料的阻滞系数，常见的经验公式有常阻滞系数模型和与速度呈二次关系的阻滞系数模型。常阻滞系数模型假设其阻滞系Pc数与当前阻滞速度无关、仅与阻滞区厚度相关，即

另一类经验公式形同流体力学中的伯努利方程，认为其阻滞系数Pe与速度的二次方有关，即

所建模型中，阻滞系数可理解为材料动强度，与材料静强度、材料密度、阻滞速度有关。由于阻滞材料种类和成分多样，某些材料采用上述经验公式可能存在较大误差。在实验数据充足的情况下，为了更好地描述特定阻滞材料的特性，可完全基于实验数据拟合实现确定形式的阻滞系数表达式，取线性关系为

其中：Pl为试验数据拟合的阻滞系数；C0为阻尼系数；K0为弹性系数。

2.2 实验数据的引入

上述3 种组织系数模型都需要相应的实验数据支撑，因此，对某型泡沫阻滞材料进行试验。使用INSTRON高应变率液压伺服试验机，该设备可控制试验机的活塞以设定匀速运动，使加载到试验件的位移速度恒定，如图2 所示。试件在变形过程中可基本保持恒定应变率，而试件所受应力、应变由试验机系统测量的载荷和位移通过计算得到。

图2 实验装置示意图Fig.2 Illustration of experimental set

材料在一定压缩速度下的典型位移-应力特性曲线如图3 所示。

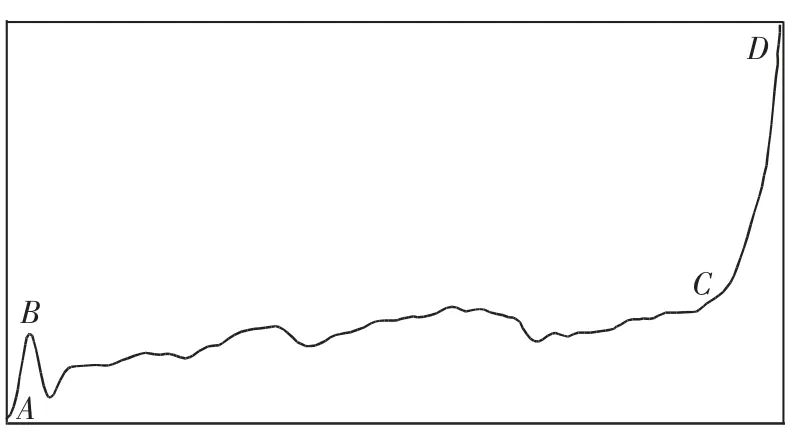
图3 典型的阻滞材料实验曲线Fig.3 Typical experimental results of arresting materials

典型的试验曲线反映了泡沫材料的3 个变形阶段，即：弹性区（A～B）、屈服平台区（B～C）和致密区（C～D）。不同规格试验件的试验曲线在各阶段的斜率和各点的数值略有不同。

由阻滞系数的物理意义可知，对每个压缩速度下试验曲线的A～C 段进行积分，可得试验压缩速度下的阻滞系数为

其中：sC为C 点应力；τ 为位移。

测试多个压缩速度下的阻滞系数，并利用式（16）进行线性回归，可得阻滞系数随速度变化的具体表达式，对试验材料的拟合结果为

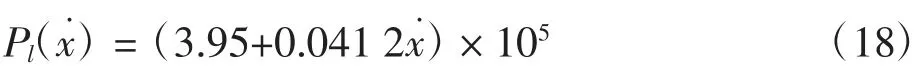
同时，可通过准静态下的压缩实验获得材料静强度，与材料密度一起代入式（15），得到试验材料阻滞系数的经验表达式，即

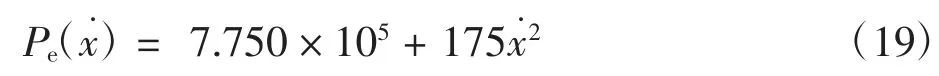
式（18）～式（19）计算所得阻滞系数与实验数据的对比如表2 所示。

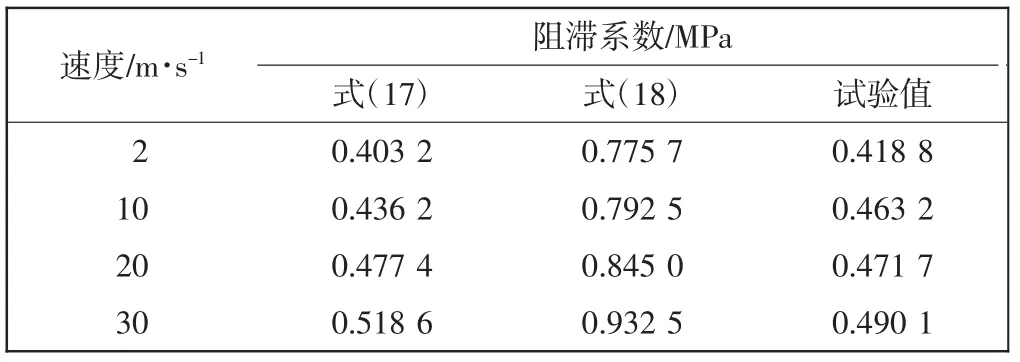
表2 阻滞系数的计算及试验结果Tab.2 Calculated and tested arresting ratioes

由表2 可知，式（14）所需实验数据虽然较少，但其所得阻滞系数误差较大。而直接由实验数据拟合得到的阻滞系数表达式虽在不同材料间不具备通用性，却可以较好地描述当前材料的阻滞系数与阻滞速度之间的关系。因此，后续将采用式（16）和式（18）所得阻滞系数以适应所选材料、减小误差。

3 B737-700 阻滞过程

根据B737-700 飞机的相关参数，利用式（16）分析其在如图4 所示的等厚度阻滞区铺设情形下的阻滞过程。其中，B737-700 前后起落架距离取12.58 m，进入引导区的初速度为36 m/s，EMAS 引导区长20 m，阻滞材料高0.4 m。

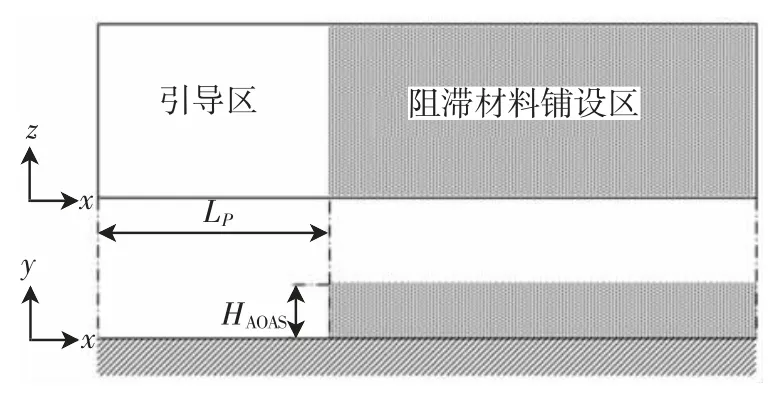
图4 阻滞区的等厚度铺设示意图Fig.4 Arresting zone layout illustration with uniform thickness

采用龙格库塔法计算EMAS 动力学方程，得到阻滞过程中位移、速度、加速度的变化过程，如图5 所示。

为说明上述结果的合理性，可将其表述为“加速度-位移”关系和“速度-位移”关系，如图5（d）～5（e）所示。以图5（d）为例，加速度突变点标记为A～E，造成各阶段加速度变化及突变的原因为：A 点之前，飞机前后轮均未进入阻滞区，仅受地面摩擦力作用，产生恒定的加速度；AB 段，飞机前轮进入阻滞区，突然受到阻滞力；BC 段，飞机的前起落架位于阻滞区，同时受地面摩擦力及阻滞力，后起落架位于引导区，只受地面摩擦力，阻滞力随速度的减小而减小，因此加速度绝对值逐渐减小；CD 段，后轮进入阻滞区，突然受到阻滞力，由于后轮面积比前轮大，因此带来的影响要大于AB 段；DE 段，飞机前后轮均进入阻滞区，阻滞力随速度的减小而减小，因此加速度绝对值逐渐减小。E点之后，速度为0，加速度突变为0。

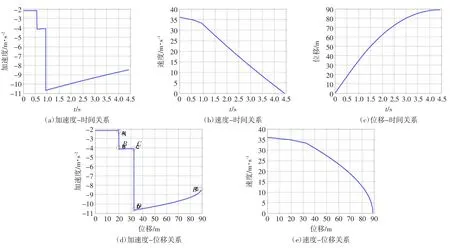
图5 阻滞过程各参数关系Fig.5 Parameter relation during arresting process

4 参数取值对阻滞过程的影响

利用EMAS 系统研究飞机阻滞过程主要考虑以下两类参数：①飞机相关参数，如飞机的初速度、质量、前后起落架的面积等；②阻滞区相关参数，如阻滞区铺设方式、引导区长度、阻滞材料性能等。

选取一组参数进行阻滞过程分析时，阻滞距离和最大加速度较为重要。阻滞距离是指飞机最终停下时侵入阻滞区的距离，是阻滞区长度设计的主要参考指标。最大加速度是指阻滞过程中的最大加速度幅值，决定阻滞过程中的人员安全，也是飞机关键设备（如起落架等）强度安全设计的重要参数。

基于试验阻滞材料性能参数和B737-700 飞机相关参数，按照如图1 所示的等厚度阻滞区铺设方式，计算不同阻滞区厚度下飞机初速度对阻滞距离和阻滞过程最大加速度的影响，如图6 所示。

由图6 可以看出：

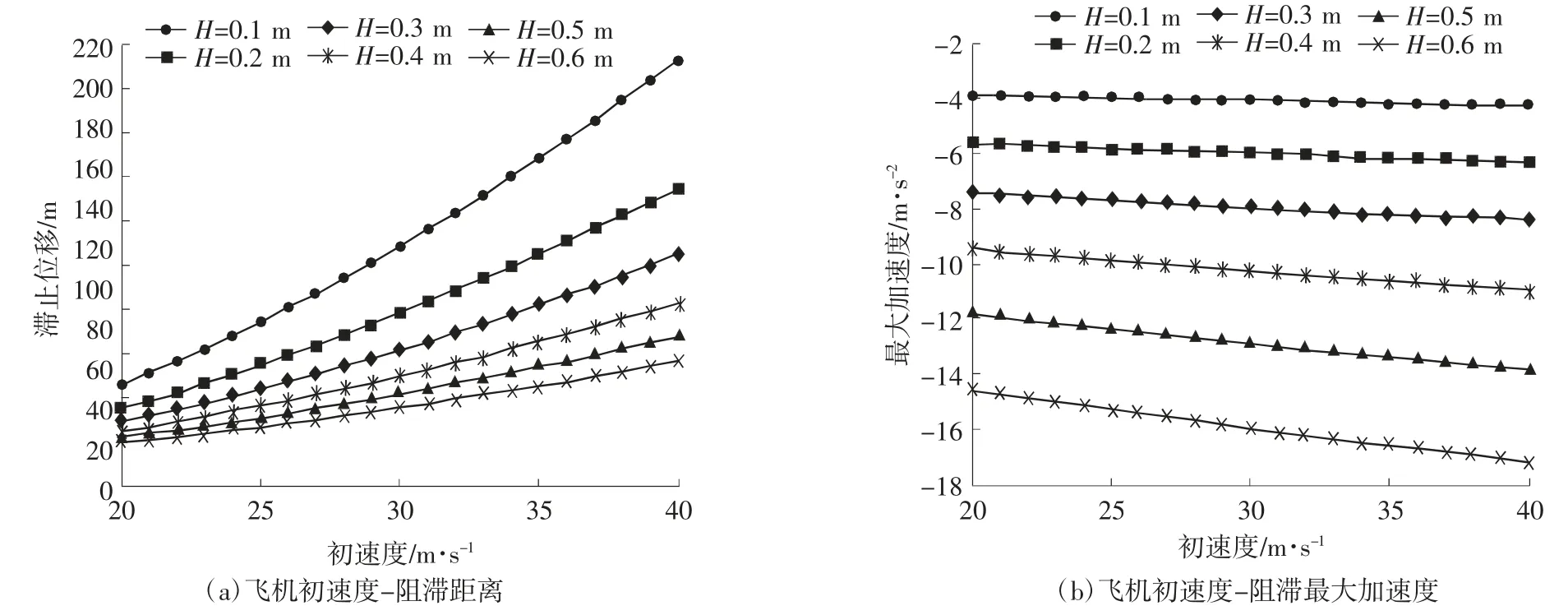
图6 不同阻滞区厚度下飞机初速度与阻滞的关系Fig.6 Initial velocity vs.arresting parameters under different thickness of arresting material

1）相同初速度下，阻滞区厚度越大，阻滞距离越短，阻滞过程的最大加速度越大。随着阻滞区厚度的增大，其对阻滞距离的影响逐步减小，对阻滞过程最大加速度的影响逐步增大。

2）相同阻滞区铺设高度下，飞机的初速度对阻滞距离和阻滞过程的影响呈线性关系。

5 结语

建立了EMAS 动力学模型，在该模型中，区别于传统的常阻滞系数模型及经验模型，提出一种基于实验数据拟合的阻滞系数计算方法。以某型泡沫阻滞材料为样本进行实验，给出了实验数据的处理方法，并将该方法与经验公式所得结果进行比较。结果表明，经验公式所得阻滞系数在样本阻滞材料中误差较大，而直接由实验数据拟合得到的表达式却可以较好地描述当前材料的阻滞系数与阻滞速度之间的关系。

基于上述模型及方法，利用B737-700 飞机参数计算了阻滞过程各参数并说明了结果的合理性，最后给出阻滞区高度、飞机初速度对阻滞距离和阻滞过程最大加速度的影响。结果表明，虽然增大阻滞区的厚度有助于在较短距离内阻滞飞机，却会引起阻滞过程最大加速度的迅速增大，因此，在考虑飞机以较大的初速度进入阻滞区时，应合理设计阻滞区的厚度变化规律。