精度试验数据统计方法研究*

张志辉

（91404部队 秦皇岛 066001）

1 引言

在对探测类设备的测量精度进行试验验收时，由于陪试目标的速度越来越快，获得的数据样本量越来越小，特别是光学探测设备，由于作用距离较近，一次进入获得样本极少［1～6]。因此我们需要在少量试验样本条件下，研究对测量精度试验数据的科学统计方法。

2 常用统计方法

对测量精度的统计方法常用有两种，一种为采用样本2阶中心距对方差σ2进行估计［7～9]：

该方法是利用已获试验样本数据的方差估计总体样本方差，方法直观，易于理解，较为常用。但该估计量的期望为

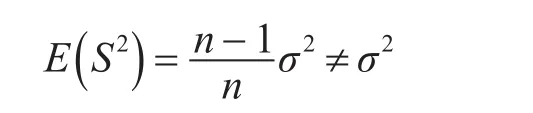
即用2阶中心距S2对方差σ2估计不满足无偏估计要求。

为使估计量的期望为σ2，从2阶中心距S2演变出另一种对方差σ2估计量［7，10～11]为

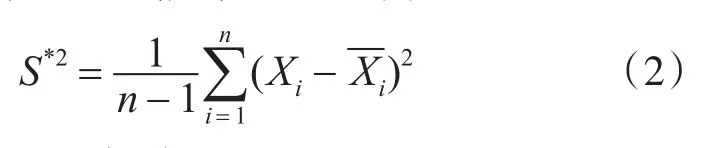
3 从风险角度分析2种统计方法优劣

假设探测设备的精度指标要求为1，探测设备按照精度1进行设计。假设探测设备验收试验测量值为X，X满足标准正太分布：

可知［7，12]：

使用2阶中心距S2对方差σ2进行估计时，研制方风险为α1，使用方风险为β1，则：

图1 用2阶中心距S2估计方差σ2时研制方和使用方风险

从图1可以看出，当试验点数较小时，研制方风险很小，使用方风险较大。即对一个测量设备验收试验时，采用1000以下样本数对的测量精度进行评价，对使用方不利，对研制方有利。图中由于纵轴间隔不等，造成风险曲线有拐点。

使用无偏估计S*2对方差σ2进行估计时，研制方风险为α2，使用方风险为β2，则：

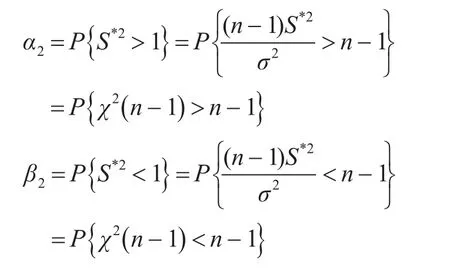
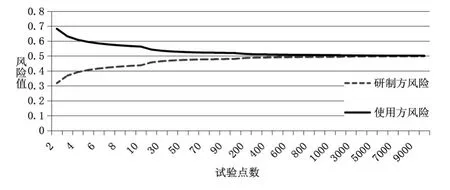
图2 用无偏S*2估计方差σ2的研制方使用方风险

同样可以从图2看出，当试验点数较小时，研制方风险很小，使用方风险较大。即对一个测量设备验收试验时，采用100以下样本数对的测量精度进行评价，对使用方不利，对研制方有利。

对比图1和图2可以看出，相同试验点数情况下，无偏估计方差σ2的研制方和使用方风险差距更小，即试验点数小于1000时，用S*2对方差σ2估计更优，试验点数大于1000时，两种统计方法相当。因此，用S*2对方差σ2估计更优。

4 改进统计方法

既然用S*2对方差σ2估计更优，我们不禁要问，该统计方法是否为最优？最否有更优的统计方法？

我们同样从风险角度出发，最优统计方法应当是研制方和使用方风险均为0.5时。

参照S2到S*2演变的过程，最优统计方法应当为如式（3）：

则：

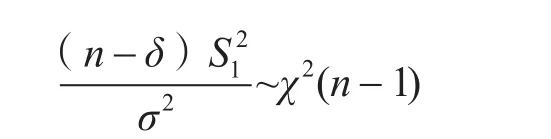
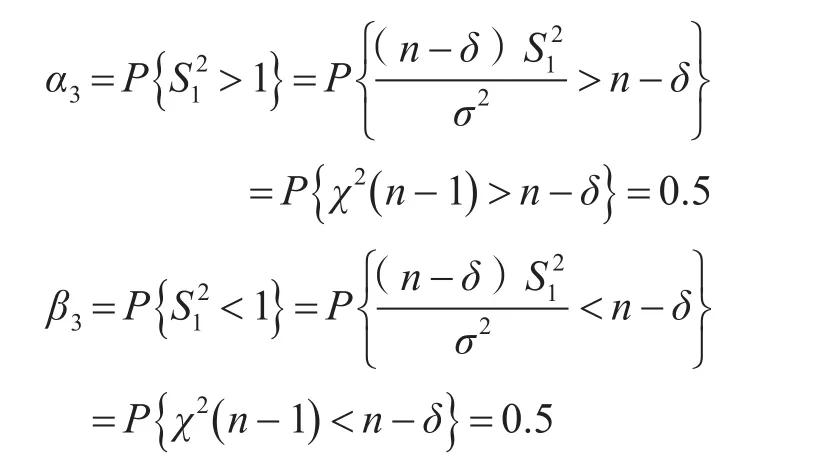
可得：

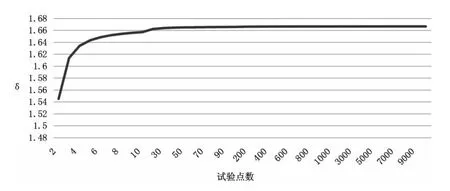
图3 δ随试验点数n变化情况

为了简化计算，可取δ=5/3，得：

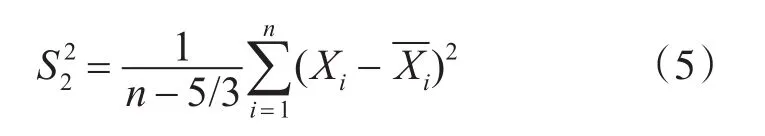
图4 用估计方差σ2的研制方使用方风险

从图4可以看出，除试验点数n=2时外，其余试验点数时研制方和使用方风险接近0.5，满足双方风险相当原则。研制方风险约大于使用方，且差距较小，满足探测设备的精度指标验收试验要求。因此用对方差σ2进行估计优于S*2，当试验点数n大于2时，均可使用；当试验点数n=2时，可选用对方差σ2进行估计。

5 仿真验证

采用Matlab软件工具，通过仿真试验的方式，验证三类统计方法优劣。每次试验取试验点数n=10，试验10000次。每次试验分别采用三类统计方法对方差σ2进行估计。其中每次试验的各点测量结果用Matlab软件工具randn函数生成均值为0，方差为1的正太伪随机数。统计结果如表10。

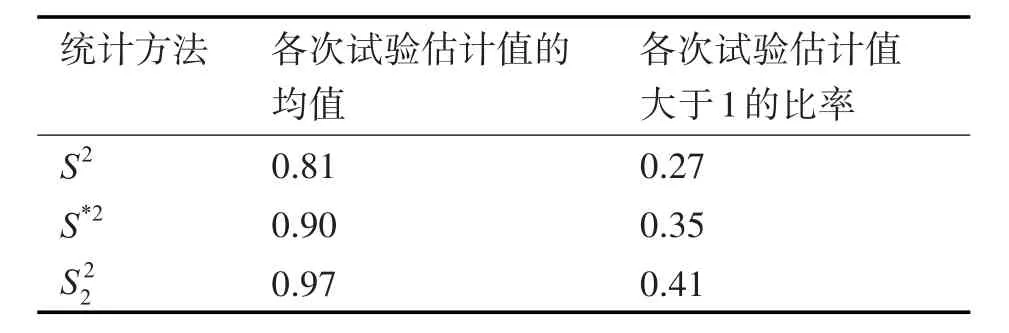
表1 三类统计方法试验结果比较

6 结语

从试验风险角度出发，分析了现有2阶中心距S2和无偏估计S*2两种常用的统计方法，推导计算了两种统计方法的研制方和使用方风险，比较了两者之间的优缺点，确定了两者的适用范围。同时根据试验双方的风险相当原则，参照S2到S*2演变的过程，在无偏估计S*2基础上，改进统计方法，适用于少量样本时对方差σ2估计。