基于加速度的笛卡尔坐标系目标运动点迹模拟

崔威威，姚 远，曹德建，刘 硕，鲍鹏飞

(中国船舶重工集团公司第七二四研究所，南京 211153)

0 引 言

雷达数据处理算法仿真、验证面临若干问题，包括采集数据成本高、目标运动模型少、极端运动目标难复现、目标活动空间有限、非合作目标缺少真值等。这些困难导致目标典型运动处理样本少，数据处理与数据融合算法适应性测试、训练和分析空间有限，不能满足复杂运动数据处理、多平台数据融合需求，难以实现处理算法的深入分析和持续改进。目前，点迹仿真领域论文较少，存在运动模型简单的情况。本文为统一描述目标运动、简化模型，忽略重力、阻力影响和地球曲率影响，简单假设目标仅仅在法向、切向存在加速度值，研究了二维空间不同加速度情况下的目标运动、目标投影变换、雷达扫描判断计算公式。分析表明，本文讨论的方法可以输出高精度的目标运动轨迹。

1 仿真模型

1.1 目标运动方程

雷达目标由速度方向、法向加速度方向决定作二维空间运动，为此根据加速度情况将目标运动划分为匀速直线、匀加速、圆周、自由运动等4类。

1.1.1 匀速直线运动

目标在[0,t]时间内没有切向、法向加速度的情况下，即目标保持匀速直线运动，假设目标初始位置是(x0,y0)，目标的初始航向是w0，此时目标的位置按照下式计算：

x=x0+vtcos(w0)，y=y0+vtsin(w0)

1.1.2 匀加速直线运动

目标仅在[0,t]时间内切向上存在加速度，即目标保持匀加速直线运动，此时目标的位置按照下式计算：

1.1.3 匀速圆周运动

目标在[0,t]时间内仅存在法向加速度，即目标保持匀速圆周运动，此时目标的位置按照下式进行计算：

其中，w=a/v，r=v2/a。

1.1.4 目标自由运动

在[0,t]时间内同时存在法向加速度an>0和切向加速度at>0，那么首先根据获得目标航向变化率：

其中，w0表示初始航向，航向变化按照下式计算：

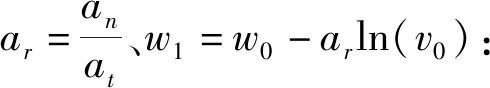
w(t)=arln(v0+att)+w1

考虑速度x、y方向的速度(以y轴为正北)：

以x方向速度作为分析对象。考虑到速度积分公式：

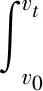
因此得到

同样得到Sy(t)：

为保证飞机等空中目标在完成一系列机动后保持在固定高度运动，提供一个标记位指示目标在规定的时间内完成改平动作。为此假定目标在1 s完成这个修正过程，从而根据目标的姿态和速度计算得到一个附加的加法向加速度描述向量。

1.2 空间变换

假设目标在三维坐标系内仅受法向和切向加速度影响，那么目标在由切向加速度和法向加速度决定的二维平面上运动，其运动过程由1.1.2～1.1.4描述；为解决三维空间内目标运动位置计算，需要解决投影变换问题。在按照公式计算目标位置后，将目标在特定二维空间的轨迹投影到三维空间，完成目标实际位置更新。

为此，定义切向加速度(at,θ,φ)、法向加速度值(an,λ)，其中at∈R、an≥0分别是切向和法向的加速度值；航向角定义为(θ,φ)，θ是和航向与x-y平面的夹角，φ是航向角在xy平面上与x正轴的夹角，在法向加速度为0时，认为目标在经过旋转一定角度后的当前相对位置所在的x-y平面上运动，要求旋转后的平面与原x-y平面形成等于航向夹角θ。由于认为目标在由速度方向、法向加速度方向决定二维空间作运动，因此简单定义法向加速度的方向λ为x-y平面逆时针旋转的角度。

推导三维投影到二维的变换矩阵：

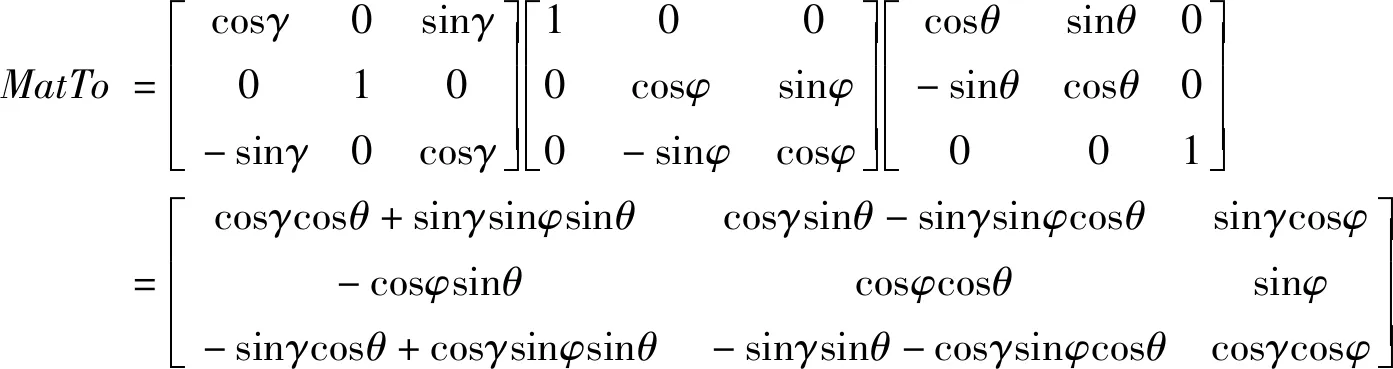
同时得到二维～三维的变换矩阵：

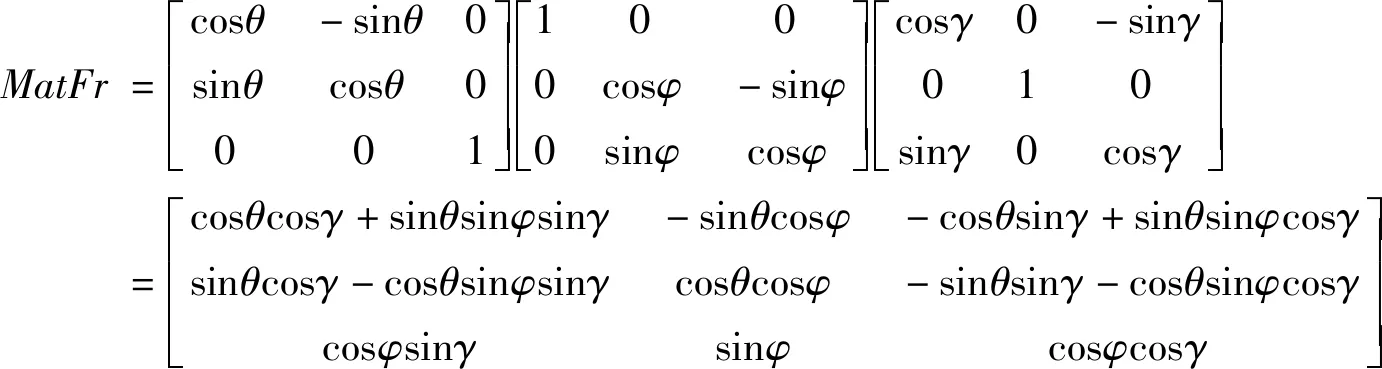
1.3 雷达扫描公式

假设[t1,t2]时间内雷达的法线方向是[θ1,θ2]，目标相对于雷达所在平台的方位角是[φ1,φ2]，经过过零点处理，如果不存在φ2<θ1或者θ2<φ1，那么认为目标被扫描过，经过适当的迭代次数可以获得目标被扫描过的时间。

假设雷达的工作模式为扇扫和环扫，那么环扫目标的方位计算为

w=mod(w0+ω(t-t0),360)

其中，w0是雷达初始法向方位；t0是雷达延迟开机时间；ω=2π/T是天线扫描角速度，T是天线周期。

扇扫雷达的法向首先对雷达初始方位w0、最左侧扫描角度wl和最右侧扫描角度wr的扫描范围做过零点处理，确保wr>w0>wl，并假设t0是开机时间，并定义一个扫描周期为T，那么

如果目标在计算步长内相对平台的起始结束角度为[θ1,θ2]，雷达法线为[θ1,θ2]，如果存在[θ1,θ2]与[θ′1,θ′2]交叉情况，那么认为目标被雷达探测。在目标被雷达探测到时，通过迭代获得目标在被扫描到时刻的精确位置。

1.4 采样计算与迭代次数

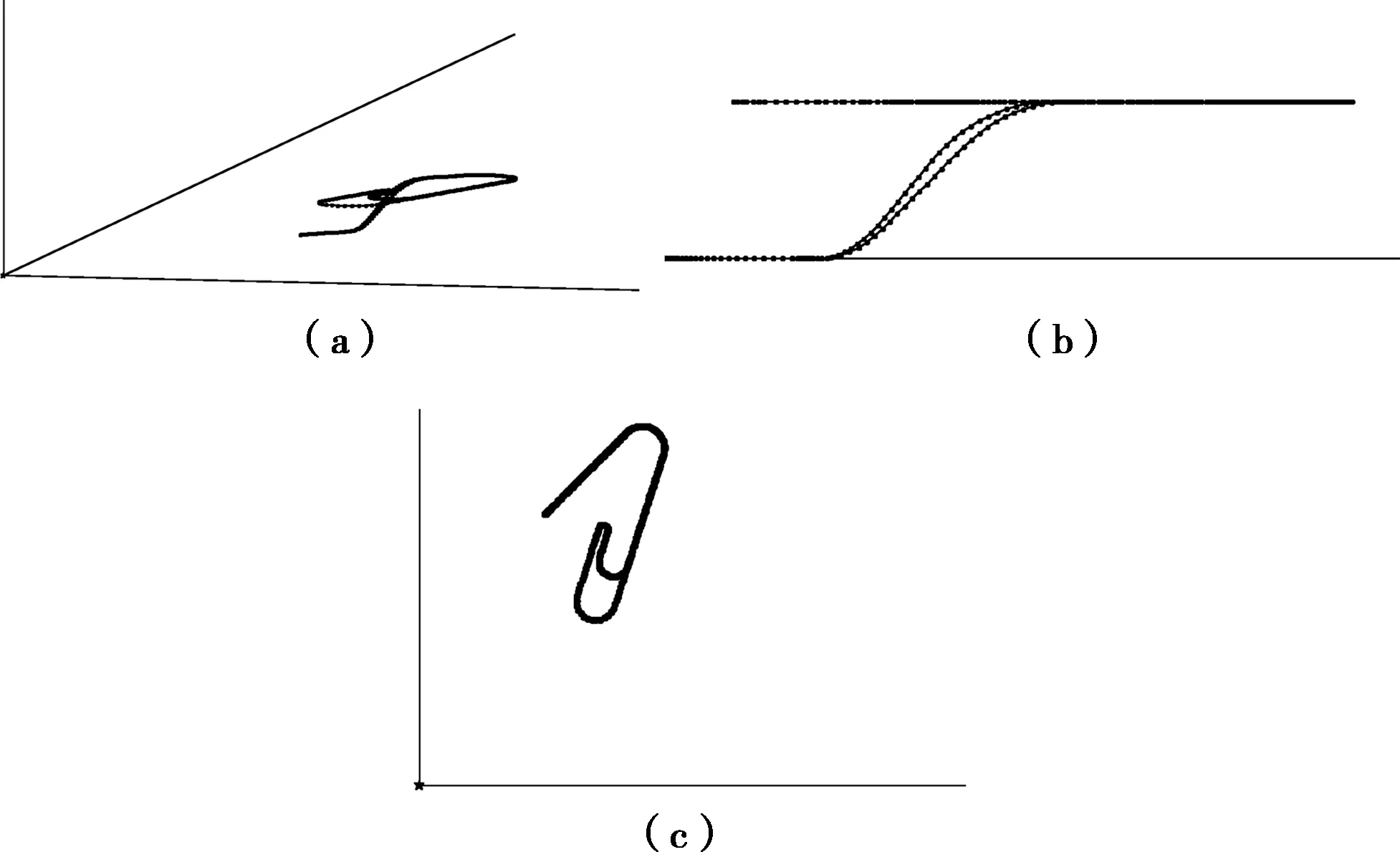
每个计算步长动态划分为若干采样时间段，确保在每个相邻的采样时间段[t1,t2]内目标被1个雷达仅扫描到1次。因此，计算步长不得超过扇扫雷达或者环扫的最短扫描周期，确保计算步长内不丢失目标点迹。如果存在扇扫雷达在[ts,te]计算步长内的t′m时刻完成扫描方向转换，存在环扫雷达在t′n扫过0点，排序后的时间{t′i}满足ts

如果判断[t1,t2]时间内目标被扫描过，默认均匀分割时间进行采样计算，迭代计算8次得到输出的目标位置。如果每个步长设为1 s，均匀划分10次，迭代8次意味着时间精度达到εt=O(10-8)，位置数值误差εd=O(v(10-8))(v是目标的运动速度值)。因此，本文提出的方法可输出高精度的目标位置，同时没有增加太多计算量。

1.5 数据处理流程

首先给出目标运动初始状态和加速度过程定义，目标分为普通目标和雷达平台目标。目标初始状态包括目标在三维空间的位置、轴向速度、运动方向基本信息；加速度过程分为轴向加速度过程和法向加速度过程两类，每个加速度过程状态包括加速度类型标识、开始时间、运动结束时间、加速度值，法向加速度还需要一个角度参数来描述运动平面与x-y平面的夹角。通过运动初始状态和加速度向量定义，得到了目标运动的全过程描述。

其次给出雷达扫描参数，包括雷达工作模式、开机时间、初始法向方向、扫描周期、探测距离、探测仰角范围、方位误差、仰角误差、距离误差、平台时间误差、方位精度、仰角精度、距离精度，其中工作模式简单分为环扫和扇扫。每个雷达和1个雷达平台目标关联，但1个雷达平台目标可以搭载多个雷达。

在完成初始状态设定后，按照给定的计算步长进行计算。利用相关公式分别获得计算步长内的目标位置信息、天线法向方位信息，进而计算目标的相对雷达的方位角度、仰角、距离信息。根据雷达的仰角范围、距离范围、探测方位范围进行扫过判断。如果判定扫过且目标相对距离在探测范围内，则进行迭代计算，直到获得指定精度的目标位置；如果判定有点迹输出，并基于误差信息修正目标的相对位置(仰角、方位角和距离)和时间作为输出的点迹，在完成全部目标的扫过判断后对输出点迹按照时间进行排序。如果需要输出带有随机误差的结果，利用方位精度、仰角精度和距离精度参数产生随机数修正输出点迹的方位、仰角和距离。

2 实验验证

随意设置目标与平台的位置为(12 578 6 421 1 000)、(5 480 3 158 0)。二者皆以10 m/s、60°作为运动初始状态，并都在0～600 s受到10 m/s2的加速度，雷达周期设为3 s。那么可以预测，所有输出的点迹的方位、距离、仰角都是一致的，前后两个点的时间间隔为扫描周期3 s。图1为目标的点迹。

图1 运动但相对保持静止的平台与目标输出结果

可以看出，三维图中仅仅出现一个点迹，经检查输出点迹结果，600 s内共输出187个点迹，前后两个点迹的时间差皆为3 s，输出点迹的时间、方位角、仰角、距离分别是(0.544262+3k，65.311429，7.294574，7 875.834 749)，k=1,2,…,n。这说明了本方法可提供高精度的输出结果。

模拟了一个固定雷达监视飞机起飞、降落的过程，得到飞机的轨迹见图2。图2(a)为全局图，图2(b)为X-Z视图，图 2(c)为X-Y视图，其中雷达的周期是1.5 s。

飞机的切向加速度见表1，飞机的法向加速度见表2。可以看出，研究成果可以提供目标复杂运动过程仿真。

图2 目标运动轨迹

表1 飞机的切向加速度值

表2 飞机的法向加速度值

3 结束语

本方法能够实现三维坐标系目标自由运动与雷达扫描仿真，提供高精度的目标真值点迹，满足雷达数据处理需求，具有较高的工程实践价值。目前，本方法并未考虑地球曲率、地球引力、流体阻力等因素对目标轨迹的影响，这是后续工作需要解决的难题。