基于等效电路模型的基片集成波导滤波器快速设计方法

马 亮，倪大海，李 江，邝小乐

(1.中国船舶重工集团公司第七二四研究所，南京 211153；2.中国船舶重工集团公司第七二三研究所，江苏 扬州 225101)

0 引 言

基片集成波导(SIW)滤波器是近年来备受关注的一项技术。它类似于传统矩形波导滤波器，具有低损耗、高Q值等优点。同时，基片集成波导滤波器尺寸小、成本低，易于制作，易于实现与其他平面器件互联，在一块PCB板上构成一个系统，实现系统的高集成度和小型化。设计SIW滤波器首先根据指标得到谐振频率和耦合系数，再由相关理论得到初始尺寸值，最后在全波仿真软件中不断优化各个尺寸得到需要的滤波器响应。当优化的参数过多时，仿真优化需要较为漫长的过程。由于每次全波仿真耗时长，设计SIW滤波器需要耗费大量的时间。

本文提出一种基于等效电路模型的SIW滤波器快速设计方法，可根据等效电路模型获知当前状态下SIW滤波器实际的谐振频率和耦合系数，进而得知各个尺寸参数的调整方向。采用这种方法只需6次全波仿真即可设计一款工作在21 GHz、带宽为1 GHz的滤波器。

1 基本理论

1.1 SIW谐振腔

图1所示为典型的单层SIW谐振腔。它是由敷于介质基片上下的金属板和嵌入基片的金属化通孔构成的封闭结构，金属通孔的直径为d，孔与孔之间的距离为p。当通孔直径与孔间距满足d<0.2λg，d/p≥0.5时(λg为电磁场在介质中的波长)，电磁场被束缚在其中，向外界泄露能量极低[1]。将单个SIW腔接上输入/输出端口，对其频率响应进行仿真(如图2所示)。SIW腔表现出带通的特性，并且带内插损很低。

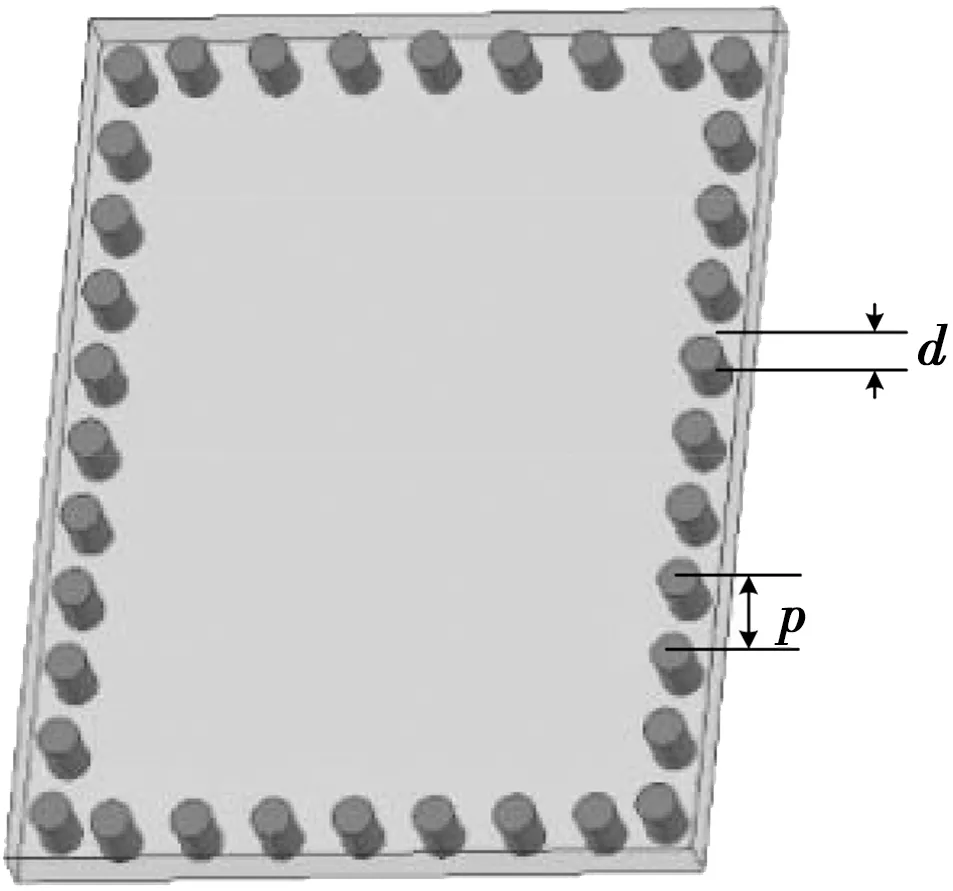
图1 SIW谐振腔

SIW腔与传统矩形波导腔结构、特性都极为相似，已有的矩形波导的设计经验及方法可以直接应用于SIW的设计。对于长为L、宽为W的SIW腔，可以将其等效为一矩形波导，等效出的矩形波导长为Leff， 宽为Weff，两者的尺寸满足如下的关系[2]:

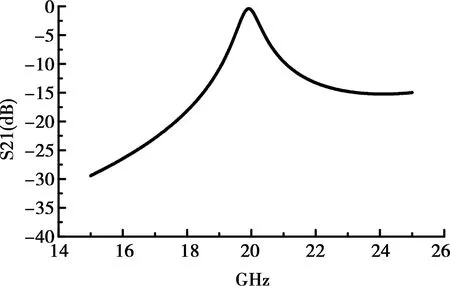
图2 单个SIW谐振腔的频率响应

(1)

(2)

参考矩形波导相关理论[3]，则对于SIW腔中的TEm0n模式(m、n为整数)其谐振频率为

(3)

其中，c0为真空中的光速，εr为介质的介电常数。在实际设计滤波器时，腔体的谐振频率可以用商用软件(如HFSS、CST等)采用本征频率仿真获得。

1.2 耦合系数

现代滤波器设计常用的方法是耦合矩阵法，比较适用于带通滤波器的设计。用这种方法需要知道各个腔的谐振频率、腔与腔之间的耦合系数及外部品质因数[4]。耦合系数是滤波器设计中的重要参数。它定义为耦合能量与存储能量之间的比值。在实际滤波器设计中采用成熟的商业软件提取耦合系数，在软件中建立双腔模型，利用软件的本征模分析可得到电路频率响应中两个谐振峰所对应的两个频率，分别为f1和f2，则耦合系数可以由下式计算：

(4)

此种方法提取的耦合系数只能得出绝对数值，至于该耦合是负耦合还是正耦合需要设计者通过腔的结构加以判断。

1.3 等效电路

SIW谐振腔可用LC并联谐振电路进行等效，如图3(a)所示，其中f代表谐振腔的中心频率。耦合窗可用移相器进行等效，如图3(b)所示，其中k是耦合窗的耦合系数。

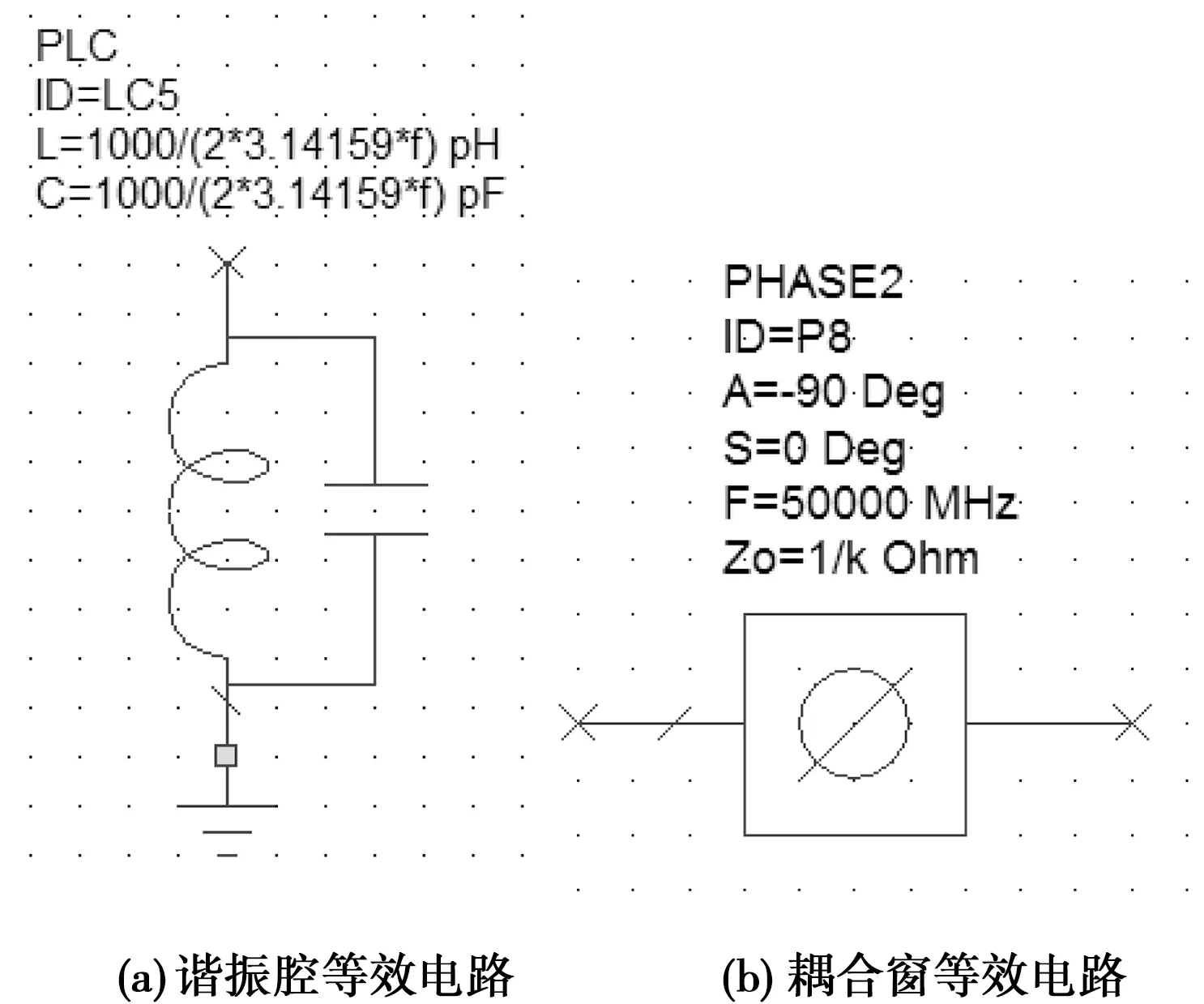
图3 AWR仿真软件中的等效电路

2 六阶SIW滤波器设计

2.1 滤波器结构

所要设计的六阶级联型SIW滤波器的拓扑结构如图4所示。该滤波器左右结构对称。所用的介质基片为Rogers RT/Duroid 5 880，介质的介电常数为2.2，损耗角正切为0.0009，厚度选为0.508 mm，金属通孔的直径为0.4 mm，孔间距设为0.8 mm。

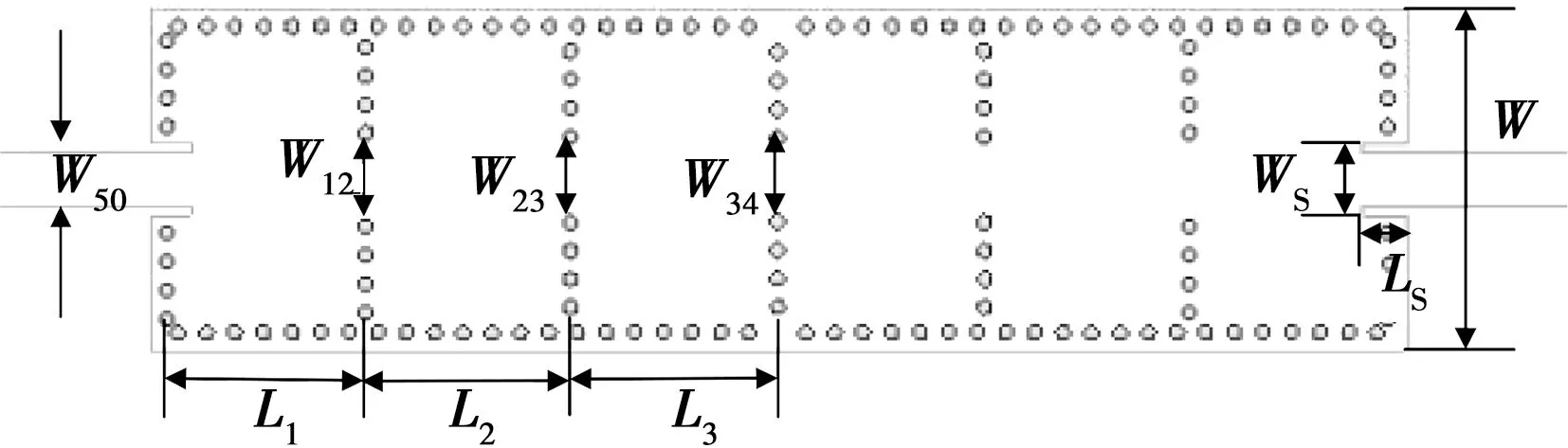
图4 六阶SIW滤波器几何结构

与滤波器对应的电路级模型如图5所示。该模型共有7个优化参数，分别是3个谐振频率、3个耦合系数、1个外部品质因数。

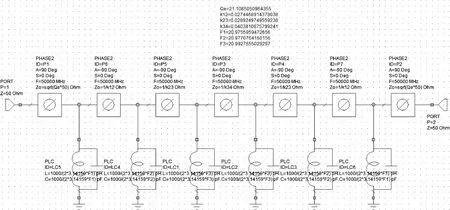
图5 SIW滤波器电路模型

设图4所示的滤波器全波仿真的传输系数和反射系数分别为S21F、S11F。图5所示的等效模型的传输系数为S21C。图5为理想模型，没有考虑各种损耗。由全波仿真结果可以计算实际滤波器的损耗为

D=10*lg(|S21F|2+|S11F|2)

(5)

设理想电路模型和全波仿真的传输系数误差为ε，则

ε=10*lg(|S21C|2)-10*lg(|S21F|2)+D

(6)

优化等效电路模型的7个参数以使ε尽可能小，使电路级的响应与实际全波仿真响应相一致。得出的7个参数值即为实际滤波器当前尺寸参数下各谐振频率、耦合系数的值。为达到预定的值，需要优化滤波器的尺寸。

2.2 滤波器设计

设定滤波器的中心频率为21 GHz，带宽1 GHz，带内反射系数小于-20 dB。根据以上指标，可综合出所需的耦合矩阵[5]，其中一个可能的解是

(7)

耦合矩阵M意味着各个腔体的谐振频率如下：

f1=f2=f3=f4=f5=f6=21 GHz

(8)

以及各个腔体之间的耦合系数和外部品质因数：

k12=k56=0.04，k23=k45=0.029

k34=0.0278， QE=20.91

(9)

图4中的滤波器各尺寸初始值设置如表1所示。

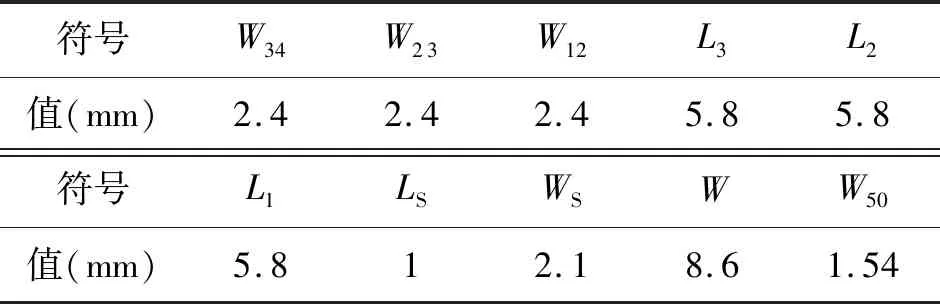
表1 SIW滤波器尺寸初值

对该滤波器进行全波仿真，并优化等效电路模型的参数，使两者响应相一致。全波仿真与等效电路响应如图6所示，两者有较好的吻合度。此时，等效电路的7个参数值如表2所示。

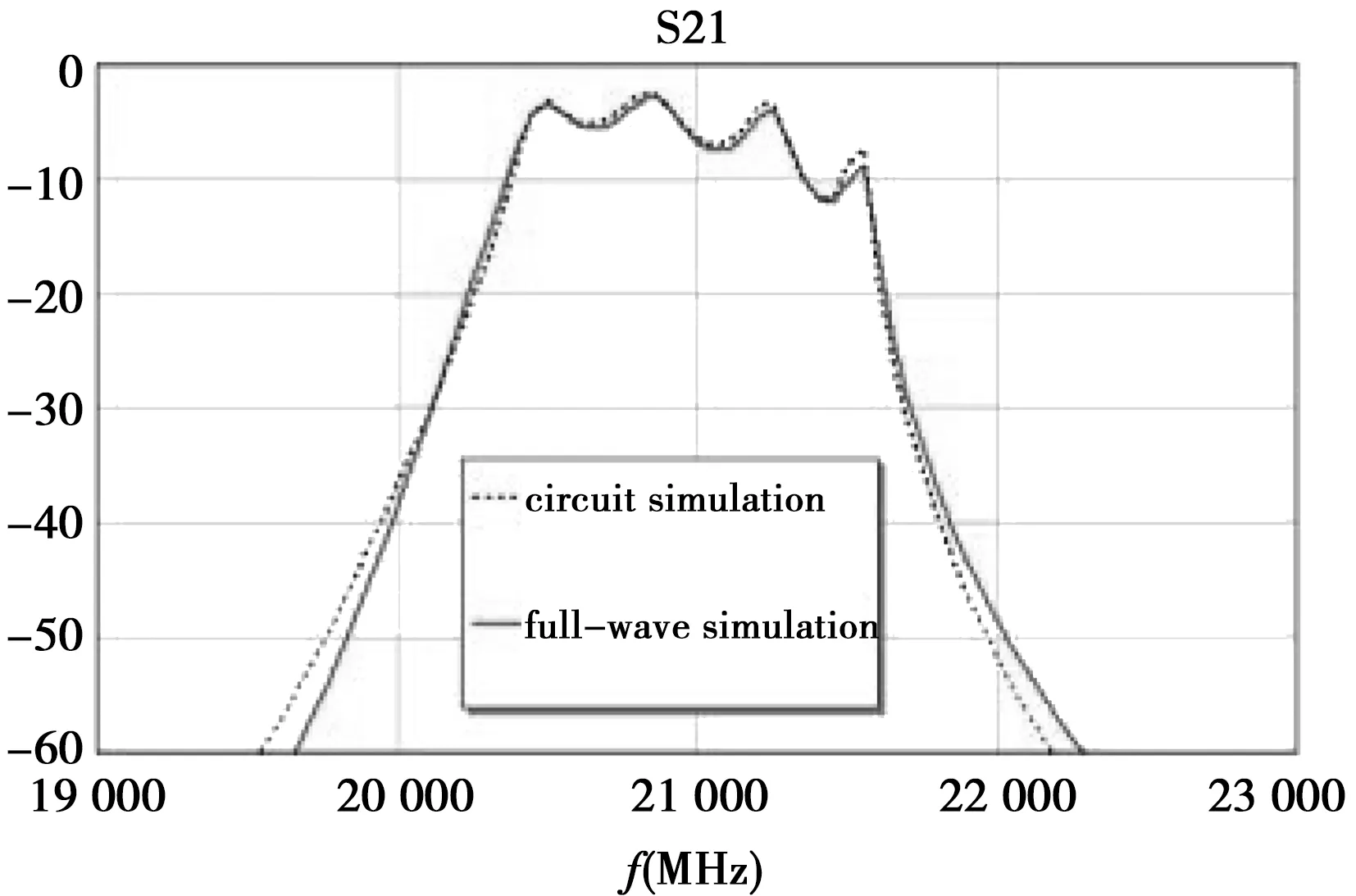
图6 全波仿真与电路模型响应对比

表2 滤波器对应的谐振频率、耦合系数

将表2数据与式(8)、(9)进行对比可知，6个腔的谐振频率都偏小，需要减小腔的尺寸，可主要通过减小L1、L2、L3的值实现。腔1与腔2之间的耦合系数偏小，需要增大W12的值；腔2与腔3、腔3与腔3之间的耦合系数偏大，需要减小W23、W34的值。谐振腔的谐振频率主要取决于腔的尺寸，但也会受到耦合窗大小的影响。耦合系数主要取决于耦合窗大小，但腔尺寸变化会引起耦合系数微小变化。整个滤波器设计过程是一个不断迭代、反复优化的过程。

3 滤波器优化过程

滤波器优化是一个迭代的过程，如图7所示。

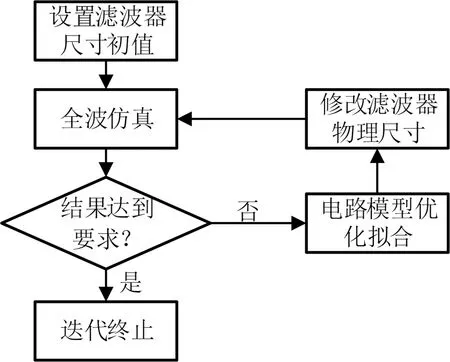
图7 滤波器优化过程流程图

该设计过程把耗时的全波仿真优化转化为快速的电路级优化，一共进行了6次全波仿真即可得到性能良好的SIW滤波器。滤波器物理尺寸变化如表3所示。图4中的WS、W、W50在优化过程中不作变动。

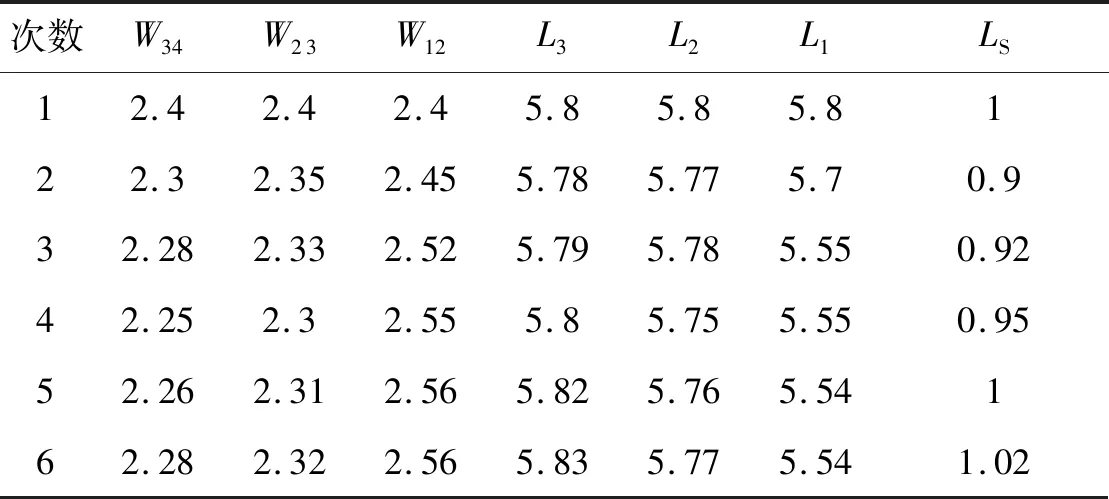
表3 滤波器尺寸变化过程

在优化过程中，图5中的电路模型参数的变化过程如表4所示。

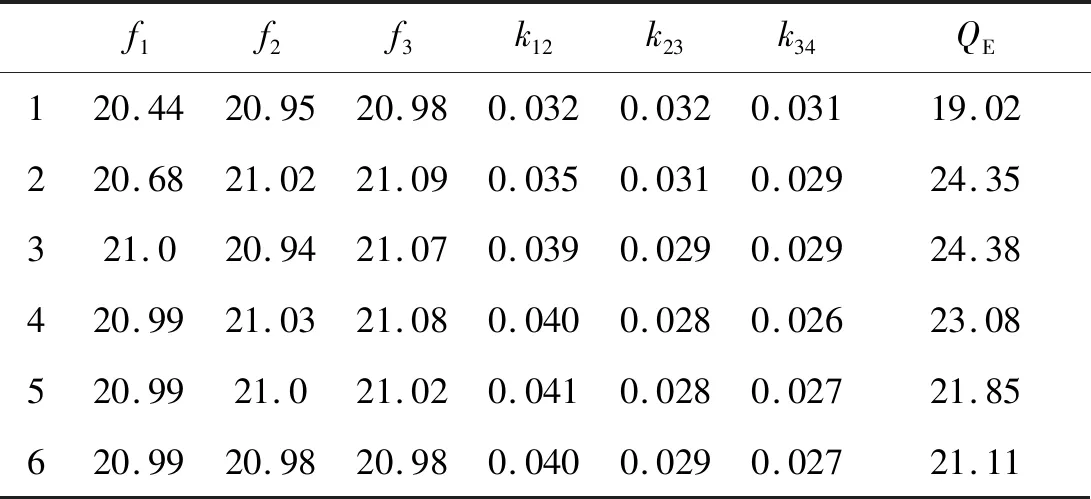
表4 电路模型参数变化过程

第6次仿真后，电路模型参数与式(8)、(9)所示的理论值已经非常接近，此时SIW滤波器的频率响应如图8所示。由图可知，此时的滤波器性能已经十分良好，无需作进一步优化。

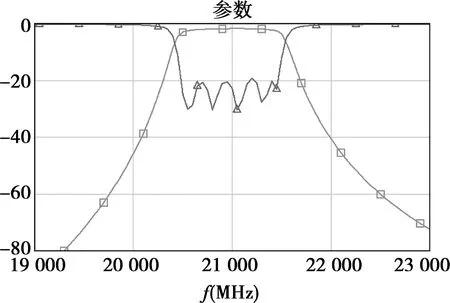
图8 SIW滤波器仿真结果

4 结束语

本文采用快速设计方法设计了一个中心频率为21 GHz、带宽1 GHz的六阶SIW滤波器。通过在AWR仿真软件中建立SIW滤波器的等效电路模型，将耗时的全波仿真优化转化快速的电路级优化，只需6次全波仿真即可得到性能良好的滤波器。