导数测试题A卷

■河南省太康县第一高级中学

一、选择题

1.已知函数f(x)=2 lnx+8x+1,则的值为( )。

A.1 0 B.-1 0 C.-2 0 D.2 0

2.函数f(x)=(2 ex)2+sinx的导数是( )。

A.f'(x)=4 ex+cosx

B.f'(x)=4 ex-cosx

C.f'(x)=8 e2x+cosx

D.f'(x)=8 e2x-cosx

3.曲线y=2 sinx+cosx在点(π,-1)处的切线方程为( )。

A.x-y-π-1=0

B.2x-y-2 π-1=0

C.2x+y-2 π+1=0

D.x+y-π+1=0

4.若x=-2是函数f(x)=(x2+a x-1)ex-1的极值点,则f(x)的极小值为( )。

A.-1 B.-2 e-3C.5 e-3D.1

5.若函数f(x)=a x2+1的图像上在点(1,f(1))处的切线平行于直线y=2x+1,则a=( )。

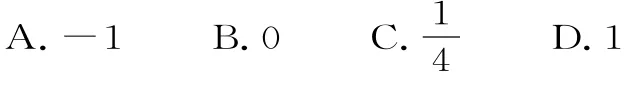
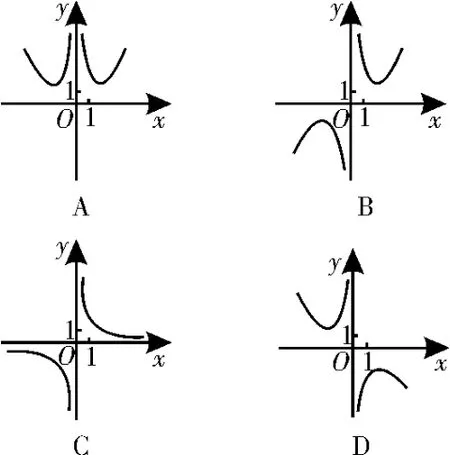
图1

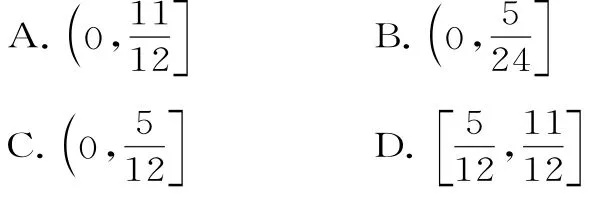
8.设函数f(x)在R上可导,导函数为f'(x),y=(x-1)f'(x)的图像,如图2所示,则( )。

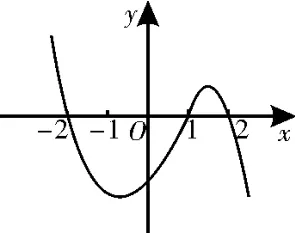
图2

A.f(x)有极大值f(2),极小值f(1)

B.f(x)有极大值f(-2),极小值f(1)

C.f(x)有极大值f(2),极小值f(-2)

D.f(x)有极大值f(-2),极小值f(2)

9.设f'(x)是奇函数f(x)(x∈R)的导函数,且f(2)=0,当x＞0时,有x f'(x)-2f(x)＞0,则使得f(x)＜0成立的x的取值范围是( )。

A.(-∞,-2)∪(-2,0)

B.(-2,0)∪(2,+∞)

C.(-∞,-2)∪(0,2)

D.(0,2)∪(2,+∞)

10.已知f1(x)=cosx,f2(x)=f'1(x),f3(x)=f'2(x),f4(x)=f'3(x),…,fn(x)=f'n-1(x),则f2019(x)等于( )。

11.已知a≠0,函数f(x)=aex,g(x)=ealnx+b,e为自然对数的底数,若存在一条直线与曲线y=f(x)和y=g(x)均相切,则的取值范围为( )。

12.已知函数f(x)=,若存在实数x,使得g(m)-f(x)=1 8成立,则实数m的取值范围为( )。

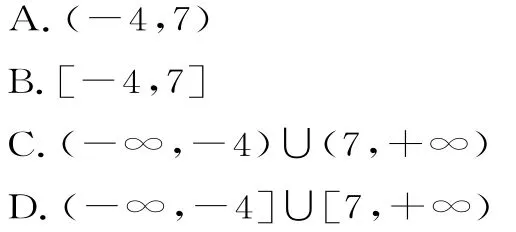
二、填空题

13.已知函数f(x)的导函数为f'(x),且满足,则f(x)=____,其单调增区间为____。

14.已知函数f(x)=m x2+lnx-2x在定义域内存在单调递减区间,则实数m的取值范围是____。

15.已知函数f(x)=记f(0)=m,则f(x)+m＞0的解集为____。

16.已知定义在(-∞,0)∪(0,+∞)上的偶函数f(x)的导函数为f'(x),对定义域内的任意x,都有2f(x)+x f'(x)＜2成立,则使得x2f(x)-4f(2)＜x2-4成立的x的取值范围为____。

三、解答题

(1)当k=2时,求y=f(x)在x=1处的切线方程;

18.已知函数f(x)=-x3+a x2+b x+c(a,b,c∈R),且f'(-1)=f'(3)=0。

(1)求a,b的值;

(2)若函数f(x)在区间[-2,2]上的最大值为2 0,求它在该区间上的最小值。

19.已知函数f(x)=aex-sinx+1,其中a∈R,e为自然对数的底数。

(1)当a=1时,证明:对于任意的x∈[0,+∞),有f(x)≥2恒成立;

(2)若函数f(x)在[0,π]上存在两个不同的零点,求实数a的取值范围。

20.已知函数f(x)=(1+a)x2-lnxa+1。

(1)讨论函数f(x)的单调性;

(2)若a＜1,求证:当x＞0时,函数y=x f(x)的图像恒在函数y=lnx+(1+a)·x3-x2的图像上方。