基于Copula函数的日含沙量随机模拟

张继鹏，彭 杨，时玉龙，赵晓东，丁梦霞

(1.华北电力大学 可再生能源学院，北京 102206；2.华北水利水电大学 水利学院，郑州 450045)

0 引 言

含沙量是一个主要的河流特征变量，综合反映河流的径流与输沙特性。含沙量变化直接影响水库泥沙淤积、河道冲淤、水质及水生环境，因此含沙量随机模拟对流域水沙调控、水质与水环境管理等方面具有重要意义。

自回归模型和解集模型是目前常用的水文随机模型[1,2]，但这两类模型的共同点是采用线性函数关系描述水文现象[3]，难以反映水文时间序列复杂的非线性特征。近年来非线性、非参数随机模型成为水文随机模拟研究的热点，提出了非线性自回归模型[4,5]、人工神经网络模型[6,7]、基于核密度估计的非参数随机模型[3,8]以及非参数解集模型[9,10]等，为水文非线性时间序列模拟提供了多种途径。水文非线性时间序列模拟的核心问题是描述时间序列相邻时段的非线性关系。Copula函数是一种描述变量相关关系的有效方法，由于其对变量的边缘分布没有限制，构造联合分布较为灵活，目前已广泛应用于水文多变量分析中，如洪水频率[11,12]、降雨频率[13,14]、干旱特征分析[15,16]、洪水遭遇[17-19]等。相比较而言，Copula函数在水文随机模拟的应用成果不多，且主要集中在降雨[20]、径流[21,22]和洪水[23]等方面。迄今为止，还未见到Copula函数应用于日含沙量时间序列的随机模拟。因此，本文将采用Copula函数来描述相邻两日含沙量之间的相关结构，在此基础上建立了日含沙量随机模拟模型，并将该模型应用于长江屏山水文站日含沙量过程的随机模拟中。

1 基于Copula函数的日含沙量随机模拟模型

1.1 Copula函数

Copula函数是定义域为[0,1]的多维联合分布函数。依据Sklar定理[24]，一个二维联合分布函数可以由两个独立的边缘分布函数和一个Copula连接函数组成，即

F(x,y)=Cθ[FX(x),FY(y)]=Cθ(u,v)

(1)

式中：Cθ为Copula函数；θ为Copula函数的参数，u=FX(x)，v=FY(y)分别为随机变量X和Y的边缘分布。

Copula函数分为椭圆型、二次型和Archimedean型三大类，其中Archimedean Copula函数结构相对简单，计算方便，可以构造出多种形式、适应性强的组合变量联合分布函数，在水文领域中应用最多。常见的二维Archimedean Copula主要有[24,25]：

(1)Gumbel-Hougaard (GH)Copula函数。

(2)

(2)Clayton Copula函数。

C(u,v)=(u-θ+v-θ-1)-1/θ,θ∈(0,∞)

(3)

(3)Frank Copula函数。

(4)

(4)Ali-Mikhail-Haq (AMH)Copula函数。

(5)

1.2 相邻两日含沙量联合分布

根据式(1)，相邻两日含沙量的联合分布可表示为：

FS(st,st-1)=Cθt[Fst(st),FSt-1(st-1)]=Cθt(ut,ut-1)

(6)

式中：st-1和st分别为第t-1日和第t日的含沙量；FS(st,st-1)为st-1和st的联合分布；ut-1=FSt-1(st-1)和ut=FSt(st)分别为st-1和st的边缘分布；θt为第t日的Copula函数的参数，根据相关性指标法[25]，可利用其与Kendall秩相关系数τ之间的关系求出；第t日的Kendall秩相关系数τt采用下式计算：

(7)

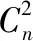
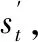
1.3 基于条件分布的随机模拟模型

根据式(1)，第t日的含沙量st的条件分布可表示为：

(8)

式中：Gθt(ut,ut-1)为条件Copula函数。由此可得到基于Copula函数的日含沙量随机模拟模型，即：

(9)

根据式(9)就可以实现对 的随机模拟，具体步骤如下：

(1)采用正态分位数变换法对实测含沙量数据进行标准正态化；

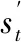
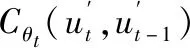
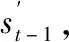
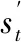
2 实例应用

选取金沙江下游屏山站1955-2010年共56年的实测日含沙量资料作为建模的基本资料，采用所建模型对屏山站日含沙量进行随机模拟。屏山站是金沙江干流出口控制站，流域控制面积458 592 km2，多年平均径流量1 460 亿m3，多年平均输沙量2.39 亿t，多年平均含沙量1.66 kg/m3。为简化计算，模拟时每年2月份均取28 d。

2.1 日含沙量联合分布建立

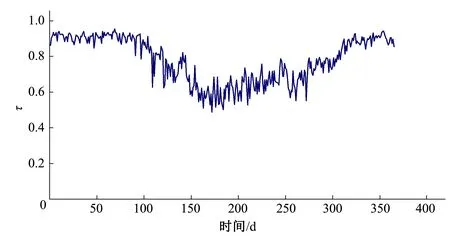
图1 各日与的秩相关系数Fig.1 Daily rank correlation coefficients of

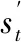
(10)

式中：Pei，Pi分别为经验联合频率和理论联合频率；i和n分别为样本序号和样本容量。

各日的OLS值与对应的最优Copula函数分别如图2和图3所示。由图2可见，在一年内，OLS值的最大值为0.025 1，最小值为0.008 1，平均值为0.013 7，说明所选定的二维Copula联合分布计算出的理论联合分布概率与经验频率拟合较好。图4给出了屏山站日OLS值接近平均值时联合分布的经验概率与理论概率的拟合情况，从图4中可以看出，二者拟合情况较为理想。

2.2 日含沙量的模拟及检验

采用上述模型对屏山站日含沙量过程进行了长序列模拟，模拟了100组与实测样本容量(56 a)相等的日含沙量序列，并对模拟结果进行检验。

图2 各日OLS值Fig.2 Daily OLS values

图3 各日最优Copula函数Fig.3 Daily best-fit copula functions

图4 经验与理论联合概率对比Fig.4 Comparison of empirical and theoretical joint probabilities

图5 屏山站模拟与实测序列各日统计参数Fig.5 Simulated and measured statistics of daily sediment concentrations in the Pingshan station

图5给出了屏山站实测和模拟含沙量序列各日统计参数，即均值、标准差Sd、变差系数Cv、偏态系数Cs以及滞时为1的秩相关系数τ。表1统计了屏山站日含沙量模拟序列各日统计参数绝对误差和相对误差的平均值以及相对误差≤10%的通过率。由图5和表1可见，模拟序列各日的统计参数与实测序列吻合较好，各统计参数的通过率均在98%以上，最大平均相对误差4.22%，其中均值和秩相关系数τ的通过率均达到100%，最大相对误差分别为0.83%和0.49%。因此，基于二维Copula函数的屏山站日含沙量过程随机模拟结果能够反映实测日含沙量序列的统计特征，模拟精度也较高。

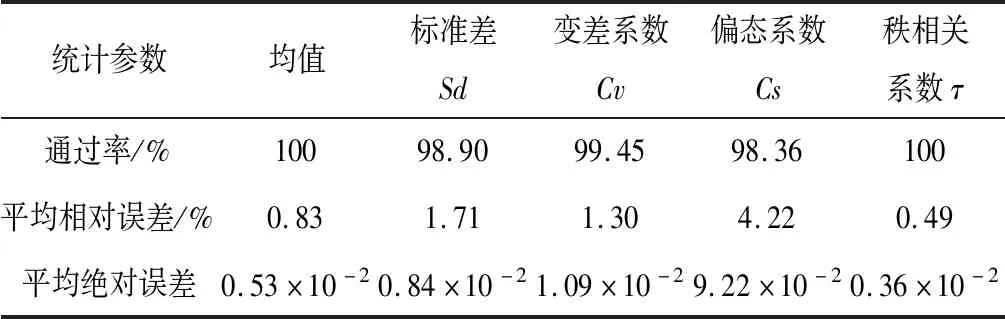
表1 各统计参数通过率及平均相对误差Tab.1 Passing rate and average relative error of statistical parameters

2.3 与其他模型比较

为进一步说明本文所建模型的模拟效果，本文还将模拟结果与分期平稳AR模型的模拟结果进行比较。表2给出这两种模型的日含沙量模拟序列各统计参数与实测序列的相对均方根误差RMSE[27,28]，其中RMSE采用下式计算：

(11)

式中：δo,j为实测序列第j日的统计参数；δs,j为模拟序列第j日的统计参数；m为总日数。式(11)表明，RMSE值越小，模拟序列与实测序列之间的拟合程度越好。

由表2可见，基于Copula函数的日含沙量模拟的均值和Cv值对应的RMSE值与分期平稳AR模型的基本一致，但Sd、Cs和τ值对应的RMSE值明显小于分期平稳AR模型，表示基于Copula函数的日含沙量模拟序列在偏态性和非线性相关关系方面明显优于分期平稳AR模型。因此，与分期平稳AR模型相比，基于Copula函数的日含沙量模拟序列的拟合结果基本一致，但在偏态性和非线性相关关系方面具有明显的优势。

表2 两种模型统计参数RMSE值比较Tab.2 Comparison of RMSE values of statistical parameters in two models

3 结 论

本文考虑相邻两日含沙量之间的相关性，建立了基于Copula函数的日含沙量随机模拟模型。针对日含沙量模拟时段较多，日含沙量边缘分布难以统一确定的特点，采用正态分位数变换对实测含沙量资料进行了标准正态化处理。将该模型应用到金沙江下游屏山站日含沙量随机模拟，并将计算结果与分期平稳AR模型计算结果进行比较，结果表明，本文所建模型能较好地保持实测日含沙量资料的统计特性，模拟精度较高，模拟序列的均值，标准差，变差系数，偏态系数以及秩相关系数τ的通过率均在98%以上，平均相对误差最大不超过4.5%，且在偏态性和非线性相关关系方面优于分期平稳AR模型，说明本文所建模型可用于随机模拟长序列日含沙量过程，并能为其他水文资料的长序列模拟方法提供参考。