基于BP、Elman、PSO-SVR三种预报模型在石羊河流域的应用比较

雷 莉，王 超

(1.甘肃省石羊河流域水资源局，甘肃 武威 733000；2.中国水利水电科学研究院，北京 100038)

0 引 言

石羊河是甘肃省河西走廊水系第三大河，分布在我国西北干旱半干旱地区，常年降水量较少，蒸发量大。近年来，伴随着工农业生产的迅速发展，如何完成水资源的优化配置和水量调度，以满足各用水单位或部门的需求，是首要解决的问题。而具有高精度的中长期径流预报可为流域水资源的精细化分配和合理开发利用提供可靠的依据。因此，开展中长期水文预报在石羊河流域应用的研究，对于解决石羊河流域需水量增加和水资源供需矛盾加剧等问题具有重大而深远的现实意义。

传统的中长期径流预测方法包括时间序列法[1]，多元线性回归法[2]，逐步回归法[3]等。然而传统的方法往往很难达到理想的预报效果，随着信息技术和数学理论的不断发展进步，出现了新的中长期预报方法，例如人工神经网络法[4]，灰色系统方法[5]，小波分析法[6]，混沌理论方法[7]，支持向量机方法[8]，最优组合预测方法[9]等。其中，人工神经网络法以其较强学习能力和高效的运算机制等，被广泛应用于中长期径流预报并具有较高的预报精度。纪昌明、俞洪杰[10]等采用基于互信息的预报因子集优选方法，并耦合BP人工神经网络对雅砻江流域沪宁水文站进行预测，与现有方法相比，模型预测的准确性得到了很大提高。屈亚玲和周建中[11]提出了一种改进的Elman神经网络模型，并将其应用于中长期径流预报。与未改进的Elman神经网络模型相比，预报精度得到显著提高；支持向量机由于其强大的鲁棒性和泛化能力而被广泛应用于中长期径流预测。在赣江流域[12]的实例研究表明，运用主成分分析法筛选预报因子，能够缓解预报因子间信息重叠导致“过拟合”问题，可以使人工神经网络模型在率定期和检验期的预测精度得到显著。

大量研究发现，由于每个地区的水文，气象和人类活动不同，下游模型不适用于所有流域。因此，通过综合分析流域特征，气候条件和模型适用条件等因素，选择预测模型可为流域提供高精度的预测结果。因此，本文引入130项大气环流指数，并基于主成分分析筛选预测因子法构建BP，Elman和PSO-SVR的中长期径流预报模型被用作石羊河流域的中长期径流预报模型。通过对不同模型预测结果的比较分析，选择适合石羊河流域的中长期径流预报模型，为石羊河流域中长期径流预报提供技术支持。

1 模型原理和方法

1.1 主成分分析法

主成分分析[13](PCA)是一种多变量统计方法，其中用于导出的少量主成分包含原始变量中的大部分信息。并且每个主成分的信息彼此不相关。从而达到简化数据和降维的目的。

设初始变量的指标和新的综合指标分别为x1,x2,…,xp，z1,z2,…,zp(m≤p)则主成分分析原理表示为(1)：

(1)

式中：z1,z2,…,zp为x1,x2,…,xp所对应的m个主成分；系数l矩阵L为荷载矩阵。其中，zi与zj(i≠j)相互无关；z1为x1,x2,…,xp的线性组合，同时，方差在所有线性组合中最大，z2是与z1不相关的x1,x2,…,xp的线性组合且方差在所有线性组合中最大，依次类推。

1.2 BP人工神经网络模型原理

BP人工神经网络[14](反向传播神经网络)(Back Propagation Neural Network)是1986年由Rumelhart和McCelland为首的科学家小组提出，它是一个多层的前馈型神经网络模型。BP神经网络可以根据预测误差连续调整网络各层的权重，从而达到预测输出无限接近预期输出的效果。具有三层结构的BP人工神经网络由于具有很强的映射能力，所以被广泛应用于各大水文预报领域中。其模型拓扑结构包括输入层(input layer)、隐层(hide layer)和输出层(output layer)，如图1所示。

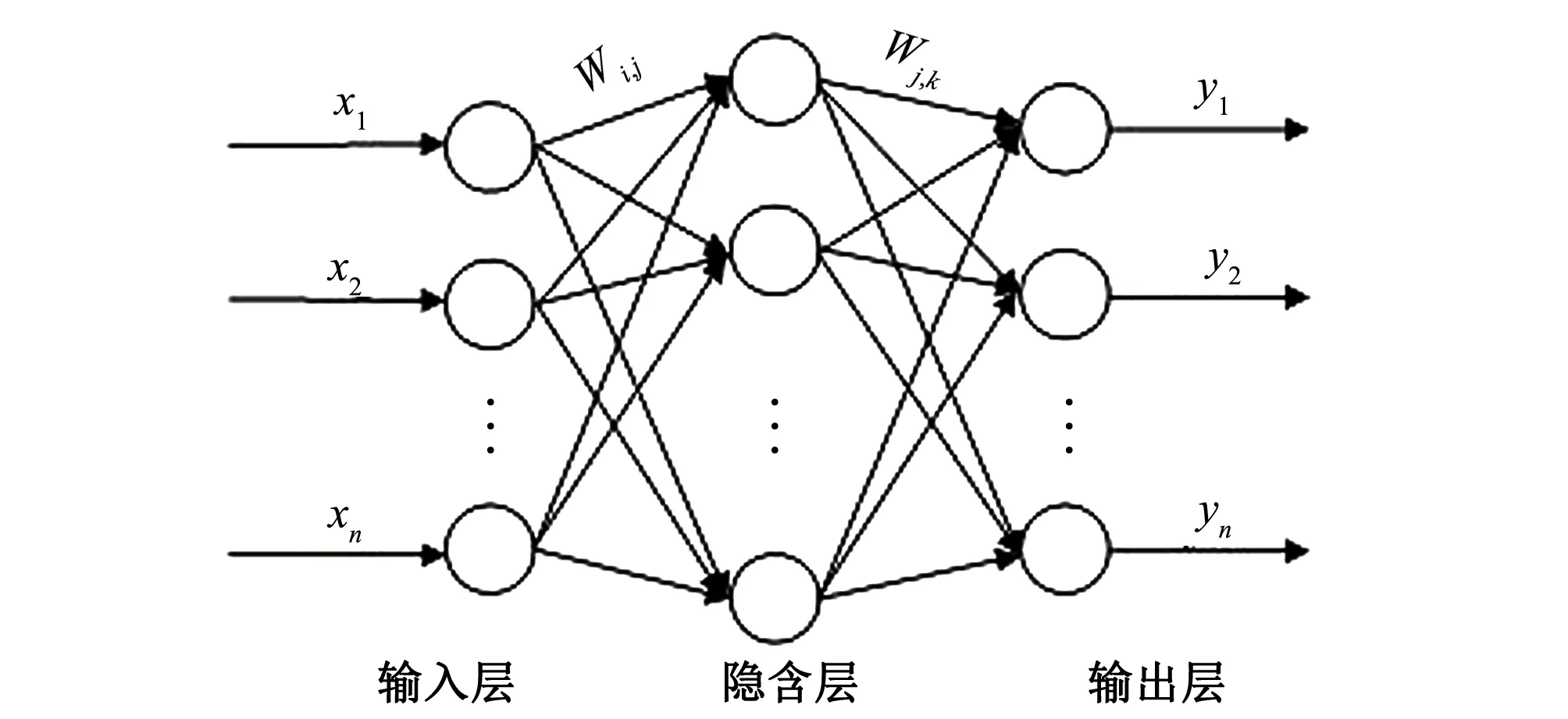
图1 BP人工神经网络结构概化图

当BP神经网络模型运行时，隐含的节点(n)的数量在模型的准确性中起决定性的作用，其确定方式如下：

(2)

n=log2m

(3)

(4)

式中：n为隐含层节点数；m为输入层节点数；l为输出层节点数；α为[1,10]的整数。

在这三种方法中确定隐含层节点数的最大值和最小值，然后从最小值进行试算，直到最大值，n被选择为输出和预期结果之间具有最小误差的隐含层节点的数量。

1.3 Elman神经网络模型原理

Elman神经网络是J.L.Elman于1990年提出来的，Elman神经网络是一种典型的局部回归网络(global feed forward local recurrent)。即一个将局部记忆单元和局部反馈连接组合在一起的前项神经网络。

Elman网络的前馈连接结构类似于BP神经网络结构，包括输入层，隐含层和输出层，可以学习和修正其连接权；反馈连接具有固定的连接权重，其“结构”单元可以记住前一时刻的输出值。在Elman神经网络中，除了与BP神经网络相同的隐含层外，还存在连接到隐含层的节点和接收器反馈信号的关联层(或联系单元层)。类似于状态反馈，关联层的主要功能是使用局部记忆单元同时连接前一时刻的输入和当前时刻的输入作为隐含层的输入。隐藏层的传递函数仍使用某种非线性函数，一般是Sigmoid函数；输出层和关联层都是线性函数。相应网络结构图如图2所示。

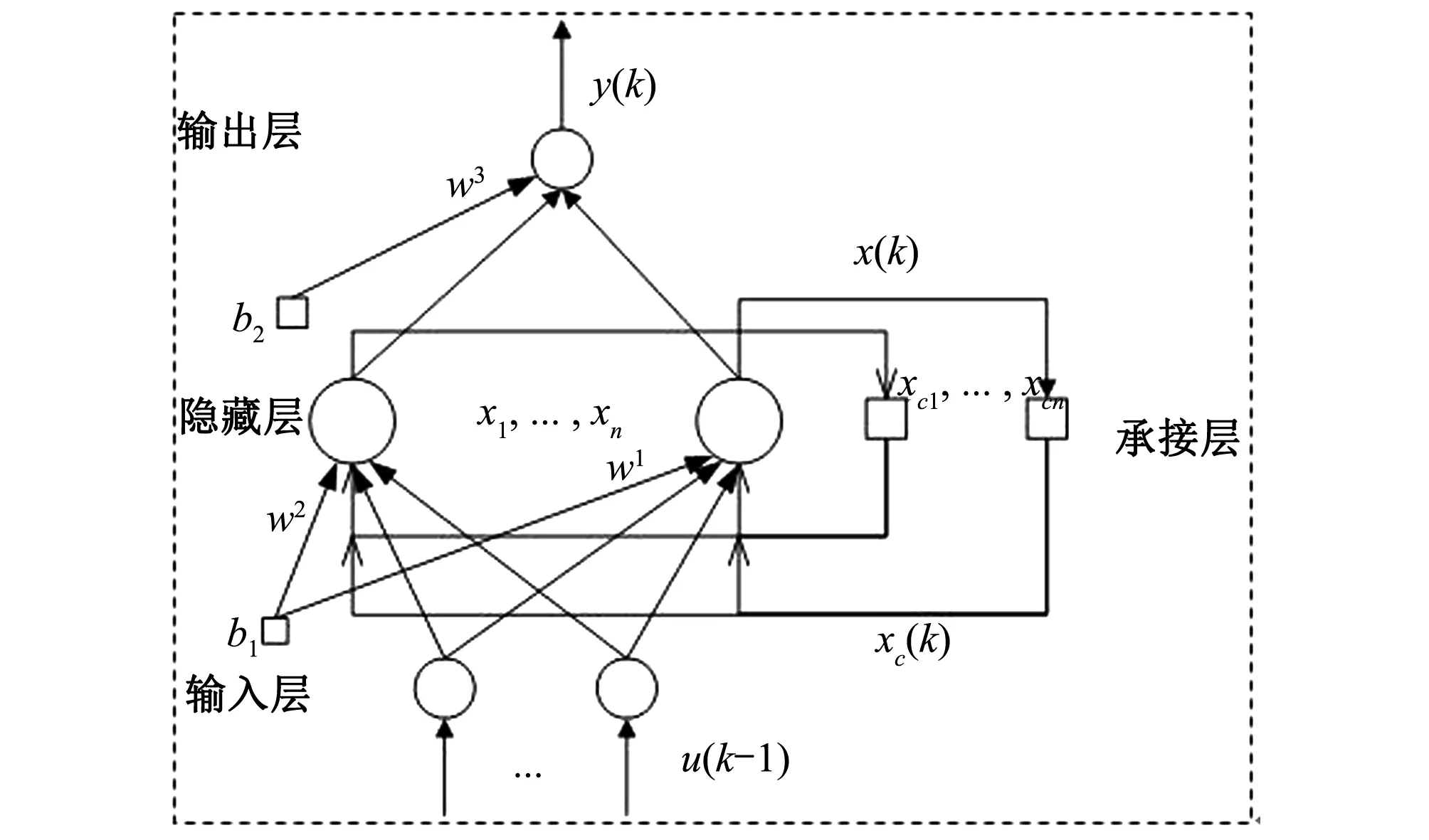
图2 Elman神经网络结构图

Elman神经网络模型增加了结构层到输出层的连接权系数，以达到提高网络性能的目的。Elman神经网络模型主要将连接权重矩阵从输入层传递给隐含层，结构单元传递给隐含层和隐含层传递给输出层，通过输出单元和隐层单元所组成的非线性向量函数确定隐层的节点数。

1.4 PSO-SVR模型原理

支持向量机(SVM)作为一种新兴的机器学习方法最早由Vapnik[15]和其他人在20世纪90年代中期提出的。支持向量机以统计学习的VC维理论为理论基础，以结构风险最小化原理为目标。支持向量机主要用于解决分类和回归预测问题。与其他回归算法相比，回归支持向量机(SVR)非常适用于小样本和非线性问题的回归预测。SVR的基本思想是利用核函数将低维非线性问题转化为高维线性问题，并利用线性方法求解高维特征空间中的非线性问题。通过多次试验，SVR在解决回归预测问题方面具有较高的可信度和良好的泛化能力。

在实际应用中，惩罚系数C，核参数σ和不敏感损失系数ε的选择对模型的性能有很大影响。并且三个参数的赋值存在诸如计算量大和难以获得最佳值的问题。目前很多文章中采用网格搜索法确定这三个参数值，网格搜索方法是通过组合网格搜索和交叉验证来确定参数值。该方法计算量大，易于陷入局部最优解，导致预测精度低。因此，粒子群优化算法(PSO)取代了网格搜索法来选择参数，因为PSO算法具有易于实现，收敛速度快，全局搜索能力强等优点。因此，粒子群优化算法在SVR模型的参数优化中具有一定的优势。

2 模型的应用

2.1 研究区概况

石羊河流域总面积4.16 万km2，产流面积1.1 万km2，多年平均径流量15.6 亿m3(流域降雨和径流主要集中在5月至9月。分别占全年的76%和64%以上)；由于石羊河流域处于我国干旱和半干旱地区，故流域主要以大气降雨(雨季)和高山冰雪融化为主。同时，近年来石羊河流域出现枯水期频发的缺水、供需矛盾加剧等问题，而水库的合理优化调度正是解决流域缺水、供需失衡等问题的关键所在，中长期径流预报可为水资源的优化配置提供可靠的技术支持。因此，本文以西营水库作为研究对象，研究西营水库入库径流的中长期预报模型。

2.2 径流特性分析

选取1970年至2016年西营水库年径流量序列进行统计分析。径流的年际变化由径流极值比Km和变化系数Cv描述。Km和Cv越大，径流的年际变化越大；反之，径流年际变化越小。西营水库年径流变异系数计算为0.17，径流年际极值比为2.05。Cv和Km值均较小，表明年径流的年际变化较小，不同年份的径流分配相对稳定，总体确实略显平缓。径流的变化过程见图3。

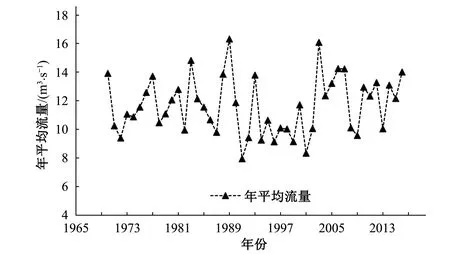
图3 西营水库1970-2016年径流变化过程

2.3 实例应用

选择石羊河流域西营水库1970年至2016年整编的月入库径流数据作为本次预报的数据来源。本次研究的径流数据自1970年至2016年，共47年，时间系列相对较长，符合中长期径流预报对数据的要求。

首先，选择中国气象局国家气候中心气候监测办公室(http:∥cmdp.ncc-cma.net/Monitoring/cn_index_130.php)提供的130项气候系统指数(即88个大气环流指数，26个海温指数和16个其他指数)作为候选因子。采用相关系数法用于计算每个候选因子与年平均径流序列之间的相关系数，并选择给定可信度α=0.05的显著性检验因子。因子初步选取结果如表1所示。

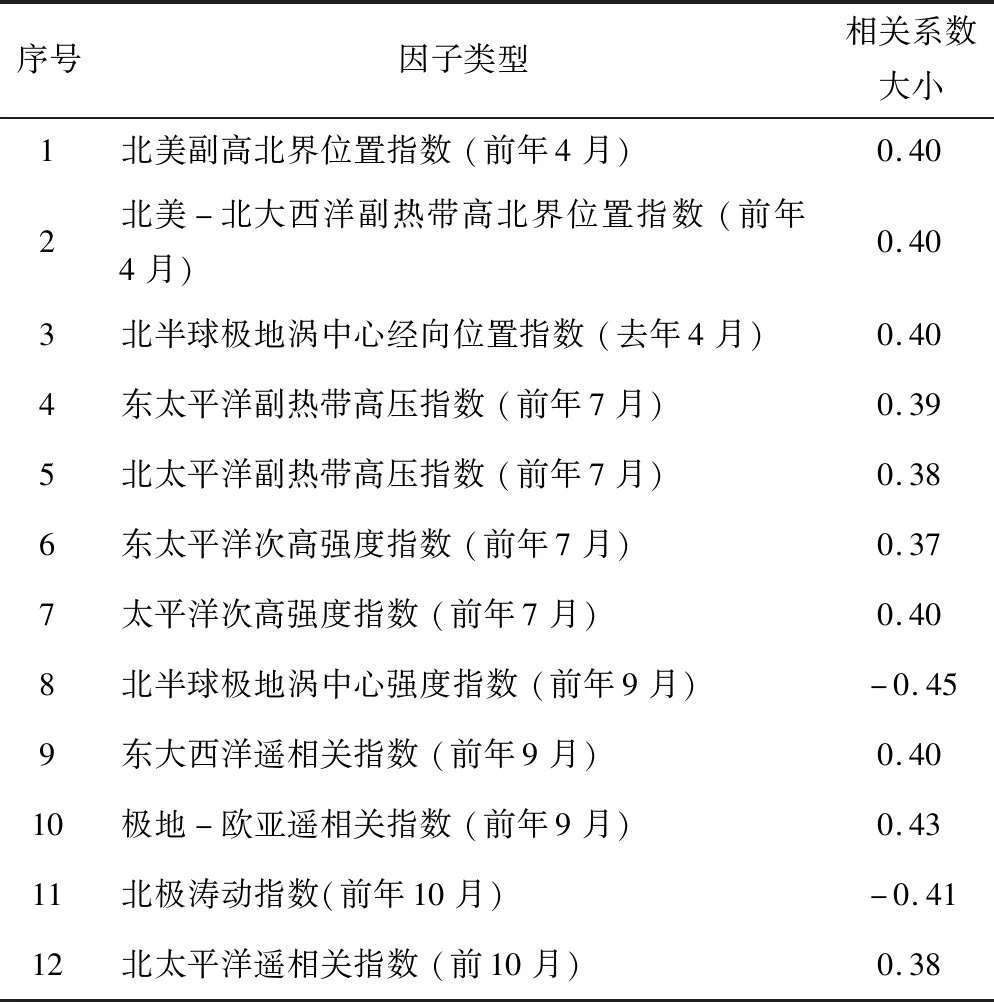
表1 西营水库预报因子初步优化结果

其次，在相关系数法初步选择因子的基础上，通过主成分分析法，采用PCA原则选择满足85%贡献率预测因子组合，主成分分析碎石图和得分系数矩阵如图4、表2所示。将得分系数引入等式(1)产生新的预测因子z1,z2,…,z5作为模型的输入因子。

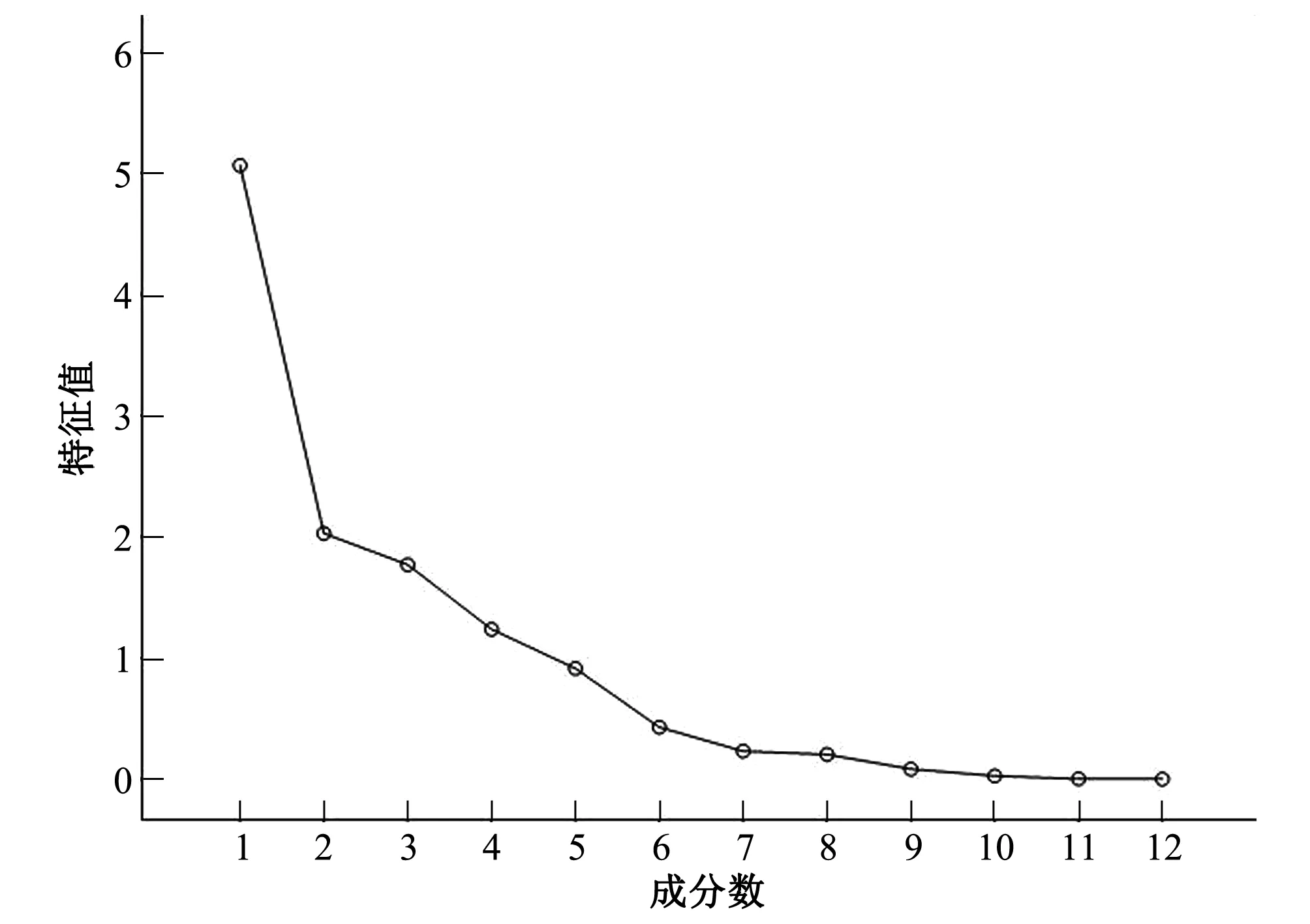
图4 主成分分析碎石图

最后，将主成分分析选取的预测因子分别作为BP，Elman和PSO-SVR模型的输入条件，应用于西营水库年径流的预测。该模型从1970年到2004年被设置为样本的率定样本，并且该模型在2005年至2016年进行检验。通过率QR用作预测准确度的评估指标，《水文情报预报规范》中通过率的定义式为等式(2)。

(5)

在该公式中，M是预测值通过的次数(预测值与实测值之间的相对误差在±20%之间)，N为检验期样本总数。

3 结果与分析

经过整理计算，3种不同模型的预报效果如图5～图7所示，不同模型的参数结构和预报精度评价结果如表3和表4所示。

从表4的统计数据可以看出，径流预报中三种模型在率定期的平均相对误差均小于10%。综合图5～图7可知，预报结果拟合良好；检验期的径流预报平均相对误差均有所增大，其中BP人工神经网络模型的误差增加率最大，说明相比于Elman、PSO-SVR模型，BP人工神经网络预报模型稳定性更差些；三种预测模型总体平均相对误差在20%以内，表明本研究选用BP、Elman、PSO-SVR三种预报模型对西营水库进行预报具有一定的合理性。

三种模型在率定期的预测结果合格率均在90%以上，效果良好。尤其BP神经网络模型的合格率更是达到了100%。然而，BP模型在检验期的合格率仅为75%，表明基于主成分分析筛选预测因子的BP神经网络模型具有过拟合现象，模型可靠性较低；Elman和PSO-SVR模型在检验期的预报合格率均大于80%，分别为83.33%和91.67%。根据《水文情报预报规范》，Elman和PSO-SVR模型的合格率均达到80%，满足预报规范要求，可用于工作预测。

表3 BP、Elman、PSO-SVR模型参数结构

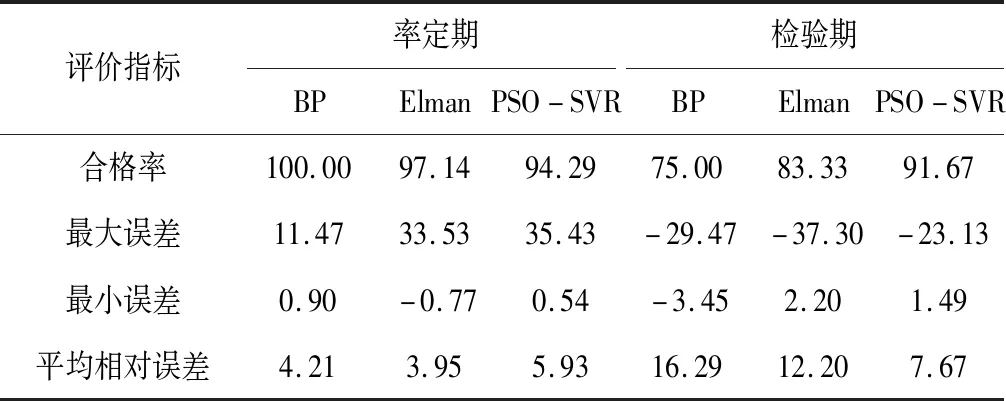
表4 BP、Elman、PSO-SVR年径流预报精度评价结果 %

综合表4和图5～图7的预报效果，相比于BP神经网络模型而言，Elman网络模型的预报精度更高，这表明Elman模型在结构上与关联层连接，增强了模型处理动态信息的能力。而PSO-SVR模型的预报精度和稳定性整体比BP、Elman模型更好些，表明加入PSO算法对参数自动寻优后，SVR模型克服了计算复杂度大，易陷入局部最优等问题，使得模型的更加通用，预报效果更佳。

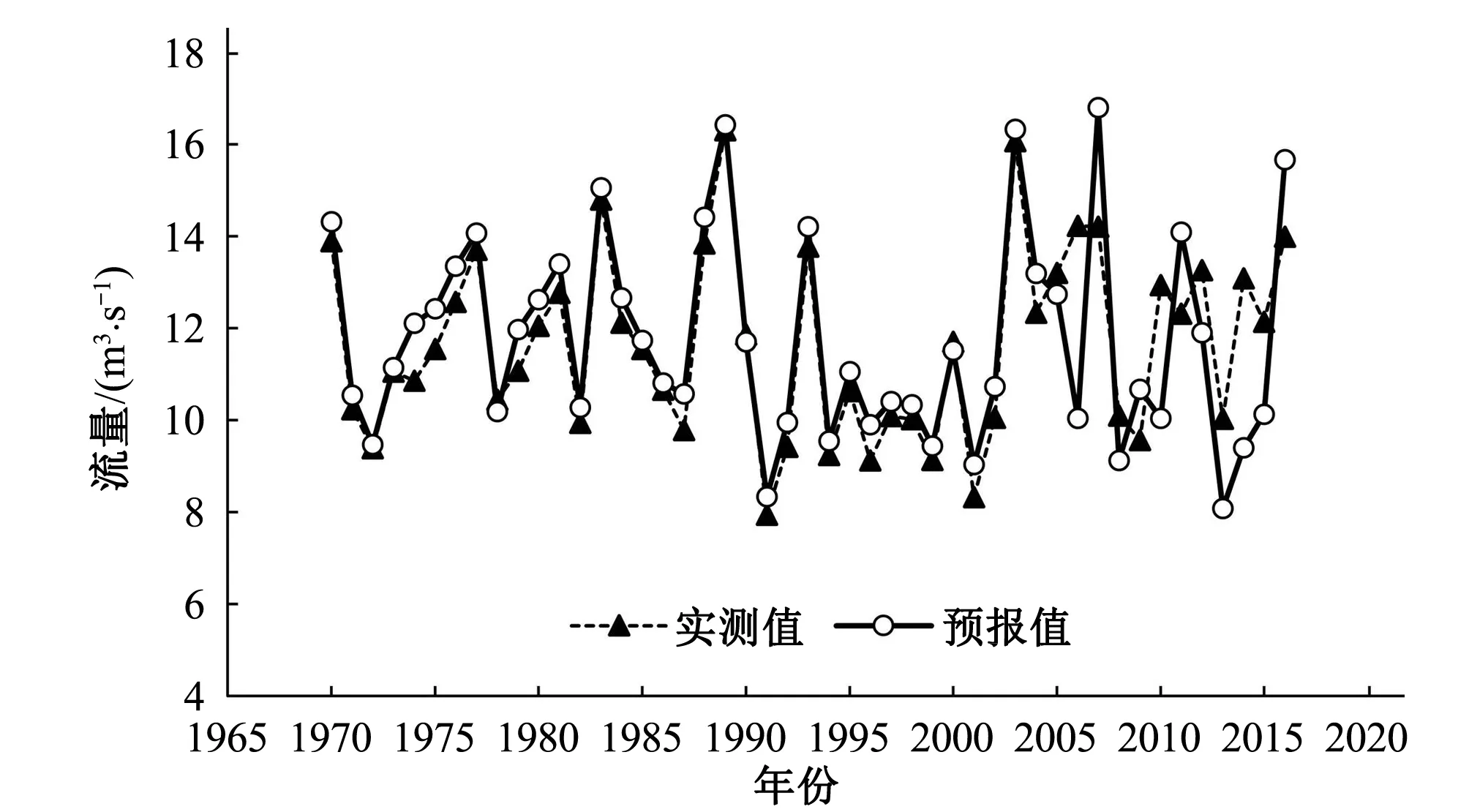
图5 西营水库年径流预报(BP模型)

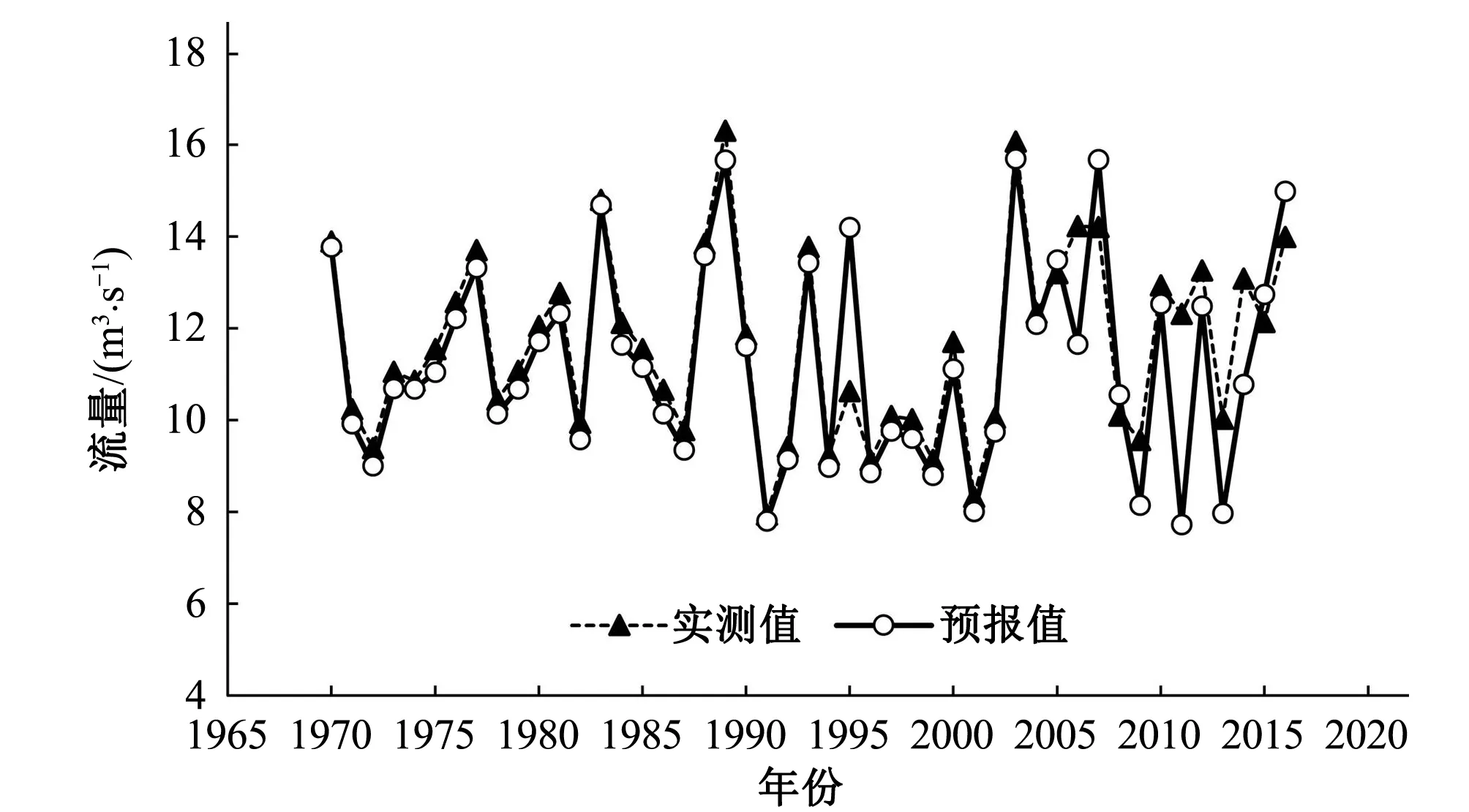
图6 西营水库年径流预报(Elman模型)

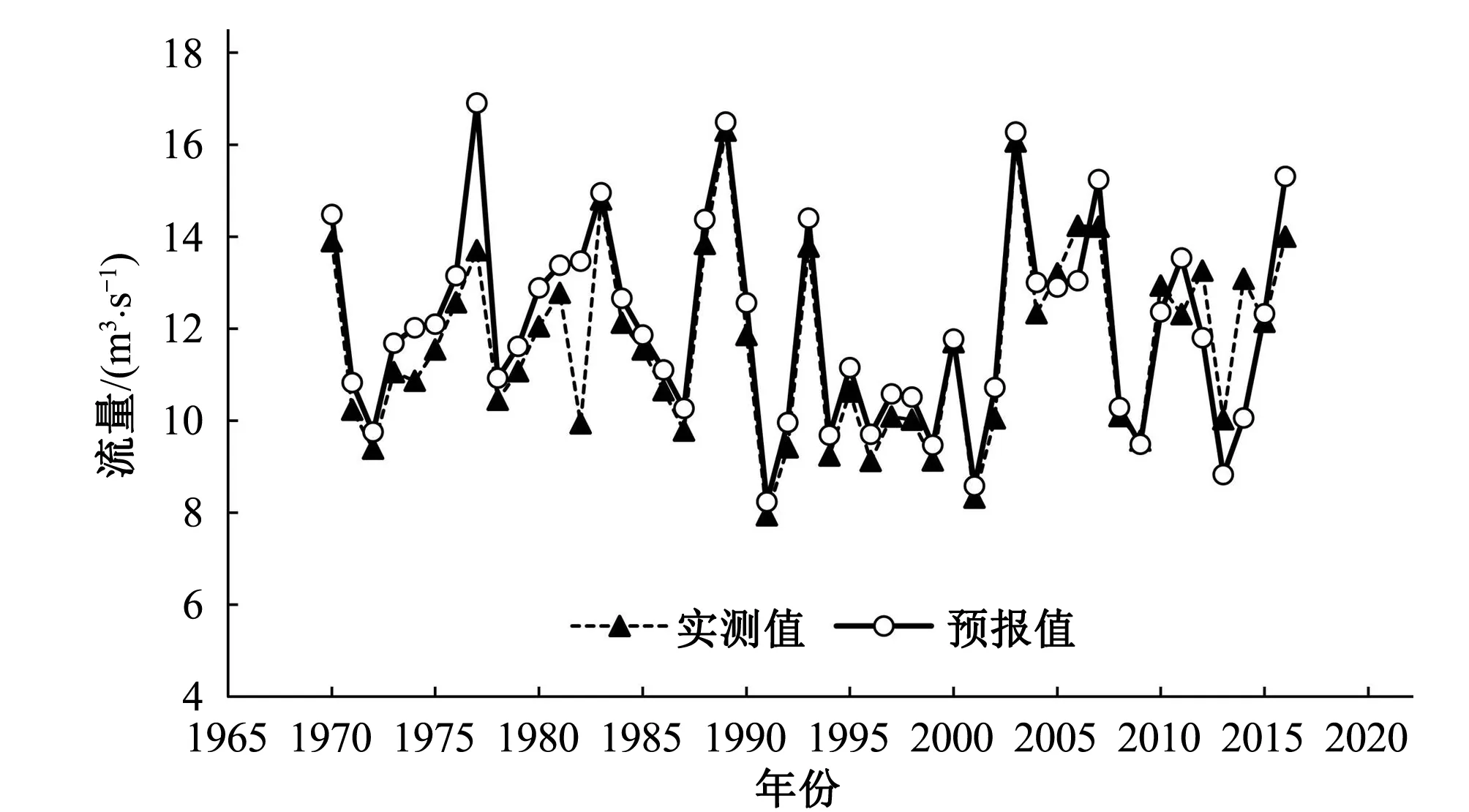
图7 西营水库年径流预报(PSO-SVR模型)

4 结 语

综上所述，为石羊河流域的中长期径流预报工作提供可靠的技术支撑，本文采用可分析多变量间的相关性，去除变量间重叠信息，导出少数主分量，并使其保持原始变量的全部信息以达到简化数据和降维作用的主成分分析方法作为预报因子筛选的方法。基于主成分分析方法的预报因子筛选方法，中长期径流预测模型对BP神经网络模型，Elman神经网络模型和PSO-SVR模型的预测结果进行比较和分析。结果表明，基于主成分分析方法筛选预报因子的Elman神经网络模型和PSO-SVR中长期径流预报模型的预报精度较高，它满足了石羊河流域中长期径流预报的需要。因此，在石羊河流域，基于主成分分析筛选预测因子的Elman神经网络模型和PSO-SVR模型可以作为中长期径流预测的首选模型。甚至在西北内陆河流域的中长期径流预报作业中，该预报模型也可进行推广使用。