等离子体参量的发射光谱诊断的研究
孙殿平
(华东师范大学 a.精密光谱科学与技术国家重点实验室;b.物理与材料科学学院,上海 200062)
1 概 述
等离子体是 “物质第四态”, 已被广泛地应用于激光器、光源照明、能源、物质与材料加工、环保与宇宙科学、化学合成、表面处理、薄膜制备、闪电放电过程研究等诸多领域[1-12]. 因此其电子密度、粒子密度、温度等参量的诊断成为物理学研究的重要课题之一[1,7].
研究等离子体参量有实验诊断、理论解析和数值模拟3种研究手段[13-18]. 由于等离子体中的物理化学过程极其复杂,使得理论解析以及计算机数值模拟很难准确地获得等离子体的各种参量,这就显现了等离子体实验诊断的重要性. 常用的实验诊断手段主要有光学诊断技术、Langmuir探针[19]和质谱技术[13].
光谱学诊断方法是用等离子体的发射光谱或吸收光谱诊断等离子体温度、密度和化学组分等参量的方法[16-17]. 此法是在20世纪50年代初期由H.迈克等人较为系统地提出的[16],起初应用于天体物理和基础实验研究,应用于实验室等离子体最早是从高温聚变等离子体诊断开始的,后来又应用于航天环境模拟、化工冶炼、热加工和能源等方面的实验中.
等离子体发射光谱作为无干扰方法可用于多种等离子体物理特性的诊断,如等离子体的电子温度、电子密度、激发温度甚至某些动力学过程. 针对高温等离子体,其中的连续辐射光谱可用于电子温度的测量[20],线状谱线的Stark效应[21]可以用于电子密度的测量,而线状谱线的强度分布可以用于激发温度的诊断[22]. 针对低温等离子体,上述效应虽然较弱不足以可靠诊断等离子体,但也促进了许多其他技术的发展,高分辨发射光谱的谱线线型分析[23]是等离子体中激发过程动力学机理的一种有效分析手段.
在低温等离子体诊断中,发射光谱学的早期应用主要有两方面,即刻蚀和沉积过程[24]的机理诊断以及非稳态等离子体发光过程的时间行为分析. 瞬态等离子体的非平衡特性明显,重新发展相应的发射光谱诊断技术的分析理论显得十分重要. 例如:利用谱线的Stark展宽测量电子密度的理论模型必须加以修正. 利用谱线的Stark移动测量电场分布[24]的原理也需要改进. 利用分子光谱谱带[25]分析实现温度测量是发射光谱诊断的重要内容,但是瞬态等离子体的非平衡特性使得传统光谱模拟理论方法也必须加以修改.
发射光谱法由于仪器系统简单、选择性好、适用范围广、环境条件要求低,可以作为一种便携式在线无接触诊断方法. 但是由于大量干扰谱峰的存在,在实践中这种方法主要用于简单分子的等离子体诊断.
然而发射光谱的定量分析却是一个难点,发展定量分析的理论和方法是十分必要的. 另外对于不发光物种的诊断是间接的. 可利用吸收光谱技术定量测量不发光物种成分、浓度、温度等参量[26]. 20世纪60年代,开始用激光光谱诊断法对等离子体状态和输运性质进行实验研究[8,27].
2 实验测量装置
常见的发射光谱测量实验装置如图1所示,主要包括2部分:等离子体产生装置和光谱测量装置[8,28].
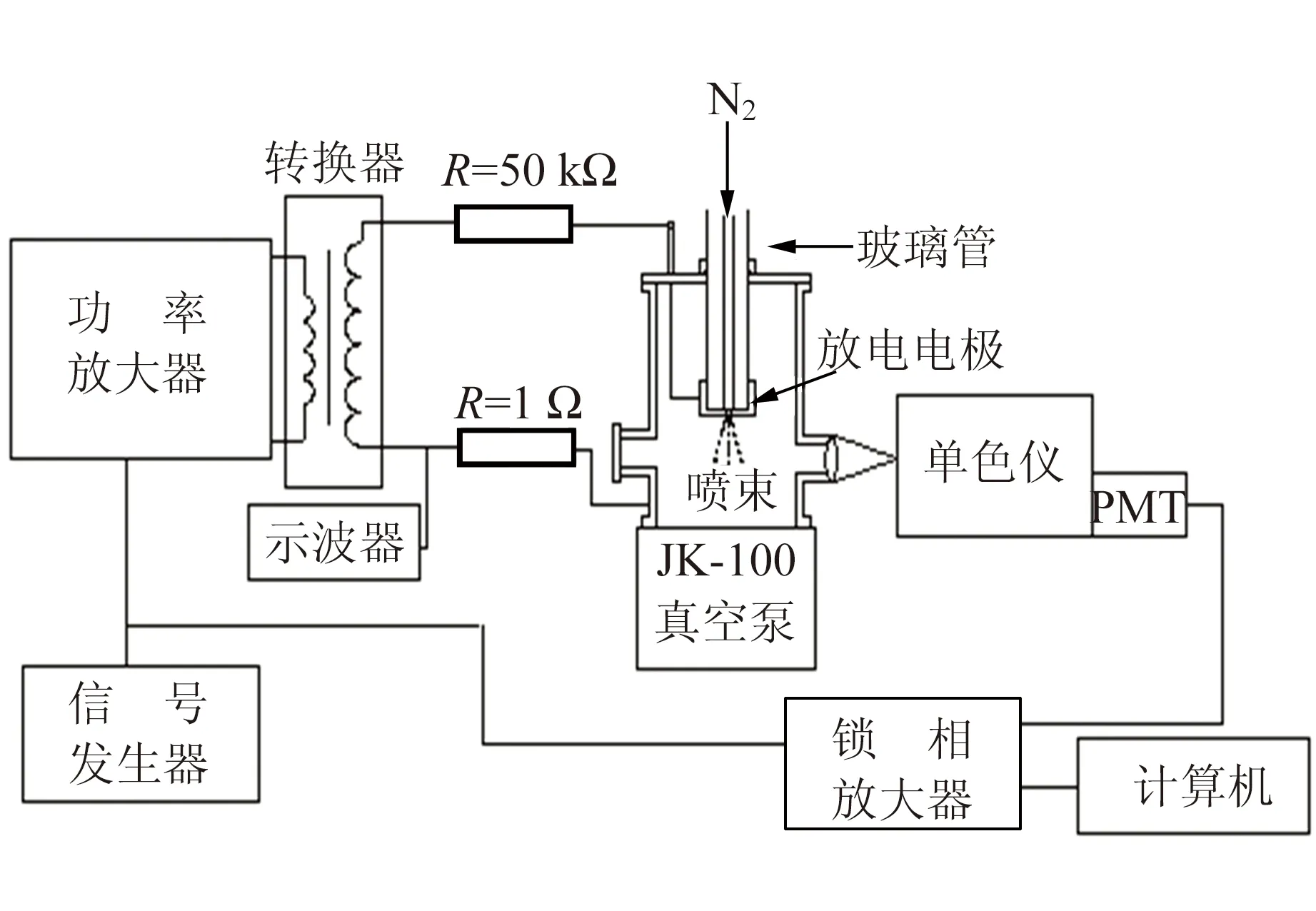
图1 实验装置示意图
交流电压产生等离子体,其气体瞬态分子(如离子分子、自由基分子和激发态分子等)在每个放电周期发生2次浓度的突然变化,因此锁相放大器采用1f参考信号进行解调来获得速度调制光谱,2f参考信号进行解调来获得浓度调制光谱. 探测到的信号经由锁相放大器解调后输送到电脑记录和读取[29]. 它是一种内调制光谱技术,具有很高的灵敏度. 若两电极放电不均匀对称,通过浓度调制光谱分别在1f和2f参考频率上进行测量,可以了解电极的放电强度及氮离子分子产生的微观过程[28,30].
脉冲直流放电技术实验装置如图2所示[31],探测信号经Boxcar 检测采集数据后送入计算机处理,对于脉冲激光产生的等离子体的研究也可采用类似光谱采集系统[31-33]. 通过Boxcar或采用计算机软件控制[34],可以测量等离子体中不同寿命粒子的发射光谱信号的时间演化特性[35-36].
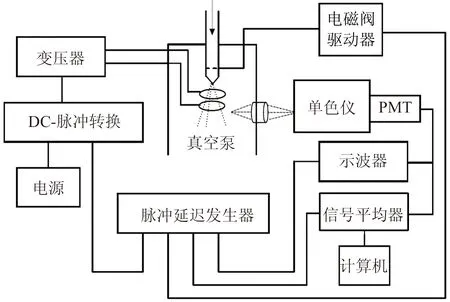
图2 文献[31]中的脉冲直流放电实验装置示意图
3 等离子体参量的发射光谱测量
发射光谱携带着大量的信息:1)光谱线的频率,据此可确定等离子体的激发物种;2)光谱线的强度及强度分布;3)光谱线的线型. 因此原则上利用等离子体的发射光谱能提供诊断等离子体温度、电子密度、激发、电离状态和化学组分及各成分的相对含量等[7],还可以获得分子的转动温度、等离子体的激发温度等重要参量[36-38].
3.1 等离子体的温度及其诊断
在多数情况下,等离子体会偏离局部热力学平衡状态,这样就不能用单一温度描述出等离子体的行为,需区分讨论激发温度、振动温度、转动温度等不同温度的概念. 通常,如果等离子体中每种组分的速率都分别满足1种Maxwell速率分布,针对某种粒子不同类自由度的平均能量就可以定义不同的温度,那么不同的组分就可用不同的温度来描述. 这样等离子体中发生的不同过程就可用不同的温度来表征. 通常的光谱法测温,总是假定等离子体处于局部热力学平衡和光薄状态[36-38].
3.1.1 平动温度
离子、原子的平动能量对应平动温度. 所以平动温度测量可用离子或原子发射谱线的多普勒展宽法测量. 线状谱谱线的多普勒展宽计算平动温度的方法是利用等离子体中的粒子热运动引起的谱线的展宽效应[38-40]. 首先确定谱线的中心波长λ0,然后,确定该波长谱线的宽度Δλ1/2,再用谱线多普勒展宽公式:
(1)
式中,kTa为计算原子的温度,单位是eV,ma和A分别是被测原子的质量和相对原子量,c是真空中的光速.
多普勒展宽测温法只适用于粒子数密度较小、低压、稀薄气体的情况(例如分子束中),谱线加宽主要是由效应引起的.
从式(1)可知,温度愈高,多普勒加宽愈大,而在相同温度下,轻粒子的谱线加宽大于重粒子的,故此法常采用氢谱线作为测量线. 在低温等离子体测温范围内,加宽量很小,仅为0.01~0.000 1 nm,必须用高分辨率光谱仪才能测定.
3.1.2 转动温度
分子气体温度不太高时会激发转动自由度. 转动态分布处于热平衡时,分布在转动状态J的分子数为[37]
(2)
式中,NJ′表示原子、离子或分子处于给定的转动能级的布居数,Be为转动能级的转动常量,N为总粒子数,Ttot即为转动温度. 由于所用单色仪的分辨率不同,得到不同分辨率的发射光谱,因此不同分辨率的转动光谱有对应的不同转动温度测量方法.
1)转动谱线可分辨的高分辨转动光谱
对于转动分辨清晰可见的光谱,P,Q,R支的间距比较大,不必考虑3支的重叠. 根据每条谱线的强度和对应的转动量子数,可以用
(3)
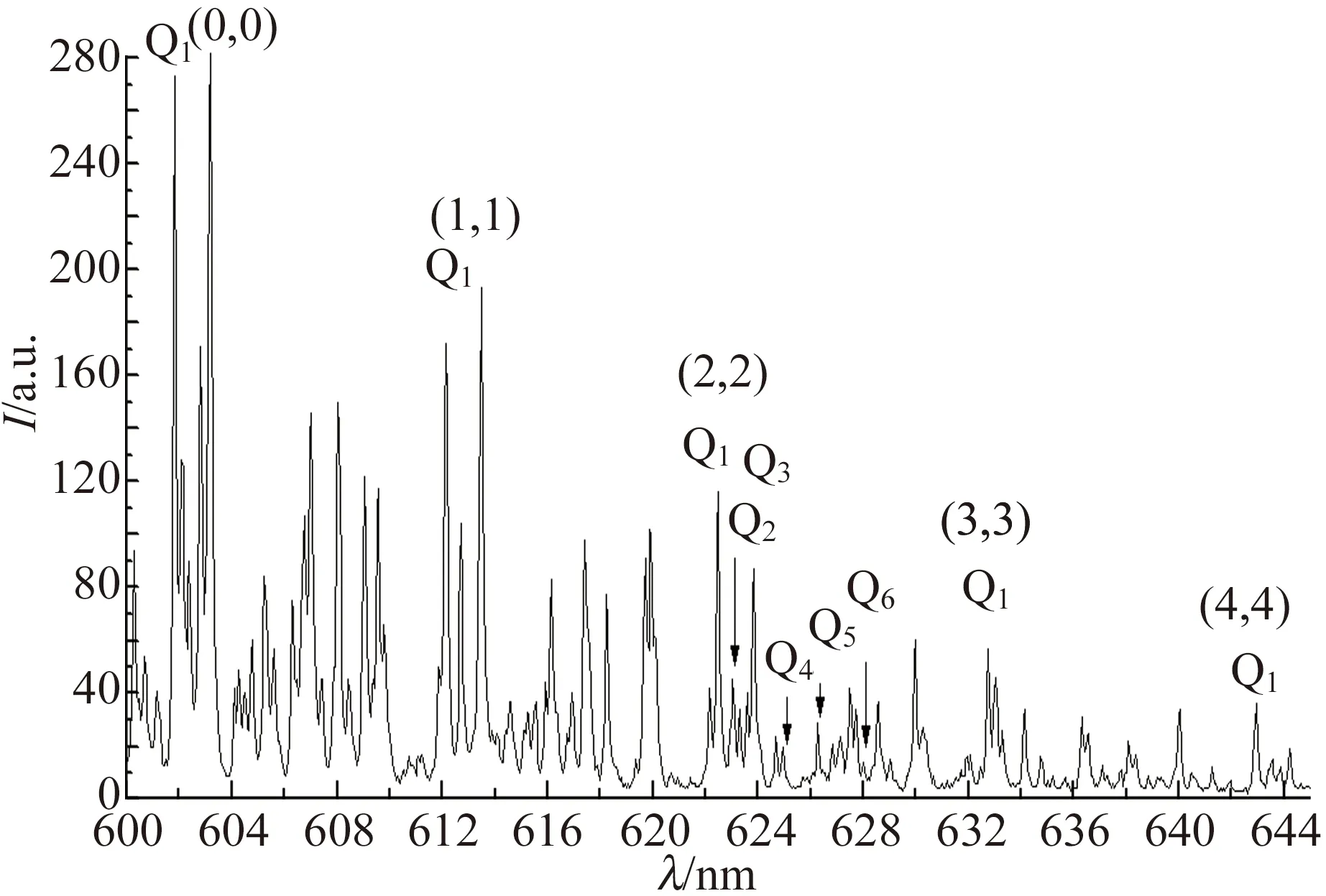
图3 文献[41]中氢分子带的振转结构光谱图

(4)
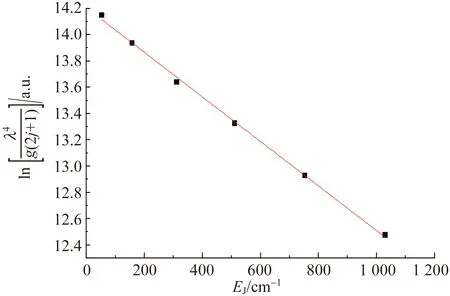
图4 文献[41]中氢分子放电Fulcher-α带(2,2)Q支发射光谱的玻尔兹曼曲线
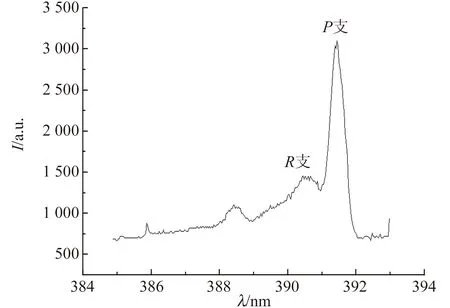
图5 文献[30]喷束中的电子态(0,0)振动带跃迁谱线
3)P支和R支不可分辨的转动光谱带
对P,Q和R支有重叠,特别是三重态的跃迁,如CO转动谱线(如图6所示)[8],各支重叠严重,很难分辨. 对于这样的谱带,可编写程序进行模拟,通过与实验谱线相比,可以得到转动温度.
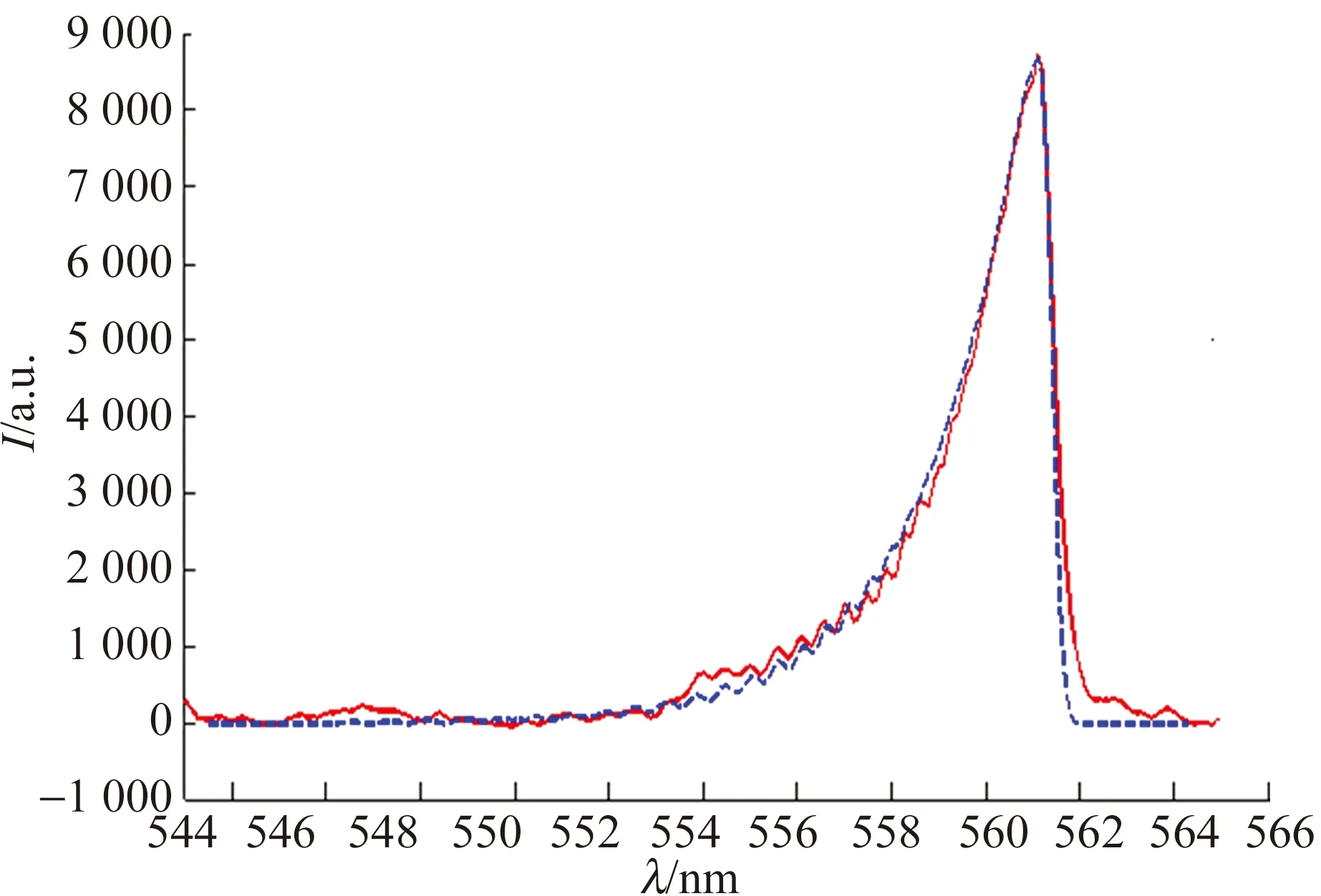
图6 文献[8]中CO B1∑→A1Π(0,3)发射光谱与转动温度在450 K时的发射光谱模拟
在放电体系中,激发态的形成有2种机制:一种电子碰撞激发,另一种是反应形成. 对于电子碰撞激发过程中,分子角动量是守恒的,因此由NJ′可以推测下能级的转动态分布情况,而反应生成激发态的过程分析则相当复杂.
3.1.3 振动温度
在同一电子态的不同振动态v中的粒子数Nv为[8,37]
(5)
式中,Qv为配分函数,Tv即为振动温度,G(v)为振动能量. 等离子体中分子的振动温度不受重视,但有学者[42]认为通过增强等离子体的振动激发,反应物将易于吸附到催化剂上,并能有效克服反应势垒,使能耗降低,因此分子的振动温度在化学合成中成为一个重要参量.
1)谱线可分辨振动谱的振动温度
由于振动函数是归一化的,对v的前进组带,所以在一般情况下,同一电子态的振动跃迁中,电子跃迁矩Re为常量,可得[8]:
(6)
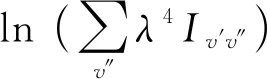
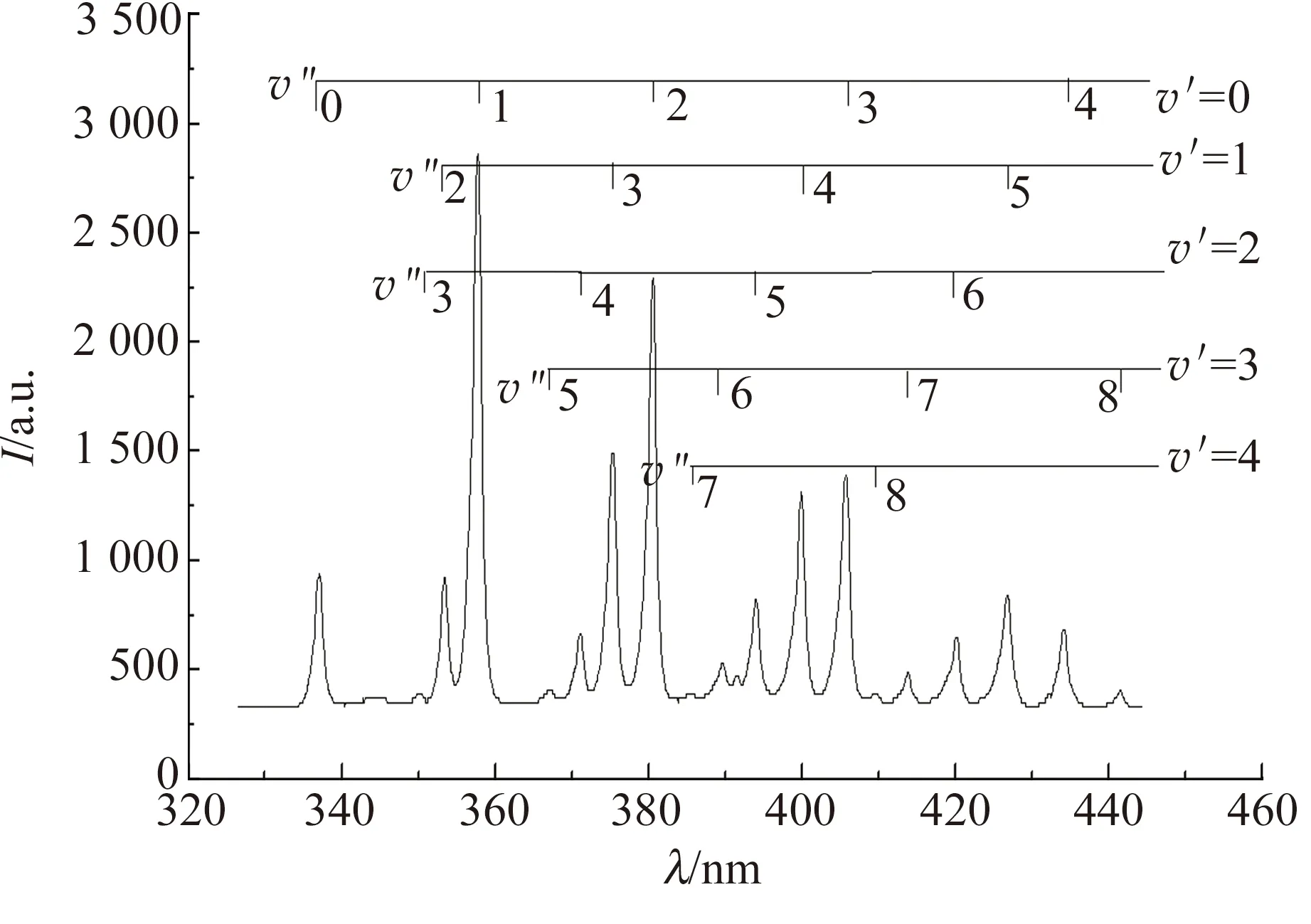
(a) 玻璃管中探测到的N2发射光谱
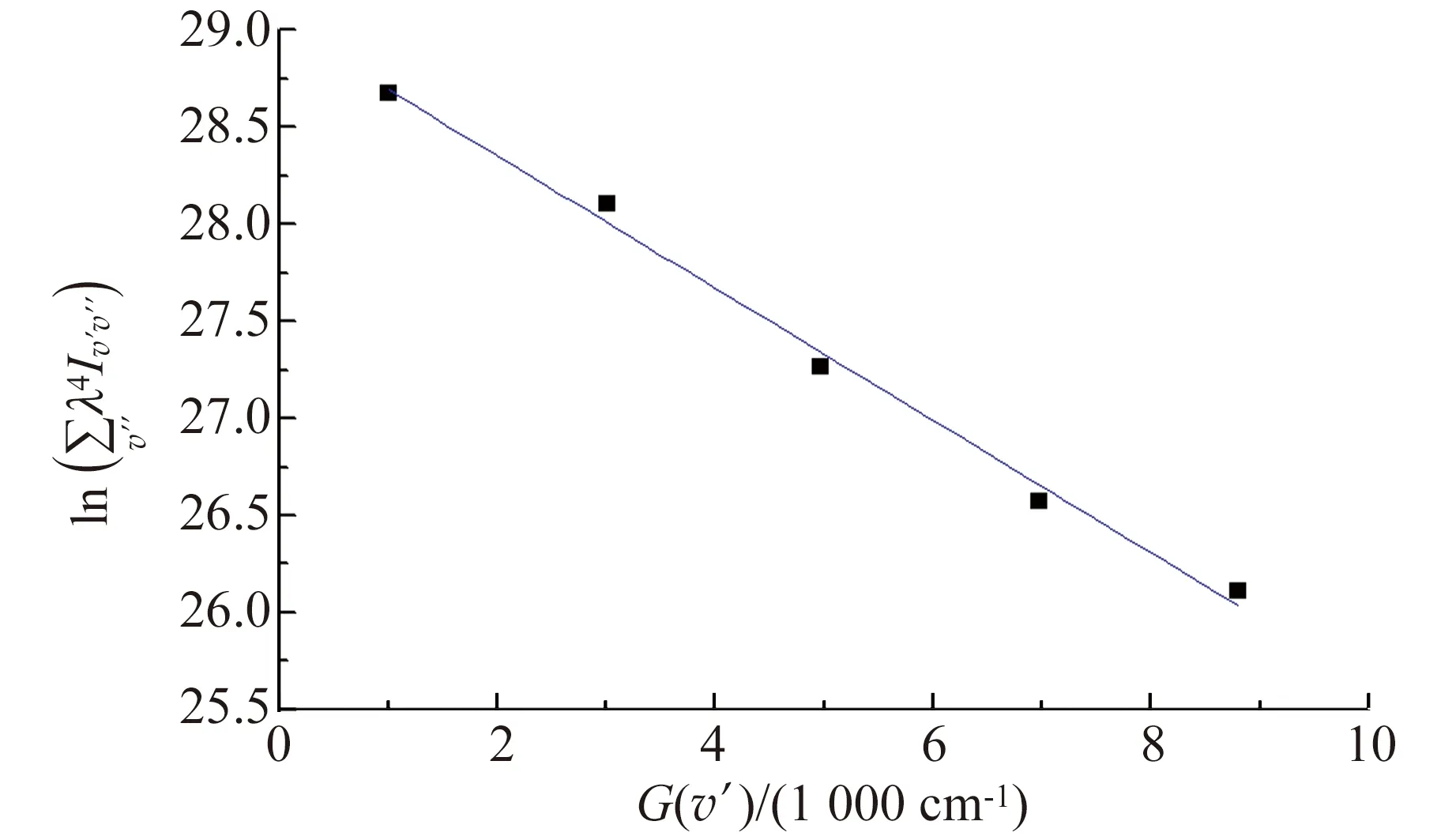
(b)玻璃管中N2C3πu振动能G(v′)玻尔兹曼图图7 文献[30]中玻璃管中探测到的N2发射光谱及玻尔兹曼图
2)不能分辨振动转动谱线的振转温度
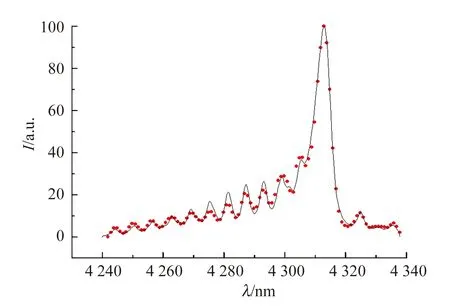
图8 文献[44]中CH(A2Δ-X2Π) (0,0)带发射光谱及LIFBASE程序模拟光谱
对于由几个振转动带的光谱叠加而成不能分辨振动转动谱线,例如CH(A2Δ-X2Π)带的发射光谱[44],如图8所示. 可以采用LIFBASE程序[43-44]通过理论模拟来获得较为精确的振动温度与转动温度.
利用上述方法,通过对在分子预解离或与其他粒子碰撞造成转动能级非热力学平衡造成[45]双温度分布或多温度分布研究,可以进一步得出内能重新分配机制[46-48],还可对燃烧过程中振动能平动能转化和分配机制进行研究[48].
3.1.4 电子温度
电子温度用来表征等离子体中粒子和电子碰撞过程的热平衡状态,也称电子激发温度. 如果处于某一能量范围的激发态上的粒子通过电子碰撞过程达到了某种局部平衡状态,那么处于第q能级的粒子数密度nq由玻尔兹曼分布给出[2,7-8]
(7)
式中,Z为配分函数,gq为统计权重,Eq是q能级的能量,Te为电子温度. 在等离子体形成的初始阶段,连续背景辐射较强,可以利用连续背景辐射来确定电子温度;在中、后期阶段,连续背景辐射较弱,而原子、分子、离子的分裂谱线很强,这时应使用这些分立谱线. 通过测量激发态粒子的光辐射强度,可以得到相应激发态的粒子数布居数之比,进而利用玻尔兹曼图解法可以得到电子温度. 电子温度与某一能量范围的电子数密度相关.
1)两谱线法
采用等离子体局部热平衡近似,可以通过测量相同原子2条谱线的相对强度来确定等离子体的电子激发温度[2,8]
(8)
式中下标1和2是分别指第一与第二条谱线.
两谱线法可用于同一元素的2条中性原子谱线的强度比,也可用属于同一元素的2条离子谱线的强度比. 在选择发射谱线计算电子温度时,还需满足E2-E1>kTe. 为测量电子激发温度,选用相距较近的Ar 763.51 nm和772.42 nm光谱线对电子温度进行分析.
2)玻尔兹曼斜率法
如果有足够多的谱线,其激发能及跃迁概率等数值为已知,则当测得它们的强度后,可由绘出曲线,如图9所示. 式中,C为常数,Ei为能级,单位eV. 温度Texc可由直线斜率求得.
(9)
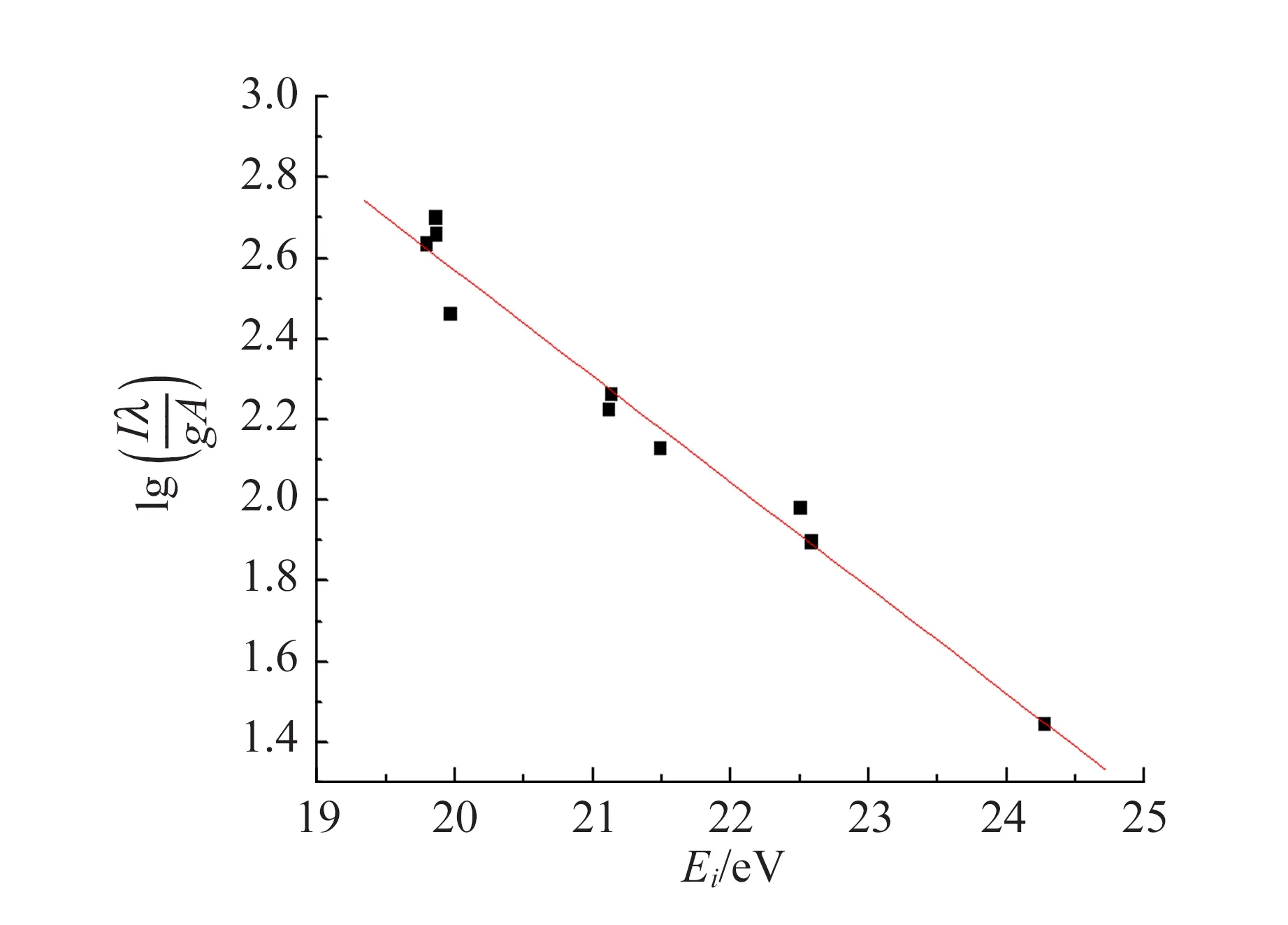
图9 文献[8]喷束中氩气放电发射光谱的玻尔兹曼曲线
使用玻尔兹曼斜率法时应注意的问题很多,如所选谱线的跃迁概率应有可靠的值,谱线应无自吸收的影响,而且谱线组的激发能差值应尽可能大,所选谱线的强度随等离子体温度的变化应该很灵敏等. 玻尔兹曼斜率法的优点:一是应用了多条谱线的信息,因此测温精度较高;二是此法还可用来验证哪些点(即哪些谱线)处于局域热力学平衡.
利用电子温度,可以监控等离子体喷枪特性、激光焊接过程、材料加工和照明形成等过程[49-50].
3)连续光谱求电子温度
在等离子体中,韧致辐射与复合辐射的相对贡献与等离子体温度密切相关,各种辐射和吸收机制共同作用达到平衡. 通过等离子体光谱的连续光谱,借助文献[51-52]公式作计算机模拟可得电子温度. 因此,此法应用到激光等离子体的电子温度、电子密度以及其随时间的演化机制研究[52-53].
3.1.5 电离温度
如果把玻尔兹曼分布应用到连续状态,就是相当于电离的情况. 粒子的分布用沙哈方程描述,与这个电离自由度相联系的温度定义为电离温度. 一次电离的沙哈方程形式为[7]
(10)
式中ni和ne分别是一次电离原子数密度和电子数密度,nα为中性原子数密度,Z1和Z分别为一次电离离子的配分函数和中性原子的配分函数,Ei为电离能,Te是电子温度,Ti是电离温度.
3.2 电子密度
为了对某种等离子体系作出有意义的理论模型,就必须很好地了解气体动力学截面、带电粒子与不带电粒子的碰撞截面、不同粒子的密度和温度等数据.在上述参量中,头等重要的是电子密度ne的数值及其随时间的变化,因为许多动力学反应速率直接或间接地依赖于电子密度[54].
3.2.1 根据半峰宽计算电子密度
当等离子体的温度比较低,电子密度在1020~1024m-3范围内,谱线的线型又是洛伦兹线型时,谱线展宽主要机制是发生辐射跃迁的原子受到德拜球内离子电场作用产生(准静态近似)的斯塔克能级分裂. 一般来说中性粒子引起的碰撞展宽和共振展宽可以忽略, 最终的谱线轮廓由斯塔克效应和多普勒轮廓决定. 当电离度不小于1%时, 由带电粒子的长程库仑力作用所决定的斯塔克效应占优势. 对于氢原子,斯塔克效应是线性展宽,它的谱线展宽与电子密度有关,这时谱线轮廓的半峰宽Δλ1/2与电子密度关系为
(11)
式中,Δλ1/2是归一化轮廓的半峰值宽度,α1/2其数据可查文献[54],例如Hβ的α1/2=0.087,ne的单位为m-3. 对于其他非类氢原子,斯塔克效应为非线性展宽,但近来一些文献也对类氢原子的谱线展宽测量电子密度进行探讨,如Al Ⅱ 281 nm谱线和Hα谱线的斯塔克加宽测得结果近似很好;文献[55-56]利用近似公式Δλ1/2=αne,得到Ar 415. 86 nm谱线,α=2.30×10-18nm/cm3;ArⅠ 430. 01 nm谱线,α=2.27×10-18nm/cm3. 文献[57]讨论了考虑电子温度影响时,利用弧室内和弧室出口等离子体射流的ArⅠ430 nm谱线,根据经验公式
lnne=58.241+0.992 ln Δλ1/2-0.414 lnTe
(12)
计算等离子体射流的电子密度. 根据式(12)讨论了在氩等离子体射流方向上, 存在着电子温度和电子密度的梯度分布.
对于除氢元素之外的其他元素的发射谱线,Griem 以列表的形式分别给出了中性原子(He Ⅰ~ Ca Ⅰ和Cs Ⅰ)和一价离子谱线(Li Ⅱ~ Ca Ⅱ)的斯塔克加宽和频移参量[54],利用他们的计算数据和实验结果对照,就能估算等离子体中的电子浓度.
利用斯塔克效应进行诊断的一个优点是,由于它是仅与电子密度有关的效应,与温度关系极微,即与等离子体是否达到热平衡关系不大,因而无论是瞬变等离子体还是准稳态等离子体,都可以应用斯塔克效应进行诊断.
3.2.2 根据光谱上可分辨的谱线极限估计电子浓度
等离子体中,由于电荷场的相互作用,原子和原子性离子的辐射谱线的半宽度,随着光谱项中的主量子数增加而增大,以至使相邻谱级间隔减小,甚至重叠. 随着电子浓度增大,这种效应将扩展到较小主量子数的光谱项,即当电子浓度增大时,可分辨谱线序列的极限向长波长偏移. 因此可分辨谱线的极限与等离子体中的电子浓度是有关的. 如图10所示,H原子光谱中可测到λ=383.498 nm原子谱线,对应nmax=9.
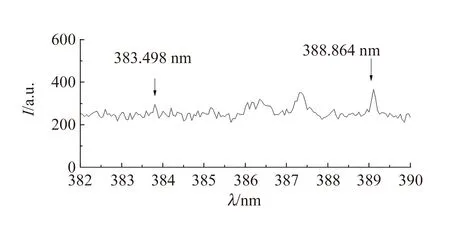
图10 文献[41]中等离子体中氢原子谱线
经计算,得出等离子体中电子浓度ne与可分辨的最后一根巴末耳谱线的主量子数nmax之间关系为[8,58]
lgne=23.94-7.5lgnmax-
(13)
(14)
其中,ND和λD分别是德拜屏蔽球内的电子数目和德拜屏蔽球半径,Zp是辐射粒子的电荷数,中性粒子Zp=0,单荷正离子Zp=1.Ze是辐射粒子的核电荷数数目,Ze(H)=1,Ze(He)=2. 只要测出可分辨的那个主量子数nmax,知道Zp,Ze和Te后就可利用式(13)~(14)算出电子浓度ne. 使用式(13)~(14)测定电子密度,其误差几乎等于一倍.原因在于:“最后可分辨”谱线并不能严格确定.不过,这项技术还是有用的,得出的公式也将会适用于所有的原子,而不仅是类氢原子.
4 结束语
发射光谱是一种时空分辨性能良好的无干扰诊断技术. 它不仅能诊断出激发态物种,而且通过光谱解析还能获得等离子体参量的诸多信息,但以前的理论一般都是建立在平衡等离子体条件下的,因此发展出对于非平衡等离子体的光谱进行准确解析的理论非常具有必要性和重要性,因为工业大规模使用的一般都是非平衡等离子体[59-63].
冷等离子体广阔的应用前景,必将推动对其内部物理化学反应机理的深入了解,这就对等离子体物种及参量的精确实验诊断提出了更高的要求. 一方面,应该不断改进现有的诊断手段和探索新的实验方法,另一方面,由于一种诊断手段通常只能探测某一种物种或参量,所以将几种诊断手段联用[32,64],并充分发挥各自的优点,将有助于准确、全面地诊断等离子体的各种物种和参量.

