动态法测杨氏模量实验中的双共振峰现象

洪子昕，郭无筝，白在桥

(北京师范大学 物理学系，北京 100875)

动态法测杨氏模量实验[1-8]是大学物理课程中基础的教学内容. 该实验测量样品的共振频率而非微小形变，具有操作简单、精确度高的优点. 但在教学中也发现该实验存在一些问题. 比如实验用示波器观察拾振器输出波形，并根据其振幅达到极大值判断共振频率. 在共振峰顶端，振幅改变不明显，导致共振频率测量精度不够高. 此外，在描频率过程中，偶尔有学生发现拾振器输出振幅出现勤率次极大值.

本文利用LabVIEW搭建自动测试系统，测量杆共振曲线的全貌和细节，从而验证双共振峰的存在性，并研究它对实验的影响.

1 理论背景

1.1 双共振峰模型

根据2009年开始实施的《金属材料弹性模量和泊松比试验方法》的国家标准[9]，动态法测杨氏模量的实验装置主体部分如图1所示. 测试杆用细棉线悬挂于仪器架上，棉绳上端连接激振器和拾振器(图中M和N下方). 激振器利用逆压电效应，将外界激励电信号转换为周期性的驱动力，借助细棉线作用于测试杆. 测试杆的振动通过棉线传至拾振器，拾振器利用正压电效应将拉力转换为电信号输出.

以测试杆质心为原点O，建立如图1所示的坐标系. 杆存在x和z方向的横向振动. 理想的情况下，由于杆具有旋转对称性，激励加在z方向，不会引起x方向上的振动. 但由于制备加工的因素，很难保证实际样品的力学性质具有精确的旋转对称性. 旋转对称性的破坏导致原本简并的本征振动频率劈裂成2个略不相等的本征频率，分别对应2个相互垂直的本征振动模式. 由于实验中只是随意放置杆的方向，这2个本征振动方向很可能都不与z轴垂直(在z轴方向的投影都不为零). 因此z方向的激励很可能同时激发出这2个本征振动，从而在扫描频率时看到2个很接近的共振峰.

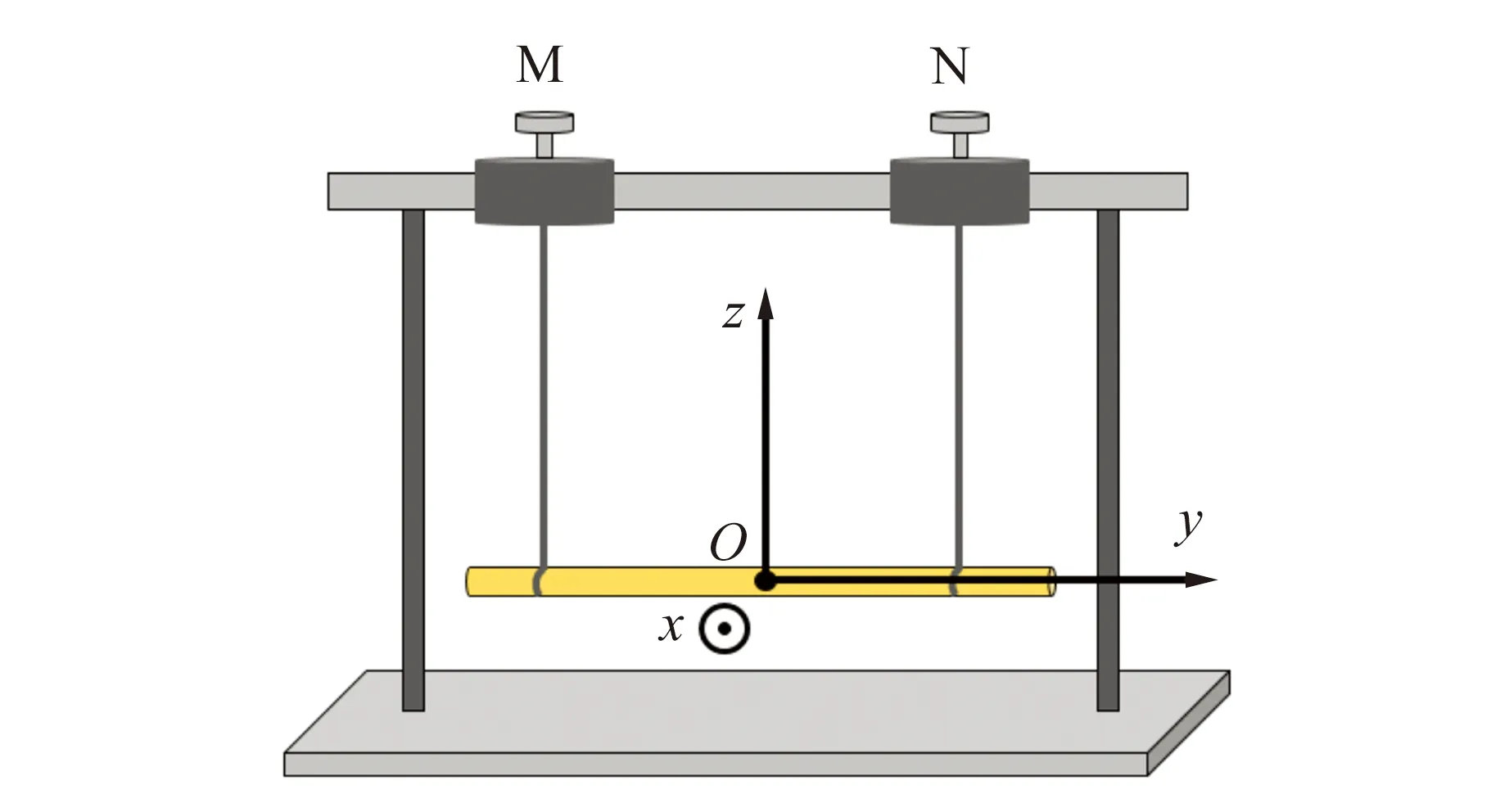
图1 实验装置主体部分示意图

假设系统处于线性响应区间，根据线性系统的一般理论，如果激振器发出正弦波形式的驱动信号

uin(t)=A0sin (ωt+θ0),

(1)

当杆振动达到稳态时，拾振器接收的响应信号一

定也是同频率的正弦信号

uout(t)=A1sin (ωt+θ1).

(2)

而且它们的幅度比A1/A0和相位差Δθ=θ1-θ0都只是频率的函数，分别称为系统的幅频特性和相频特性. 实际上把二者合并成复数的频率响应曲线要更方便处理：

(3)

在线性电路中，H(ω)可用相量法计算. 比如对RLC串联电路，若用电阻上的电压作为响应信号，则

(4)

(5)

其中Δ=R/L=ω0/Q为共振峰的宽度，Q为振子的品质因数. 一般而言，H(ω)在复平面上的每个极点都可以解释为1个共振，极点的实部对应共振频率，虚部则等于共振峰的半宽度.

根据叠加原理(并用频率代替角频率)，假设测试杆的频率响应曲线在共振频率附近可表示为包含5个复参量的函数形式

(6)

其中，f1和f2为频率响应函数在复平面上的极点，对应2个本征振动模式，c1和c2的模长与幅角分别表示这2个振动模式的响应强度与相位延迟. 在拟合实测曲线时，发现引入常数b可以显著提高拟合效果. 该常数可以理解为通过测试架直接传到拾振器的信号，或者，如果考虑位移共振，也会引入常数项.

1.2 悬挂点位置对频率的影响

计算杨氏模量需要杆的固有频率. 除非悬挂点在波节处，否则悬线的影响会导致共振频率偏离固有频率. 如果将悬挂点放在波节处，由于波节处振幅为零，又无法激励和探测杆的振动. 通常的做法是测量悬挂点在波节点两侧不同位置的共振频率，然后依照经验模型内插得到杆的固有频率[1-2]. 教学中常采用多项式模型拟合数据，这种方法虽然合理可行，但存在一定的任意性(比如多项式的阶数).

文献[6]对悬挂点对共振频率的影响做过理论分析. 假设悬线的劲度系数为k，利用微扰方法得到，当悬挂点对称地位于y和-y处时，共振频率ω(y)与固有频率ω0满足

(7)

其中G(y)为基频振动的本征函数,

(8)

式中，L为杆长，cosxcoshx=1的最小正根x1≈4.730 04，M为杆在基频振动时的广义质量,

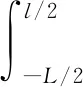
(9)

式中ρ为杆的线密度. (7)式右边第二项为修正项，数值上远小于第一项，因此有

(10)

如果(10)式成立，就可以用ω(y)与G2(y)做直线拟合，所得截距就是固有频率ω0. 从教学上考虑，这种线性拟合要比纯经验的多项式拟合更有物理意义. 本文将用测量结果检验这个方法的有效性. 需要说明的是，在推导(7)式时假设振动只发生在z方向，并没有考虑杆的各向异性. 如果测量结果与(10)式不完全相符，应全面地分析应该考虑2个本征模式与悬线的相互作用[10].

2 实验装置与方法

实验是在杭州大华生产的DHY-2 动态法杨氏模量测定仪基础完成的，主要器材包括测试金属杆、支架、激振器、拾振器和信号放大器. 其他器材包括信号发生器、数据采集卡(NI-myDAQ)和装有LabVIEW软件的计算机，其中信号发生器有USB-device接口，可以用LabVIEW控制. 使用LabVIEW软件编程控制信号发生器的输出，用于激励杆的振动，然后通过数据采集卡获得拾振器输出(经过仪器放大后)的响应信号.

测量程序自动扫描激发频率，在每个频率点采集激励信号与响应信号，计算振幅比与相位差，并把结果保存在文件中. 程序可以设置扫频的范围、步长和方向. 为了观察共振曲线的细节，还可以在一定区间内采用更细的扫频步长. 为了确保测量时振动已经达到稳态，程序在激励信号频率改变1 s之后连续测量20次信号(每次采集时间50 ms). 测量20次响应信号的振幅，计算幅值与1到20序号之间的线性相关系数r. 如果r2接近1，说明响应振幅还在稳定地增加或减小. 把r2小于某阈值(实验中取0.65)当作振动达到稳定的判据. 如果判据满足，就将这20次测量结果取平均作为测量结果，然后将信号源频率调至下一个频率点，继续测量. 如果r2大于阈值(这种情况一般只出现在共振峰附近)，则保持频率不变，重复上面的测量-判断过程，直至满足稳定判据. 程序最快2 s就可以完成1个频率点的测量，完成1条频率特性曲线的测量需要8～10 min.

实测的频率特性曲线都包含2个共振峰. 图2和图3给出了2个典型的频率特性曲线. 图2中的2个共振峰重叠部分很小，此时把幅频特性曲线极大值的位置当作共振频率，不会引入可观的误差. 图3是小而窄的共振峰和大而宽的共振峰的叠加. 2个峰的中心很接近，但相位几乎相反. 叠加的效果是在大共振峰的中心附近出现向下的凹陷. 此时把幅频特性曲线的2个极大值点位置当作共振频率显然不合适.

(a)幅频特性

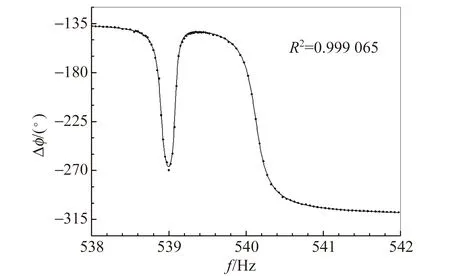
(b)相频特性图2 铜杆的幅频特性和相频特性曲线

编写拟合程序，采用非线性函数拟合常用的Levenberg-Marquardt(L-M)算法按照式(6)拟合实测频率响应曲线，得到2个共振频率及其宽度. 需要说明的是，一般的L-M算法(包括LabVIEW自带的)都只针对实参量的情况. 对于复参量情况，需要将梯度的转置变成共轭转置. 拟合效果的优劣常用决定系数来衡量，其定义为

(11)

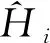
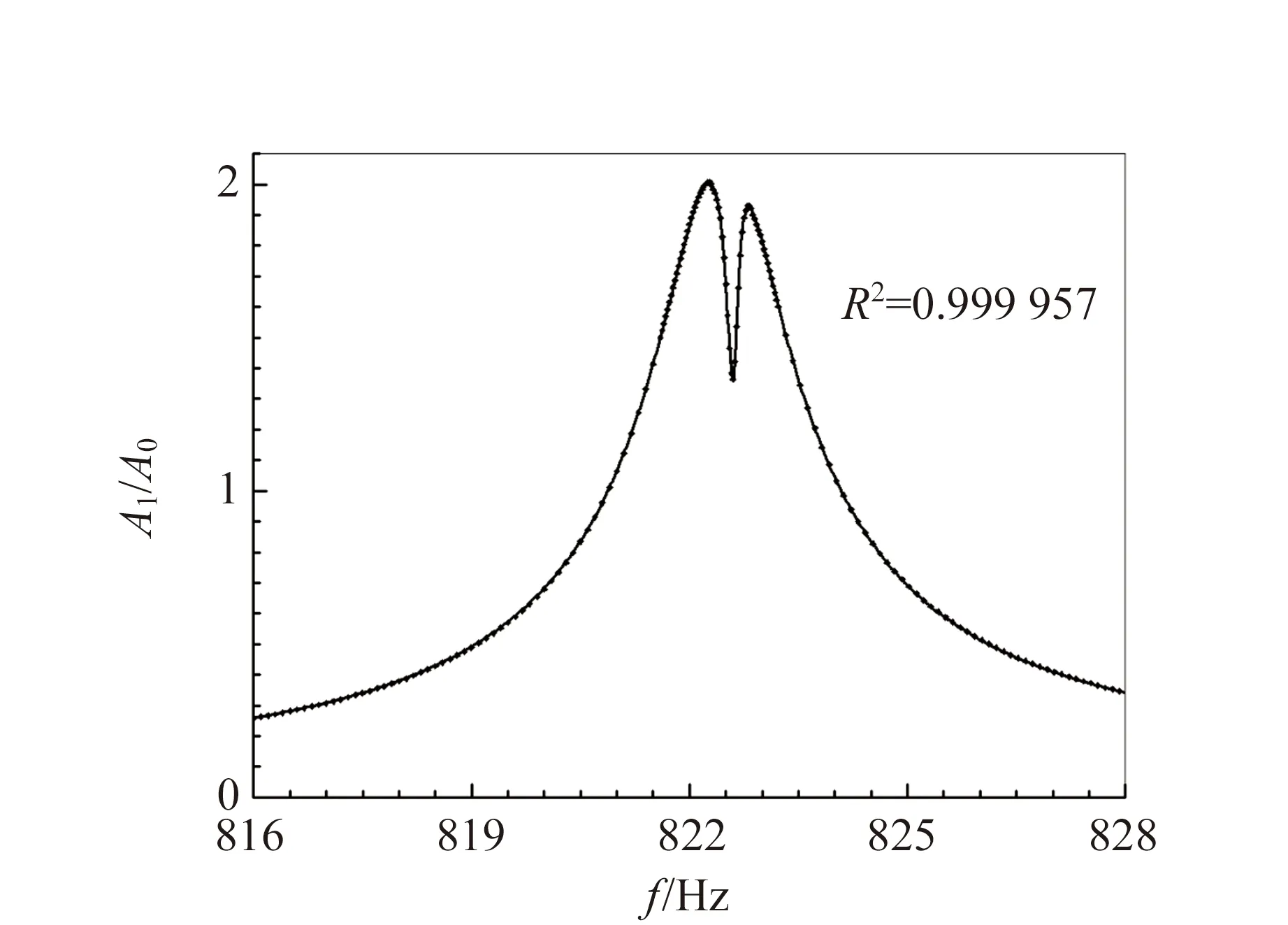
(a)幅频特性

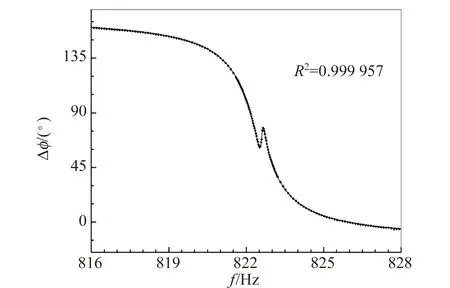
(b)相频特性图3 不锈钢杆的幅频特性和相频特性曲线

为检验频率测量的可重复性，连续多次测量了向上扫频和向下扫频的频率响应曲线，发现拟合共振频率相差都在0.01 Hz以内. 此外，从1 V到3 V改变激发信号的峰峰值，对结果的影响也没有超过这个限度.

3 实验结果

使用相同的测试架(包括悬线)，改变悬挂点位置，测量了黄铜和不锈钢杆的共振曲线并拟合得到2个共振频率及其宽度. 为了减小杆各向异性的影响，在测量过程中尽量保持杆悬挂的角度不变. 测量结果见表1和表2. 在2个共振频率中，虚部较小的记作f1，虚部较大的记作f2. 为方便参考，表中还给出了对应悬挂位置的G2(y)(取L=180 mm).

图4画出了黄铜杆共振频率与G2(y)的关系. 可以看出f1的实部和虚部变化都很小，它们与G2(y)都没有明显的相关，但f2的实部和虚部都与G2(y)显著地线性相关. 将f2的实部线性外推到G2(y)=0，所得杆的固有频率为539.831 Hz，与f1的实部相差在1 Hz左右. 这个差异体现了杆本身的各向异性. 共振频率的虚部大小体现了振动能量耗散的快慢.f1的虚部与G2(y)关系不大，表明它对应的振动受到悬线的阻尼比较小. 而f2的虚部随G2(y)线性增大，表明对应的振动受悬线的阻尼比较大.

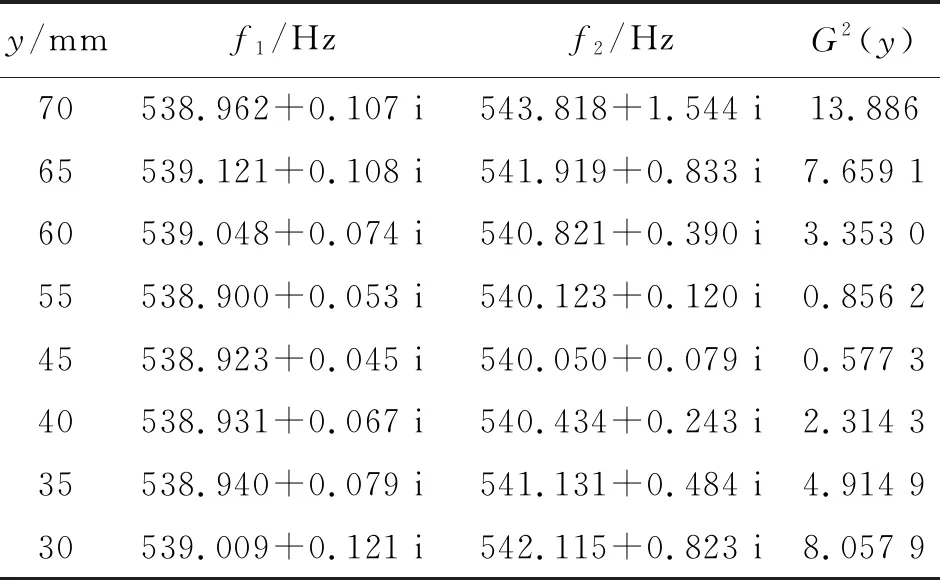
表1 黄铜杆的共振频率

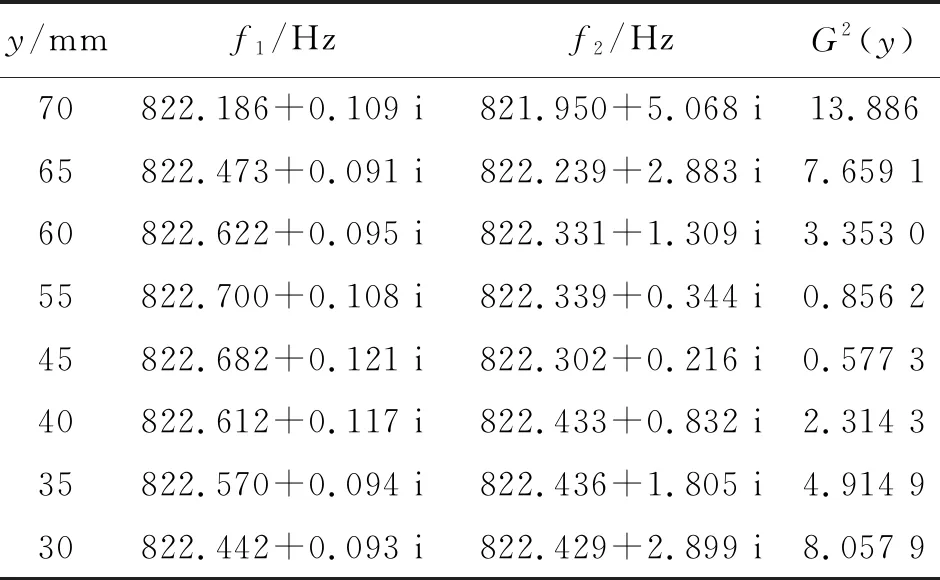
表2 不锈钢杆的共振频率

(a)频率的实部

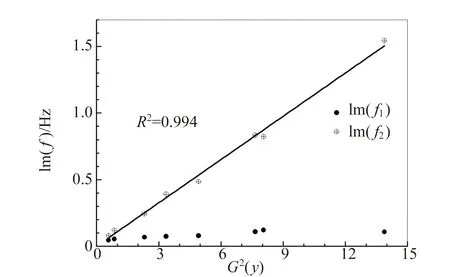
(b)频率的虚部图4 黄铜杆的共振频率与悬挂点G2(y)的关系

不锈钢杆的结果则有些令人意外(见图5). 一方面这里f1的虚部和f2的实部与G2(y)的相关不显著，而f1的实部以及f2的虚部与G2(y)线性相关度比较高. 另一方面，f1的实部与G2(y)呈负相关. 式(10)中的系数为悬线的劲度系数，不可能为负. 因此猜想悬线不仅会引入额外的弹性，还可能引入额外的质量. 事实上，悬线上存在弹性波，其力学性质应该与频率有关. 为了检验悬线在对共振频率的影响程度，换了更细、更硬的悬线重新测量了不锈钢杆的共振频率，结果见表3和图6.

(a)

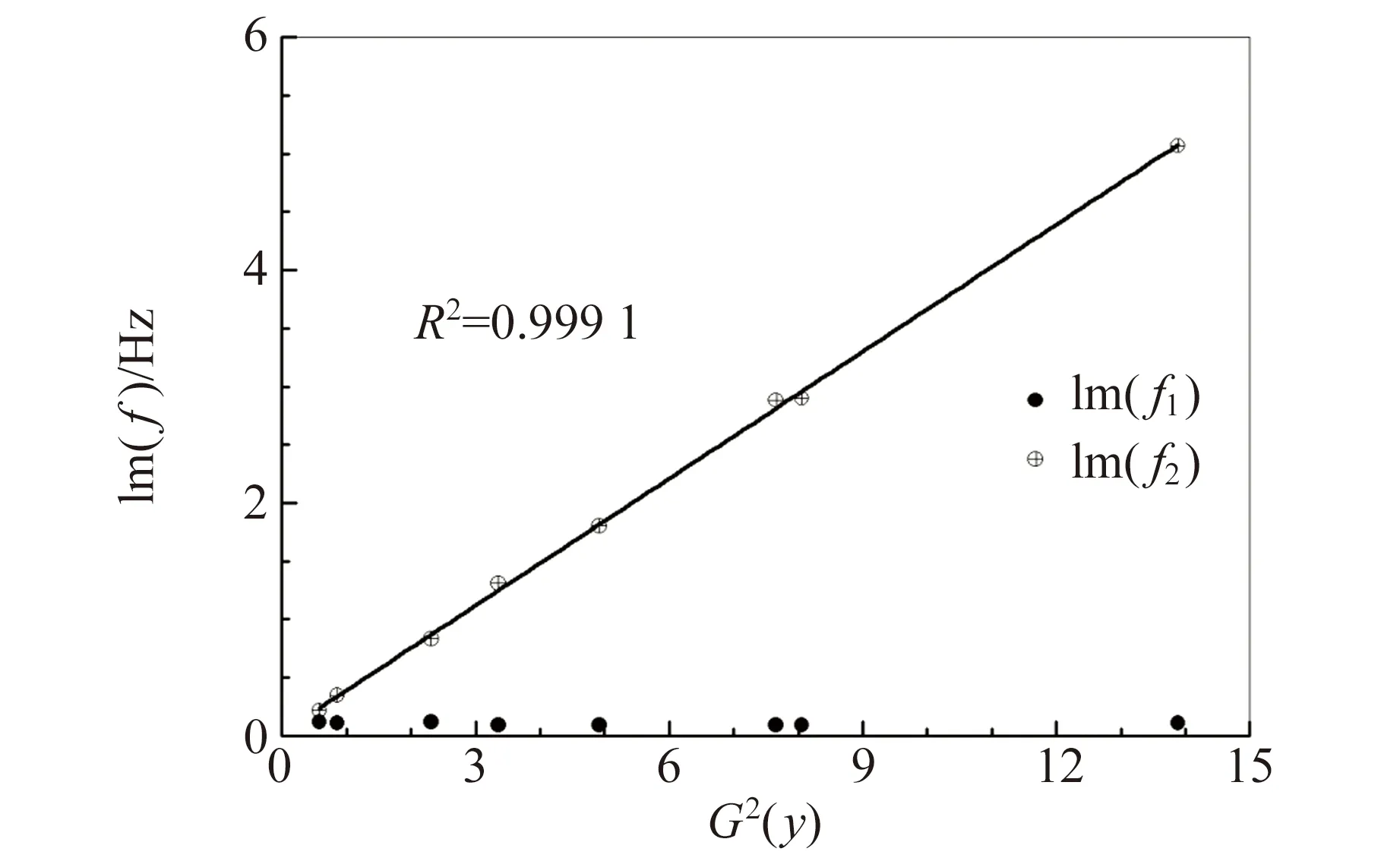
(b)图5 不锈钢杆的共振频率与悬挂点G2(y)的关系

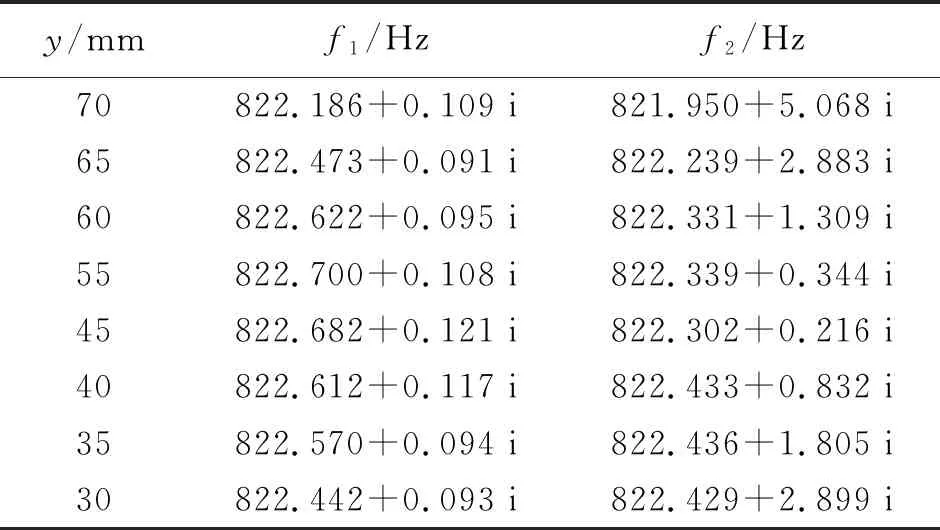
y/mmf1/Hzf2/Hz70822.186+0.109 i821.950+5.068 i65822.473+0.091 i822.239+2.883 i60822.622+0.095 i822.331+1.309 i55822.700+0.108 i822.339+0.344 i45822.682+0.121 i822.302+0.216 i40822.612+0.117 i822.433+0.832 i35822.570+0.094 i822.436+1.805 i30822.442+0.093 i822.429+2.899 i

(a)

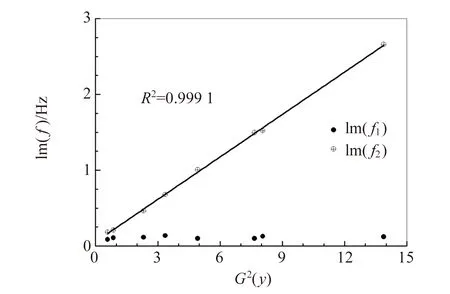
(b)图6 更换悬线后不锈钢杆的共振频率与悬挂点G2(y)的关系

新悬线的结果看起来又“正常”了：f1与G(y)2关系不大，f2的实部与虚部都与G(y)2线性正相关. 不过图5(a)中线性外推波节点f1的实部为822.728 Hz，而表3中最靠近波节点的2个f1的实部的平均值为822.691 Hz，二者相差并不大. 按照相同的做法，从表2得到波节点f2的实部为822.321 Hz，从图6(a)线性外推得波节点f2的实部为822.300 Hz，二者相差也不大. 这说明虽然悬线对杆的共振频率影响比较大，但用直线外推或者近邻点取平均，在推断固有频率时基本可以消除悬线的影响.

根据以上实验结果，提出改进的计算固有频率的方法：如果共振频率随悬挂位置变化较大，可用线性外推法计算固有频率；如果变化不明显，则用近邻点取平均计算. 用此方法求得杆的2个固有频率，并根据

(12)

计算杨氏模量，结果见表4.

表4 黄铜和不锈钢(2次)杨氏模量测量结果

4 总结与讨论

利用LabVIEW精确地测得了样品的频率响应曲线，确认了双共振峰的存在. 通过拟合双共振频率响应曲线，比较准确地确定了2个共振频率及其宽度. 通过测量不同悬挂位置以及不同悬线对共振频率的影响，发现悬线的影响不止是提供了额外的弹性，使共振频率增加. 悬线的影响还包括提供阻尼造成杆共振峰宽度增加(品质因数减小)以及提供额外的附加质量使共振频率减小. 杆的各向异性以及悬线和杆(甚至包括激振器和拾振器)耦合构成的多自由度振动系统，在实验中表现出相当丰富的现象. 基于本文的工作，对这个实验提出2条建议：

1)尽量减小样品力学性质的各向异性，否则2个固有频率相差过大会影响杨氏模量测量的准确度. 为此应避免在样品上刻线(必要时可用喷涂代替)，对样品退火处理也可以减小其各向异性.

2)在外推杆的固有频率时，可以用共振频率与G(y)2作图. 如果线性度较好，可以把拟合直线的截距当作固有频率(笔者用此方法分析了文献[1]的数据，结果为R2=0.988). 如果共振频率变化很小，可以取最靠近节点的2个测量的平均值作为固有频率. 如果线性度不高但共振频率本身变化比较大，则很可能测量数据有问题.

致谢:感谢北京师范大学研究生吕博文在实验过程中给予的帮助.