解题教学要重视“破题”与反思回顾——以两则解题教学的片段为例

☉江苏省海安市城南实验中学 邓厚波

解题教学、习题讲评几乎在每节数学课中都有体现，但是不同的数学教师对解题教学的认识和理解有很大的不同，特别是一些未经充分准备的解题教学，往往就题讲题，没有触及问题本质，也就是史宁中教授所指出的：只知道在讲题，但没有“破题”.本文结合最近听两节随堂课中记录的讲题片段，跟进评析并提出教学建议，供研讨.

一、两则解题教学的片段及教学建议

教学案例（一）“含参”二次函数综合题讲评

说明：这是一份中考模考卷的第26题第（2）问，据讲评老师说阅卷时发现很多学生没做出来，班上只有3名学生用了不同的思路解题，上课前布置了这3名学生先讲解此题.

习题1：已知二次函数y=-x2+bx-c的图像与x轴的交点坐标为（m-2，0）和（2m+1，0）.

（2）若y=1时，自变量x有唯一的值，求二次函数的解析式.

生1：题目中提到二次函数的图像与x轴的交点坐标为（m-2，0）和（2m+1，0），所以可以先求出对称轴：x=，结合y=1，代入二次函数表达式中，解关于m的方程可得解.

生3：由图像与x轴的交点坐标为（m-2，0）和（2m+1，0），可以设二次函数的“交点式”为：y=-（x-m+2）（x-2m-1），再把顶点坐标代入计算.

师：这三名同学的解题思路各不相同，他们在解题时都注意到了什么？

师：题目中什么条件可以帮助你得到顶点的坐标？

生1：由（m-2，0）和（2m+1，0）可以得到顶点的横坐标为

生2：y=1时，自变量x有唯一的值，说明y=1是顶点的纵坐标.

师：生5（成绩中上），你在解题时看出顶点的坐标了吗？

生5：看出来了.

师：后面为什么没有做出来呢？

生5：后面不知道怎么做.

师：这道题的最终目标是什么？

生5：求这个二次函数的解析式.

师：这就是你应该接着思考的方向，题目中已有解析式y=-x2+bx-c，可以将b、c用m来表示，比如他们3人的做法，可以将解析式重新设为顶点式或交点式，当我们在解题中失去方向时，不妨看看我们的目标，它也许能为我们引路，当我们沿着方向找不到路时，不妨看看条件，它也许就是解题走向成功的基石.

简评：虽然上述教学对话让不少学生似乎理解了这道题的解答，但是我们觉得这类问题的教学关键没有讲到位.那么什么是这道习题的关键步骤？ 除了在上述对话中教师反复提及的顶点坐标我们认为处理这类“含参”二次函数的另一个关键就是“消参”，就像二元一次方程组的求解一样，需要引导学生重视消去多个参数，如不看后续设问，就应该能够把二次函数解析式中的b、c用含m的式子表示出来，从而再借助对最值或顶点的分析就能实现问题解决.教学中可以适时出示一些提示性、铺垫式问题：

问题1：用含m的式子分别表示b、c；

问题2：画该二次函数的图像（抛物线，草图），并用含m的式子表示顶点的坐标.

教学组织：教学过程中让学生围绕这两个问题充分讨论、交流、展示，可以实现铺垫问题的教学价值，促进学生想清、想透问题求解的关键.

教学案例（二）旋转后探究定点与动点的最小距离

习题2：在平面直角坐标系xOy中，点O（0，0）、A（2，0）、.将△OAB绕点O顺时针旋转α（0°＜α＜360°）得到△OA′B′，（其中点A旋转到点A′的位置）设直线AA′与直线BB′相交于点P，则线段CP长的最小值为（）.

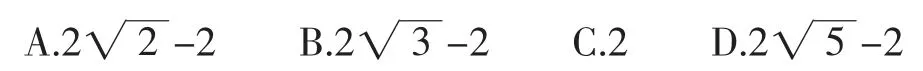
师：由题目我们可以知道，C是定点（-2，0），而P是动点，所以要求线段CP长的最小值，我们需要知道什么呢？

生1：点P的运动轨迹.

师：非常好，那点P的运动轨迹是什么呢？请同学们根据题目中的已知条件先自行画出图形来思考.

（学生自己画图，教师巡视，发现了几种不同的画法，挑选其中的图1摘记如下，有几个学生因为画图不精准，比如旋转后△OA′B′的形状与大小发生变化，影响了思路探究的方向，教师提醒了学生作图要准确）

师：这种图形对应的是α在什么范围内的情形？

生2：0°＜α＜90°.

师：还有同学画的是旋转角度在90°＜α＜180°、180°＜α＜270°或者270°＜α＜360°的吧，你们把图形检查一下：是否精准构图？通过这些有代表性的图形，你能发现点P的运动轨迹吗？如何说明呢？

（学生眉头紧锁，感觉还是无从下手）

师：换个问题，你能求出∠APB的度数吗？请同学们对照各自所画的图形求解.

（学生思考，在练习本上书写过程，教师在巡视过程中发现一些成功的解法，安排相应学生上台讲解）

生3：由旋转过程我们可以知道，OA=OA′，OB=OB′，∠AOA′=∠BOB′=α，所以可以得到△AOA′～△BOB′，所以∠OAA′=∠OBB′.又∠OAA′+∠OAP=180°（平角的定义），所以∠OBB′+∠OAP=180°，所以在四边形OAPB中，由四边形内角和为360°，可以得到∠AOB+∠APB=180°，所以∠APB=90°.

师：嗯，好，说得非常详细.得到∠APB=90°.那么其他不同旋转角度情况下是不是也能得到∠APB=90°呢？哪个同学来说明一下？

生4：同样可以得到，因为证明相似或推导等角的一些要素都没有变化，只是图形位置发生了变化.

师：你们分组再互相讲解一下证明直角的过程.

师：现在知道了始终有∠APB=90°，那你说点P的运动轨迹是什么呢？

生5：以AB为直径的圆.

生6：会！

师：那么，谁来给大家说一下？好的，你上台讲解一下.

生6：首先，我们可以知道点P运动的圆的圆心，记为点Q，其坐标为，半径为2.CP最小就是CQ-r，即

师：同学们听懂了没有？

生：（齐）懂了.

师：好的，如果我要求CP长的最大值呢？

生：（齐）CQ+r.

师：相信同学们下次再遇到这类题型应该能够解决了.

简评：这道考题突破的关键是三角形绕原点旋转后其中一组对应边所在直线的夹角问题，从上面的教学对话来看，教师在这个方面引导学生进行了较为深入的讨论，并且在不同旋转后的图形位置进行了画图探究，教学用时较多.我们认为，从解题教学效率来看，不宜让学生画出这么多旋转之后对应的图形，这些图形的精准构图耗时费力，是一种较为盲目的试探性质的“实验画图”，通过大量“实验画图”发现规律对于考场上解决这类问题消耗的时间来说成本太高，并不是有效的应试解题指导.考虑到选择题解题的特殊性，我们可以任选一个旋转角度，以特殊角度30°、45°或90°为例，可以构造一些特殊位置，获得求解方向之后，引导学生“走向一般”进行思考、归纳并大胆猜想，如果有条件，教师课前应该制成几何画板的演示课件，以提高课堂效率.

二、进一步的思考

（一）开展较难习题讲评之前教师精心备题

从上面两则解题教学片段来看，教师在上课之前都对相关学生答题进行了批阅，教师本人也理解了学生的一些不同解法，所以安排了不同学生上台讲解，并跟进追问，看似准备得比较充分，其实精心备题还有很多可以提升之处，比如，教师要想清问题求解的关键步骤，并从学情研判出发，思考多数学生不能顺利求解的原因是什么，需要在哪些方面加强引导、教学干预，就如我们在上面提供的一些操作性建议一样，这样的“铺垫式问题”在课前充分预设了，就可以让课堂讨论、交流有一个主线，以免学生的讲题“踩着西瓜皮，滑到哪里是哪里”，造成解题教学效率的低下.

（二）解题教学后要安排解后回顾、明辨难点

从上面两个解题教学的片段来看，教师在解题教学之后，都没有引导学生反思回顾，想清辨明这些较难题的关键步骤、易错之处，这是一种教学遗憾.美国著名数学教育家波利亚在名著《怎样解题》中一再强调解后回顾的重要性，是值得我们倾听的，并将这种解后回顾与反思传递给学生，让他们也懂得解后回看问题结构、关键步骤、难点障碍点等，这样的教学环节就像从“黑暗中摸索”走向“开灯看清”一样，不可或缺.