永磁同步电机的有限时间动态面位置跟踪控制
胡成江,于金鹏,于海生,付 程
(青岛大学,青岛 266071)
0 引 言
永磁同步电动机(以下简称PMSM)相比于其他电动机结构简单、易于维护、能量转换效率高,因此,PMSM在工业控制领域中应用广泛。PMSM的矢量控制方法可以保证系统有良好的稳态响应,但是动态响应较差。考虑到PMSM的动态模型是一个非线性和强耦合的模型,目前对PMSM的控制仍然是一个热门问题。为了实现对PMSM驱动系统的高性能控制,专家学者们提出了很多非线性控制方法,如反馈线性化控制[1]、滑模变结构控制[2]、自适应控制[3,7]、反步控制[4-5]和动态面控制[6]等控制方法。
反步控制技术是非线性控制领域的一大突破,反步控制技术可以保证系统的跟踪效果,提高系统的瞬态性能,但是反步控制算法中的“计算爆炸”问题,使其不能得到广泛的应用。1997年,Swaroop D 提出了动态面控制技术[19],动态面技术与反步控制技术相结合,通过引入一个低通滤波器,解决了反步控制算法中“计算爆炸”的问题。文献[6]将动态面控制技术运用到非线性动力系统控制中,在解决系统“计算爆炸”问题的同时,使系统的跟踪误差在规定的范围内,同时闭环系统其他的所有信号被限制在一个小的邻域内。文献[18]将动态面技术运用到PMSM控制中,构造了一个自适应动态面控制器,避免了反步控制算法中的“计算爆炸”问题,但系统的跟踪误差在时间趋于无穷大时,才能达到理想的跟踪效果。
在另一个研究领域上,有限时间控制技术[12-15]具有响应更快、跟踪精度更高和抗干扰能力更强的优点,文献[20-22]研究了高阶非线性系统的有限时间控制,但只考虑了稳定性问题,然而在一些工程应用中的跟踪问题也应该得到解决。有限时间控制技术[13,22]运用到跟踪控制中可以达到更理想的效果。动态面反步控制技术可以有效地解决非线性系统的跟踪问题,但是如何在动态面反步控制的基础上,使跟踪误差能够在有限时间内达到理想的效果这一问题仍未解决。
基于上述问题,本文研究了PMSM的有限时间动态面跟踪控制技术,引入神经网络技术[8-11]来逼近系统中存在非线性未知项,通过自适应技术解决了神经网络控制算法中存在参数未知的问题,利用动态面控制解决了反步控制算法中不可避免的“计算爆炸”问题,在保留动态面自适应神经网络反步法优点的基础上,引入有限时间技术[12-15],提高了系统的收敛速度,本文的控制方法,与目前PMSM控制方法相比,主要的优点如下:
1)与文献[18]的控制技术相比,引入有限时间控制技术,提高了系统的收敛速度。
2)与文献[4]的控制技术相比,本文采用了动态面控制技术,解决了传统反步控制技术中“计算爆炸”的问题。
3)控制器只需一个自适应律,减小了在线计算时间,更适于工程应用。
1 建立PMSM数学模型
在d-q坐标下,PMSM的数学模型:
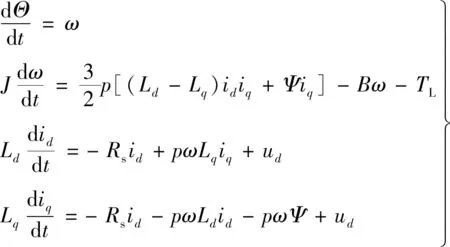
式中:Θ为转子角度;id和iq分别为d轴和q轴电流;ud和uq分别为d轴和q轴电压;Rs为定子电阻;ω为转子角速度;Ld和Lq分别为d轴和q轴电感;p为PMSM的极对数;J为转动惯量;B为摩擦系数;T为电磁转矩;TL为负载转矩;Ψ为磁链。
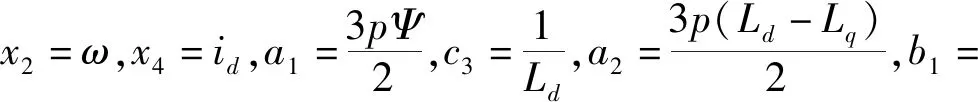
PMSM模型可以表示:

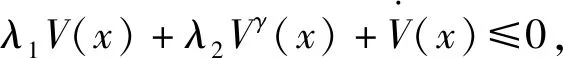
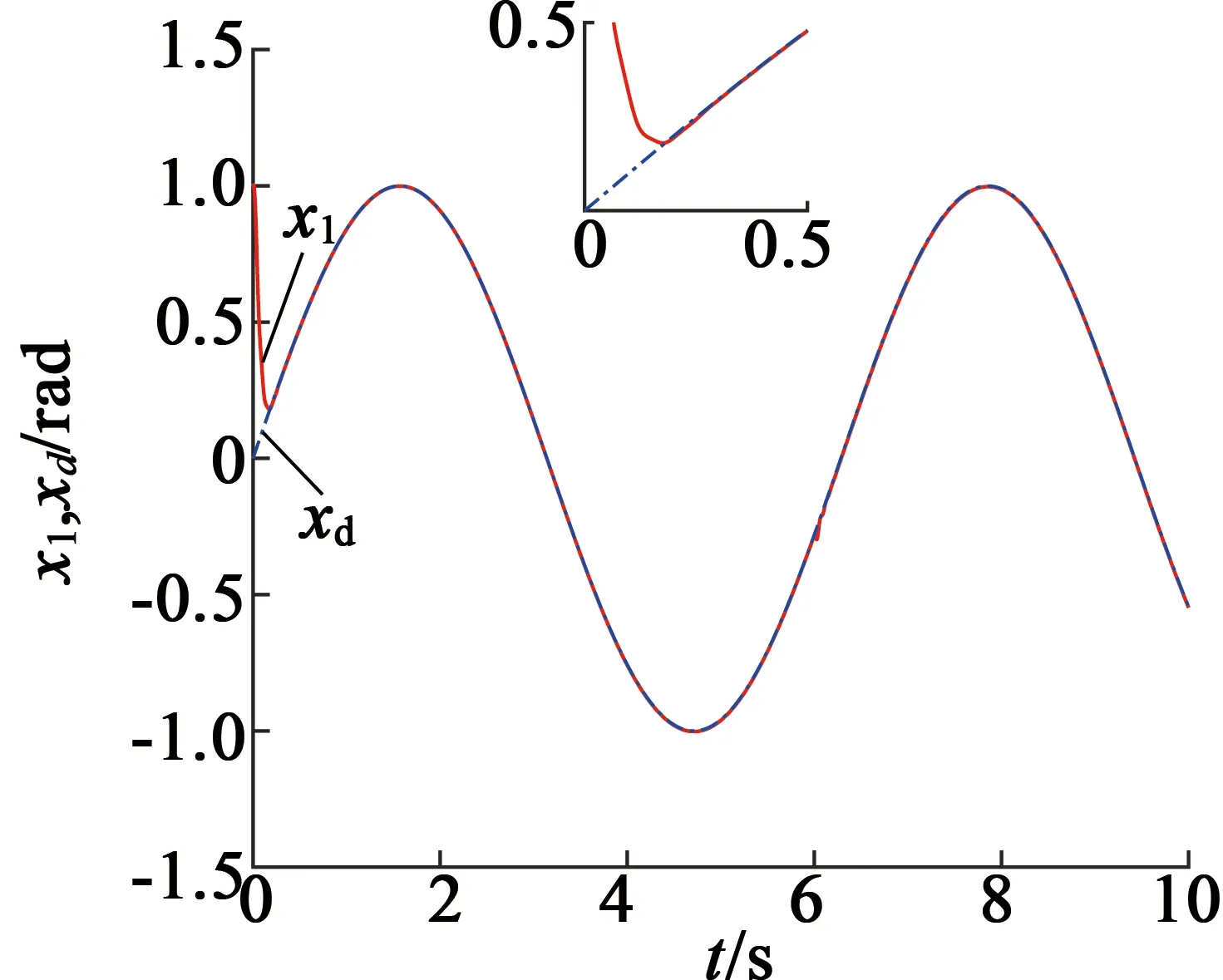
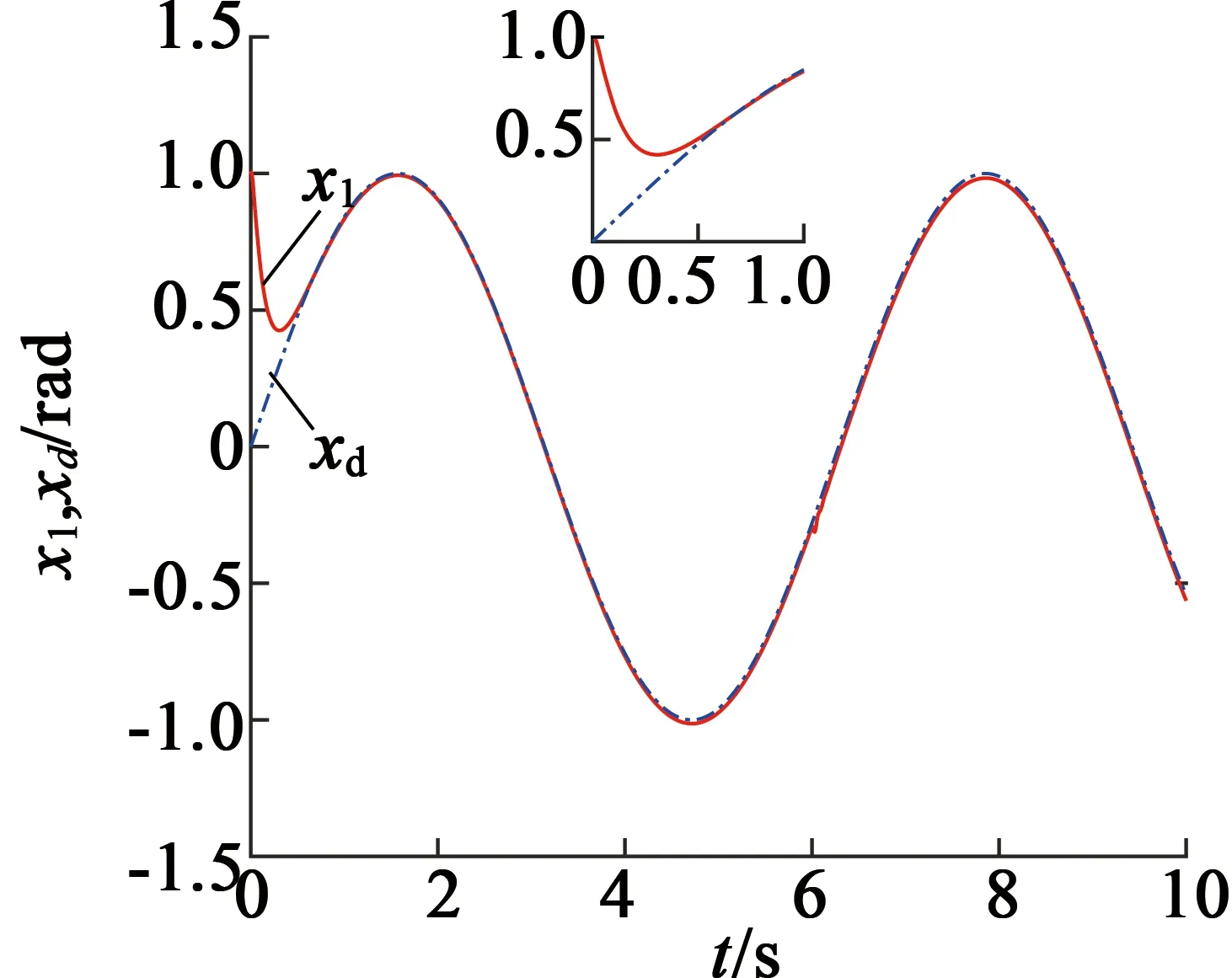
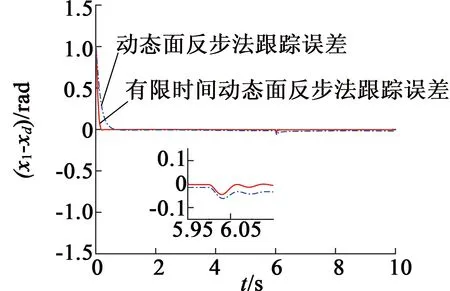
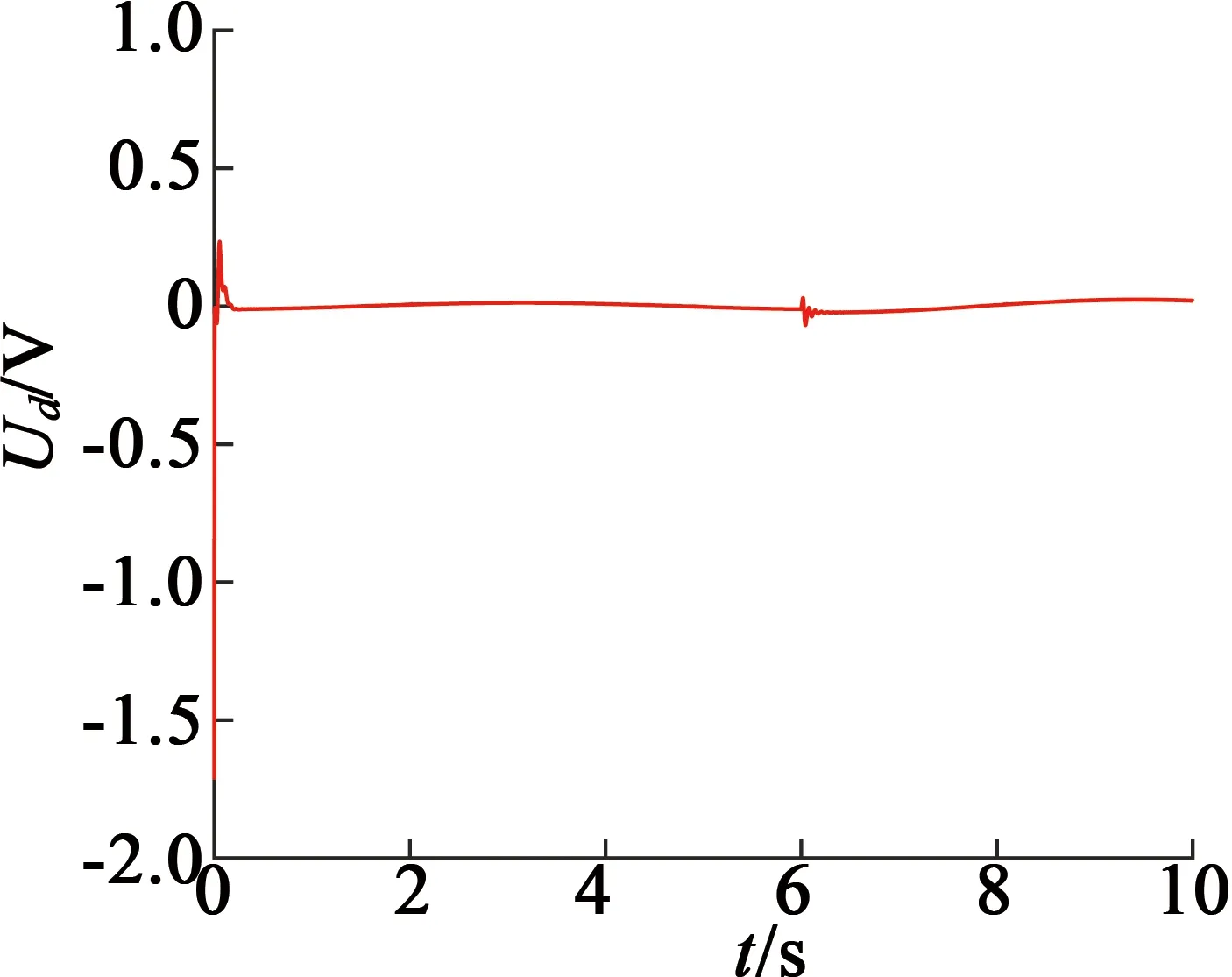
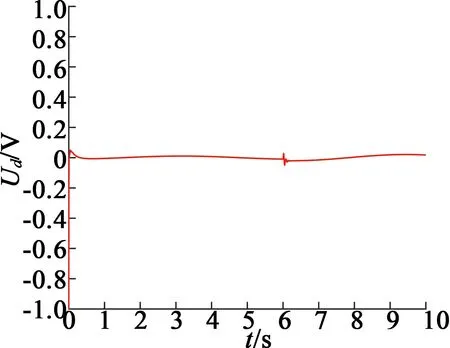
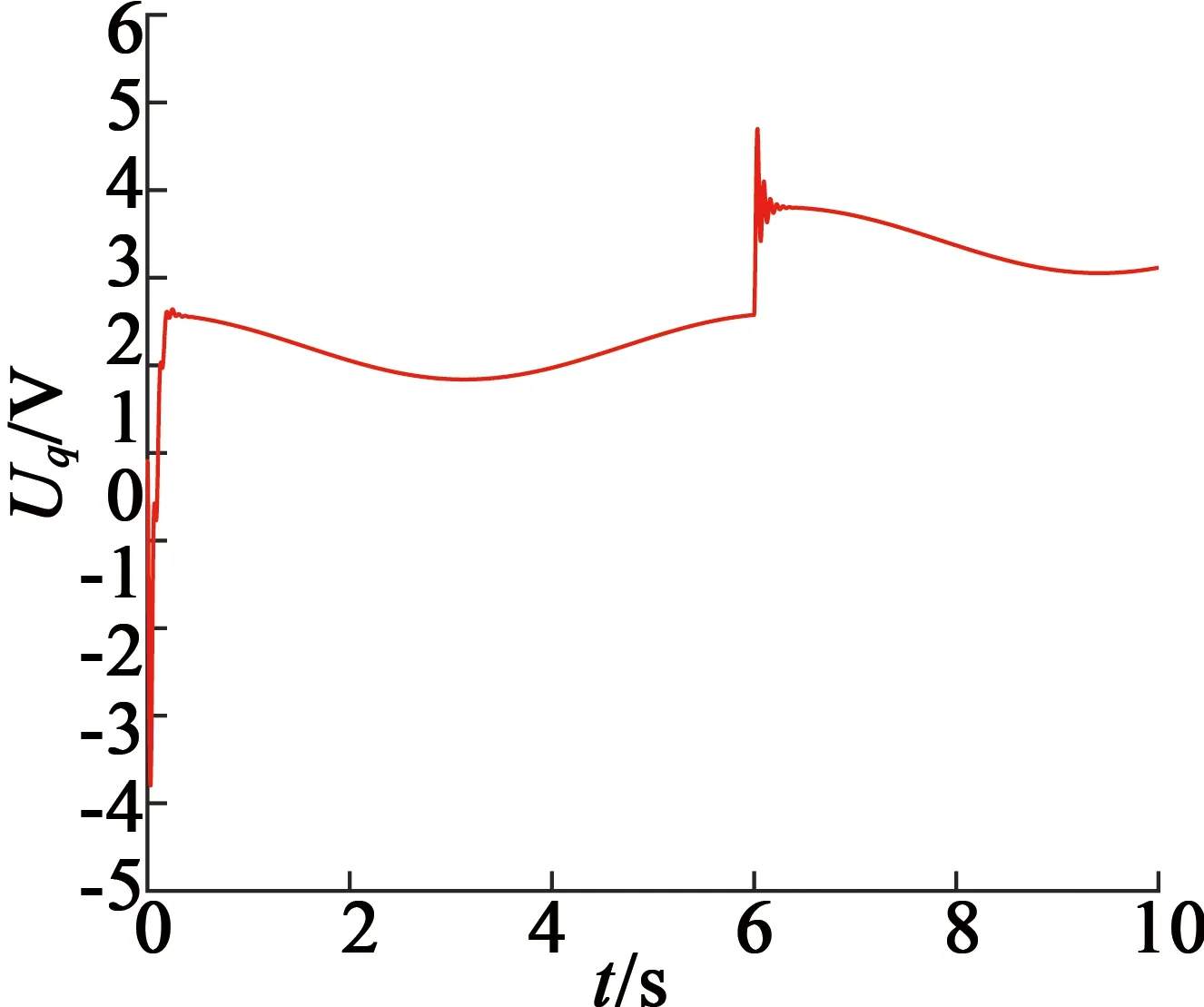
引理2[13]:任取xi∈R,i=1,2,…,n,0 式中:vi=[vi1,…,viq]T是接受域的中心;qi是高斯函数的宽度。由文献[17]可知,给定标量ε>0,选择足够大的l,RBF-NN能够在紧集Ωz⊂Rq下逼近任何连续函数:φ(z)=ΦTP(z)+δ(z),∀z∈Ωz⊂Rq,其中δ(z)为跟踪误差,跟踪误差满足|δ(z)|≤ε;Φ是为分析而定义的未知的理想权向量,Φ的取值为Φ*时,使|δ(z)|在z∈Ωz中取得最小值,其定义如下: 定义系统误差变量,其中xd为给定的期望: (1) (2) 构建虚拟控制函数: (3) 式中:k1>0,引入一个新的状态变量α1d,使α1通过一个时间常数为1的一阶滤波器: (4) 将式(1)、式(3)、式(4)代入式(2),得: (5) (6) (7) 构建虚拟控制函数: (8) (9) 将式(7)~式(9)代入式(6),得: (10) (11) (12) 设计其真实控制律uq: (13) 将式(12)和式(13)代入式(11),得: (14) z4[f4(Z4)+c3ud] (15) (16) 将式(16)代入式(15)中,得: (17) 设计其真实控制律ud: (18) 定义θ=max{‖φ2‖2,‖φ3‖2,‖φ4‖2},将式(18)代入式(17),得: (19) (20) 得到如下等式: (21) (22) 式中: D1=-α·1 D2=-α·2} (23) 取自适应率: (24) 式中:m1,r1和li(i=2,3,4)均为正数。 选择如下Lyapunov函数: (25) 式中:r1为正数。对V求导,得: (26) 将式(24)代入式(26),得: (27) 由文献[18]可知,|Di|在紧集|Ωi|上具有最大值Dim(i=1,2),|Di|≤Dim,由此可得以下不等式: (28) 式中:τ>0。由杨氏不等式得: (29) (30) (31) 将式(28)~式(31)代入式(27),得: (32) (33) (34) 由式(33)和式(34)可得: (35) 同理,可得: (36) (37) 由上式可得: (38) 由式(38)可得: (39) 在真实控制律uq和ud的作用下,PMSM控制系统在有限的时间内达到稳定状态,其位置跟踪误差在对应的时间内收敛于原点周围期望的邻域内,由此证明该方法是有效的。 为了验证本文的PMSM有限时间动态面跟踪控制技术在控制系统中的有效性,在MATLAB环境中进行仿真。PMSM的数学模型中电机及负载参数如下:J=0.003 798 kg·m2,Ld=0.003 15 H,p=3,Lq=0.00285H,B=0.001158N·m/(rad·s-1),Rs=0.68 Ω,Ψ=0.124 5 H。 控制器参数选取如下:k1=6,k2=75,k3=65,k4=430,r1=0.05,l2=l3=l4=3,m1=0.05,1=59,2=2,γ=0.818 1,s2=6,s3=15,s1=7.5,s4=114。 在PMSM零初始状态下进行仿真,给定的期望跟踪信号xd=sint,设定其负载转矩: 仿真结果如图1~图5所示。 图1为在有限时间动态面反步法控制下仿真结果,图2为在动态面反步法控制下仿真结果,由图1和图2可知,与动态面反步技术相比,有限时间技术可以提高系统的收敛速度。系统在两种方法控制下的位置跟踪误差波形对比如图3所示,引入有限时间控制技术后PMSM位置跟踪误差更小,系统的抗干扰能力更强。图4为图1控制方法下d轴电压和q轴电压的波形图,由图4可知,ud和uq的值都稳定在一定范围内。图5为动态面控制技术下d轴电压和q轴电压的波形图。 图1有限时间动态面反步法控制下x1和xd的波形 图2动态面反步法控制下x1和xd的波形 图3两种控制方法下跟踪误差(x1-xd) (a) 控制器输入信号ud (b) 控制器输入信号uq 图4有限时间动态面反步法控制下的输入信号 (a) 控制器输入信号ud (b) 控制器输入信号uq 图5动态面控制下的输入信号 与文献[18]的动态面控制技术相比,本文引入了有限时间控制技术,加快了系统的收敛速度,减小了系统的跟踪误差,提高了系统的鲁棒性。 本文将有限时间方法和动态面反步法相结合,实现了PMSM的非线性位置跟踪控制,仿真分析结果表明,将有限时间技术与动态面反步法相结合,保留了动态面反步法的优点之外,在缩短系统收敛时间的同时,减小了系统的跟踪误差,提高了系统的鲁棒性。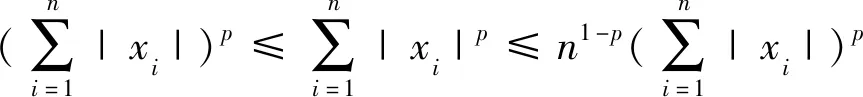
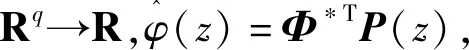
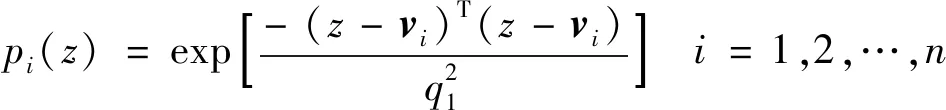
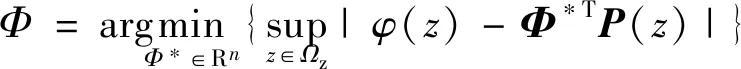
2 PMSM系统控制器设计
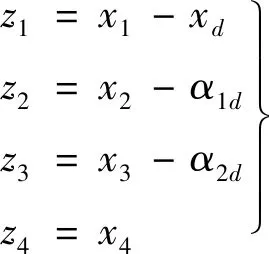
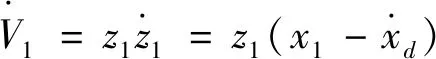


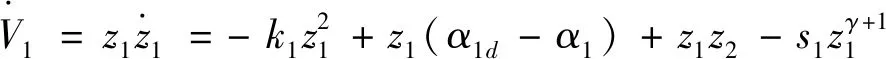
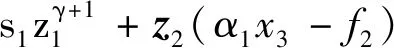
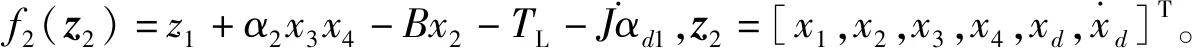
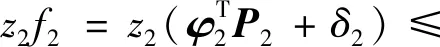
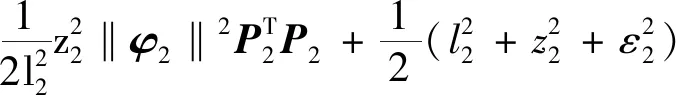
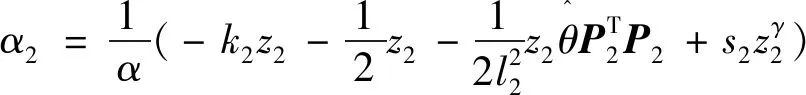
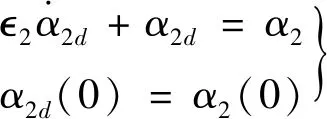

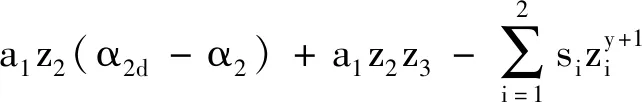
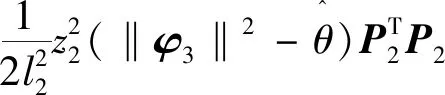
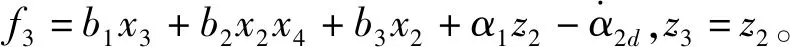

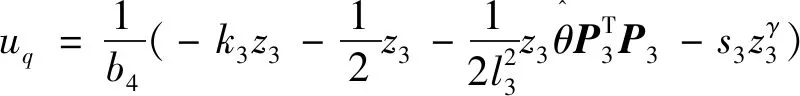
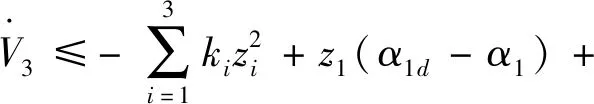

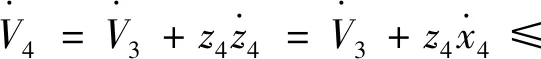

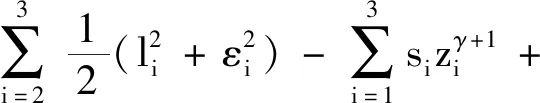


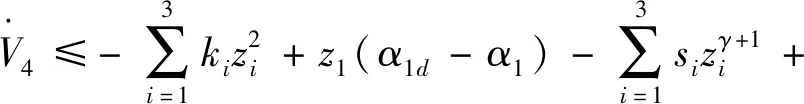
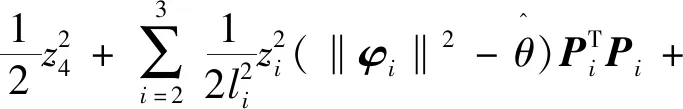
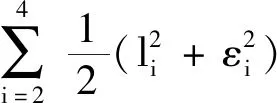
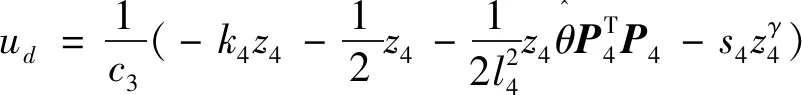
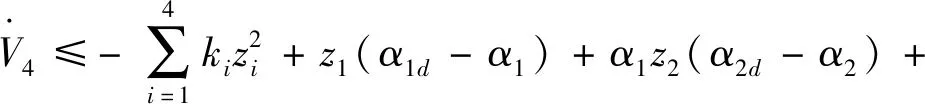
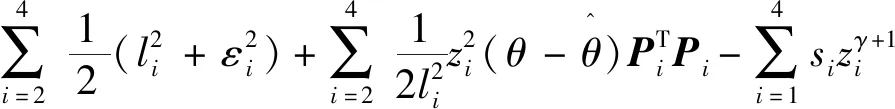

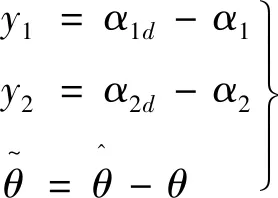


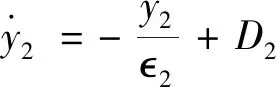
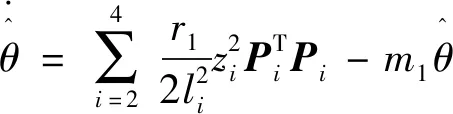
3 稳定性分析
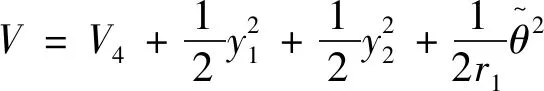
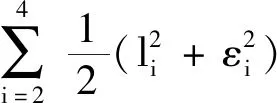

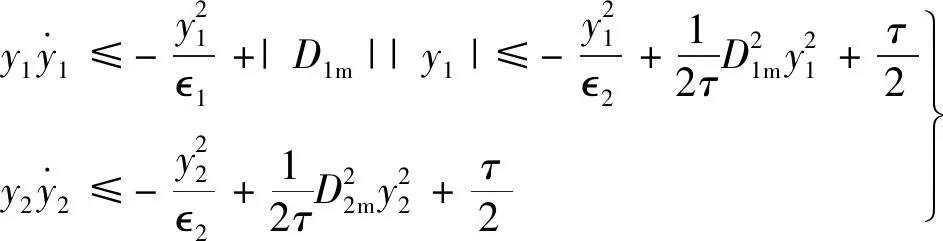
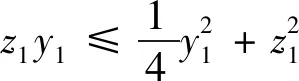
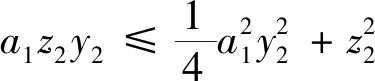
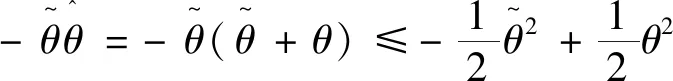
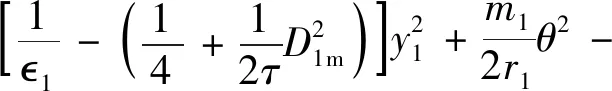
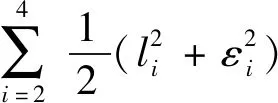

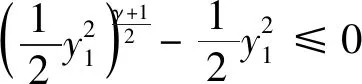

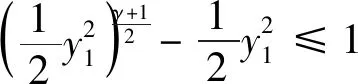
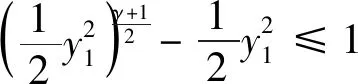
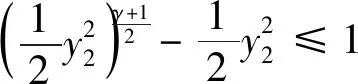
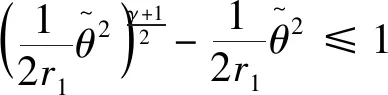
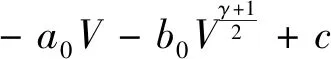
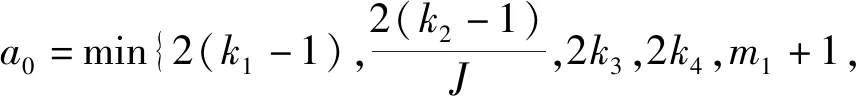
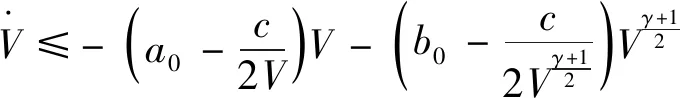
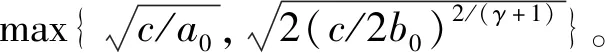
4 对比实验分析

5 结 语

