永磁同步直线电动机电流控制方法

牛宇杰，王明义，杨 瑞，李立毅

(哈尔滨工业大学 电气工程及自动化学院，哈尔滨 150001)

0 引 言

近年来，随着永磁同步电机理论的不断完善以及其驱动控制系统的不断研究，永磁同步电机已广泛应用于民用、工业、军事、航天等领域。永磁同步直线电动机也随之迅速发展，在精密数控机床、光刻机等领域中，作为直驱传动机构的核心单元，得到了广泛的应用。目前，永磁同步直线电动机的控制系统一般是三闭环系统，由内而外分别是电流闭环、速度闭环和位置闭环。电流闭环作为整个系统的最内部的闭环，对外环的速度闭环和位置闭环以及整个系统的精度均有重要影响，因此永磁同步直线电动机控制系统中的电流环必须具有较好的控制特性。

永磁同步直线电动机驱动控制系统的电流环作为系统的内环，不仅需要有较快的响应速度，而且在控制精度以及带宽方面都要有较好的性能，否则将会影响系统外环以及整个系统的动态和静态响应，由于整个系统最终是通过调节电流来控制系统的输出推力的，所以电流环精度对输出推力有直接的影响。另外，该系统存在强耦合性、强非线性和易受干扰等问题，所以在设计电流控制算法时，应该具有高度解耦、鲁棒性强、抗扰性好等特点。目前，应用较多的电流闭环控制方法主要有滞环电流控制、PI电流控制以及预测电流控制等[1]。

滞环电流控制是最早的电流控制技术，其控制简单，动态响应速度快，但控制精度差；同步旋转坐标系下的PI电流控制没有稳态误差，但带宽较低；预测电流控制理论上能够在一个周期内跟踪上指令电流，但由于数字系统存在时延加上传统预测电流控制系统对参数扰动敏感，系统鲁棒性差。许多学者对这两个问题进行了分析与改进。文献[2]和文献[3]分别针对预测电流带来的时延和参数扰动问题进行了改进。对于时延问题，其通过估算下一时刻电压值来解决；而对于参数扰动问题，其通过使用当前时刻扰动电压值来代替下一时刻扰动值解决。由于智能控制理论的不断发展，越来越多的智能控制算法也逐渐应用于电机控制算法中[4-8]。文献[4]引入鲁棒预测电流算法来提高系统的鲁棒性，降低了参数变化对系统稳定性的影响。由于滑模观测器具有较强的鲁棒性以及较快的收敛速度，所以非常适合用于补偿预测电流控制中的参数扰动[9-10]。但由于一阶滑模观测器本身存在着抖振现象，所以会对电机的动态响应产生不利影响，造成电机输出推力波动；而高阶滑模观测器由于考虑了观测器相应阶导数的设计，所以会大大减小抖振现象的影响，因而具有更好的动态响应特性。本文通过计算下一时刻电压值解决时延问题，并引入三阶超螺旋滑模观测器来估算下一时刻电流及扰动电压值以解决参数扰动问题。

本文分别应用以上三种电流闭环控制方法控制永磁同步直线电动机，并分别分析其影响因素、动静态响应以及带宽。实验结果证明，加入三阶超螺旋滑模观测器后的预测电流控制方法，大大提高了电流闭环的鲁棒性，且具有较高的控制精度和带宽，相较于滞环电流控制和PI电流控制具有更好的控制特性。

1 电流闭环控制方法

1.1 滞环电流控制

采用矢量变换的滞环电流闭环控制系统结构简单，只要有电流采样电路和基本的微处理器就可以实现，而且由于其直接通过比较反馈电流与实际电流的大小输出控制信号，不需要复杂的算法，所以电流响应速度快，鲁棒性也较好。影响滞环电流控制精度的主要因素有滞环环宽、采样频率以及电机绕组电感等。

滞环控制作为非线性控制方式，直接对电机三相电流进行闭环控制。但是，滞环电流控制也存在着很多问题，由于控制过程中开关频率不固定，谐波成分复杂，无法针对其设计滤波器，使得电机的控制精度无法提升，这导致滞环电流控制无法满足精密驱动控制的要求。为此，文献[11]和文献[12]中使用固定频率以及变占空比的方法来克服开关频率不固定的问题，但这增加了算法的复杂度，没有获得大规模应用。

由于本次设计所用到的电机绕组为三相星形绕组，没有中性线引出，实际三相电流在任意时刻是平衡的，所以只要控制其中两相电流即可[13]。考虑到功耗问题，选择不对电流最大的一相进行斩波控制，根据指令电流正负来决定该相开关管的状态。本文首先利用滞环电流控制方法实现电机闭环电流控制，然后研究滞环环宽以及采样频率对控制系统的影响，并分析和测试整个控制系统的带宽。

1.2 同步旋转坐标系下的PI电流控制

PID控制器是目前应用最广的控制器，其中包括比例、积分、微分环节。作为传统自动控制理论中最重要的控制方法，PID控制器可以达到较高的控制精度、较大的带宽，并且控制算法也相对简单，实用性非常强。

同步旋转坐标系下的PI电流控制，具有恒定的开关频率，解决了滞环电流控制中开关频率不固定、谐波成分复杂、滤波器难以设计的问题，并且通过坐标变换，该方法能够直接控制电机电流的励磁分量与推力分量，实现了电机电流的解耦，提高了系统的响应速度、控制精度以及带宽。

由于PI电流控制存在着以上所述的优点，其在工业控制领域得到了广泛应用，并且到现在仍然是最成熟、应用最多的控制方法。但其也存在着一些问题，坐标变换虽然实现了三相电流的解耦，但并没有完全将交直轴电流解耦；而且传统的PI电流控制鲁棒性差，带宽较低，虽然适用于一般的应用场合，但无法满足超精密系统的要求。

在实际测试时，先对系统的PI参数进行整定，然后分析开关频率对控制系统的影响，并测试此控制系统的带宽。

1.3 预测电流控制

预测电流控制器在理论上能够在一个控制周期内跟踪上给定电流，可以解决同步旋转坐标系下PI电流控制中的交直轴电流耦合以及反电动势干扰的问题，且可以达到较高的带宽，所以逐渐得到更多学者的研究应用。

然而，传统预测电流控制方法需要电机参数以及运行状态的准确信息，当计算所用到的参数与电机运行时的实际参数不匹配时，电机的响应会与理想情况有很大差异。并且，在一般情况下，由于电机参数(电阻、电感、磁链)在电机运行时会随着温度、电流等级以及工作频率的变化而变化，所以电机的准确参数是无法测量的。另外，当使用DSP实现传统预测电流时，由于数字系统存在延时，所以也会给电流响应带来一定的影响。针对时延和参数扰动这两个问题，本文采用以下的方法进行了优化设计。

1.3.1 时延问题的解决

传统的预测电流控制器输出电压是由下式来计算的：

I(k+2)=M·I(k+1)+B·[V(k+1)-Ψ]

(2)

式中：I，V，M，B和Ψ分别为电流矩阵、电压矩阵、两个系数矩阵以及磁链矩阵。由以上两式可以估算出第k+1周期的输出电压：

由于系统在一个控制周期内电流上升有最大值，所以应该对指令电压进行限幅，以免指令电压过大导致实际电流无法准确跟踪指令电流。经过限幅后的指令电压值可由下式计算：

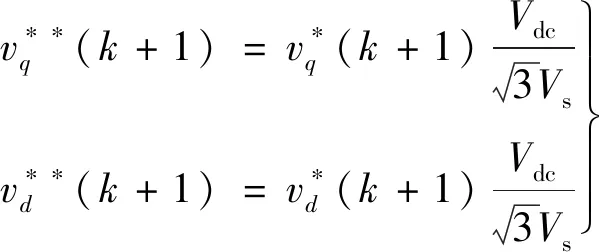
(4)

式中：Vs为交轴与直轴电压矢量的合成值。

1.3.2 参数扰动问题的解决

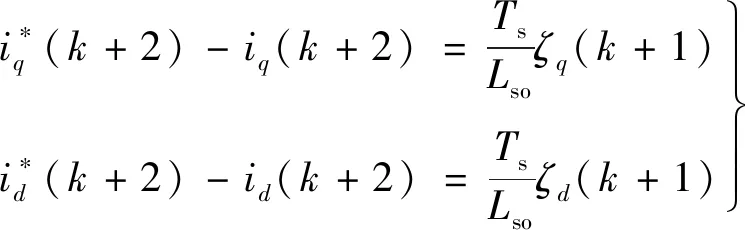
(5)

式中：ζq,ζd分别为交、直轴的扰动电压值[14]。

如果扰动是由电阻变化(电阻变化值为ΔR)引起的，并且其他参数保持不变，则电流的跟踪误差可简化为下式：

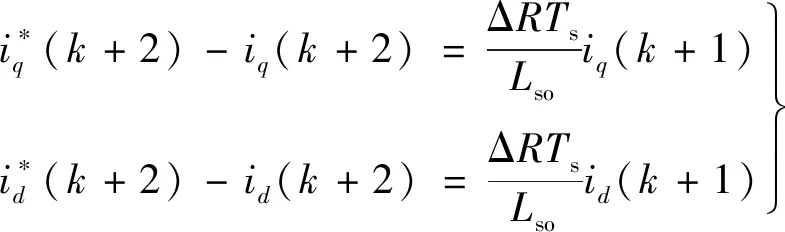
(6)

从式(6)中可以看出，当电阻变化时，电流响应存在一个稳态误差，且误差值与ΔR成正比，因此，电阻变化会对电流响应产生不利影响。

如果扰动是由电感变化(电感变化值为ΔL)引起的，且其他参数保持不变，则电流的跟踪误差可以简化为下式(7)：

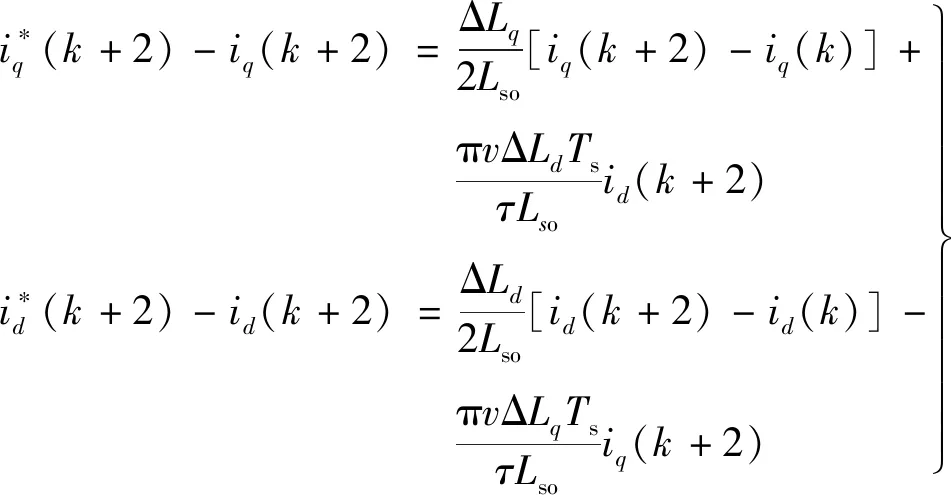
(7)

分析式(7)可知，当仅有电感扰动时，电流偏差与电流变化率和运行速度有关。

当仅有电机磁链发生变化时(磁链变化值为Δλf)，电流的跟踪误差可以简化:

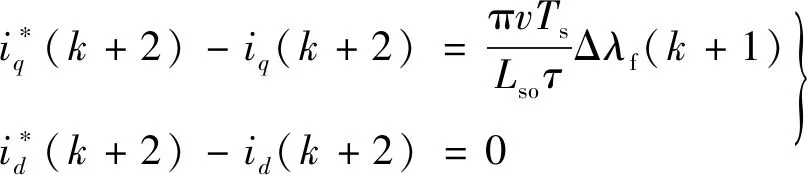
(8)

从式(8)中可以看出,直轴电流并不会受磁链变化的影响，但交轴电流误差与电机实际运行速度有关。

由以上分析可知，下一时刻电流以及扰动的估算值的精确程度会直接影响预测电流控制的控制效果。因此，为了解决参数扰动对预测电流控制的影响，设计一个三阶超螺旋滑模观测器来估算下一时刻电流及扰动电压值。由于电磁推力与交轴电流呈正比，并且本次设计采用id=0的控制策略，所以这里以交轴电流为例分析三阶超螺旋滑模观测器的设计。

根据上面的分析，考虑扰动在内的电流方程可以由下式表示：

《城市绿线管理办法》《城市规划编制办法》等一系列部门规章，覆盖了风景园林行业的规划设计、组织管理、景观保护等方面，通过行政介入与政府引导的方式有效地加强了风景园林规划建设的运行与管理。

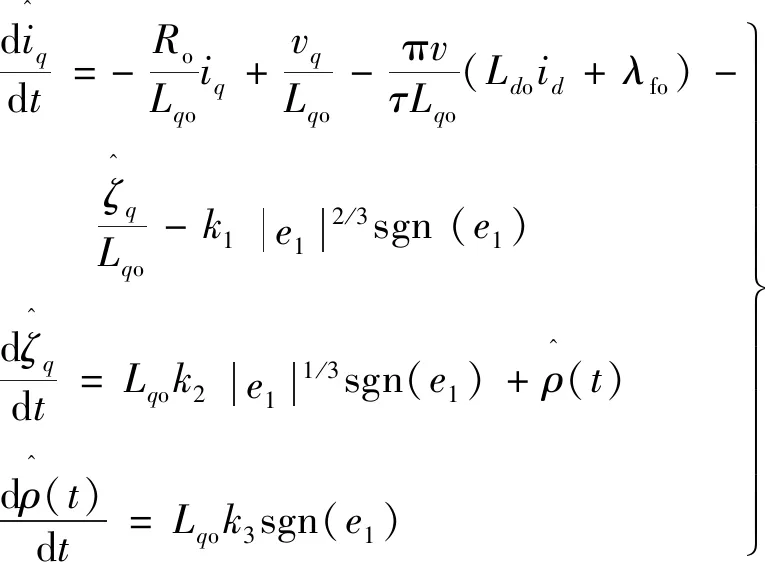
(9)

定义以下3个状态误差：

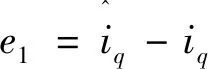
(10)

(11)

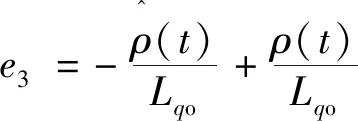
(12)

在起始时刻，可以设置交轴电流估计值与实际值相等，误差估计值为零，且ρ(t0)=0。误差的动态表达式如下式：

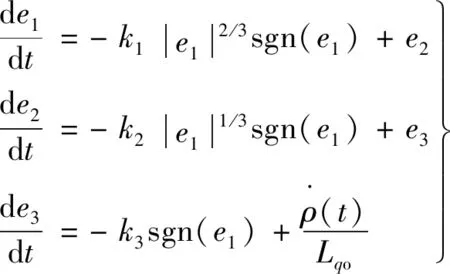
(13)

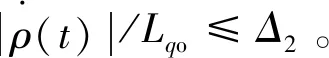
预测电流控制的控制系统框图如图1所示。本文首先利用传统的预测电流控制方法实现对电机的电流闭环控制，然后分析时延补偿以及扰动补偿对控制系统的影响，最后测试整个控制系统的带宽。

图1 永磁同步直线电动机驱动控制系统实验平台

2 电流闭环控制实验研究

2.1 实验平台简介

本文的实验平台构成主要包括：实验用永磁同步直线电动机、设计的驱动控制器、仿真器、万用表、交流调压器、示波器、PC机等，软件采用CCS6.1进行编程。本文设计使用的永磁同步直线电动机的主要参数如表1所示，实验用永磁同步直线电动机如图2 (a)所示，驱动控制器如图2(b)所示。

表1 实验用永磁同步直线电动机主要参数

(a) 实验用永磁同步直线电动机

(b) 驱动控制器实物图

本文的永磁同步直线电动机绕组为三相星形绕组，没有中性线引出；用到的位置传感器为光栅尺。

2.2 实验结果

2.2.1 滞环电流控制实验研究

首先，对两相斩波控制进行实验分析。实验时，给定交轴电流指令为2.5 Hz、幅值为1 A的方波电流，滞环环宽设置为±20 mA，采样频率设置为20 kHz，死区时间设置为2 μs,得到的实验结果如图3(a)所示。

然后，改变两相斩波滞环控制的环宽和采样频率，分析滞环电流控制的影响因素，得到的实验结果如图3(b)、图3(c)所示。图3(b)为将环宽改为±100 mA的实验波形，可以看出，开关频率明显降低，且电流误差明显变大；图3(c)为将采样频率改为10 kHz时的实验波形，可以看出，相较于采样频率为20 kHz时开关频率也有所降低，且电流误差也有一定程度增加，这些结果与前述理论分析一致。

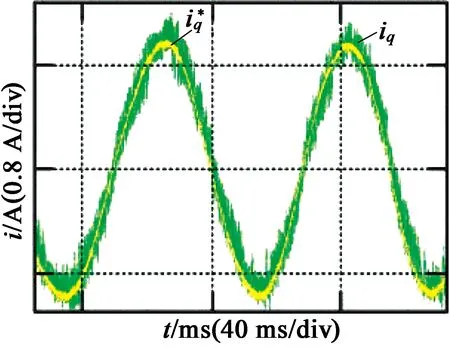
(a) 两相斩波滞环控制

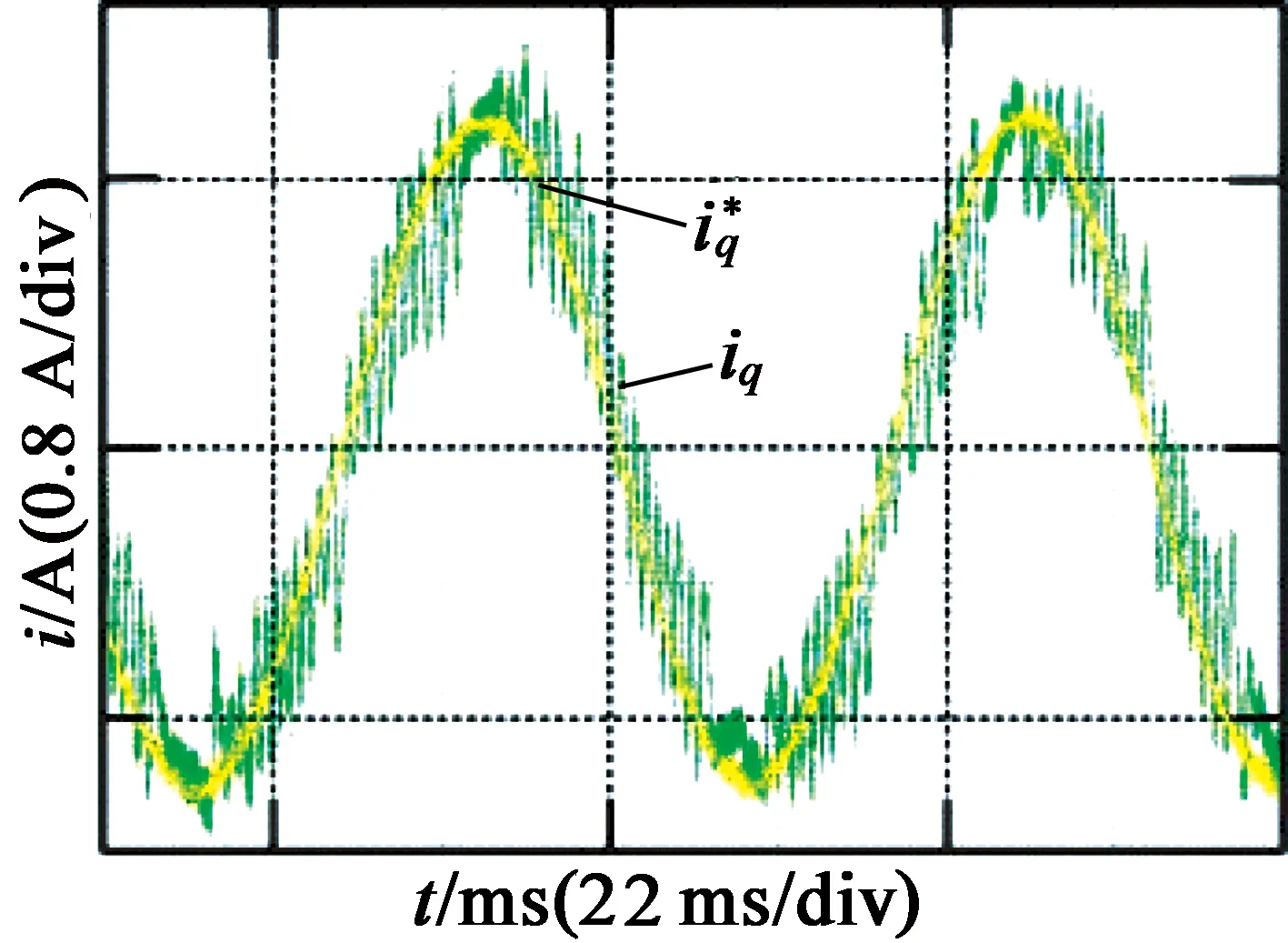
(b) 变环宽实验结果

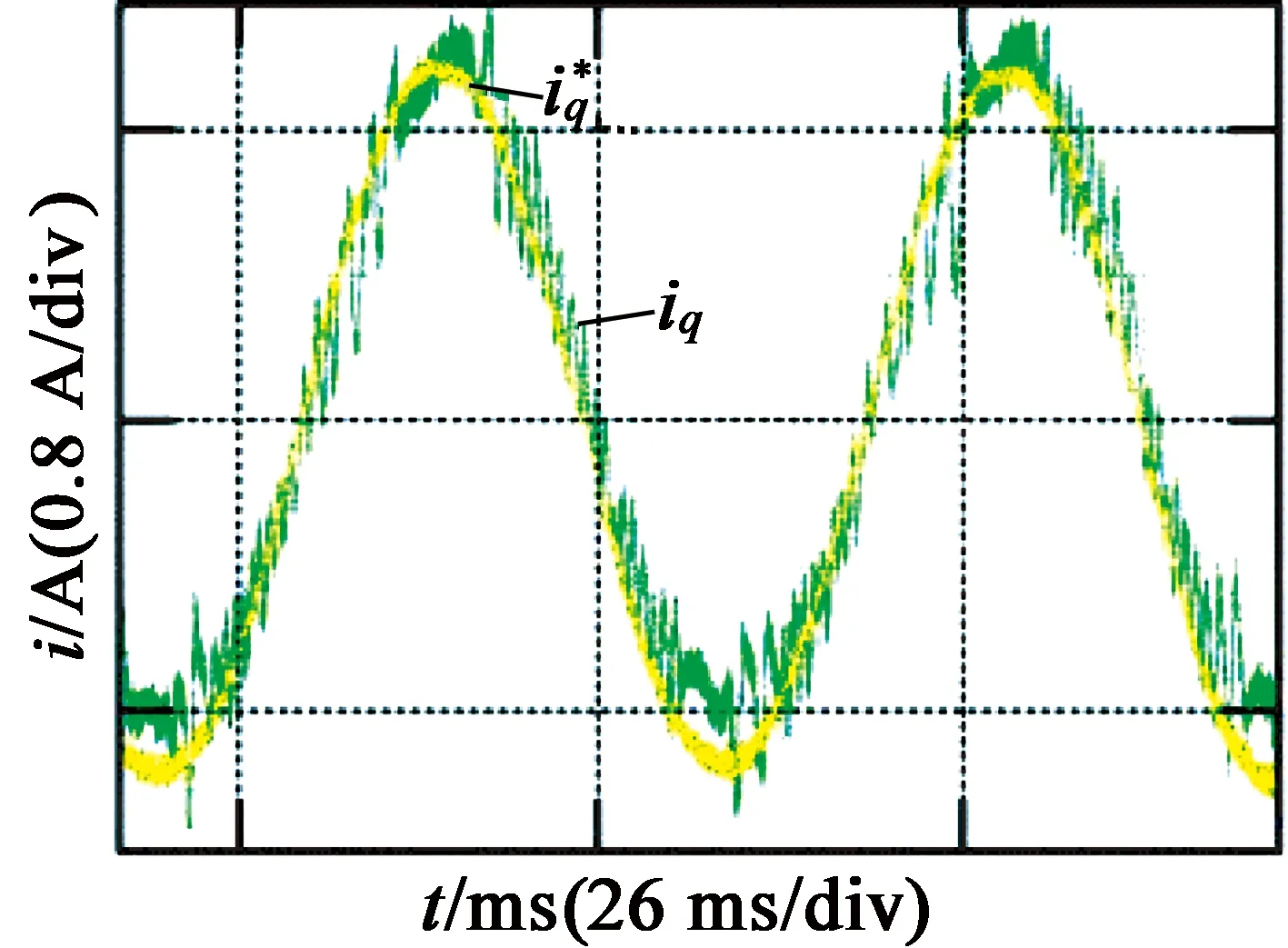
(c) 变采样频率实验结果

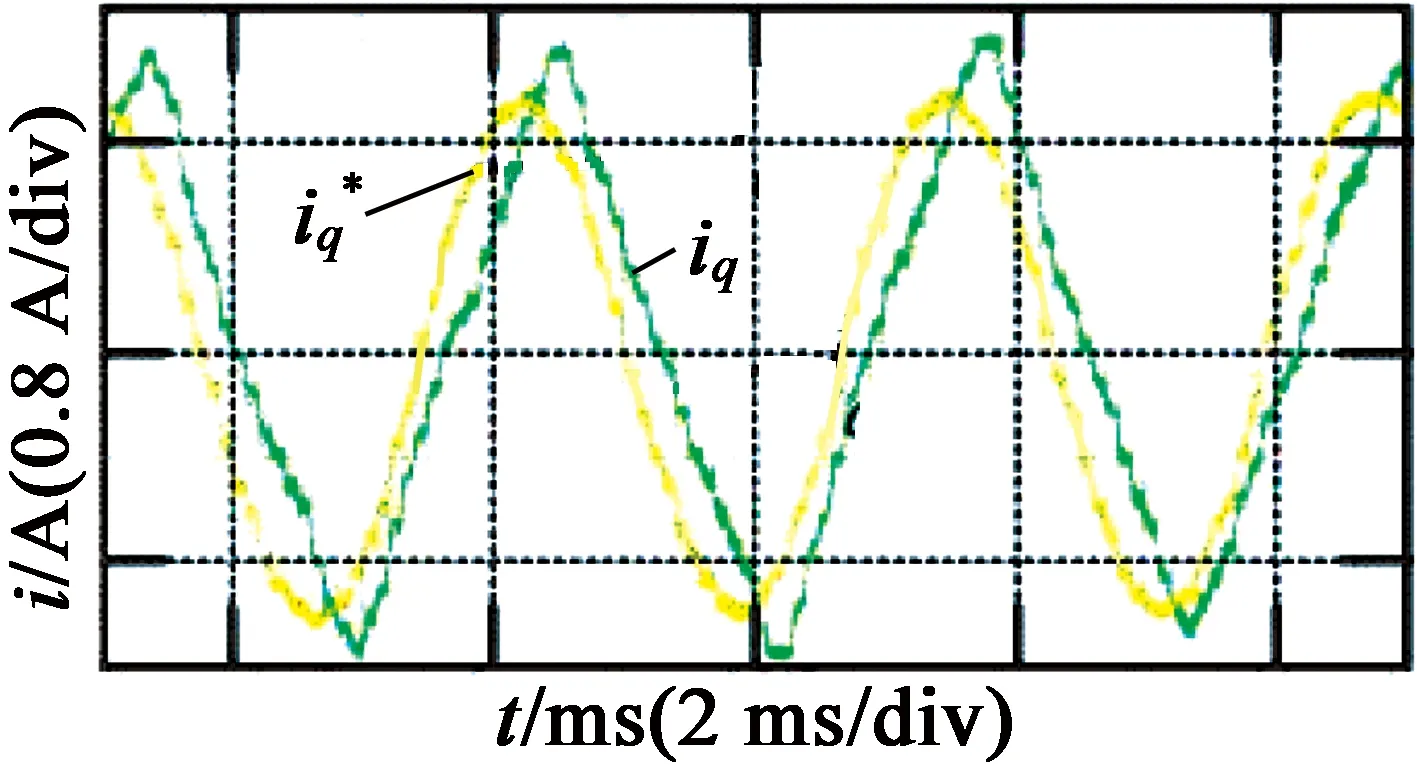
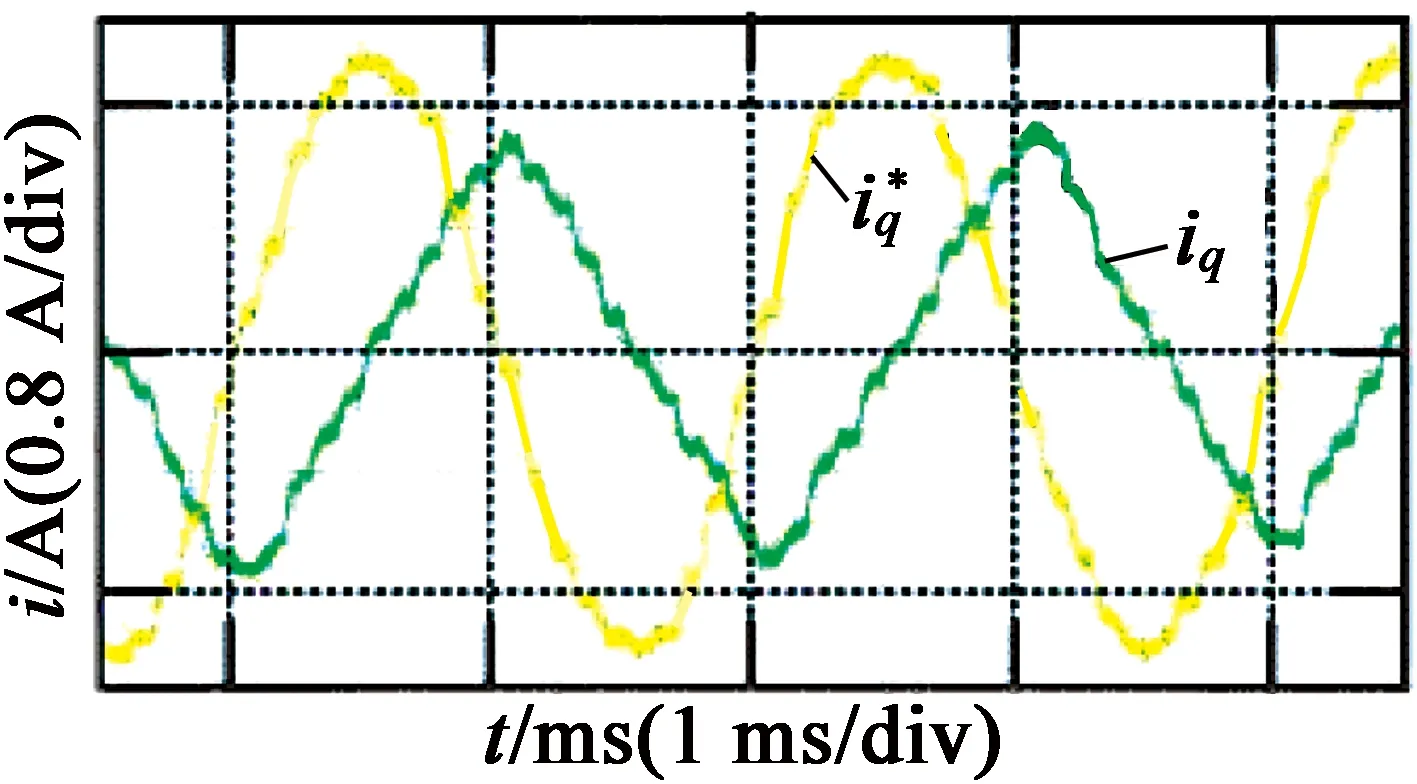
图4为滞环电流控制的带宽实验结果。可以看出，在指令电流频率为500 Hz时，相位滞后基本达到90°，幅值衰减不严重，该系统的带宽为500 Hz左右。由于实验仅使用传统意义上的滞环电流控制，电流波动很大。

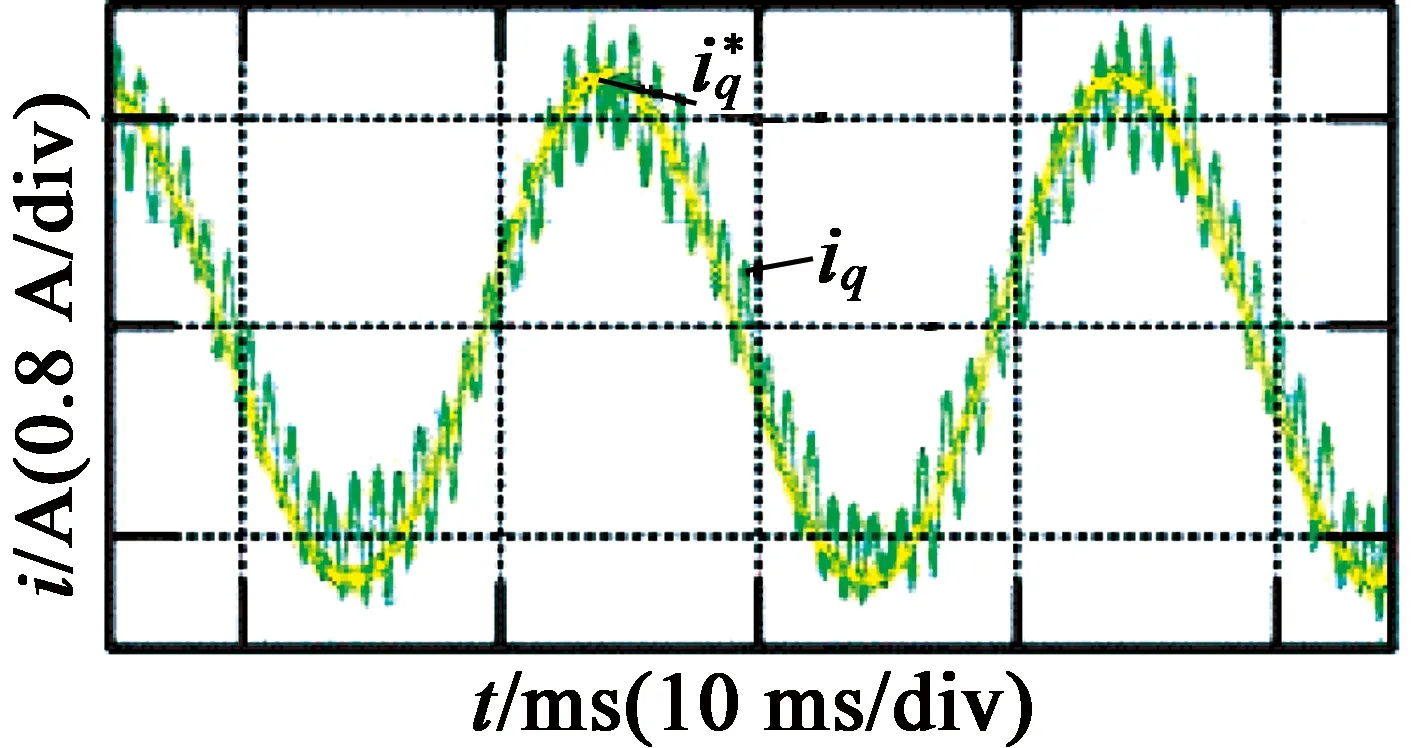
(a) 50 Hz

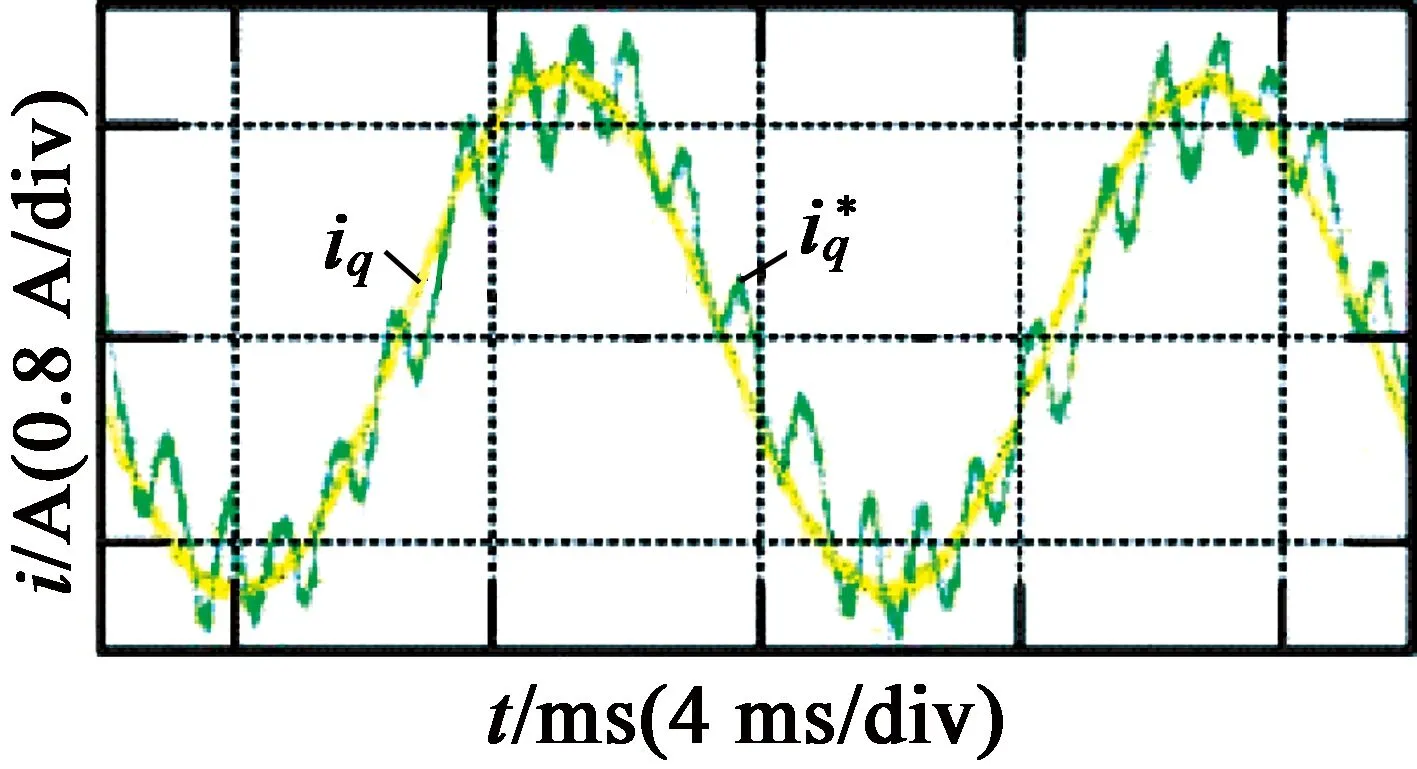
(b) 100 Hz

(c) 300 Hz

(d) 500 Hz

图4滞环电流控制带宽实验结果

由以上分析可知，滞环电流控制系统响应速度快，带宽较高，动态性能好，但控制精度差。

2.2.2 同步旋转坐标系下PI电流控制实验研究

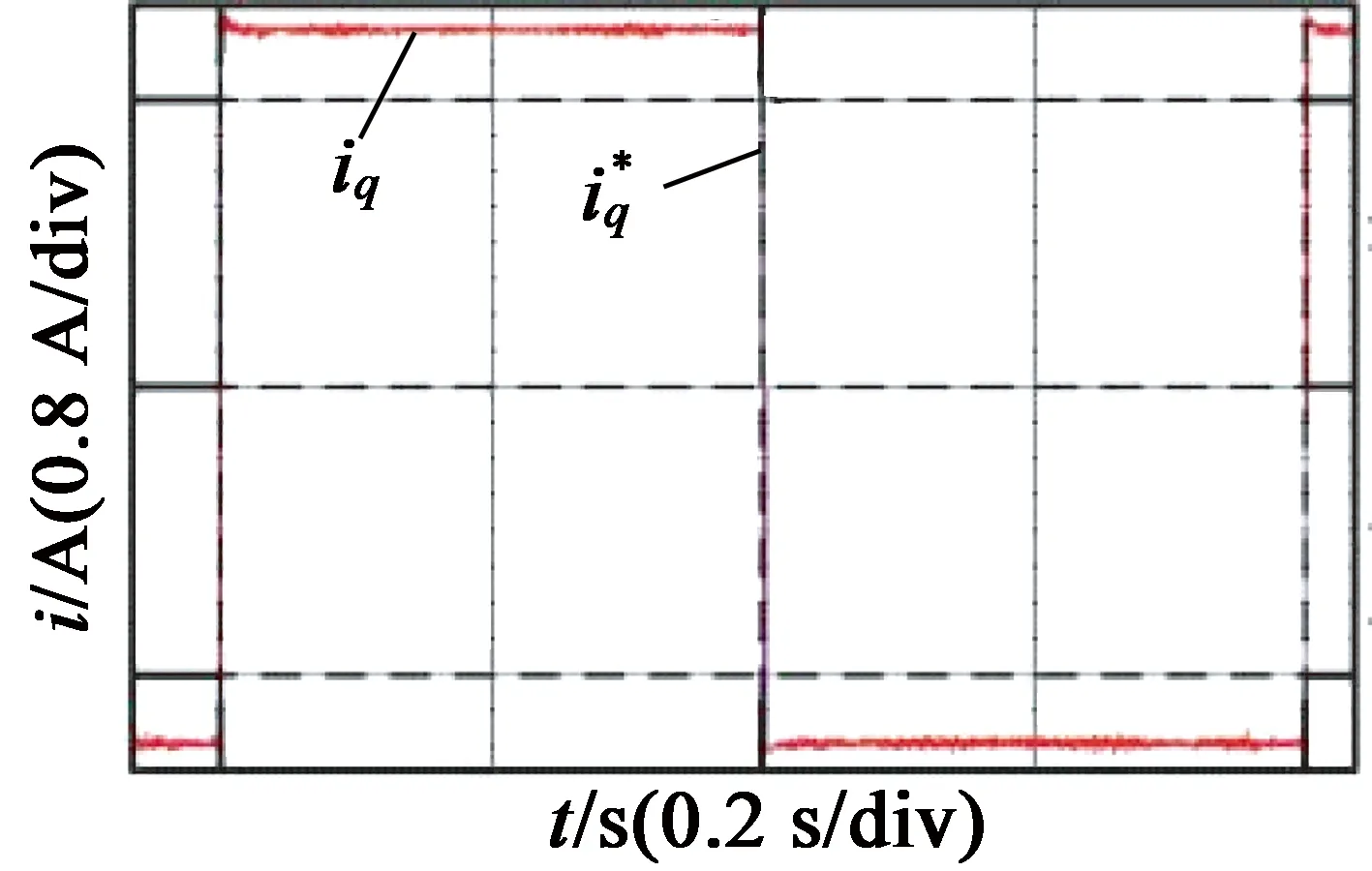
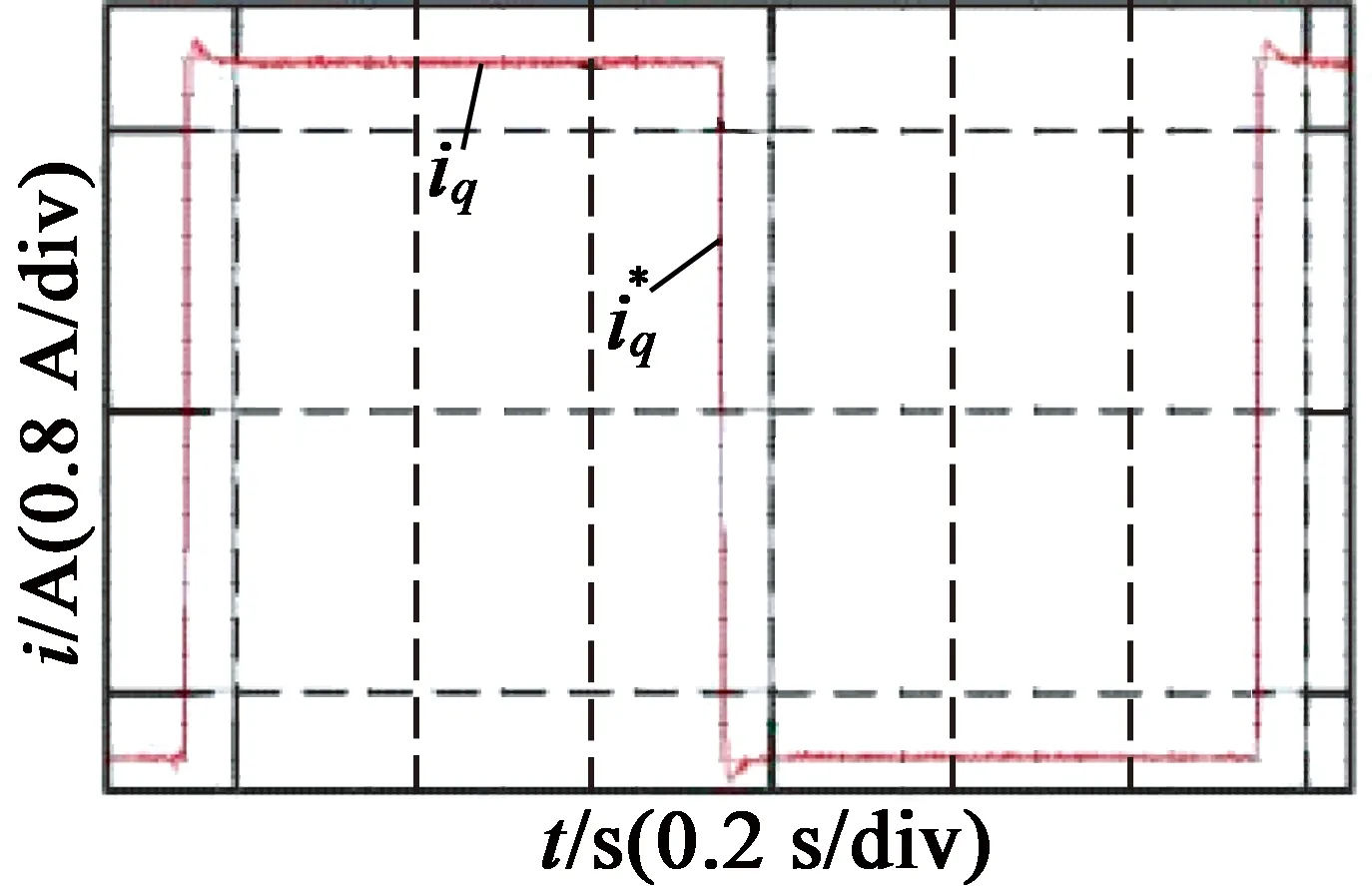
对实验平台的PI参数进行整定，调整控制器中PI参数，使得整个系统的阶跃响应有较小的超调、较快的上升时间以及较小的电流波动。经过多次实验，最终得到本次实验平台电流环的PI参数：Kp=11，Ki=0.035。

改变开关频率得到的PI电流闭环测试实验结果如图5所示。可以看出，电流上升时间、电流误差及超调量等均未出现明显变化。

(a) 开关频率为5 kHz时阶跃响应

(b) 开关频率为10 kHz时阶跃响应

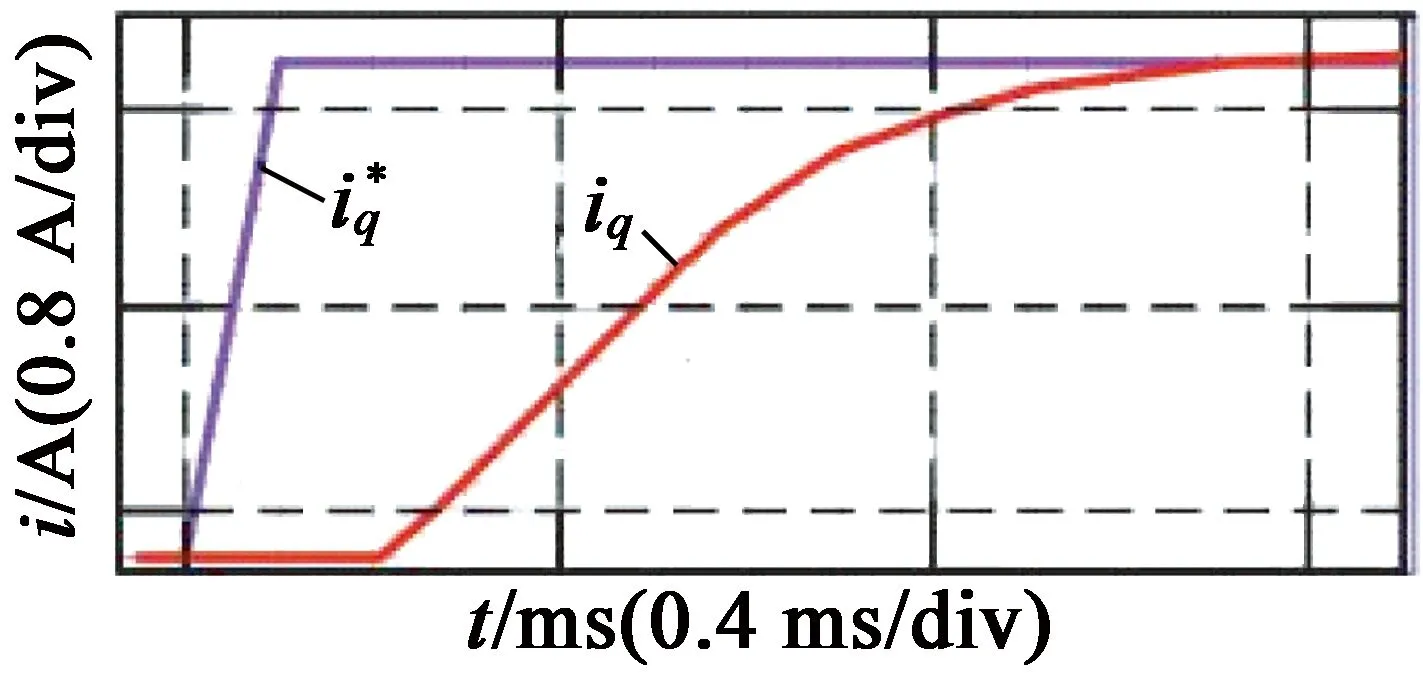
(c) 开关频率为5 kHz时局部放大

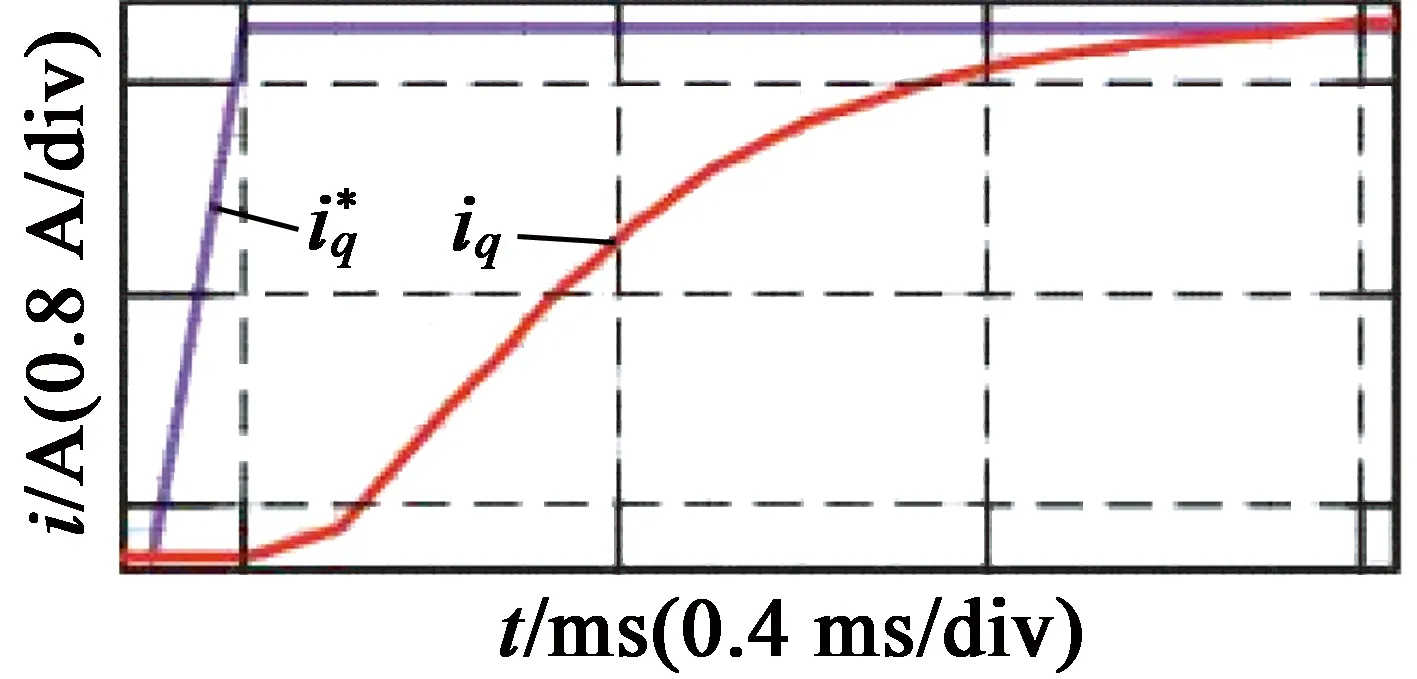
(d) 开关频率为10 kHz时局部放大

图5PI电流闭环测试实验结果

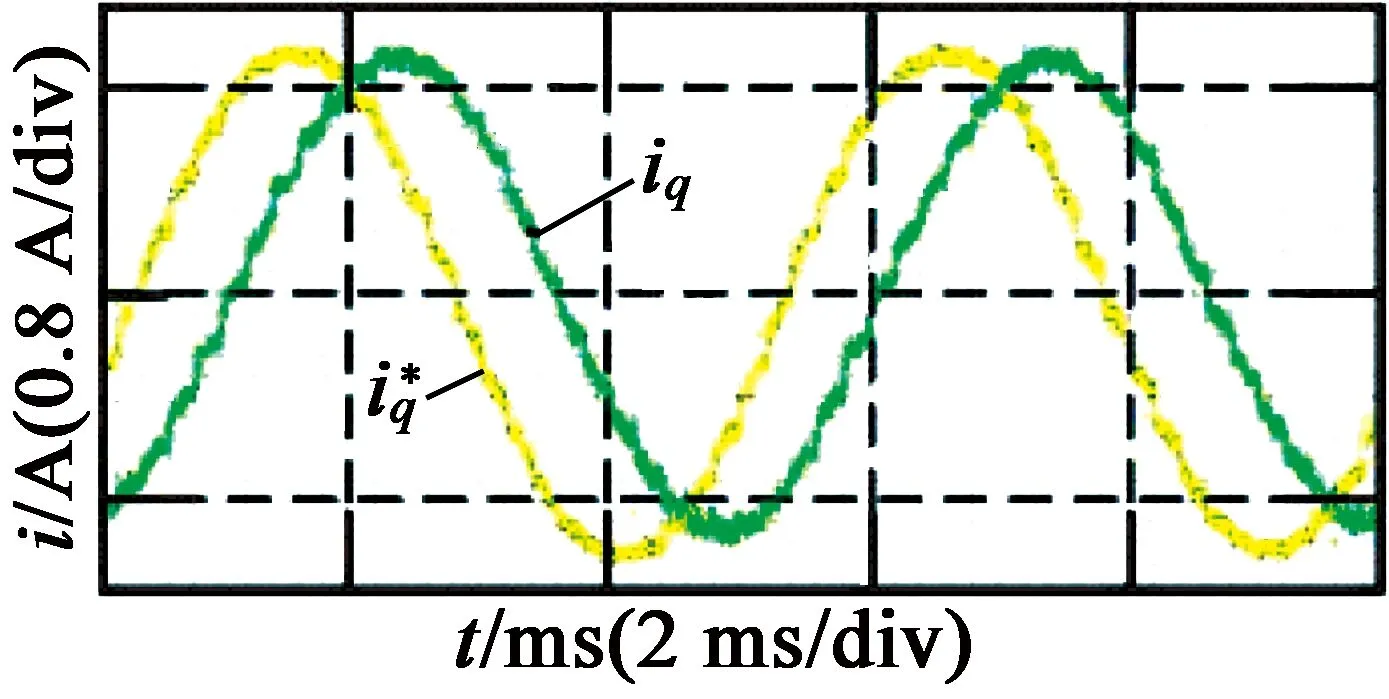
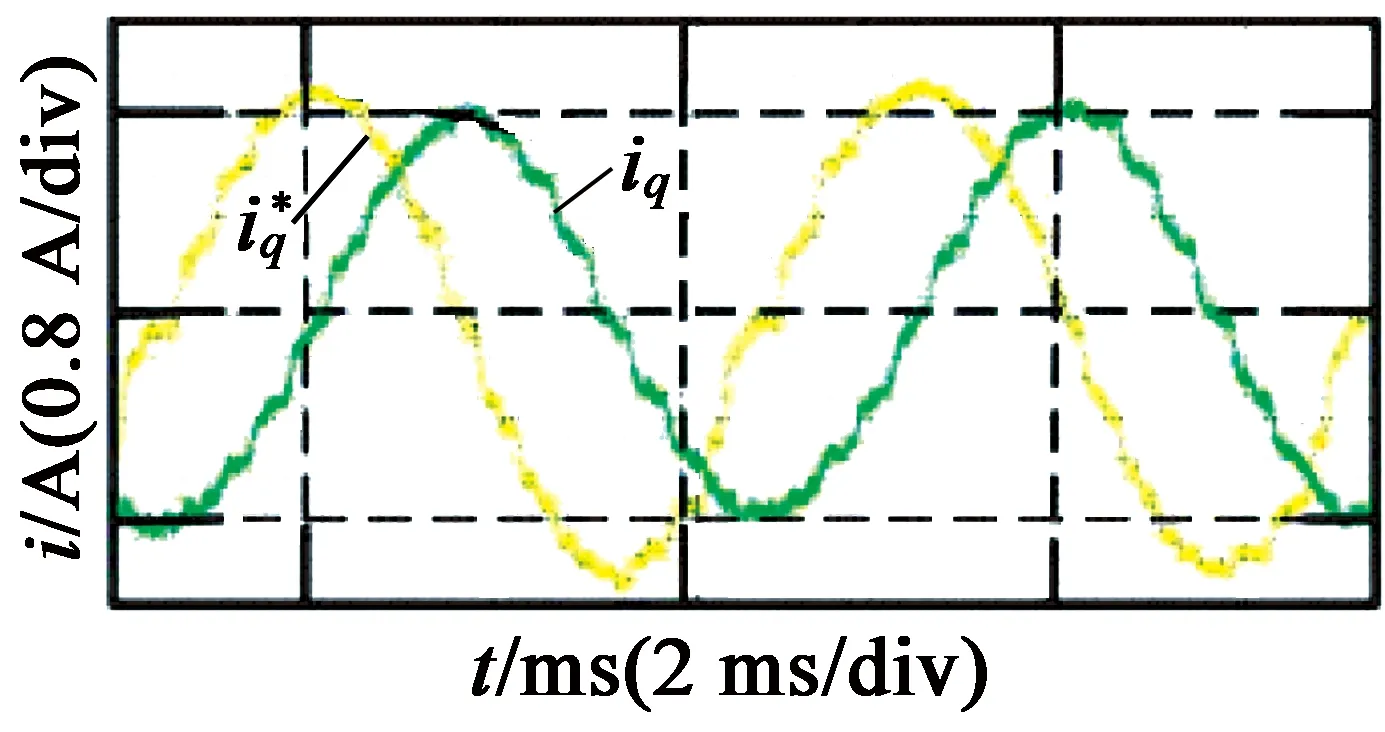
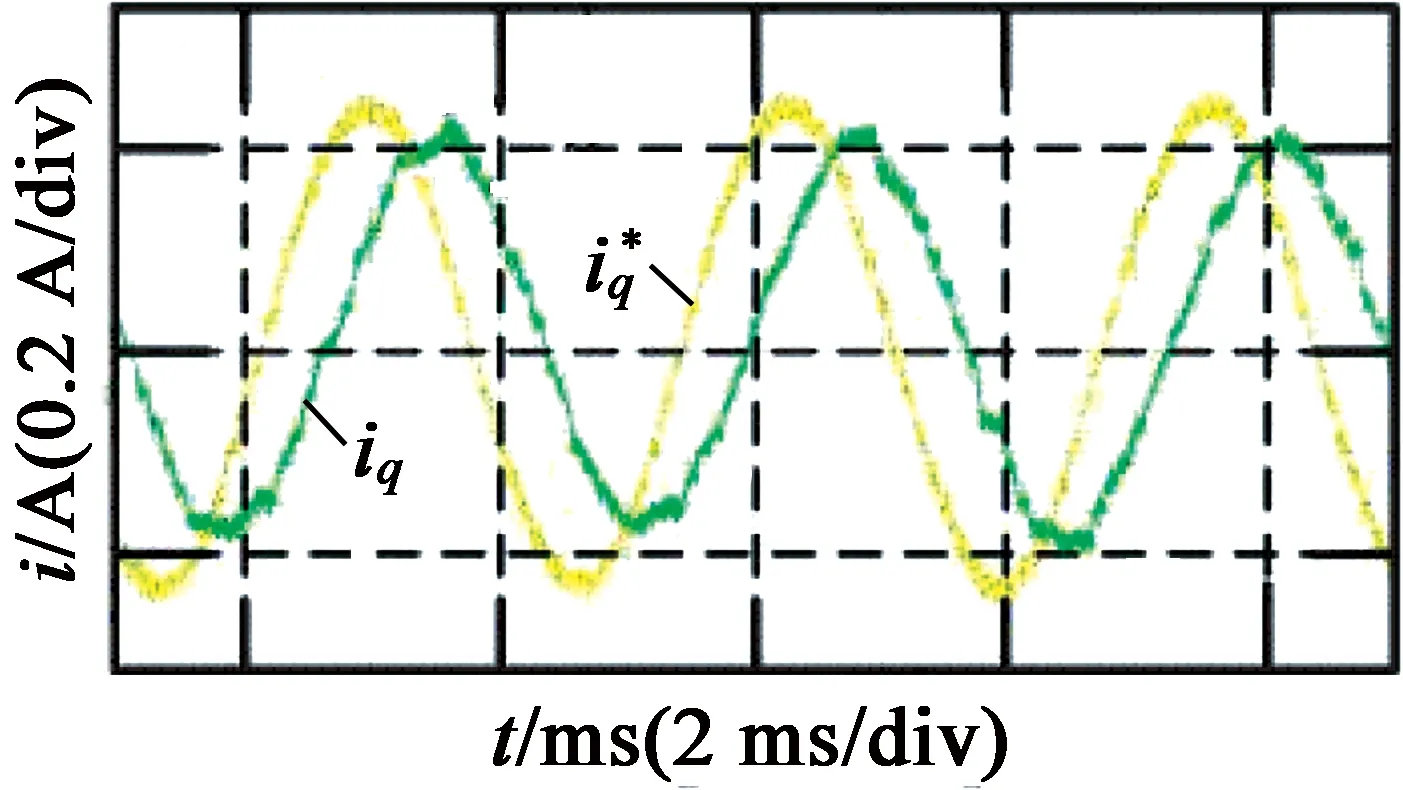
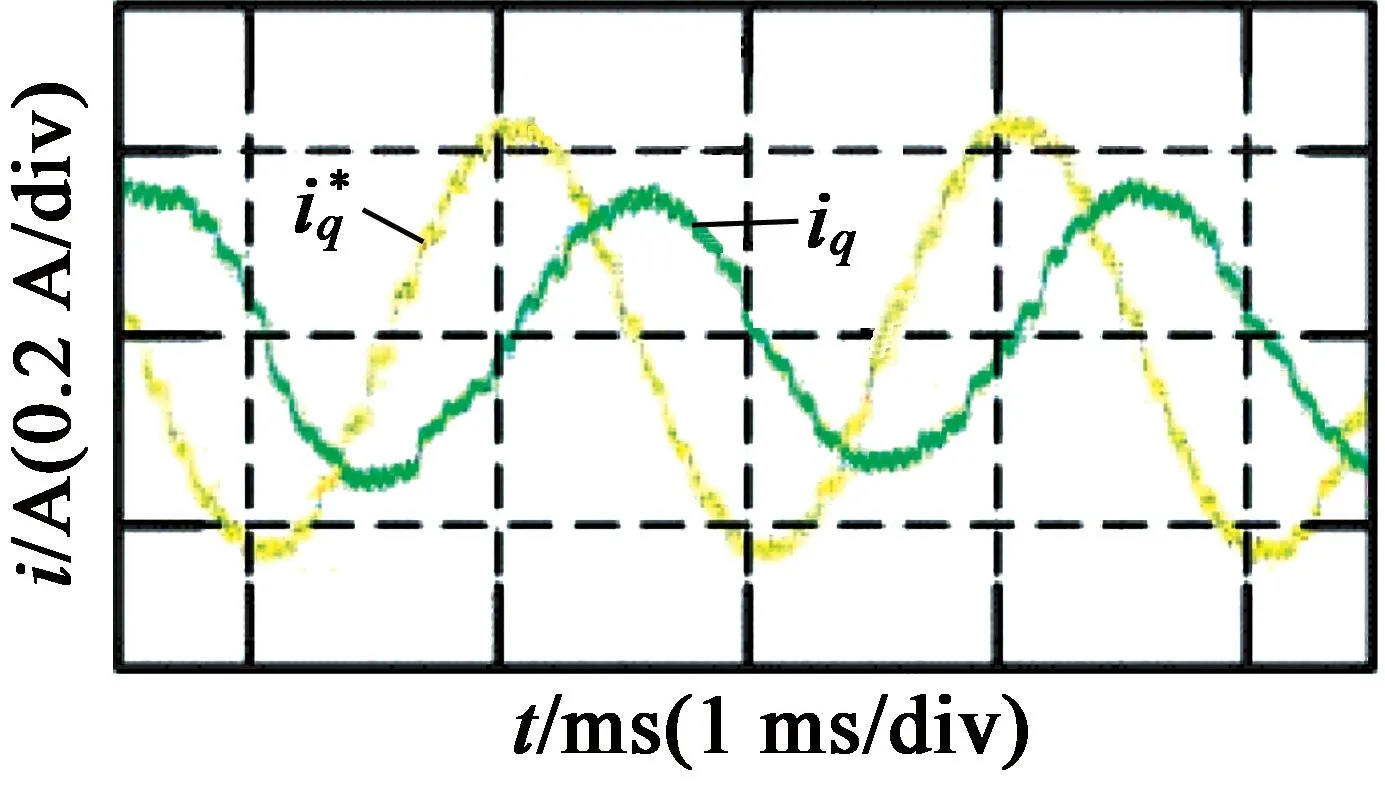
图6和图7分别为开关频率为5 kHz和10 kHz时的带宽测试实验结果。从图6、图7中可以看出，电流响应相位滞后严重，在开关频率为5 kHz时，系统带宽为300 Hz左右；在开关频率为10 kHz时，实际电流相位滞后要比5 kHz时少，但相位滞后仍然比较明显，此时系统的带宽为500 Hz左右。

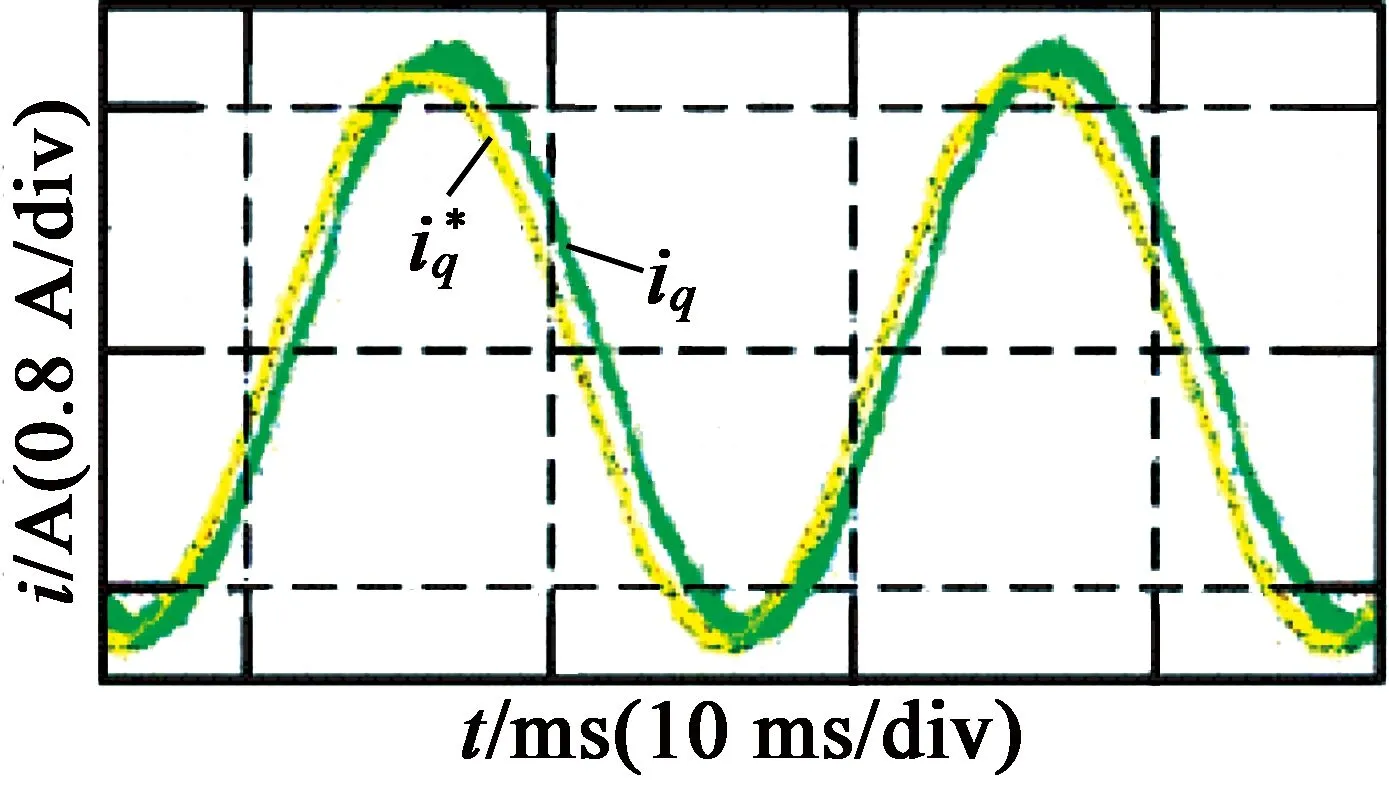
(a) 50 Hz

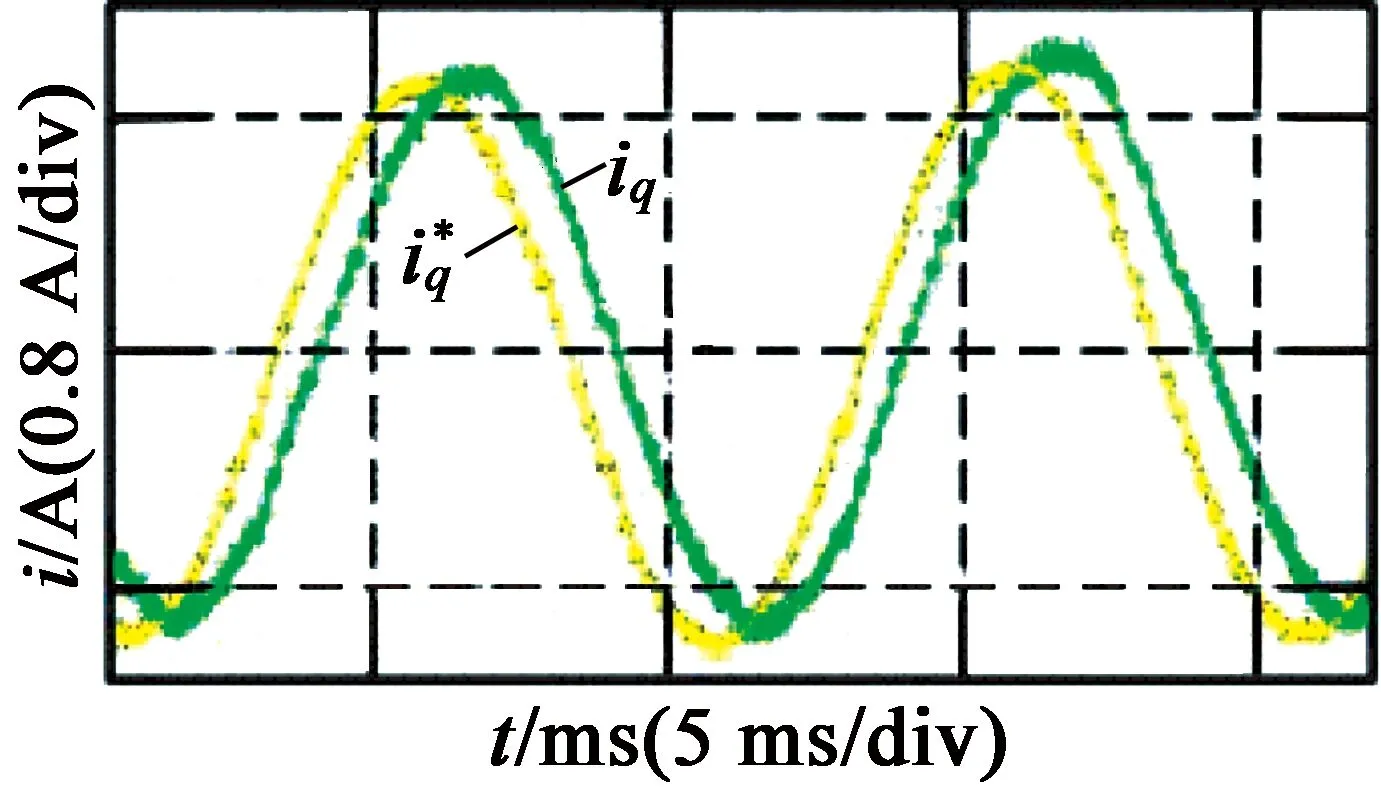
(b) 100 Hz

(c) 200 Hz

(d) 300 Hz

图6开关频率为5 kHz时的带宽测试结果

(a) 50 Hz

(b) 100 Hz

(c) 300 Hz

(d) 500 Hz

图7开关频率为10 kHz时的带宽测试结果

从以上实验结果可以看出，PI电流控制没有稳态误差，当PI参数合理时，电流误差、响应速度等动静态指标较好，且控制精度较好，但其控制系统的带宽较低，且控制系统对PI参数的依赖性较大；当PI参数不匹配时，控制效果较差。

2.2.3 预测电流控制实验研究

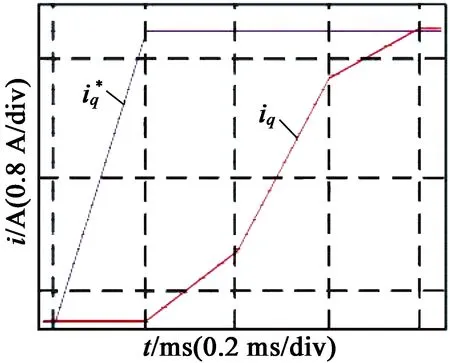
预测电流控制实验与PI电流闭环测试类似，交轴电流指令输入幅值为1 A、频率为2.5 Hz的方波。传统预测电流要求参数匹配度较高，当参数不匹配时，存在很大的超调和振荡；改变控制器中电机参数至参数匹配时的实验结果如图8(a)、图8(c)所示，可以看出，参数匹配时，电机电流可以达到零稳态误差，且上升时间很短，从-1 A到1 A的上升时间大约为1 ms，但电流的阶跃响应存在着较大的超调量，使得电机运行噪声较大。

加入延时补偿后的实验结果如图8(b)、图8(d)所示，此时的电流阶跃响应上升时间略有增加，大约为1.6 ms，但不存在超调和静差，电流噪声也很小，基本能够实现控制系统的要求，但整个系统对参数扰动很敏感。

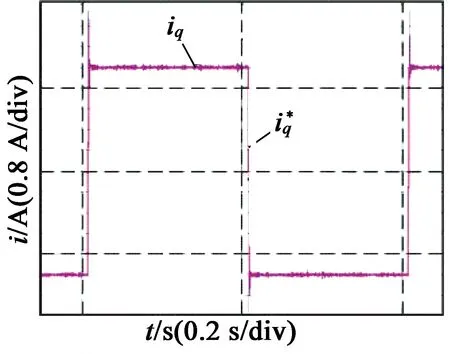
(a) 传统预测电流参数匹配阶跃响应

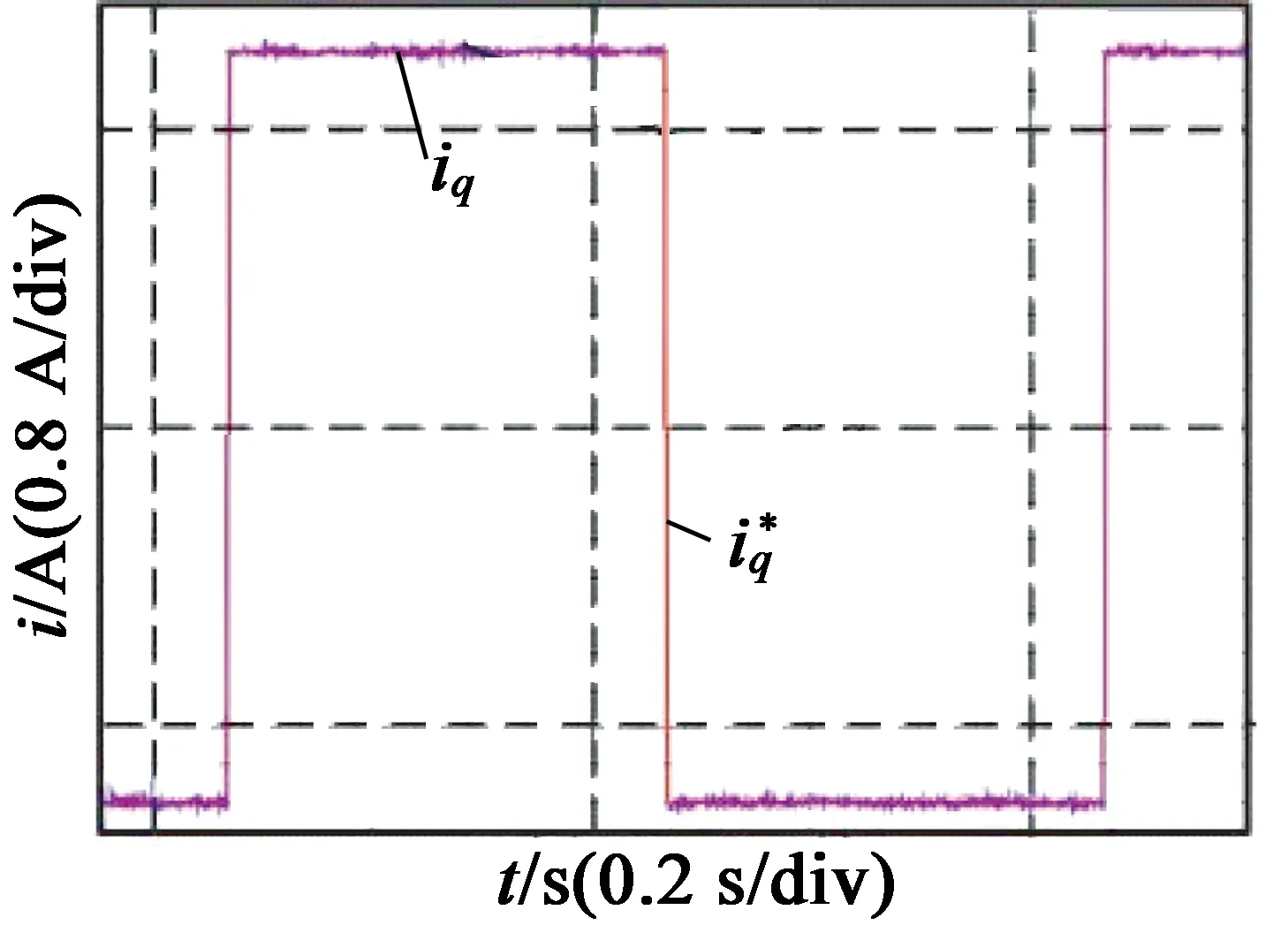
(b) 加时延补偿后阶跃响应

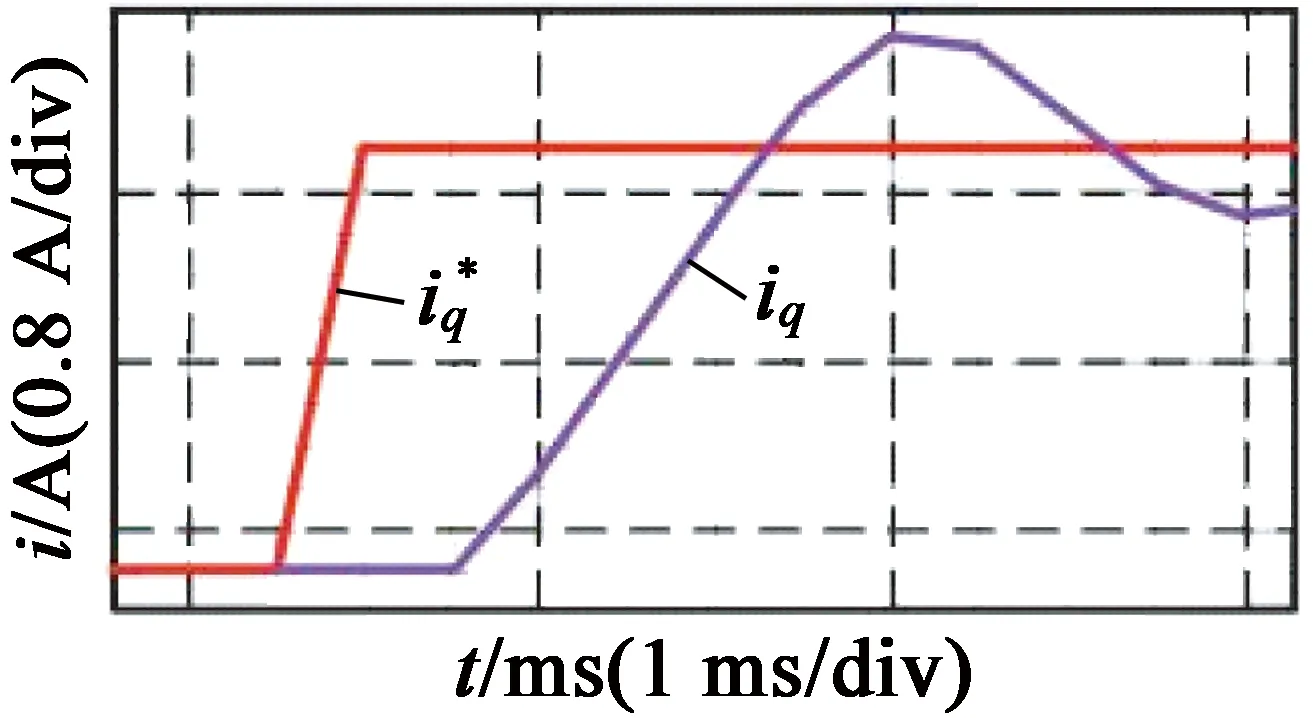
(c) 传统预测电流参数匹配局部放大

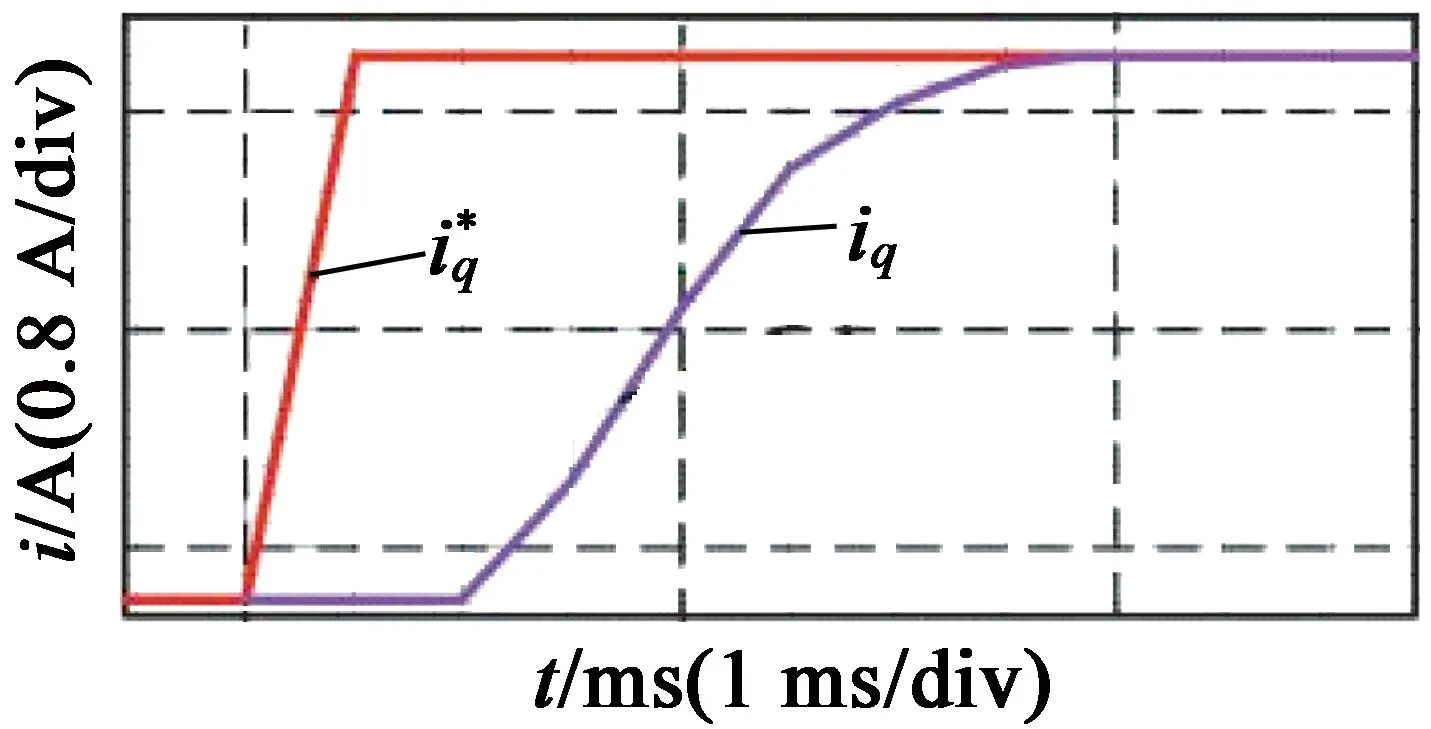
(d) 加时延补偿后局部放大

图8传统预测电流及加时延补偿实验结果

图9为加入延时补偿，改变控制器中电机参数后的实验结果。可以看出，当存在较大的参数扰动时，电机的电流阶跃响应可能会存在静差、超调或畸变的现象。

图9(a)为改变控制器中的电阻值时的实验结果。可以看出，电流响应出现稳态误差，且误差大小与ΔR(控制器中电阻值与电机实际电阻值的差值)成正比。

图9(b)为改变控制器中磁链值时的实验结果，可以看出当控制器中磁链增大时，电机速度较低时，存在着一个负的电流偏差；随着电机速度增加，电流偏差逐渐减小至零，之后随着电机速度增加，电流偏差变为一个正值，并逐渐增大；反之，情况与之正好相反。

图9(c)、图9(d)为改变控制器中电感值时的部分实验结果。分析实验结果可知，增大控制器中电感值时，电流的阶跃响应不存在稳态误差，且上升时间减小，但出现了超调现象，且控制器中电感越大，超调越大，上升时间越短；反之，减小控制器中电感值时，阶跃响应仍然不存在稳态误差，无超调，但上升时间变得很大，大约为3.2 ms，且控制器中电感值越小，上升时间越长。

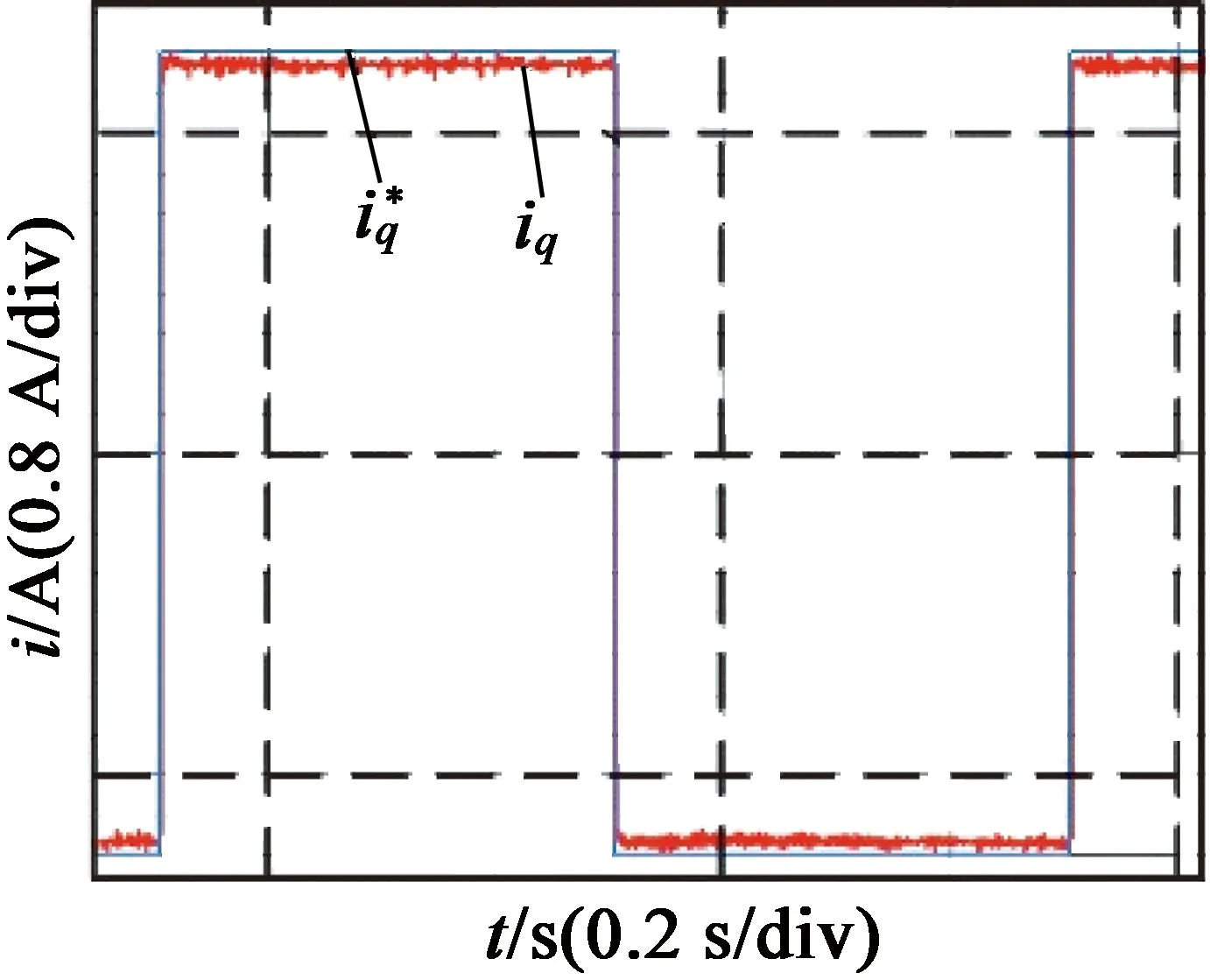
(a) R控制器=0.7R实际阶跃响应

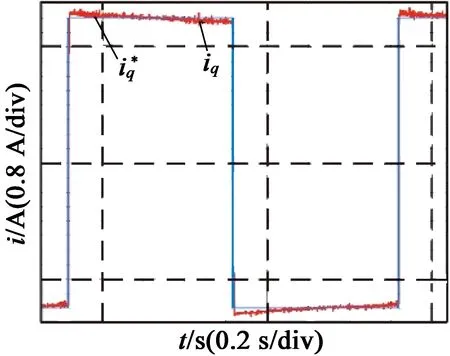
(b) ψ控制器=0.7ψ实际阶跃响应

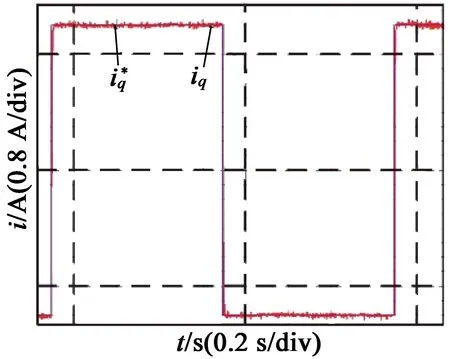
(c) L控制器=0.7L实际阶跃响应

(d) L控制器=0.7L实际局部放大

图9未加扰动补偿时改变控制器中参数实验结果

这些实验结果与理论分析所得到的结论一致。由以上分析可知，预测电流控制在参数匹配时加入时延补偿后基本能够达到控制系统的要求，但该系统对参数扰动敏感，系统鲁棒性差，为此，利用设计的三阶超螺旋滑模观测器来补偿扰动值，对观测器中的参数进行整定，经过多次试验，当k1=40，k2=14 000，k3=50 000且参数匹配时得到的实验结果波形图如图10所示。可以看出，电流不存在稳态误差和超调，电流上升时间很快，且电机运行时噪声也很小。由以上分析可以看出，当参数匹配时，扰动补偿器的加入并没有使之前的驱动控制系统的动、静态响应变坏。

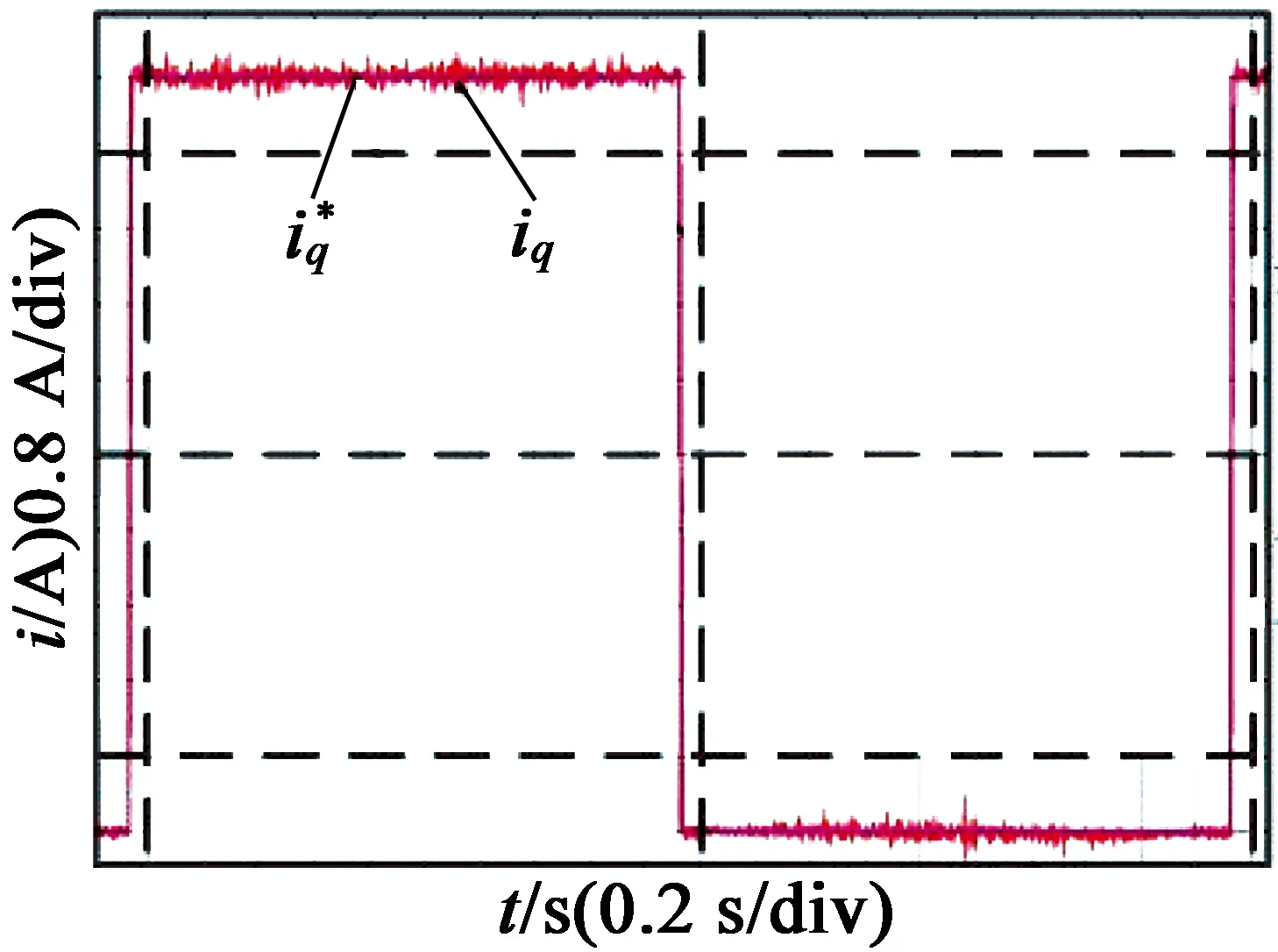
(a) 加扰动补偿时阶跃响应

(b) 加扰动补偿时局部阶跃响应大

图10加时延和扰动补偿参数匹配实验波形

对该系统的鲁棒性进行测试。重复之前对只加入时延补偿系统鲁棒性测试的实验过程，部分实验结果如图11所示。可以看出，改变控制器中的电阻、电感以及磁链时，电机的阶跃响应不会存在稳态误差，且没有超调和振荡，电流上升时间也很小，可以基本达到参数匹配时的控制效果。由以上分析可知，加入时延和扰动补偿后的预测电流控制系统不仅具有较好的控制精度和响应速度，而且此系统抗扰性提升，鲁棒性增强。

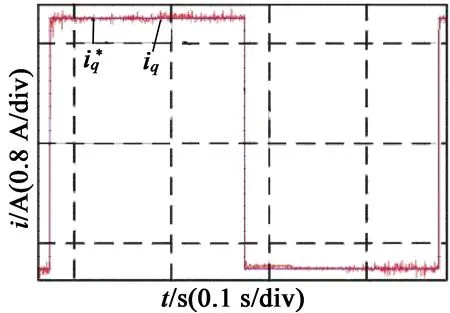
(a) R控制器=0.7R实际阶跃响应

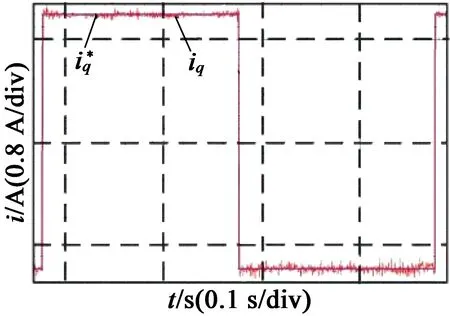
(b) ψ控制器=0.7ψ实际阶跃响应

(c) L控制器=0.7L实际阶跃响应

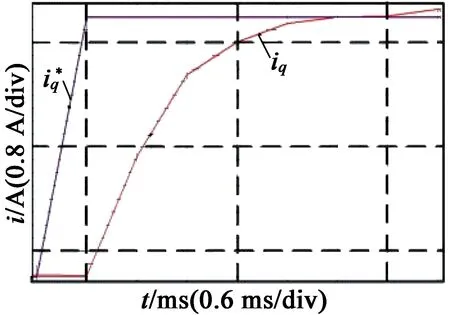
(d) L控制器=0.7L实际局部放大

图11加入扰动补偿后改变控制器中参数实验波形

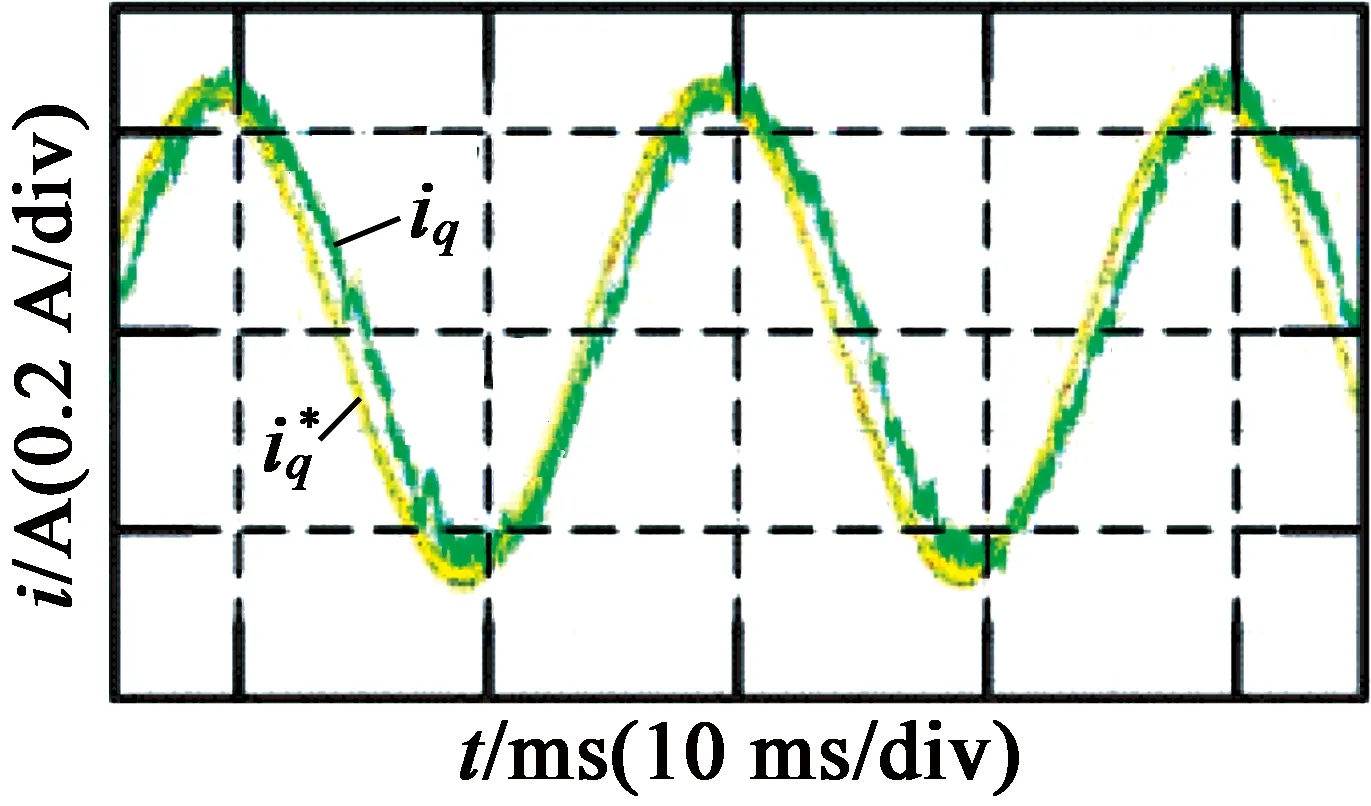
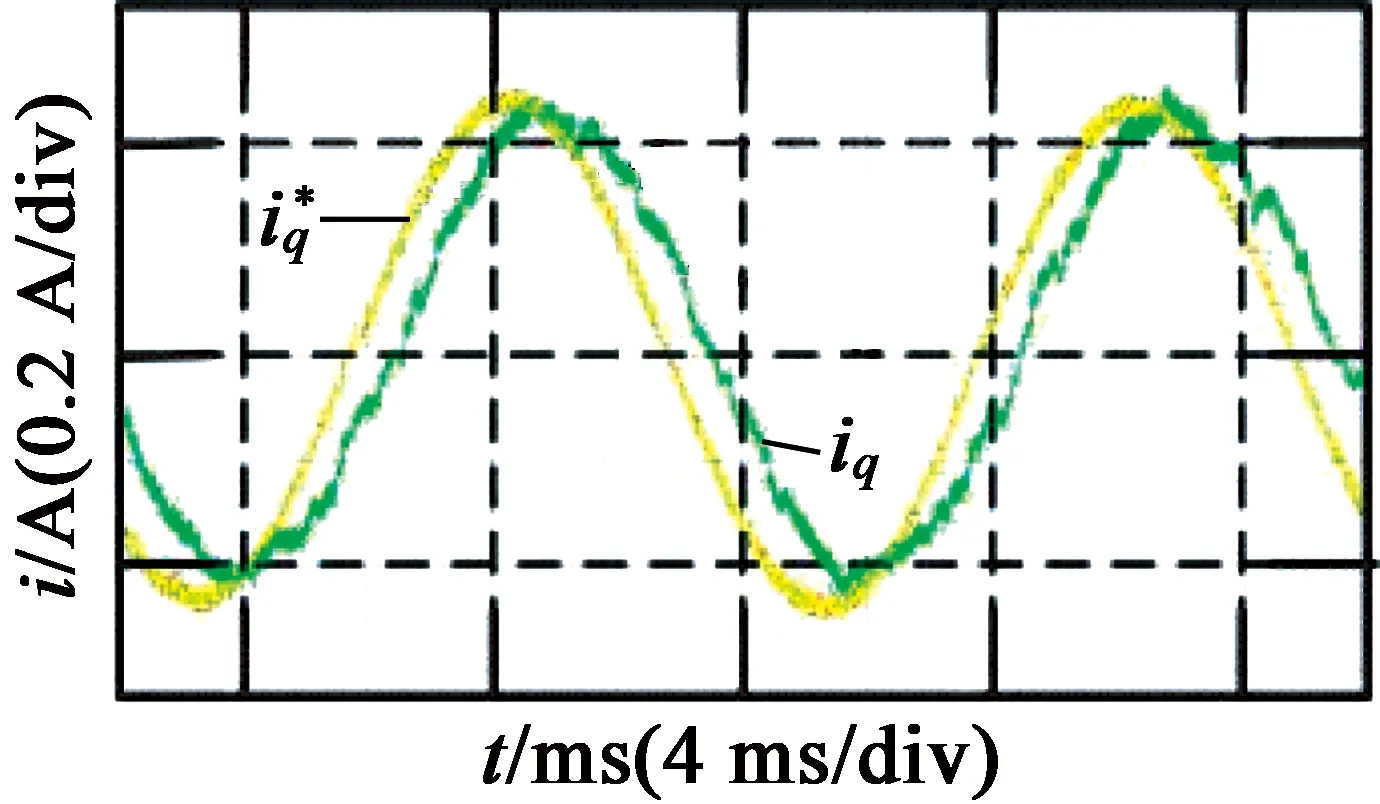
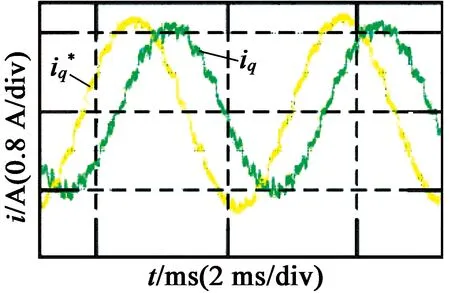
图12为预测电流闭环控制系统的带宽测试结果。可以看出，在开关频率为5 kHz时的控制系统带宽约为500 Hz。

由上述分析可知，预测电流控制器加入三阶超螺旋滑模观测器补偿时延和扰动后，系统的鲁棒性提升，且动态响应较快，控制系统的带宽以及控制精度都具有较高的水平。

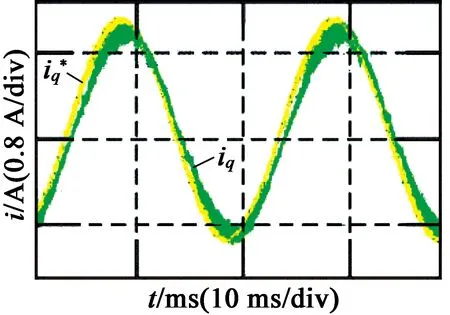
(a) 50 Hz

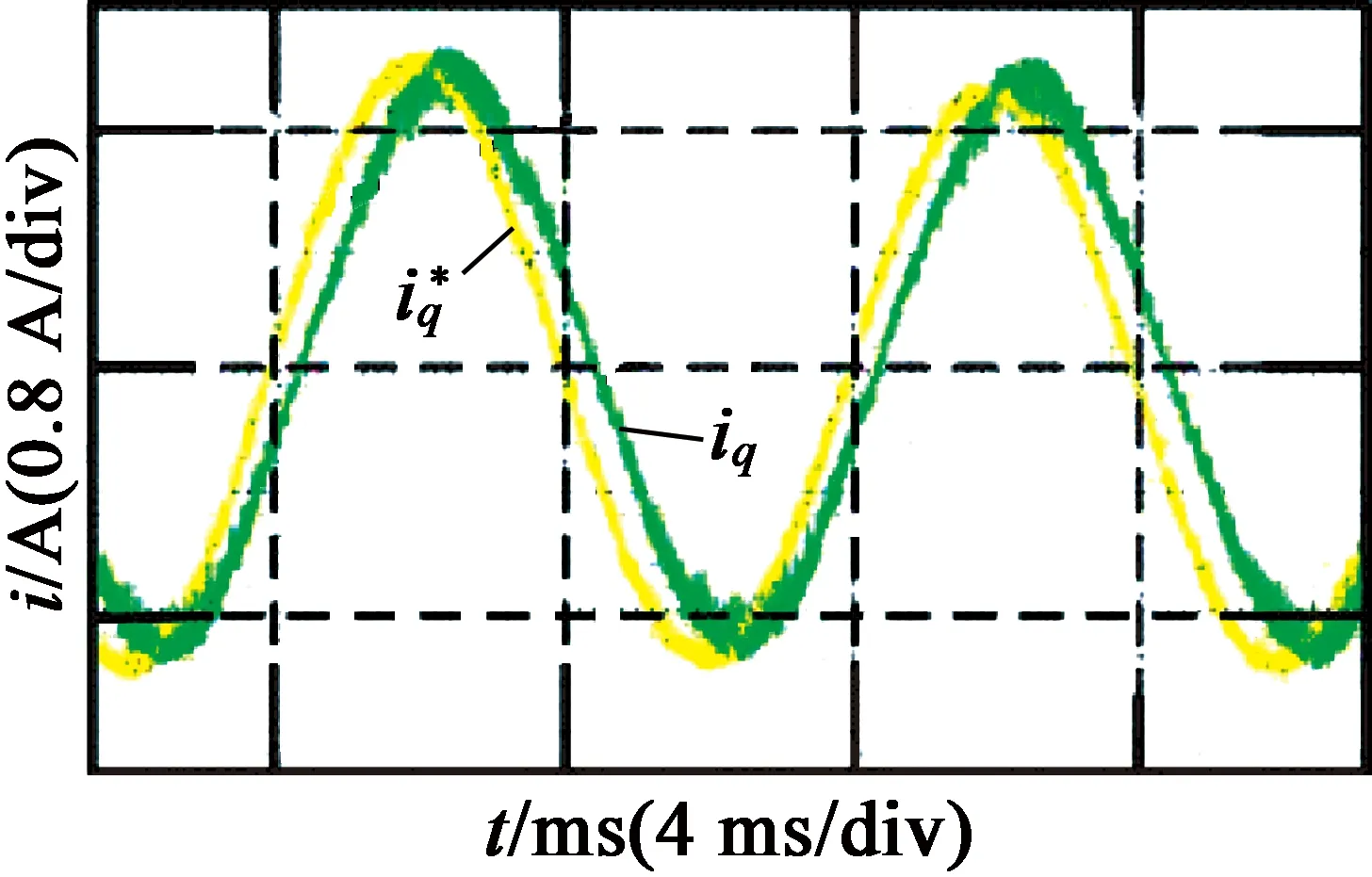
(b) 100 Hz

(c) 300 Hz

(d) 500 Hz

图12预测电流控制带宽测试实验结果

3 结 语

本文对比了三种电流控制方法，滞环电流控制方法简单、易于实现，且动态响应好、带宽较大，采样频率为20 kHz时的带宽基本可以达到500 Hz，但其精度差，一般无法满足精密控制系统的精度要求；同步旋转坐标系下的PI电流控制无静差，电流波动小，精度高，但其带宽较低，当开关频率为5 kHz时的带宽只有300 Hz左右，且传统的PI电流控制系统鲁棒性差；对于预测电流控制，传统预测电流控制存在时延和参数扰动的问题，通过估算下一时刻电压值可以解决时延问题，当参数匹配时，可以达到较好的控制效果，通过设计的滑模扰动观测器来补偿扰动电压可以解决参数扰动的问题，提高了系统的抗扰性，加入时延和扰动补偿后的预测电流控制系统精度较高，鲁棒性强，且带宽在开关频率为5 kHz时可以达到500 Hz左右，相较于前两者，具有较好的控制特性。